
- •1.Метод конечных элементов. Введение.
- •2.Область применения мкэ.
- •3. Основная идея метода конечных элементов
- •4. Последовательность процедур алгоритма мкэ при использовании принципа Лагранжа.
- •5.Преимущества мкэ.
- •6.Проблемы и недостатки мкэ
- •7. Дискретизация области : что это такое?
- •8.Типы конечных элементов.
- •9. Разбиение области на элементы
- •10. Как производится нумерация узлов
- •11. Матрица жесткости (мжэ) элемента.
- •12 Глобальная матрица жесткости всей области (мжс)
- •13. Как формируется глобальной матрицы жесткости всей области (мжс)
- •15.Системы линейных алгебраических уравнений и методы их решения
- •17.Решение систем линейных алгебраических уравнений прямым методом Гаусса.
- •18. Методы, используемые при решении систем линейных алгебраических уравнений
- •32. Матрица жесткости стержня в общей системе координат
- •33. Составление матрицы жесткости мжс для всей конструкции
- •35. Как правильно нумеровать стержни и узлы фермы?
- •36. Последовательность вычисления внутренних усилий в стержне.
- •40. Общая характеристика метода конечных элементов
- •41. Последовательность процедур общей схемы алгоритма мкэ
- •43. Достоинства и недостатки метода мкэ
- •44. Что такое дискретизация области?
- •45. Что такое матрица жесткости?
- •49.Одномерный конечный элемент
- •50. Двумерный конечный элемент
- •51. Трехмерный конечный элемент
- •52. Осесимметричный конечный элемент
9. Разбиение области на элементы
Процесс дискретизации может выть разделен на два этапа: разбиение тела на элементы и нумерация элементов и узлов. Последний этап логически совершенно прост, но усложняется в связи с нашим желанием повысить эффективность вычислений.
В этом разделе рассматривается разбиение двумерной области на линейные треугольные элементы. Двумерная область выбрана для удобства иллюстрации; кроме того, идеи, представленные здесь, могут быть обобщены на случай трехмерного тела. Дискретизация одномерного тела почти тривиальна, так как она сводится только к делению отрезка на более короткие участки.
Разбиение двумерного тела на треугольники выделено потому, что этот элемент — простейший из двумерных элементов в смысле аналитической формулировки. Требование простоты элемента связано с тем, что при моделировании области должно быть использовано большое число элементов, поэтому деление области на треугольники , вероятно, наилучший способ разбиения.
10. Как производится нумерация узлов
Нумерация узлов была бы тривиальной операцией, если бы номера узлов не влияли на эффективность вычислений, необходимых для получения решения. Использование метода конечных элементов приводит к системе линейных алгебраических уравнений, большое число коэффициентов которой равно нулю. Рассмотрение матрицы коэффициентов системы показывает, что все ненулевые коэффициенты и некоторые нулевые находятся между двумя линиями, параллельными главной диагонали (рис. 2.10). Расстояние между главной диагональю
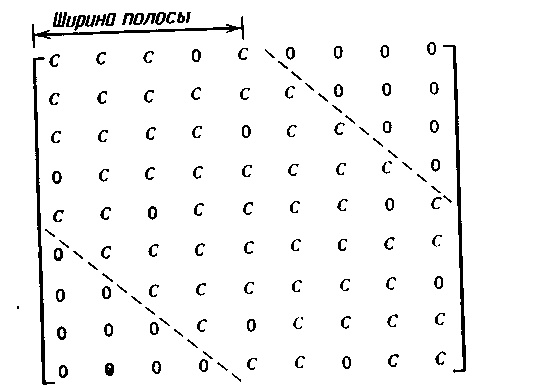
Рис. 2.10. Ширина полосы ненулевых элементов (коэффициентов) матрицы системы уравнений. (буквы С обозначает ненулевые коэффициенты.)
и этими линиями называется шириной полосы матрицы. Все коэффициенты вне этой полосы равны нулю, и они не должны сохраняться в машинной памяти. Правильная вычислительная программа использует только те коэффициенты матрицы, которые находятся внутри указанной полосы. Уменьшение ширины полосы приводит к сокращению размеров требуемой машинной памяти, а также к сокращению времени вычислений. Ширина полосы В вычисляется по формуле
B = ( R+1) Q (2.1)
 где
R
- максимальная по элементам величина
наибольшей разности между номерами
узлов в отдельном элементе, Q
- число неизвестных (число степеней
свободы) в каждом узле. Мини-мизация
величины В
связана
с минимизацией R,
что, в частности, может быть осуществлено
последовательной нумерацией узлов при
движении в направлении наименьшего
размера тела. Два разных способа
нумерации узлов в теле показаны на рис.
2.11, а
и
б.
Наибольшие
разности между номерами узлов для первых
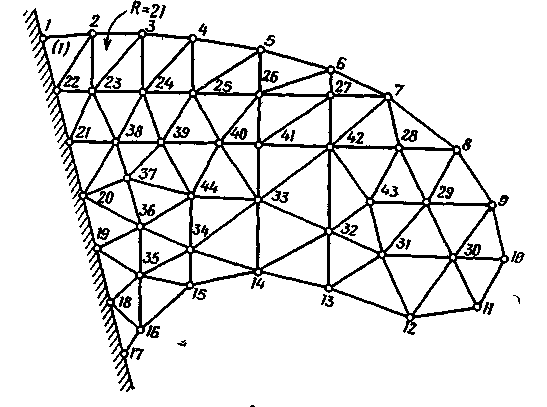
элементов на рис. 2.11, а и б
равны
7 и 21 соответственно. Значения R
для
полных наборов элементов равны 9 и 21.
Для ширины полосы получаются значения
10 и 22 , если в каждом узле отыскивается
по одной неизвестной величине ,
где
R
- максимальная по элементам величина
наибольшей разности между номерами
узлов в отдельном элементе, Q
- число неизвестных (число степеней
свободы) в каждом узле. Мини-мизация
величины В
связана
с минимизацией R,
что, в частности, может быть осуществлено
последовательной нумерацией узлов при
движении в направлении наименьшего
размера тела. Два разных способа
нумерации узлов в теле показаны на рис.
2.11, а
и
б.
Наибольшие
разности между номерами узлов для первых
элементов на рис. 2.11, а и б
равны
7 и 21 соответственно. Значения R
для
полных наборов элементов равны 9 и 21.
Для ширины полосы получаются значения
10 и 22 , если в каждом узле отыскивается
по одной неизвестной величине ,
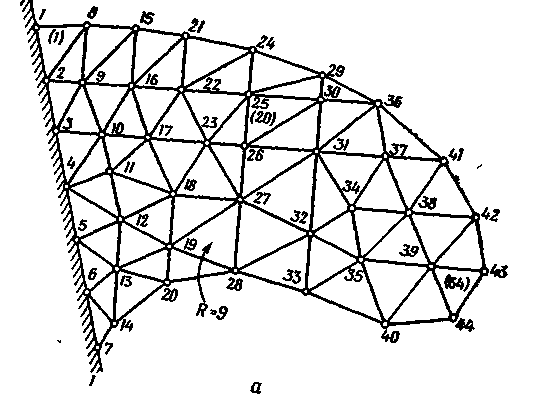
V
 б
б
Рис. 2.11. Два примера нумерации узлов при разбиении на элементы двумерного тела.
или значения 20 и 44, если в каждом узле рассматриваются две неизвестные величины. Правильная нумерация узлов в этом примере сокращает машинную память более чем на 50%.
Нумерация элементов представляет собой простую процедуру. Обычно принято номер элемента помещать в круг ( или заключать в круглые скобки) с тем, чтобы избежать путаницы с номерами узлов. Элемент (1) на рис. 2.11, а содержит узлы с номерами 1, 2 и 8. Нумерация элементов не влияет на вычислительные аспекты задачи.
