Труднорешаемые задачи и np-полнота. [8, 4 гл.34.]

Различные задачи и алгоритмы их решения имеют различную временную сложность, и выяснение того, какие алгоритмы «достаточно эффективны», а какие «совершенно неэффективны», всегда будет зависеть от конкретной ситуации. Но возникает вопрос: Когда нужно считать, что задача действительно труднорешаема? В теории принято эту границу проводить между полиномиальными и экспоненциальными алгоритмами.

Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность равна O(p(n)), где p(n) – некоторая полиномиальная функция. Алгоритмы, временная сложность которых не поддается подобной оценке, называют «экспоненциальными».

Различие между двумя указанными типами алгоритмов становятся особенно существенными при решении задач большого размера, и проявляются еще более убедительно, если проанализировать влияние увеличения быстродействия ЭВМ на время работы алгоритмов. Например, для T(n)=2ⁿ увеличение скорости вычислений в 10 раз приводит лишь к тому, что размер наибольшей задачи, разрешимой за один час, возрастет только (ориентировочно) на 3,3, в то время как для T(n)= этот размер возрастет почти в 3,16 раза (ориентировочно).

Эффект десятикратного ускорения при последующем увеличении скорости вычислений.

Большинство экспоненциальных алгоритмов – это просто варианты полного перебора, в то время как полиномиальные алгоритмы обычно можно построить лишь тогда, когда удается более глубоко проникнуть в суть решаемой задачи. Имеется широко распространенное соглашение, согласно которому задача не считается «хорошо решаемой» до тех пор, пока для неё не получен полиномиальный алгоритм. Поэтому задачу принято называть труднорешаемой, если для её решения не существует полиномиального алгоритма.

Здесь надо зафиксировать несколько уточнений:

• Временная сложность в этих рассуждениях разумеется как мера поведения алгоритма в худшем случае.

Уже отмечалось раньше, что даже экспоненциальный (в худшем случае) алгоритм может хорошо работать на практике, как например симплекс-метод для задач линейного программирования. Но подобные примеры очень редки, и, к сожалению, на сегодняшний день даже нет полноценных объяснений, почему эти алгоритмы успешно работают на практике... методы доказательства оценок для среднего времени работы тоже относятся к разряду очень сложных математических вопросов.

• Причиной труднорешаемости задачи может быть то обстоятельство, что искомое решение настолько велико, что не может быть выражено в виде представления, длина которого была бы ограничена полиномом от длины входа.

Например, в варианте задачи коммивояжера требуется найти все маршруты (требуемого вида) длины, не превосходящей В. Можно построить индивидуальную задачу о коммивояжере, в которой имеется экспоненциальное число требуемых маршрутов, поэтому не существует алгоритма с полиномиальной временной сложностью, который все их перечисляет.

Этот аспект труднорешаемости видимо естественнее трактовать как указание на то, что постановка не реалистична, поскольку запрошено больше информации, чем когда-либо сможем использовать. В связи с этим этот аспект труднорешаемости исключается из здесь обсуждаемых рассмотрений.

В связи с вышесказанным сделаем некоторые уточнения. Введем понятие абстрактной задачи: Определим абстрактную задачу (abstract problem) Q как бинарное отношение между множеством экземпляров (instances) задачи и множеством S решений (solutions). Например, экземпляр задачиКратчайший путь состоит из трех элементов: графа и двух вершин. Решением этой задачи является минимальная по длине последовательность ребер графа между заданными вершинами; при этом пустая последовательность понимается как отсутствие такого пути. Сама задача Кратчайший путь представляет собой отношение, сопоставляющее каждому экземпляру графа и двум его вершинам кратчайший путь по графу, соединяющий эти две вершины. Поскольку кратчайший путь может быть не единственным, конкретный экземпляр задачи может иметь несколько решений.

Поскольку как было заявлено выше, число решений может быть может быть достаточно велико, а нас интересует максимальная по всем экземплярам сложность решения, мы будем рассматривать только задачи распознавания (decision problems), т.е. задачи, которые имеют только два возможных ответа – «да» или «нет». Обычно для кандидатов в труднорешаемые задачи естественным образом формулируются соответствующие задачи распознавания, которые решаются не труднее, но остаются при этом кандидатами в труднорешаемые. Например, задачу распознавания Путь, соответствующую задаче Кратчайший путь, может быть сформулирована следующим образом: Пусть — экземпляр задачи принятия решенияПуть. Тогда равенство Путь(i) = 1 (да) выполняется, если количество ребер в кратчайшем пути из вершины в вершинуне превышает; в противном случаеПуть(i) = 0 (нет). Ограничившись задачами распознавания, мы избавимся в постановках задач от многообразных вариантов типа вышерассмотренного и сконцентрируем внимание на наиболее существенных аспектах труднорешаемости.

Многие абстрактные задачи являются не задачами принятия решения, а задачами оптимизации (optimization problems), в которых некоторое значение подлежит минимизации или максимизации. Однако обычно не составляет труда сформулировать задачу оптимизации как задачу принятия решения, которая не сложнее исходной.

Причины труднорешаемости задач достаточно сложно анализируемы. Зачастую незначительное изменение условия задачи переводит ее из одного класса в другой. Приведем примеры таких ситуаций:

Поиск самых коротких и самых длинных простых путей в графе. В дальнейшем мы убедимся, что поиск кратчайшего пути от некоторой вершины отдельно взятого источника в ориентированном графе G = ( V, Е) можно найти в течение времени O(VE). Однако поиск самого длинного пути между двумя вершинами оказывается сложным. Задача по определению того, содержит ли граф простой путь, количество ребер в котором не меньше заданного числа, является труднорешаемой.

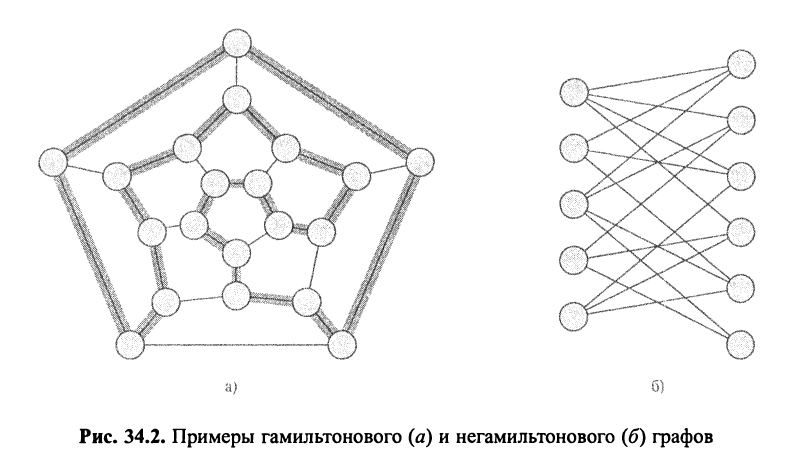
Эйлеров и Гамильтонов циклы. Эйлеров цикл (Euler tour) связанного ориентированного графа G = (У, Е) — это цикл, в котором переход по каждому ребру G осуществляется ровно один раз, хотя допускается неоднократное посещение некоторых вершин. Определить наличие Эйлерова цикла (а также найти составляющие его ребра) можно в течение времени О (Е). Гамильтонов цикл (hamiltonian cycle) ориентированного графа G = (V, Е) — это простой цикл, содержащий все вершины из множества V. Задача по определению того, содержится ли в ориентированном графе Гамильтонов цикл, является труднорешаемой.

2-CNF- и З- CNF-выполнимость. Булева формула содержит переменные, принимающие значения 0 и 1, булевы операторы, такие как & (И), V (ИЛИ) и (НЕ), а также скобки. Булева формула называется выполнимой (satisfiable), если входящим в ее состав переменным можно присвоить такие значения 0 и 1, чтобы в результате вычисления формулы получилось значение 1. Булева формула представлена в к-конъюнктивной нормальной форме (fc-conjunctive normal form), или fc-CNF, если она имеет вид конъюнкции (И) взятых в скобки выражений, являющихся дизъюнкцией (ИЛИ) ровно к переменных или их отрицаний (НЕ). Например, формулапредставлена в 2-CNF. (Для нее существует выполнимый набор) Можно сформулировать алгоритм с полиномиальным временем работы, позволяющий определить, является ли 2-CNF формула выполнимой. Однако, определение того, является ли 3-CNF формула выполнимой — это труднорешаемая задача задача.

Понятие труднорешаемой задачи оказывается, по существу, независимым и от способа кодирования задачи, и от модели детерминированного вычислителя, используемых при определении временной сложности. При определенных условиях можно доказать, что для различных схем кодирования и различных моделей вычислителя имеет место полиномиальная сводимость соответствующих алгоритмов решения задач (с помощью моделирования за полиномиальное время).

Рассмотрим задачу принятия решения, скажем, задачу А, которую хотелось бы решить в течение полиномиального времени. Назовем входные данные отдельно взятой задачи экземпляром этой задачи. Кроме того предположим, что существует другая задача принятия решения, скажем, В, для которой заранее известно, как решить ее в течение полиномиального времени. Наконец, предположим, что имеется процедура с приведенными ниже характеристиками, преобразующая любой экземпляр задачи А в некоторый экземплярзадачи В.

1. Это преобразование занимает полиномиальное время.

2. Ответы являются идентичными, т.е. в экземпляре ответ "да" выдается тогда и только тогда, когда в экземпляретоже выдается ответ "да".

Назовем такую процедуру алгоритмом сведения. Эта процедура предоставляет описанный ниже способ решения задачи А в течение полиномиального времени.

1. Заданный экземпляр задачи А с помощью алгоритма сведения с полиномиальным временем преобразуется в экземплярзадачи В.

2. Запускается алгоритм, решающий экземпляр задачи принятия решения задачи В в течение полиномиального времени.

3. Ответ для экземпляра используется в качестве ответа для экземпляра.

Поскольку для выполнения каждого из перечисленных выше этапов требуется полиномиальное время, это относится и ко всему процессу в целом, что дает способ решения экземпляра задачи в течение полиномиального времени. Другими словами, путем сведения задачи А к задаче В "простота" задачи В используется для доказательства "простоты" задачи А.

Первые результаты о труднорешаемости задач – классические результаты о неразрешимости. Но в данном контексте нас интересуют только разрешимые задачи. Поскольку все труднорешаемые задачи так или иначе связаны с перебором большого (часто экспоненциального) числа вариантов, то возникает вопрос: а можно ли найти решение задачи не перебирая всех её вариантов. Попытка построить модель вычислителя, который не учитывает время на перебор вариантов решения, приводит к понятию недетерминированного вычислителя.

Именно эта (недетерминированная) «нереалистичная» модель вычислителя играет важную роль в постановке проблемы об NP-полноте. В дальнейшем нас будут интересовать труднорешаемые задачи, для которых имеется полиномиальный алгоритм решения, но для недетерминированного вычислителя (для которого надо ещё определить понятие – время работы).

Классическая модель недетерминированного вычислителя - это недетерминированная машина Тьюринга. Для программистов видимо более удобной является модель недетерминированной RAM-машины или можно воспользоваться любым процедурным языком программирования – убрать всё лишнее (что загромождает рассуждения, но не дает ничего нового с учетом полиномиальной сводимости), но добавить:

• Оператор недетерминированного выбора: V ^boolean:=?

Этот оператор устанавливает значение логической переменной V , важный деликатный вопрос – как? Он может установить значение либо true, либо false, но не в вероятностном смысле, а в смысле альтернативных вариантов срабатывания. Можно рассмотреть вариант работы программы, когда при текущем выполнении он установит значение true, но можно рассмотреть альтернативный вариант работы программы, когда при текущем выполнении он установит значение false, и при каждом повторном выполнении он может альтернативно поступить независимо от предыдущих вариантов срабатывания.

• Оператор «успех» – приводит к успешному завершению работы программы.

• Оператор «неудача» – тоже приводит завершению работы программы, но неудачному.

Любой из альтернативных вариантов работы такого вычислителя на заданном входе, который завершается оператором «успех», будем называть принимающим вычислением (для этого входа). Такой алгоритм решает задачу распознавания в следующем смысле: для заданного входа отвечает на поставленный вопрос – «да», если имеется хотя бы одно принимающее вычисление для этого входа, и отвечает на поставленный вопрос – «нет», если для этого входа нет принимающих вычислений, т.е. в любом из альтернативных вариантов работы на этом входе алгоритм завершает работу оператором «неудача» либо даже бесконечно циклит. Время работы такого недетерминированного алгоритма на входе с ответом «да» – минимальное время по всем принимающим вычислениям, а на входе с ответом «нет» – считается единицей. Время работы (в худшем) на входах длины n – максимальное время работы по всем входам длины n. Заметим, что временная сложность такого алгоритма вычисляется только по принимающим вычислениям.

Алгоритмы, описанные в терминах недетерминированного вычислителя естественно трактовать как математическую формализацию интуитивного понятия переборный алгоритм. Специфические возможности оператора недетерминированного выбора с учетом специфики определений понятий «алгоритм решает задачу» и «время работы» такого алгоритма позволяют представить решение задачи распознавания в виде двух стадий - стадии угадывания и стадии проверки, смысл этих двух стадий поясним на примере.

Рассмотрим пример переборного решения задачи «Коммивояжер». В условии даны: множество городов, расстояния между ними и число В. Спрашивается: существует ли проходящий через все города маршрут длины, не превосходящей В. Полиномиальный детерминированный алгоритм решения этой задачи не известен, но можно предложить следующий полиномиальный недетерминированный алгоритм:

• Сначала на стадии угадывания с помощь недетерминированного выбора формируем (любой) маршрут (длины не более В). Отметим, проверка длины формируемого маршрута не приводит к существенным потерям времени.

• Потом можно проверить – обходит ли сформированный маршрут все города. Отметим, что такую проверку за полиномиальное время можно выполнить и детерминированным алгоритмом.

Не представляет труда на основе этой схемы предложить детерминированный (переборный) алгоритм, но поскольку количество перебираемых маршрутов экспоненциально, естественно мы получим экспоненциальный алгоритм.

Основное назначение «полиномиального недетерминированного алгоритма» состоит в объяснении понятия «проверяемости» за полиномиальное время», а не в том, чтобы служить реалистичным методом решения задач распознавания свойств. При каждом входе такой алгоритм имеет не одно, а несколько возможных вычислений - по одному для каждой возможной догадки.

Имеется еще одно важное отличие «решения» задачи распознавания недетерминированным алгоритмом от решения детерминированным алгоритмом, а именно в первом случае отсутствует симметрия между ответами «да» и «нет».

Если задача: «Дано I; верно ли, что для I выполняется свойство X?» может быть решена полиномиальным (детерминированным) алгоритмом, то такое же утверждение справедливо и для дополнительной задачи; "Дано I, верно ли, что для I не выполняется свойство X?». Это следует из того, что детерминированный алгоритм останавливается при всех входах, поэтому достаточно поменять местами ответы «да» и «нет».

Совершенно не очевидно, что то же самое верно для всех задач, разрешимых за полиномиальное время недетерминированными алгоритмами. Например, дополнение задачи «Коммивояжер»: дано множество городов, расстояния между ними и граница В; верно ли, что нет маршрута, проходящего через все города и имеющего длину, не превосходящую В? Для выяснения, имеет ли поставленный вопрос ответ «да», не известен способ, который был бы короче, чем проверка всех (или почти всех) возможных маршрутов. Несмотря на интенсивные исследования в этой области, никому не удалось установить, замкнут ли класс NP относительно операции дополнения. Другими словами, следует ли из соотношения соотношение ? Можно определить класс сложности co-NP (complexity class co-NP) как множество языков L, для которых выполняется соотношение . Вопрос о том, замкнут ли класс NP относительно дополнения, можно перефразировать как вопрос о соблюдении равенства NP = coNP. Поскольку класс Р замкнут относительно дополнения, отсюда следует, что . Однако, опять же не известно, выполняется ли равенство , т.е. существует ли хоть один язык в множестве .

На рис. представлены четыре возможные ситуации. На каждой диаграмме одна область, содержащая другую, указывает, что внутренняя область является собственным подмножеством внешней. В части а) рисунка показана ситуация, соответствующая равенству Р = NP = co-NP.

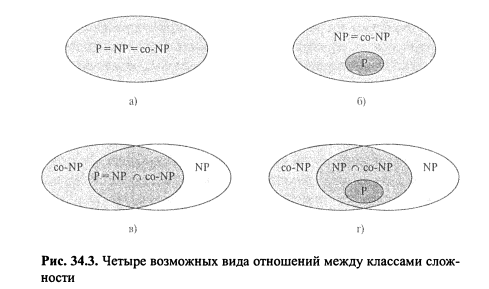
Большинство исследователей считает этот сценарий наименее вероятным. В части б) показано, что если класс NP замкнут относительно дополнения (NP=coNP), не обязательно справедливо равенство Р = NP. В части в изображена ситуация, когда Р = NP co-NP, но класс NP не замкнут относительно дополнения. И наконец, в части г выполняются соотношения NP co-NP и Р NP co-NP. Большинство исследователей считают эту ситуацию наиболее вероятной.

Класс P (полиномиальных задач распознавания) – множество задач распознавания, для которых существует полиномиальный детерминированный алгоритм решения.

Класс NP (недетерминировано полиномиальных задач распознавания) – множество задач распознавания, для которых существует полиномиальный недетерминированный алгоритм решения.

Очевидно включение P  NP, поскольку детерминированный алгоритм по определению является недетерминированным. Но есть много причин считать это включение строгим. Полиномиальные недетерминированные алгоритмы определенно оказываются более мощными, чем полиномиальные детерминированные, и не известны общие методы их превращения в детерминированные полиномиальные.

Если P не совпадает с NP, то различие между P и NP-P очень существенно. Все задачи из P могут быть решены (детерминированными) полиномиальными алгоритмами, а все задачи из NP-P труднорешаемы, и математическим уточнением понятия переборная задача распознавания служит задача из NP-P.

В исследованиях проблемы PNP важное положение занимает понятие полиномиальная сводимость, используя ранее введенное понятие (и обозначение) сводимости - задача A полиномиально сводима к задаче B , если A _p(n)B для некоторого полинома p(n). Задача A называется NP-полной, если A  NP и для любой другой задачи B  NP имеет место полиномиальная сводимость B к A.

Честь быть «первой» NP-полной задачей выпала на долю задачи распознавания выполнимости формул булевой логики. Рассмотрим язык L, образованный всеми цепочками, представляющими выполнимые булевы формулы (т. е. формулы, принимающие значение 1 на некотором наборе 0-1-значений переменных). Мы утверждаем, что L принадлежит NP . Недетерминированный алгоритм, распознающий L, начинает с того, что "угадывает" выполняющий набор 0-1-значений пропозициональных переменных во входной цепочке, если такой набор существует. Затем угаданное значение 0 или 1 каждой переменной подставляется вместо всех вхождений этой переменной во входную цепочку. Далее вычисляется значение полученного выражения, чтобы проверить его совпадение с 1. Это вычисление осуществляется за время, пропорциональное длине выражения, многими алгоритмами синтаксического анализа. Но даже и без них не трудно вычислить значение булевой формулы за шагов.Следовательно, некоторая недетерминированная машина Тьюринга допускает выполнимые булевы формулы с полиномиальной временной сложностью, и потому задача распознавания выполнимости булевых формул принадлежит NP. Снова отметим, что недетерминизм пригодился, чтобы "параллелизовать" задачу, поскольку "угадывание" правильного решения в действительности означает параллельную проверку всех возможных решений.

Кук С.А. показал как формулами булевой логики можно описать работу любой программы недетерминированного вычислителя и на этой основе доказал полиномиальную сводимость любой NP-задачи к задаче о выполнимости.

Таким образом, важную роль в доказательстве NP полноты играет сведение. Если вспомнить, что при доказательстве NP-полноты требуется показать, насколько сложной является задача, а не насколько она простая, доказательство NP- полноты с помощью сведения с полиномиальным временем работы выполняется обратно описанному выше способу. Продвинемся в разработке этой идеи еще на шаг и посмотрим, как с помощью сведения с полиномиальным временем показать, что для конкретной задачи В не существует алгоритмов с полиномиальным временем работы. Предположим, что имеется задача принятия решения А, относительно которой заранее известно, что для нее не существует алгоритма с полиномиальным временем работы. Предположим также, что имеется преобразование, позволяющее в течение полиномиального времени преобразовать экземпляры задачи А в экземпляры задачи В. Теперь с помощью простого доказательства "от противного" можно показать, что для решения задачи В не существует алгоритмов с полиномиальным временем работы. Предположим обратное, т.е. что существует решение задачи В в виде алгоритма с полиномиальным временем работы. Тогда, воспользовавшись методом сведения можно получить способ решения задачи А в течение полиномиального времени, а это противоречит предположению о том, что таких алгоритмов для задачи А не существует.

Если речь идет о NP-полноте, то здесь нельзя предположить, что для задачи А вообще не существует алгоритмов с полиномиальным временем работы. Однако методология аналогична в том отношении, что доказательство NP-полноты задачи В основывается на предположении о NP-полноте задачи А.

Методом (полиномиального) сведения на сегодняшний день доказана NP-полнота обширнейшего семейства задач в различных областях: в булевой логике, в теории графов, в арифметике, при разработке сетей, в теории множеств и разбиений, при хранении и поиске информации, при планировании вычислительных процессов, в математическом программировании, в алгебре и теории чисел, при создании игр и головоломок, в теории автоматов и языков, при оптимизации программ, в биологии, в химии, физике и т.п.

k-кликой в графе G называют k-узельный полный подграф (каждая пара различных узлов в этом подграфе соединена ребром) графа G. Задача о клике формулируется так: содержит ли данный граф G -клику, где k — данное целое число?

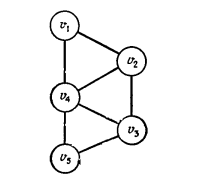
Пример задачи о клике для графа G на рис. при k=3 можно закодировать цепочкой

3 (1,2) (1,4) (2,3) (2,4) (3,4) (3,5) (4, 5). Первое число представляет значение k. За ним идут пары узлов, соединенных ребрами, причем узел представлен числом i. Таким образом, ребра в порядке перечисления выглядят так:.

Задача о клике принадлежит классу NP. Недетерминированная машина Тьюринга сначала может "догадаться", какие k узлов составляют полный подграф, а затем проверить, что любая пара этих узлов соединена ребром, при этом для проверки достаточно шагов, где— длина кода задачи о клике.

Для изучения важных NP-полных задач, касающихся неориентированных графов, нам понадобятся следующие определения.

Определения. Пусть G=(V, Е) — неориентированный граф.

1. Узельным покрытием графа G называется такое подмножество , что каждое ребро графаG инцидентно некоторому узлу из S.

2. Гамильтоновым циклом называется цикл в графе G, содержащий все узлы из V.

3. Граф G называется k-раскрашиваемым, если существует такое приписывание целых чисел 1, 2,. . ., k, называемых цветами, узлам графа G, что никаким двум смежным узлам не приписан один и тот же цвет. Хроматическим числом графа G называется такое наименьшее число k, что граф G -раскрашиваем.

Для представления важных NP-полных задач об ориентированных графах нам понадобятся следующие определения.

Определения. Пусть G—(V, Е) — ориентированный граф.

1. Множеством узлов, разрезающих циклы, называется такое подмножество , что каждый цикл вG содержит узел из S.

2. Множеством ребер, разрезающих циклы, называется такое подмножество , что каждый цикл вG содержит ребро из F.

3. Ориентированным гамильтоновым циклом называется цикл в ориентированном графе G, содержащий все узлы из V.

Теорема 10.2. Следующие задачи принадлежат классу NP

1. (Выполнимость) Выполнима ли данная булева формула?

2. (Клика) Содержит ли данный неориентированный граф k- клику?

3. (Узельное покрытие) Имеет ли данный неориентированный граф узельное покрытие размера k?

4. (Гамильтонов цикл) Имеет ли данный неориентированный граф гамильтонов цикл?

5. (Раскрашиваемость) Является ли данный неориентированный граф k-раскрашиваемым?

6. (Множество узлов, разрезающих циклы) Имеет ли данный ориентированный граф k-элементное множество узлов, разрезающих циклы?

7. (Множество ребер, разрезающих циклы) Имеет ли данный ориентированный граф k-элементное множество ребер, разрезающих циклы?

8. (Ориентированный гамильтонов цикл) Имеет ли данный ориентированный граф ориентированный гамильтонов цикл?

9. (Покрытие множествами) Существует ли для данного семейства множеств такое подсемейство изk множеств , что

10. (Точное покрытие) Существует ли для данного семейства множеств подсемейство попарно непересекающихся множеств, являющееся покрытием?

Теорема . Задача о клике полиномиально трансформируема в задачу об узельном покрытии. Поэтому задача об узельном покрытии NP-полна.

Доказательство. Пусть дан неориентированный граф G - (V, E). Рассмотрим его дополнение , где. Множествоявляется кликой вG тогда и только тогда, когда V\S является узельным покрытием графа . Действительно, еслиS — клика в G, то никакое ребро в не соединяет никакие два узла вS. Поэтому всякое ребро в инцидентно по меньшей мере одному узлу изV\S, откуда следует, что V\S есть узельное покрытие графа G. Аналогично, если V\S есть узельное покрытие графа , то каждое ребро изинцидентно по меньшей мере одному узлу изV\S. Поэтому никакое ребро из не соединяет два узла изS. Следовательно, каждая пара узлов из S соединена в G, и, значит, S — клика в G.

Чтобы узнать, существует ли -клика, построим графи выясним, содержит ли он узельное покрытие размера ||V||—k. Разумеется, поданному стандартному представлению графа G=(V, E) и числа k можно найти представление графа и числа ||V||—k за время, полиномиально зависящее от длины представления G и k.

Оригинальные идеи Кука оказались удивительно плодотворными. Они позволили свести много разнообразных вопросов о сложности в единый вопрос: «Верно ли, что NP-полные задачи труднорешаемы?»