1. Линейные структуры данных.

Для представления последовательностей используются массивы и линейные связные списковые структуры данных (с указателями). Используются также и смешанные способы представления на основе этих структур данных. Например, последовательность сложных (объемных) элементов может быть представлена вектором указателей на её элементы. Различные способы представления имеют различные сложностные характеристики по памяти и времени (в частности разные для разных операций) и могут оказаться более или менее приемлемыми в различных ситуациях.

Список базовых операций для (различного вида) последовательностей ¹⁷ [13 п.5.3.]:

• size(): возвращает количество элементов в последовательности.

• isEmpty(): возвращает логическое значение, подтверждающее, что последовательность пуста.

• atRank(r): возвращает позицию элемента с номером r.

• rankOf(р): возвращает номер элемента в позиции р.

• first(), last(): возвращает позицию «первого, последнего» элемента последовательности.

• before(р), after(р): возвращает позицию элемента последовательности, который «предшествует элементу, следует за элементом» позиции р.

• elemAtRank(r): возвращает элемент последовательности с номером r.

• replaceAtRank(r,e): замещает элемент с номером r на е и возвращает замещаемый.

• replaceElement(р,e): замещает элемент в позиции р на е и возвращает замещаемый.

• insertAtRank(r,e): добавляет новый элемент e в качестве r-го элемента последовательности.

• insertFirst(e): вставляет новый элемент е в качестве первого элемента в последовательности.

• insertLast(e): вставляет новый элемент е в качестве последнего элемента в последовательности.

• insertBefore(р,e): вставляет новый элемент е перед позицией p последовательности.

• insertAfter(р,e): вставляет новый элемент е после позиции p последовательности.

• remove(р): удаляет из последовательности элемент в позиции р.

• removeAtRank(r): удаляет из последовательности элемент с номером r.

Для варианта с последовательным доступом к компонентам аргумент «позиция» (номер) становится не нужным, все операции привязываются к текущей позиции.

Пусть —линейная последовательность изэлементов. Каждый элементпоследовательностиимеет уникальный индекс, выраженный целым числом в интервале [0,— 1], равный числу элементов, предшествующих. Таким образом, определим, что номер элементапоследовательностиравен количеству элементов, находящихся перед, то есть номер первого элемента последовательности равен 0, а последнего —— 1. Данный метод соответствует принципу индексирования массивов в Java и других языках программирования (в том числе С и C++). В определении не требуется, чтобы реализованная в массиве последовательность сохраняла элемент с номером 0 в ячейке с индексом 0, хотя это один из возможных вариантов. Понятие номера позволяет обращаться к «индексу» элемента последовательности без учета конкретной реализации списка. Итак, если элемент является r-ным элементом последовательности, его разряд равен г— 1. Таким образом, если номер элемента равен r, то номер предыдущего элемента (если он существует) равен r — 1, а следующего элемента (если он существует) — r+ 1. Следует, однако, отметить, что номер элемента может изменяться при обновлении последовательности. Например, при добавлении нового элемента в начале последовательности номер каждого элемента увеличится на 1. Линейная последовательность элементов, в которой доступ к элементам осуществляется по их номеру, называется вектором. Номер является простым и в то же время удобным средством, так как с его помощью определяется место добавления нового элемента или удаления элемента вектора.

Отметим, что массив – фактически статическая структура данных, а потому требует предварительного резервирования памяти, в то время как предварительная оценка максимального размера обрабатываемой последовательности для решаемой задачи может оказаться затруднительной. Кольцевой массив (circular array) – структура данных, основанная на техническом приеме, когда конец вектора как бы подклеивается к его началу. Последовательность хранится в таком векторе, начиная с некоторого (вообще говоря) промежуточного индекса в порядке возрастания индекса (с перескоком к нулевому на правой границе). Такой прием используется, когда операции добавления-удаления допускаются с обоих (или разных) концов последовательности, например в реализации очередей. Он позволяет повторно использовать освобождающийся сегмент вектора и при этом устранить необходимость сдвига элементов последовательности.

Вектор является абстрактным типом данных (АТД), который поддерживает следующие основные методы:

• elemAtRank(r): возвращает элемент последовательности с номером r.

• replaceAtRank(r,s): замещает элемент с номером r на s и возвращает замещаемый.

• insertAtRank(r,s): добавляет новый элемент s в качестве r-го элемента последовательности

• removeAtRank(r): удаляет из последовательности элемент с номером r.

Основной недостаток реализации вектора на основе простого массива состоит в необходимости предварительного указания размера массива, то есть максимального числа элементов вектора. Если же действительное число элементов значительно меньше N, то при такой реализации бесполезно занимается место в памяти. Хуже того, если окажется больше значения N, то реализация приведет к сбою программы. К счастью, существует простой способ разрешения этой проблемы.

Предположим, имеются средства увеличения размера массива А, содержащего элементы вектора S. Безусловно, в Java (и других языках программирования) в действительности невозможно увеличить размер массива, его длина ограничена заданным значением , как отмечалось ранее. Вместо этого при возникновении переполнения, то есть при,

и вызове метода insertAtRank выполняются следующие операции:

1) создается новый массив длиной;

2) копируется A[i] в B[i], где / = 0, ..., N- 1;

3) присваивается А = В, то есть используется В как массив, содержащий S.

Данная стратегия замещения массивов известна как расширяемый массив, так как она как бы продолжает исходный массив для размещения.

C точки зрения эффективности приведенная стратегия замещения массивов кажется относительно медленной, так как для замещения одного массива при необходимости вставки элемента требуется O{n) времени, что не очень приемлемо. Тем не менее, следует отметить, что после замещения массива появляется возможность добавления новых элементов перед необходимостью нового замещения. В результате можно показать, что время выполнения операций, производимых над изначально пустым вектором, в действительности не так уж велико. Для краткости назовем добавление последнего элемента вектора операцией «проталкивания». Далее, используя модель проектирования, называемую амортизацией, покажем, что последовательность подобных операций над вектором, реализованным на основе расширяемого массива, может быть достаточно эффективной.

Утверждение 5.1. Пусть S— вектор, реализованный на основе расширяемого массива А, как было описано выше. Общее время выполнения последовательности п операций проталкивания в массиве S при условии, что S изначально пустой, а А имеет размер N= n, есть O(n).

Для доступа к месту расположения элемента в списке может применяться не только понятие разряда. Если имеется список S, реализованный на основе однонаправленного или двусвязного списка, более удобным и эффективным является использование для определения места доступа и обновления списка узлов вместо разрядов. Рассмотрим абстрактное понятие узла, описывающего определенное «место» в списке, не вдаваясь в детали реализации списка.

Пусть S— линейный список, реализованный с помощью двусвязного списка. Простейшей его реализацией будет структура последовательно связанных компонент, изображенная на рис.

Каждая компонента в этой структуре состоит из двух ячеек памяти. Первая ячейка содержит сам элемент, вторая — указатель следующего элемента. Это можно реализовать в виде двух массивов, которые названы ИМЯ и СЛЕДУЮЩАЯ.

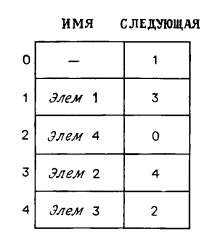
Если КОМПОНЕНТА — индекс в рассматриваемом массиве, то ИМЯ [КОМПОНЕНТА] — сам элемент, хранящийся там, а СЛЕДУЮЩАЯ [КОМПОНЕНТА]— индекс следующего элемента в списке (если такой элемент существует). Если КОМПОНЕНТА — индекс последнего элемента в этом списке, то СЛЕДУЮЩАЯ[КОМПОНЕНТА]=0.

procedure ВСТАВИТЬЭЛЕМЕНТ(СВОБОДНАЯ, ПОЗИЦИЯ):

begin

ИМЯ[СВОБОДНАЯ] ЭЛЕМЕНТ;

СЛЕДУЮЩАЯ[СВОБОДНАЯ] СЛЕДУЮЩАЯ[ПОЗИЦИЯ];

СЛЕДУЮЩАЯ [ПОЗИЦИЯ] СВОБОДНАЯ

end

Очевидным образом, время выполнения операции вставки не зависит от длины списка.

Часто в один и тот же массив вкладываются несколько списков. Обычно один из этих списков состоит из незанятых ячеек (будем называть его свободным списком). Для добавления элемента к списку А можно так изменить процедуру ВСТАВИТЬ, чтобы незанятая ячейка получалась путем удаления первой ячейки в свободном списке. При удалении элемента из списка А соответствующая ячейка возвращается в свободный список для будущего употребления.

Реализация связным списком позволяет выделять память динамически (в периоде выполнения) - столько и тогда, сколько и когда действительно требуется. Двусвязный список используется, когда необходим равноправный доступ, как к следующему, так и предшествующему элементам последовательности.

Операции	Массив (кольцевой)	Список (двусвязный)
size, isEmpty	0(1)	0(1)
atRank, rankOf, elemAtRank	0(1)	0(n)
first, last, before, after	0(1)	0(1)
replaceElement	0(1)	0(1)
replaceAtRank	0(1)	0(n)
insertAtRank, removeAtRank	0(n)	0(n)
insertFirst, insertLast	0(1)	0(1)
insertAfter, insertBefore	0(n)	0(1)
Remove	0(n)	0(1)

Еще две основные операции над списками — конкатенация (сцепление) двух списков, в результате которой образуется единственный список, и обратная к ней операция расцепления списка, стоящего после некоторого элемента, результатом которой будут два списка. Конкатенацию можно выполнить за ограниченное (постоянной величиной) число шагов, включив в представление списка еще один указатель. Этот указатель дает индекс последней компоненты списка и тем самым позволяет обойтись без просмотра всего списка для определения его последнего элемента. Расцепление можно сделать за ограниченное (постоянной величиной) время, если известен индекс компоненты, непосредственно предшествующей месту расцепления.

Списки можно сделать проходимыми в обоих направлениях, если добавить еще один массив, называемый ПРЕДЫДУЩАЯ. Значение ПРЕДЫДУЩАЯ[i] равно ячейке, в которой помещается тот элемент списка, который стоит непосредственно перед элементом из ячейки. Список такого рода называется дважды связанным. Из дважды связанного списка можно удалить элемент или вставить в него элемент, не зная ячейку, где находится предыдущий элемент.

В определенном смысле близким к понятию последовательность является понятие «Разреженный массив» (Sparse Array) – массив в котором ненулевые элементы составляют лишь малую долю от общего числа элементов. Такие вектора и матрицы часто встречаются в практических задачах линейной алгебры. С одной стороны, с концептуальной точки зрения – это статические типы (и структуры) данных с классическим набором операций линейной алгебры. Но с другой стороны, количество (и места) нулей в таком векторе может изменяться – его можно трактовать как последовательность ненулевых элементов с индексом в качестве позиции элемента.

Интересный и во многих отношениях полезный пример рассмотрен в классическом энциклопедическом труде «Искусство программирования» Кнут Д.Э. [14], задача «Осевое преобразование разреженной матрицы» т.1. п.2.2.6. «Массивы и ортогональные списки». В алгоритме решения этой задачи используется ортогонально (по строкам и столбцам) связное представление для разреженной матрицы, которое можно определить как базовый класс «Ортогональные списки» с парой индексов в качестве позиции элемента и операциями, аналогичными приведенным для последовательностей. А наследованием можно определить класс для разреженных матриц с классическим набором операций линейной алгебры.

Отметим другой вариант трактовки разреженных массивов – как разновидность АТД Словарь с парой индексов в качестве ключа элемента.

Линейные структуры данных, массивы и линейные связные списковые структуры (с указателями), используются и для представления множеств (и наборов).

Со списком часто работают очень ограниченными приемами. Например, элементы добавляются или удаляются только на конце списка. Иными словами, элементы вставляются и удаляются по принципу "последний вошел — первый вышел". В этом случае список называют стеком или магазином.

Часто стек реализуется в виде одного массива. Например, список

Элем 1, Элем 2, Элем 3

можно было бы хранить в массиве ИМЯ, как показано на рисунке

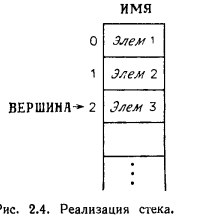
Переменная ВЕРШИНА является указателем последнего элемента, добавленного к стеку. Чтобы добавить (ЗАТОЛКНУТЬ) новый элемент в стек, значение ВЕРШИНА увеличивают на 1, а затем помещают новый элемент в ИМЯ1ВЕРШИНА]. (Поскольку массив ИМЯ имеет конечную длину , перед попыткой вставить новый элемент следует проверить, что ВЕРШИНА <) Чтобы удалить (ВЫТОЛКНУТЬ) элемент из вершины стека, надо просто уменьшить значение ВЕРШИНА на 1. Заметим, что не обязательно физически стирать элемент, удаляемый из стека. Чтобы узнать, пуст ли стек, достаточно проверить, не имеет ли ВЕРШИНА значение, меньшее нуля. Понятно, что время выполнения операций ЗАТОЛКНУТЬ и ВЫТОЛКНУТЬ и проверка пустоты не зависят от числа элементов в стеке.

Другой специальный вид списка — очередь, т. е. список, в который элементы всегда добавляются с одного (переднего) конца, а удаляются с другого. Как и стек, очередь можно реализовать одним массивом, как показано на рис. 2.5, где приведена очередь, содержащая список из элементов Р, Q, R, S, Т.

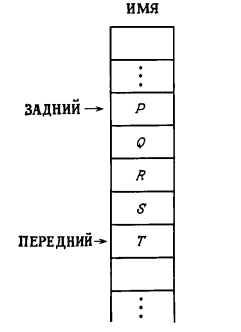
Реализация очереди в виде одного массива

Два указателя обозначают ячейки текущего переднего и заднего концов очереди. Чтобы добавить (ВПИСАТЬ) новый элемент к очереди, как и в случае стека, полагают ПЕРЕДНИЙ = ПЕРЕДНИЙ +1 и помещают новый элемент в ИМЯ1ПЕРЕДНИЙ]. Чтобы удалить (ВЫПИСАТЬ) элемент из очереди, заменяют ЗАДНИЙ на ЗАДНИЙ +1. Заметьте, что эта техника с точки зрения доступа к элементам основана на принципе "первый вошел — первый вышел".

Поскольку массив ИМЯ имеет конечную длину, скажем , указатели ПЕРЕДНИЙ и ЗАДНИЙ рано или поздно доберутся до его конца. Если длина списка, представленного этой очередью, никогда не превосходит, то можно трактовать ИМЯ[0] как элемент, следующий за элементом ИМЯ[n-1].

Элементы, расположенные в виде списка, сами могут быть сложными структурами. Работая, например, со списком массивов, мы на самом деле не добавляем и не удаляем массивы, ибо каждое добавление или удаление потребовало бы времени, пропорционального размеру массива. Вместо этого мы добавляем или удаляем указатели массивов. Таким образом, сложную структуру можно добавить или удалить за фиксированное время, не зависящее от ее размера.

Представления множеств

Обычно списки применяются для представления множеств. При этом объем памяти, необходимый для представления множества, пропорционален числу его элементов. Время, требуемое для выполнения операции над множествами, зависит от природы операции. Например, пусть А и В — два множества. Операция требует времени, по крайней мере пропорционального сумме размеров этих множеств, поскольку как список, представляющий А, так и список, представляющий В, надо просмотреть хотя бы один раз.

Подобным же образом операция требует времени, пропорционального сумме размеров множеств, поскольку надо выделить элементы, входящие в оба множества, и вычеркнуть один экземпляр каждого такого элемента. Если жеине пересекаются, можно найтиза время, не зависящее от размераи. Для этого достаточно сделать конкатенацию списков. Задача объединения двух непересекающихся множеств усложняется, если необходимо быстро определять, входит ли данный элемент в данное множество.

Другой способ представления множества, отличный от представления его в виде списка,— представление в виде двоичного (битового) вектора. Пусть U — универсальное множество (т. е. все рассматриваемые множества являются его подмножествами), состоящее из элементов. Линейно упорядочим его. Подмножествопредставляется в виде вектораизбитов, такого, чтоt-й разряд в равен 1 тогда и только тогда, когдаi-й элемент множества принадлежитS. Будем называть характеристическим вектором дляS.

Для представления множеств посредством характеристических 0-1-векторов необходимо иметь оценку мощности универсального множества (т.к. массив – статическая структура данных) и установить взаимно однозначное соответствие¹⁸ между элементами универсального множества и областью допустимых значений индексов массива-вектора. При таком представлении базовые операции для множеств реализуются с хорошими характеристиками по времени, но по памяти оно может оказаться расточительным, если универсальное множество очень большое, а используемые его подмножества относительно очень маленькие (получаем случай очень разреженного массива). Для реализации теоретико-множественных операций (, , разность) потребуется полный просмотр такого вектора (размером, равным мощности универсального множества).

Представление множеств линейными связными списками устраняет ограничения, свойственные статическим структурам данных, но при этом теряются возможности эффективного прямого доступа по индексу – операция Принадлежать (Найти элемент) реализуема только просмотром списка.

Аналогичные характеристики для представления упорядоченных множеств массивами и линейными связными списками, причем появляются проблемы поддержания отношения порядка и соответствующие варианты решения этих проблем.

Для представления более сложных АТД используются более сложно организованные структуры данных.

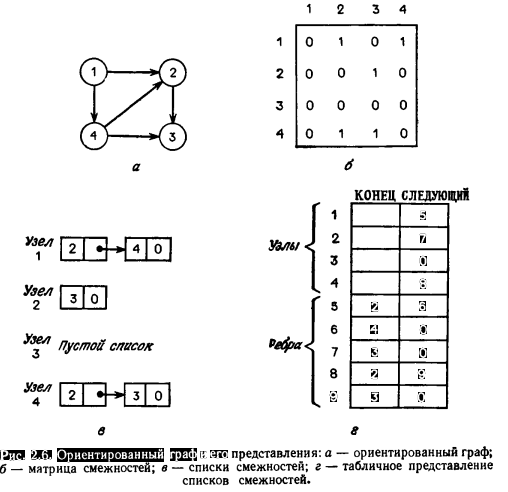
2. Графы

Известно несколько представлений графа G=(V, E). Один из них — матрица смежностей, т.е. матрица А размера ||V||x||V||, состоящая из 0 и 1, в которой =1 тогда и только тогда, когда есть ребро из узла i в узел у. Представление в виде матрицы смежностей удобно для тех алгоритмов на графах, которым часто нужно знать, есть ли в графе данное ребро, ибо время, необходимое для определения наличия ребра, фиксировано и не зависит от ||V|| и \\E\\. Основной недостаток применения матрицы смежностей заключается в том, что она занимает память объемадаже тогда, когда граф содержит толькоребер. Уже начальное заполнение матрицы смежностей посредством "естественной" процедуры требует времени, что сводит на нет алгоритмы сложностипри работе с графами, содержащими лишьребер. Хотя разработаны методы для преодоления этой трудности, почти неизбежно возникают другие проблемы, которые приводят к тому, что алгоритмы сложности О(||V||), основанные на работе с матрицей смежностей, встречаются редко. Интересной альтернативой является представление строк и (или) столбцов матрицы смежностей в виде двоичных векторов. Такое представление может способствовать значительной эффективности алгоритмов на графах.

Еще одно возможное представление графа — с помощью списков. Списком смежностей для узла v называется список всех узлов w, смежных с v. Граф можно представить с помощью списков смежностей, по одному для каждого узла.