Деревья.
Также как и для последовательностей, доступ к компонентам (вершинам) дерева может быть определен как прямой или последовательный. Будем различать понятия: позиция вершины дерева - однозначно идентифицирующая вершину и её положение в дереве, и элемент – информация, ассоциированная с вершиной дерева (в частности, просто хранимая вместе с ней).
Определение. Ориентированный граф без циклов называется ориентированным ациклическим графом. (Ориентированное) дерево (иногда его называют корневым деревом) — это ориентированный ациклический граф, удовлетворяющий следующим условиям:
1) имеется в точности один узел, называемый корнем, в который не входит ни одно ребро,
2) в каждый узел, кроме корня, входит ровно одно ребро,
3) из корня к каждому узлу идет путь (который, как легко показать, единствен).
Ориентированный граф, состоящий из нескольких деревьев, называется лесом. Леса и деревья — столь часто встречающиеся частные случаи ориентированных ациклических графов, что для описания их свойств стоит ввести специальную терминологию.
Определение.
Пусть F=(V, E) — граф, являющийся лесом.
Если
принадлежит Е, то
называется
отцом узла
,
a
— сыном узла
.
Если есть путь из
в
,
то
называется предком узла
,
a
— потомком узла
.
Более того, если
,
то
называется подлинным предком узла
,
a
—
подлинным потомком узла
.
Узел без подлинных потомков называется
листом. Узел
и его потомки вместе образуют поддерево
леса F, и узел
называется корнем этого поддерева.
Глубина узла v в дереве — это длина пути из корня в v. Высота узла v в дереве — это длина самого длинного пути из v в какой-нибудь лист. Высотой дерева называется высота его корня. Уровень узла v в дереве равен разности высоты дерева и глубины узла v.
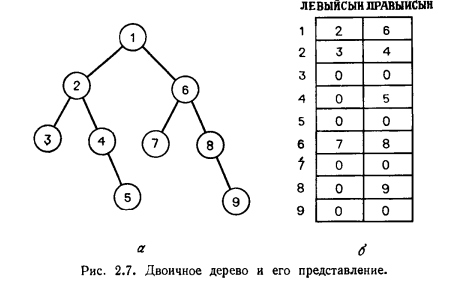
Например, на рис. 2.7,а узел 3 имеет глубину 2, высоту 0 и уровень 1. Упорядоченным деревом называется дерево, в котором множество сыновей каждого узла упорядочено. При изображении упорядоченного дерева мы будем считать, что множество сыновей каждого узла упорядочено слева направо. Двоичным (бинарным) деревом называется такое упорядоченное дерево, что
1) каждый сын произвольного узла идентифицируется либо как левый сын, либо как правый сын,
2) каждый узел имеет не более одного левого сына и не более одного правого сына.
Поддерево
,
корнем которого является левый сын узла
v (если такое существует), называется
левым поддеревом узла v. Аналогично
поддерево
корнем которого является правый сын
узла v (если такое существует), называется
правым поддеревом узла v. Все узлы в
расположены левее всех узлов в
.
Двоичное
дерево обычно представляют в виде двух
массивов ЛЕВЫЙСЫН и ПРАВЫЙСЫН. Пусть
узлы двоичного дерева занумерованы
целыми числами от 1 до
.
В этом случае ЛЕВЫЙСЫН[i]=j
тогда и только тогда, когда узел с номером
j
является левым сыном узла с номером i.
Если у узла i нет левого сына, то
ЛЕВЫЙСЫН[i]=0. ПРАВЫЙСЫН[i] определяется
аналогично.
Двоичное
дерево называется полным, если для
некоторого целого числа k
каждый узел глубины меньшей k
имеет как левого, так и правого сына и
каждый узел глубины k
является листом. Полное двоичное дерево
высоты k
имеет ровно
узлов.
Многие алгоритмы, использующие деревья, часто проходят дерево (посещают каждый его узел) в некотором порядке. Известно несколько систематических способов сделать это. Мы рассмотрим три широко распространенных способа: прохождение дерева в прямом порядке, обратном и внутреннем.
Определение.
Пусть Т — дерево о корнем
и сыновьями
,
.
Приk=0
это дерево состоит из единственного
узла
.
Прохождение дерева Т в прямом порядке определяется следующей рекурсией:
1)
посетить корень
,
2)
посетить в прямом порядке поддеревья
с корнями
в указанной последовательности.
Прохождение дерева Т в обратном порядке определяется следующей рекурсией:
1)
посетить в обратном порядке поддеревья
с корнями
в указанной последовательности,
2)
посетить корень
.
Прохождение двоичного дерева во внутреннем порядке определяется следующей рекурсией:
1) посетить во внутреннем порядке левое поддерево корня (если оно существует),
2) посетить корень,
3) посетить во внутреннем порядке правое поддерево корня (если оно существует)
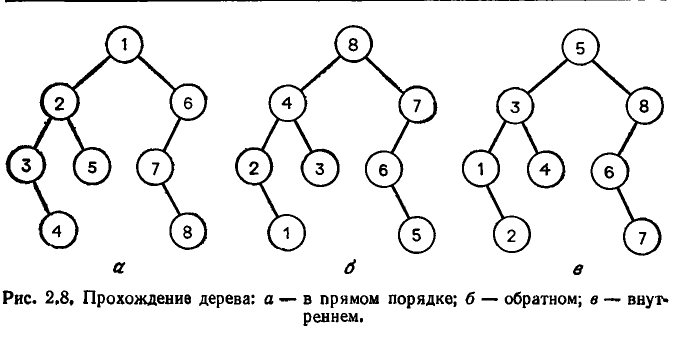
При
нумерации в прямом порядке все узлы
поддерева с корнем
имеют номера, не меньшие
.
Точнее, если
— множество потомков узла
,
то v будет номером некоторого узла из
тогда и только тогда, когда
.
Поставив в соответствие каждому узлу
v его номер в прямом порядке и количество
его потомков, легко определить, является
ли некоторый узел w потомком для v. После
того как номера присвоены (в соответствии
с прямым порядком) и вычислено количество
потомков каждого узла, на вопрос, является
ли w потомком для v, можно ответить за
фиксированное время, не зависящее от
размера дерева. Номера, соответствующие
обратному порядку, обладают аналогичным
свойством. Номера узлов двоичного
дерева, соответствующие внутреннему
порядку, обладают тем свойством, что
номера узлов в левом поддереве для v
меньше v, а в правом поддереве больше v.
Таким образом, чтобы найти узел с номером
w, надо сравнить w с корнем
.
Если
,
то искомый узел найден. Если
,
то надо повторить этот процесс для
левого поддерева; если
,
то повторить процесс для правого
поддерева. В конце концов узел с номером
w будет найден.
Список основных операций навигации по дереву (операций доступа к компонентам дерева) [7 п.3.2; 13 п.6.1.2]:
Root(): возвращает позицию корня дерева.
Parent(p): возвращает позицию «родителя» для вершины в позиции p.
LeftMostChild(p): возвращает позицию «самого левого сына» для вершины в позиции p.
RightSibling(p): возвращает позицию «правого брата» для вершины в позиции p.
Element(p): возвращает элемент дерева (хранимую информацию) для вершины в позиции p.
isInternal(p): проверяет, является ли p позицией внутренней вершины (не листа) .
isExternal(p): проверяет, является ли p позицией листа дерева.
isRoot(p): проверяет, является ли p позицией корня.
Для варианта с последовательным доступом к компонентам аргумент «позиция» (номер) становится не нужным, все операции привязаны к текущей позиции.
Для представления деревьев используются и массивы, и (нелинейные) связные списковые структуры данных (с указателями) и смешанные способы представления. В частности, представление структуры дерева может быть отделено от хранилища информации, привязанной к вершинам (и ребрам) дерева.
Видимо самый простой способ представления – основан на том, что для каждой вершины (не корня) однозначно определена родительская вершина. Дерево с (пронумерованными) вершинами 1..n представляется вектором v[1..n], где v[i] – номер родительской вершины для вершины i . Ясно, что для такого представления хорошо реализуется операция перехода к родителю, но неэффективно – операции перехода к сыновьям.
В основу представления бинарного дерева может быть положен принцип нумерации вершин. Каждая вершина дерева получает порядковый номер p(v):
• если v является корнем, то p(v) = 1;
• если v - левый сын вершины u, то p(v) = 2*p(u);
• если v - правый сын вершины u, то p(v) = 2*p(u)+ l.
Эта нумерационная функция известна как уровневая нумерация (level numbering) вершин бинарного дерева, поскольку нумерует вершины (начиная с корня) на каждом уровне (сверху вниз) в возрастающем порядке слева направо, но пропускает номера отсутствующих вершин, соответствующего полного бинарного дерева. Бинарное дерево представляется вектором, в котором вершине v соответствует элемент с индексом p(v). Аналогичную нумерационную функцию и представление можно предложить и для деревьев с не более чем m сыновьями (у каждой вершины).
Все вышеприведенные операции навигации реализуемы для такого представления с константным временем выполнения. Но по памяти такое представление неэкономично для существенно-неполных деревьев, оно потребует примерно 2k единиц памяти, где k – длина самой длинной ветви (даже если такая ветвь только одна, а все остальные существенно короче). Т.к. в таком векторе имеется позиция для каждой вершины полного дерева, а в нашем дереве большая часть вершин этого полного дерева может отсутствовать, то мы можем получить экспоненциальный перерасход памяти.
Связное представление (с указателями) позволяет получить реализацию с константным временем выполнения основных операций навигации, с памятью пропорциональной количеству вершин дерева и избежать специфических ограничений статических структур при реализации операций модификации структуры дерева.
Реализация операций модификации структуры дерева (удаления и добавления вершин) существенно зависит от их специфики и условий применения и соответствующего этой специфике способа представления дерева.
Отметим, что деревья общего вида (с переменным числом сыновей большим двух) можно представлять бинарными, подходящим способом различая в представляющем бинарном дереве ребра связи (исходного дерева) с родителем и ребра связи с братьями, как показано на рисунке (пунктиром соединены вершины представляющего дерева, ассоциируемые с вершинами-братьями исходного дерева):
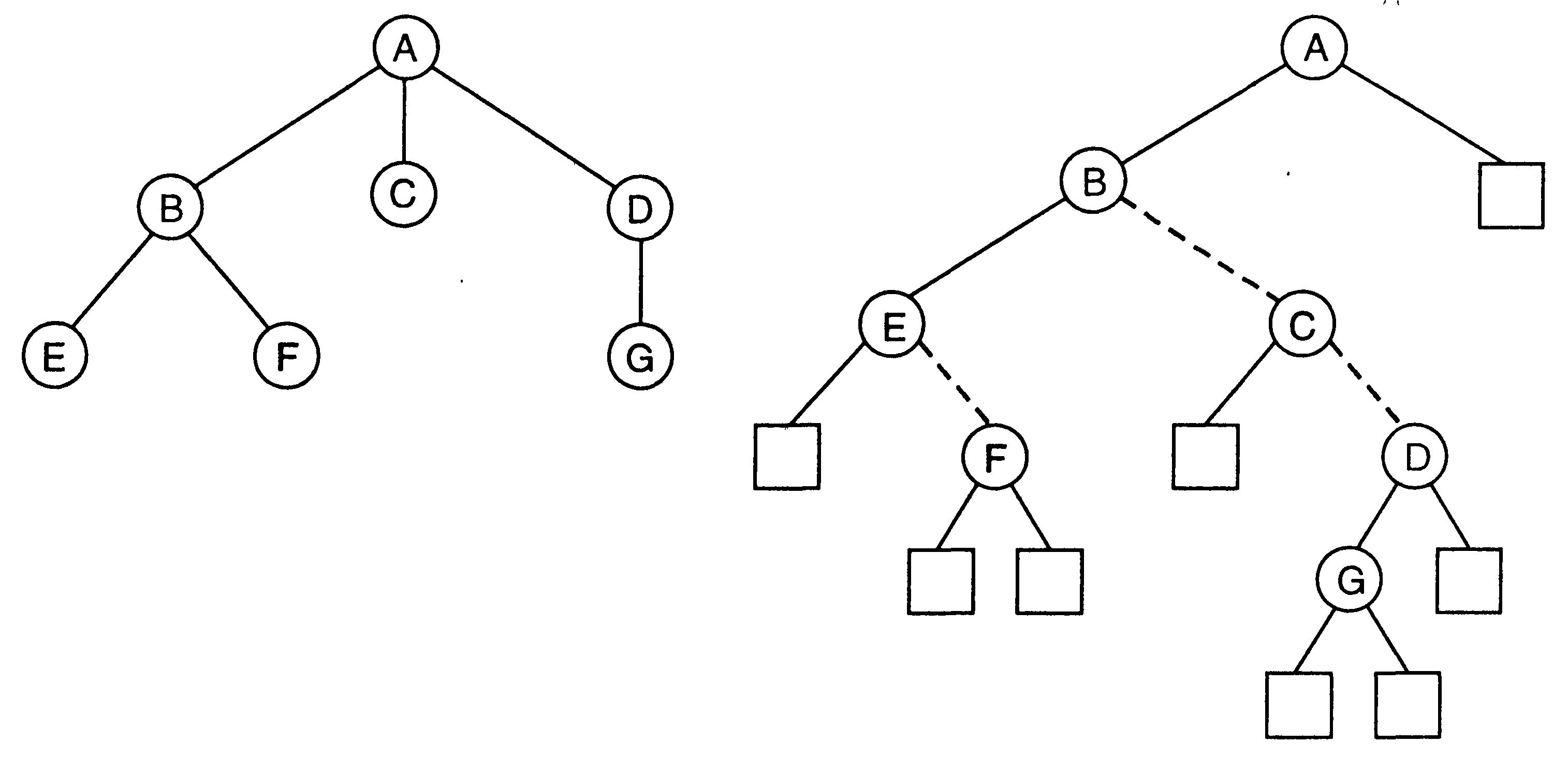
Дерево по определению обладает рекурсивной структурой. Это обстоятельство создает условия использования рекурсивных процедур. Процедуру, которая прямо или косвенно обращается к себе, называют рекурсивной. Применение рекурсии часто позволяет давать более прозрачные и сжатые описания алгоритмов, чем это было бы возможно без рекурсии.
Рассмотрим определение прохождения двоичного дерева во внутреннем порядке. При создании алгоритма, который присваивает узлам номера в соответствии с внутренним порядком, хорошо было бы отразить в нем определение прохождения во внутреннем порядке. Один из таких алгоритмов приведен ниже. Заметим, что он рекурсивно обращается к себе для нумерации поддерева.
Алгоритм 2.1. Нумерация узлов двоичного дерева в соответствии с внутренним порядком
Вход. Двоичное дерево, представленное массивами ЛЕВЫЙСЫН и ПРАВЫЙСЫН.
Выход. Массив, называемый НОМЕР, такой, что НОМЕР[i]— номер узла i во внутреннем порядке.
Метод. Кроме массивов ЛЕВЫЙСЫН, ПРАВЫЙСЫН и НОМЕР, алгоритм использует глобальную переменную СЧЕТ, значение которой — номер очередного узла в соответствии с внутренним порядком. Начальным значением переменной СЧЕТ является 1. Параметр УЗЕЛ вначале равен корню. Cам алгоритм таков:
begin
СЧЕТ
1;
ВНУТПОРЯДОК(КОРЕНЬ)
end ?
Рекурсия дает несколько преимуществ и прежде всего простоту программ. Если бы приведенный выше алгоритм не был записан рекурсивно, надо было бы строить явный механизм для прохождения дерева. Двигаться вниз по дереву нетрудно, но чтобы обеспечить возможность вернуться к предку, надо запомнить всех предков в стеке, а операторы работы со стеком усложнили бы алгоритм.
а операторы работы со стеком усложнили бы алгоритм.
procedure ВНУТПОРЯДОК(УЗЕЛ):
begin
1.
if
ЛЕВЫЙСЫН[УЗЕЛ]
0 then
ВНУТПОРЯДОК(ЛЕВЫЙСЫН[УЗЕЛ]);
2.
НОМЕР[УЗЕЛ]
СЧЕТ;
3.
СЧЕТ
СЧЕТ + 1;
4.
if
ПРАВЫЙСЫН[УЗЕЛ]
0
then
ВНУТПОРЯДОК(ПРАВЫЙСЫН[УЗЕЛ])
End
Вариант алгоритма во внутреннем порядке без рекурсии
Вход. Тот же, что у предыдущего алгоритма .
Выход. Тот же, что у предыдущего алгоритма .
Метод. При прохождении дерева в стеке запоминаются все узлы, которые еще не были занумерованы и которые лежат на пути из корня в узел, рассматриваемый в данный момент. При переходе из узла v к его левому сыну узел v запоминается в стеке. После
нахождения левого поддерева для v узел v нумеруется и выталкивается из стека. Затем нумеруется правое поддерево для v. При переходе из и к его правому сыну узел v не помещается в стек, поскольку после нумерации правого поддерева мы не хотим возвращаться в у; более того, мы хотим вернуться к тому предку
begin
СЧЕТ
1;
УЗЕЛ
КОРЕНЬ;
СТЕК
пустой;
левый:
while
ЛЕВЫЙСЫН[УЗЕЛ]
0
do
begin
затолкнуть УЗЕЛ в СТЕК;
УЗЕЛ
ЛЕВЫЙСЫН[УЗЕЛ]
end;
центр:
НОМЕР[УЗЕЛ1
СЧЕТ;
СЧЕТ — СЧЕТ+1;
if
ПРАВЫЙСЫН[УЗЕЛ[
0
then
begin
УЗЕЛ
ПРАВЫЙ СЫН[УЗЕЛ];
goto левый
end;
if СТЕК не пуст then
begin
УЗЕЛ
элемент в вершине СТЕКа;
вытолкнуть из СТЕКа;
goto центр
end
end