• Поисковые деревья (search tree). [13 гл.9]

Поисковое дерево – это упорядоченное дерево, имеющее следующие свойства:

• Каждая (нелистовая) вершина имеет по крайней мере две дочерние вершины;

• Каждая вершина с дочерними вершинами v₁, v₂, ..., v_d хранит d-1 ключей k₁  ...  k_d-1;

• Будем считать, что k₀= -, a k_d= +. Для каждого ключа k, хранящегося в поддереве вершины v_i (i=1..d), выполнено соотношение: k_i-1  k  k_i.

• Бинарное дерево поиска (с уникальными ключами¹⁹) [4 гл.12; 3 гл.12] – это бинарное упорядоченное дерево, у которого каждой вершине приписан уникальный ключ поиска, причем выполнено соотношение: ключи (всех) вершин левого поддерева < ключ родителя < ключи (всех) вершин правого поддерева. Отметим, что ключи в вершинах такого дерева расположены по возрастанию в соответствии с инфиксным (внутренним) обходом.

Отметим особенность (геометрического характера) таких деревьев – у вершин такого бинарного дерева допускается наличие правого сына при отсутствии левого, т.е. фиксируется не просто порядок на множестве дочерних вершин, но и их позиция (даже если позиция левого свободна). Хотя, с другой стороны, эту ситуацию можно трактовать как наличие двух детей, из которых левый – «пустой» (фиктивный)²⁰.

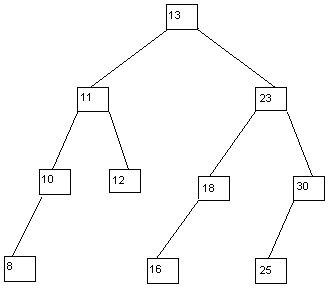
Для таких деревьев время поиска по ключу ≤ O(h), где h – высота дерева. Но при вставке новых вершин (с ключами) могут появляться длинные ветви, поэтому для времени поиска верхняя оценка в худшем O(n), где n – количество вершин в дереве. Статистический анализ показывает, что для бинарных поисковых деревьев с n вершинами оценка высоты в среднем O(log(n)) и она такая же для операций поиска, вставки, удаления и min с множествами мощности n. Поэтому бинарное дерево поиска хороший вариант для представления АТД «Множество», «Словарь»²¹ и «Очередь с приоритетом», но эффективна такая реализация только в среднем, т.е. только в среде, в которой случающиеся задержки выполнения операций некритичны, если общее время работы программы длительное и приемлемое для обрабатываемого объема входного потока.

• Сбалансированные деревья поиска (balanced search tree) [4 гл.13-14,18; 3 гл.13,16.3]. Верхнюю оценку в худшем для времени поиска получаем O(log(n)), если удается поддерживать сбалансированную структуру дерева поиска – не менее двух сыновей (почти) у каждой вершины и примерно одинаковая высота поддеревьев у каждого сына.

На сегодняшний день разработано несколько методов перестройки деревьев поиска, которые позволяют поддерживать сбалансированную структуру дерева поиска с приемлемыми расходами по времени, так чтобы общее время в худшем для операций поиска, вставки, удаления и min (АТД «Множество», «Словарь» и «Очередь с приоритетом») сохранялось O(log(n)). Балансировку структуры дерева можно проводить и по высоте, и по объему (весу) поддеревьев [18 п.6.4].

Для бинарных деревьев известны методы балансировки – АВЛ-деревья [13 п.9.2], красно-черные деревья (RB-tree) и их вариации.

• красно-черные деревья [4,]

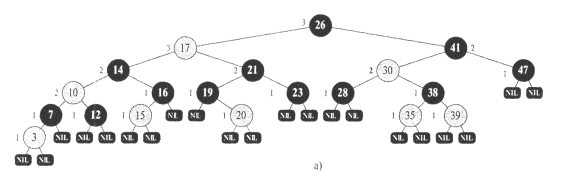
Красно-черное дерево - это двоичное дерево поиска, обладающее следующими свойствами(будем называть их RB свойствами):

• Каждый узел дерева покрашен либо в черный, либо в красный цвет.

• Листьями объявляются NIL-узлы ("виртуальные" узлы, являющиеся сыновьями узлов, которые в двоичном дереве поиска являлись листьями). Листья покрашены в черный цвет.

• Если узел красный, то оба его сына являются черными.

• На всех ветвях дерева, ведущих от его корня к листьям, число черных узлов одинаково.

Количество черных узлов на ветви от корня до листа называется черной высотой дерева. Перечисленные свойства гарантируют, что самая длинная ветвь, ведущая от корня к листу, не более чем в два раза длиннее любой другой ветви от корня к листу. Чтобы понять, почему это так, рассмотрим дерево с черной высотой . Кратчайшее возможное расстояние от корня до листа равно- когда все узлы черные. Длиннейшее расстояние от корня до листа равно, узлы при этом покрашены таким образом, что цвета чередуются (от корня к листу) так: красный, черный, красный, черный, …, красный, черный. Сюда нельзя добавить черные узлы, поскольку при этом нарушится свойство 4, из которого вытекает корректность понятия черной высоты. Поскольку согласно свойству 3 у красных узлов непременно черные наследники, в подобной последовательности недопустимы и два красных узла подряд. Таким образом, длиннейший путь, который мы можем сконструировать, состоит из чередования красных и черных узлов, что и приводит нас к удвоенной длине пути, проходящего только через черные узлы. Все операции над деревом должны уметь работать с перечисленными свойствами. В частности, при вставке и удалении эти свойства должны сохраниться. При соблюдении RB свойств, имеет место

Лемма[Кормен]. Красно-черное дерево с внутренними вершинами (не считая NIL листьев имеет высоту не более)

Из вышесказанного следует, что время выполнения операций поиска, нахождение минимального или максимального элементов с использованием красно-черных деревьев составляет . Отдельно необходимо рассмотреть операции вставки и удаления вершин дерева. Основная сложность анализа для этих операций заключается в том, что они могут испортить структуру красно-черного дерева, нарушив RB свойство.

Восстановление этих свойств требует перекраски некоторых вершин, а также выполнения операций вращения

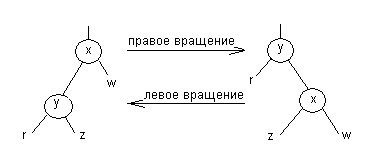
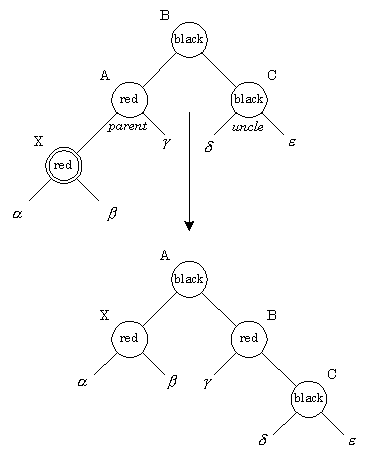
Операции левого и правого вращения являются обратными друг другу. При добавлении нового узла сначала ведется поиск места этого узла в дереве. Узел красится в красный цвет, его сыновья (NIL-узлы) окрашены в черные цвета. При вставке может быть нарушено RB-свойство 3, поскольку отец вставленной вершины также может быть окрашен в красный цвет. Если необходимо, мы перекрашиваем узел и производим поворот, чтобы сбалансировать дерево. Рассмотрим ситуацию, когда отец нового узла - красный: при этом будет нарушено свойство 3. Достаточно рассмотреть следующие два случая:

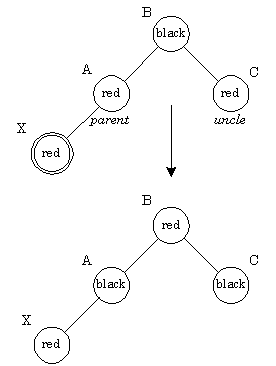
Красный отец, красный "дядя": Ситуацию красный-красный иллюстрирует рис. У нового узла X отец А и "дядя" С оказались красными. Простое перекрашивание избавляет нас от красно-красного нарушения. После перекраски нужно проверить "дедушку" нового узла (узел B), поскольку он может оказаться красным. Необходимо обратить внимание на распространение влияния красного узла на верхние узлы дерева. В самом конце корень красится в черный цвет. Если он был красным, то при этом увеличивается черная высота дерева

Красный отец, черный "дядя": На рис. представлен другой вариант красно-красного нарушения - "дядя" нового узла оказался черным. Здесь узлы может понадобиться вращать, чтобы скорректировать поддеревья. В этом месте алгоритм может остановиться из-за отсутствия красно-красных конфликтов и вершина дерева (узел A) окрашивается в черный цвет. Если узел X был в начале правым потомком, то первым применяется левое вращение, которое делает этот узел левым потомком. Каждая корректировка, производимая при вставке узла, заставляет нас подняться в дереве на один шаг. В этом случае до остановки алгоритма будет сделано 1 вращение (2, если узел был правым потомком). Метод удаления рассматривается аналогично.