
- •Оглавление
- •Структуры данных и эффективность алгоритмов.
- •Построение модели задачи. Процедурная абстракция и абстракция данных.
- •Основы анализа алгоритмов. [4 ч.1, гл.17, гл.34.]
- •Наихудшее и среднее время работы.
- •Пример 4. Рассмотрим вычисление полинома
- •Асимптотические обозначения.
- •Сложность задач и нижние оценки.
- •Труднорешаемые задачи и np-полнота. [8, 4 гл.34.]
- •Типы данных и структуры данных.
- •Абстрактные типы данных.
- •Последовательность (Sequence). [13 гл.4,5,11.1; 7 п.2.1-4; 3 гл.3-4; 4 п.10.1-3.]
- •Множество (Set). [7 гл.4.1-4; 13 п.10.2; 2 гл.4.]
- •Словарь (Dictionary, Map), другое название – ассоциативный массив [7 п.4.5-8; 3 гл.12; 2 п.4.10; 13 гл.8.].
- •Очередь с приоритетом (Priority queue). [7 п.4.10-11, п.5.6; 3 гл.9; 4 п.6.5; 2 п.4.10-13; 13 гл.7.]
- •Непересекающиеся множества (Disjoint Sets, Partitions, Разбиения) [7 п.5.5; 4 гл.21; 2 п.4.6-8.].
- •Деревья, графы и отношения общего вида. [13 гл.6,12; 7 гл.3, п.4.12, гл.6-7; 3 гл.17.]
- •Структуры данных как способы представления атд.
- •Линейные структуры данных.
- •Деревья.
- •Поисковые деревья (search tree). [13 гл.9]
- •Splay-дерево [19 п.4.3; 3 п.13.2]
- •Деревья цифрового (позиционного) поиска (DigitalSearchTrees,TrieTrees).[7 п.5.3; 3 гл.15.; 13 п.11.3]
- •Пирамиды (heap), другое название – сортирующее (или частично упорядоченное) дерево. [4 гл.6,19-20]
- •Структуры данных для непересекающихся множеств (отношения эквивалентности). [4 гл.21]
- •Рандомизированные структуры данных.
- •Случайная балансировка бинарных поисковых деревьев. [3 п.13.1]
- •Списки пропусков (Skip Lists). [13 п.8.6; 3 п.13.5]
- •Декартово дерево (Treap). [4 гл.13 Задачи 13-4; 20]
Сложность задач и нижние оценки.
Когда речь идет о конкретном алгоритме решения конкретной задачи, то целью анализа временной сложности этого алгоритма является получение оценки для времени в худшем или в среднем, обычно асимптотической оценки сверху O(g(n)), при возможности – и асимптотической оценки снизу (g(n)), а еще лучше - асимптотически точной оценки (g(n)).
Но при этом остается вопрос – а могут ли быть для этой задачи алгоритмы решения еще лучше. Этот вопрос ставит задачу о нахождении нижней оценки временной сложности для самой задачи (по всем возможным алгоритмам ее решения, а не для одного из известных алгоритмов ее решения). Вопрос получения нетривиальных нижних оценок очень сложный. На сегодняшний день имеется не так уж много таких результатов, но для некоторых ограниченных моделей вычислителей доказаны нетривиальные нижние оценки, и некоторые из них играют важную роль в практическом программировании.
Одной из задач, для которых известна нижняя оценка временной сложности, является задача сортировки:
Дана последовательность из n элементов a1,a2,... an, выбранных из множества, на котором задан линейный порядок.
Требуется найти перестановку этих n элементов, которая отобразит данную последовательность в неубывающую последовательность a(1),a(2),... a(n), т.е. a(i)≤a(i+1) при 1≤i<n.
При этом считается, что структура элементов последовательности неизвестна, но имеется возможность сравнивать эти элементы.
Для
этой задачи доказана нижняя оценка
временной сложности (nlog(n))
для
ограниченной модели вычислителя типа
«дерево решений» [4 п.8.1.], т.е. нет алгоритмов
(в определенном классе), решающих эту
задачу, лучше (по порядку). Пусть надо
упорядочить последовательность,
состоящую из
![]() различных элементов
различных элементов![]() .
Алгоритм, упорядочивающий с помощью
сравнений, можно представить в виде
дерева
.
Алгоритм, упорядочивающий с помощью
сравнений, можно представить в виде
дерева
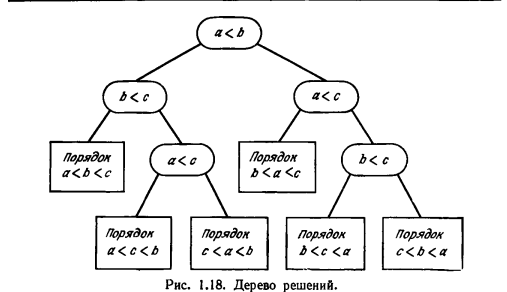
решений. Как правило, алгоритмы сортировки, в которых для разветвления используются сравнения, ограничиваются сравнением за один раз двух входных элементов. В противном случае, если за один шаг можно упорядочить некоторую подпоследовательность, то теряет смысл сама подобная постановка задачи.
Лемма
Двоичное дерево высоты h содержит не
более
![]() листьев. (индукция по
листьев. (индукция по![]() .)
.)
Теорема.
Высота любого дерева решений,
упорядочивающего последовательность
из
![]() различных элементов, не меньше
различных элементов, не меньше![]() (Любое дерево решений имеет
(Любое дерево решений имеет![]() листьев, Согласно лемме высота такого
дерева
листьев, Согласно лемме высота такого
дерева![]() ).
).
Следствие.
В любом алгоритме, упорядочивающем с
помощью сравнений, на упорядочение
последовательности из
![]() элементов
тратится не меньше
элементов
тратится не меньше
![]() сравнений при некотором с>0 и достаточно
большом
сравнений при некотором с>0 и достаточно
большом
![]() .
.
Доказательство.
Поскольку
![]() ,
то оценка снизу
,
то оценка снизу
![]()
Отметим, что алгоритмы, решающие эту задачу за такое время, известны, т.е. (nlog(n)) является асимптотически точной оценкой и для этой задачи и для этих алгоритмов ее решения.
В оценках временной сложности задач и алгоритмов их решения важное положение занимает метод сведения. Пусть у нас есть две задачи A и B, которые связаны так, что задачу A можно решить следующим образом:
Исходные данные к задаче A преобразуются в соответствующие исходные данные для задачи B.
Решается задача B.
Результат решения задачи B преобразуется в правильное решение задачи A .
В этом случае мы говорим, что задача A сводима к задаче B. Если шаги (1) и (3) вышеприведенного сведения можно выполнить за время O((n)), где, как обычно, n – «объем» задачи A , то скажем, что A (n)-сводима к B, и запишем это так: A (n) B. Вообще говоря, сводимость не симметричное отношение, в частном случае, когда A и B взаимно сводимы, мы назовем их эквивалентными. Следующие два самоочевидных утверждения характеризуют мощь метода сведения в предположении, что это сведение сохраняет порядок «объема» задачи.
Утверждение 1. (Нижние оценки методом сведения).
Если известно, что задача A требует не менее T(n) (нижняя оценка) времени и A (n)-сводима к B (A (n) B ), то задача B требует не менее T(n)-O((n)) времени.
Утверждение 2. (Верхние оценки методом сведения).
Если задачу B можно решить за время T(n) и задача A (n)-сводима к B (A (n) B), то A можно решить за время, не превышающее T(n)+O((n)).
Приведем нетривиальную нижнюю оценку для задачи построения выпуклой оболочки, полученной методом сведения
Пример 5. Задача о выпуклой оболочке – нижняя оценка [5 п.3.2.].
Выпуклой оболочкой множества точек Q (на плоскости) называется наименьший выпуклый многоугольник P такой, что каждая точка из Q находится либо на границе многоугольника P, либо в его внутренней области. Интуитивно можно представлять каждую точку множества Q в виде торчащего из доски гвоздя; тогда выпуклая оболочка имеет форму, полученную в результате наматывания на гвозди резиновой нити.
Дано множество Q, содержащее n точек на плоскости. Требуется построить их выпуклую оболочку, т.е. полное описание её границы.
Задача сортировки сводима за линейное время к задаче построения выпуклой оболочки, и, следовательно, для нахождения выпуклой оболочки n точек на плоскости требуется время (nlog(n)).
Продемонстрируем процедуру такого сведения:
Пусть заданы n положительных действительных чисел x1,x2,... xn.
Поставим в соответствие числу xi точку (xi, xi2). Все эти точки лежат на параболе y=x2.
Выпуклая оболочка этого множества точек, представленная в стандартном виде, будет состоять из списка точек множества, упорядоченного по значению абсциссы.
Один просмотр этого списка позволяет прочитать в нужном порядке значения xi.
Отметим, что алгоритмы, решающие задачу о выпуклой оболочке за такое время, известны, т.е. (nlog(n)) является асимптотически точной оценкой и для этой задачи и для этих алгоритмов ее решения.
Достаточно простой пример,
связанный с вычислением степенной
функции по модулю некоторого числа
![]() .
.
Пример
6. Даны
три натуральных числа
![]()
![]() и
и![]() .
Необходимо вычислить
.
Необходимо вычислить![]()
![]() .
Простой алгоритм основывается на
соотношении
.
Простой алгоритм основывается на
соотношении![]()
Программа 6.1.
y:= 1;
FOR i:=1 to n do y:= y * x (mod m)
и имеет
сложность O(n).
Однако можно существенно улучшить
алгоритм, используя двоичное разложение
показателя степени. Пусть
![]() ,
где
,
где![]() .
Тогда
.
Тогда
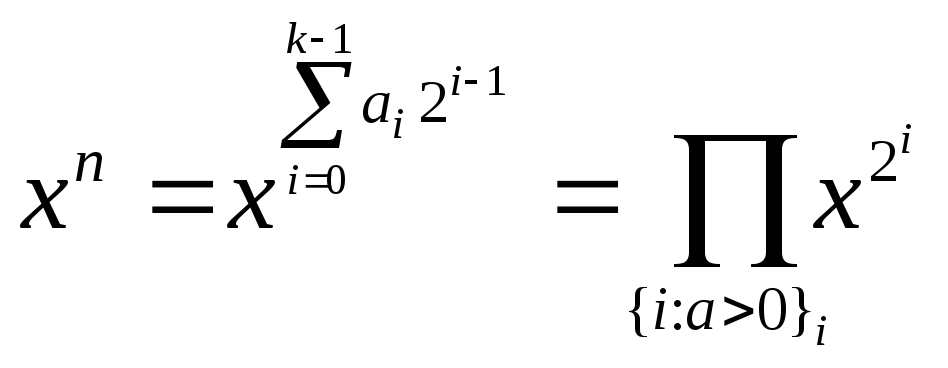
Это
соотношение показывает, что достаточно
провести
![]() итераций по двоичному разложению числа
итераций по двоичному разложению числа![]() ,
чтобы на каждой
,
чтобы на каждой![]() ой
итерации, в зависимости от значения
ой
итерации, в зависимости от значения![]() го
бита проводить домножение промежуточного
результата на
го
бита проводить домножение промежуточного
результата на![]() или на
или на![]() .
.
Программа 6.2.
y:= 1;
n1:=n;
x1:=x;
WHILE (n1>0) DO
IF n1 mod 2>=0
BEGIN
x1:=x1*x1 % mod m;
n1=n1 div 2
END
ELSE
BEGIN
y:=y*x mod m
n1:=n1-1
END
Временная сложность алгоритма равна O(log n). Величина выигрыша определяется по таблице при условии, что двоичное разложение n имеет k бит
|
k=56 |
|
|
|
k=128 |
|
|
Столь существенная разница связана с тем обстоятельством, что алгоритм 2 не делает повторные вычисления и существенным образом использует информацию, полученную на предыдущих шагах.
Большой интерес представляет связанная с предыдущей задача поиска дискретного логарифма:
Пусть
![]() нечетное простое число. Известны
натуральные
нечетное простое число. Известны
натуральные![]() и
и![]() и выполняется соотношение
и выполняется соотношение![]() .
Найти
.
Найти![]() .
.
Эта задача обратная по отношению к возведению в степень по модулю. Однако найти простого решения этой задачи не удается. Все известные алгоритмы требуют экспоненциального времени. На этом важном свойстве (свойстве односторонней вычислимости модульной экспоненты) основано множество алгоритмов современной криптографии.
Рассмотрим еще один пример [6 гл.8.], который иллюстрирует разные подходы к решению одной и той же задачи. Различные подходы дают различные временные оценки.
Пример 7. На
входе имеется вектор
![]() из n
вещественных чисел, на
выходе должна быть
получена
максимальная сумма любой непрерывной
последовательности элементов этого
вектора.
из n
вещественных чисел, на
выходе должна быть
получена
максимальная сумма любой непрерывной
последовательности элементов этого
вектора.
Например, если входной вектор есть x[0..9] = (31,-41,59,26, -53,58,97,-93,-23,84), то результатом решения задачи является сумма сегмента x[2..6], которая равна 187. Это максимальная сумма среди всех возможных сегментов массива x. Очевидным решением при всех положительных элементах вектора является сумма элементов всего входного вектора, а при всех отрицательных элементах - пустой сегмент с нулевой суммой.
Программа 7.1. Представляется естественной необходимость перебрать все сегменты входного вектора {[i..j]/0≤i≤j<n}. Вопрос о выборе порядка перебора пока отложим, и будем перебирать сегменты в соответствии с приведенным определением.
|
{1:} |
maxsofar:=0; |
1 |
|
{2:} |
FOR i:=0 TO n-1 DO |
n |
|
{3:} |
FOR j:=i TO n-1 DO BEGIN |
n+(n-1)+...1=n(n+1)/2 |
|
|
// Считаем сумму элементов сегмента x[i..j]: |
|
|
{4:} |
Sum:=0 |
n(n+1)/2 |
|
{5:} |
FOR k:=i TO j DO |
(1+...n)+(1+...(n-1))+...(1)
=
|
|
{6:} |
sum:=sum+x[k]; |
|
|
{7:} |
maxsofar:=max(maxsofar,sum) |
n(n+1)/2 |
|
|
END |
|
Оценим время работы этой программы:
Оператор в строке {1:} выполняется 1 раз.
Операторы заголовка цикла в строке {2:} выполняются n раз (и столько же раз выполняется оператор - тело этого цикла).
Операторы заголовка цикла в строке {3:} выполняются n-i раз для каждого i-го прохода внешнего цикла, получается n+ (n-1)+...1 раз.
Такое же количество раз выполняется оператор в строке {4:}.
Операторы заголовка цикла в строке {5:} выполняются j-i+1 раз для каждого i,j-го прохода пары (вложенных) внешних циклов, получается (1+...n)+(1+...(n-1))+...(1) раз.
Такое же количество раз выполняется оператор в строке {6:}.
Оператор в строке {7:} выполняется такое же количество раз как и операторы строки {3:}.
В целом время выполнения этой программы:
T(n)=1+n+3n(n-1)/2+2(n3/6+2n2+3n/4)=O(n3)
Фактически в данном конкретном случае (и как правило в большинстве других) нас мало интересует столь тщательный расчет этой функции T(n). Для упрощения расчета асимптотической оценки времени выполнения вполне достаточно использовать основные свойства О-символики [7 п.1.5.]:
Правило сумм. Если T1(n) и T2(n) имеют степени роста O(f(n)) и O(g(n)) соответственно, то T1(n)+T2(n) имеет степень роста O(max(f(n),g(n))). Из правила сумм в частности следует, что если f(n)≤g(n) для всех n, превышающих некоторое n0, то O(f(n)+g(n))= O(g(n)).
Если T1(n) и T2(n) – время выполнения программных фрагментов P1 и P2 соответственно, то T1(n)+T2(n) – время последовательного выполнения этих фрагментов. Если P1 и P2 связаны оператором if E then P1 else P2, то время выполнения такого оператора (сверху) оценивается как TE(n)+max(T1(n),T2(n)), где TE(n) – время выполнения сравнения E.
Правило произведений. Если T1(n) и T2(n) имеют степени роста O(f(n)) и O(g(n)) соответственно, то T1(n)*T2(n) имеет степень роста O(f(n)*g(n)). Из правила произведений следует, что O(c*f(n)) эквивалентно O(f(n)), если с – положительная константа.
Общее правило вычисления времени выполнения цикла заключается в суммировании времени выполнения каждой итерации цикла. Но в некоторых случаях достаточно точную оценку можно получить и более простым рассуждением: если T1(n) – длина цикла, а T2(n) – время выполнения тела цикла, то T1(n)*T2(n) – время выполнения цикла в целом.
Используя эти правила, время выполнения программы 5.1 можно оценить сверху O(n3) на том простом основании, что имеем трехкратный цикл, каждый из которых имеет длину не более n, а тело внутреннего цикла требует времени O(1).
Программа 7.2а. Повторные вычисления в предыдущей программе конечно хорошо видны, они происходят из того что просматриваемые сегменты вектора сильно перекрываются.
А повторность вычислений в строках (4-6) – явная небрежность (или неграмотность), при фиксированном i и возрастающем j сумму элементов сегментов x[i..j] так конечно не считают.
maxsofar:=0;
FOR i:=0 TO n-1 DO BEGIN Sum:=0;
FOR j:=i TO n-1 DO BEGIN
// Довычисляем сумму для сегмента x[i..j]:
sum:=sum+x[j];
maxsofar:=max(maxsofar,sum)
END
END
Время работы этой программы оценивается сверху O(n2), это гораздо лучше, чем в предыдущей программе, но повторные вычисления еще остались – при различных i многие просматриваемые сегменты тоже сильно перекрываются.
Программа 7.2b. В программе 7.2а мы воспользовались самым простым приемом оптимизации (и очевидным в данном случае) – сохранение результата предыдущего вычисления для его использования в последующем с целью устранения повторного вычисления. Отметим, что в более общем случае может возникать необходимость использования массива для массового сохранения результатов вычислений.
Для дальнейшей оптимизации воспользуемся еще одним приемом оптимизации – предварительная обработка информации с её сохранением для дальнейшего использования с целью устранения повторного вычисления.
Предварительно просчитаем суммы для всех сегментов x[0..j], тогда для сегментов x[i..j] суммы можно будет рассчитывать как разность сумм сегментов x[0..j] и x[0..(i-1)]. Для сохранения результатов предварительной обработки нам потребуется вектор:
cumarr: ARRAY[-1..(n-1)] OF REAL;
cumarr[-1]:=0;
FOR j:=0 TO n-1 DO cumarr[j]:= cumarr[j-1]+x[j];
maxsofar:=0;
FOR i:=0 TO n-1 DO BEGIN
FOR j:=i TO n-1 DO BEGIN
// Рассчитываем сумму для сегмента x[i..j]:
sum:= cumarr[j]- cumarr[i-1];
maxsofar:=max(maxsofar,sum)
END
END
Аккуратный анализ показывает, что время работы этой программы O(n2), т.е. не лучше чем у предыдущей программы, и явных повторных вычислений не видно.
Может быть, мы получили алгоритм с наилучшим (по порядку) временем? Рассмотрим вопрос о нижней оценке для этой задачи. Казалось бы, необходимость просмотра всех пар значений границ [i..j] дает квадратичную оценку. Но доказать эту необходимость неясно как... можно указать лишь тривиальную нижнюю оценку (n)=O(n). Она следует из того простого факта, что алгоритм должен обязательно просмотреть каждый элемент входного вектора, иначе именно он может оказаться основой для искомого максимума. Каких-либо вариантов повысить эту нижнюю оценку не видно...
Программа 5.3. Еще в рассуждении к самой первой программе мы отметили, что сегменты можно перебирать в различном порядке, но решили их перебирать в типовом порядке, отложив вопрос о других вариантах перебора. Обдумаем теперь именно этот вопрос, вполне возможно, что в случае каких-либо других вариантов перебора сегментов появятся более сильные возможности для устранения не только повторных вычислений, но и для исключения необходимости рассматривать некоторые (бесперспективные) сегменты.
Прежде всего, воспользуемся рассуждением известным как «разделяй и властвуй». Оно довольно часто дает хорошие алгоритмы, к тому же хорошо согласуется с нашими намерениями – при таком рассуждении сегменты будут перебираться в другом довольно изощренном специфическом порядке.
Рассмотрим следующее сведение исходной задачи к подзадачам - сегмент с максимальной суммой находится:
либо в левой половине исходного вектора,
либо в правой его половине,
либо левый его конец находится в левой половине, а правый его конец - в правой.
Осталось только выбрать максимальное из решений этих трех подзадач.
Рассмотрим параметризированный вариант исходной задачи – найти максимальную сумму по всем сегментам в сегменте x[i..j], и оформим в виде рекурсивной функции maxsofar решение этого варианта исходной задачи. Будем считать, что у нас имеется функция maxsofar3, которая решает третью подзадачу.
Будем считать n степенью двойки, это позволит устранить технические детали, которые отвлекают от основных рассуждений, но не вносят каких-либо важных изменений в наши рассуждения. Тогда решение исходной задачи получим вызовом maxsofar(0,n-1).
FUNCTION maxsofar(i,j:INTEGER):REAL; BEGIN
IF i>j THEN maxsofar:=0 //сегмент пустой
ELSE IF i=j THEN maxsofar:=max(0,x[i])//сегмент одноэлементный
ELSE BEGIN m:=(i+j+1) DIV 2; //находим середину
max1:=maxsofar(i,m-1); //решаем левую подзадачу
max2:=maxsofar(m,j); //решаем правую подзадачу
max3:=maxsofar3(i,j,m); //решаем третью подзадачу
maxsofar:=max(max1,max2,max3)
END END
Теперь рассмотрим третью подзадачу maxsofar3(i,j,m) – найти максимальную сумму по всем сегментам {[l..u]/i≤l<m≤u≤j}.
Эта максимальная сумма равна сумме двух максимальных сумм:
по всем сегментам с правым концом (m-1): {[l..(m-1)]/i≤l<m}
и по всем сегментам с левым концом m: {[m..u]/m≤u≤j}
FUNCTION maxsofar3(i,j,m:INTEGER):REAL; BEGIN
maxL:=0; sum:=0; FOR k:=m-1 DOWNTO i DO
BEGIN sum:=sum+x[k]; maxL:=max(maxL,sum) END;
maxU:=0; sum:=0; FOR k:=m TO j DO
BEGIN sum:=sum+x[k]; maxU:=max(maxU,sum) END;
maxsofar3:= maxL+maxU END
Время
работы этой программы T3(j-i+1)=![]() .
.
Теперь оценим время работы программы 7.3. Для алгоритмов, основанных на рассуждении сведением к подзадачам, оценка времени работы естественным образом описывается рекуррентными соотношениями. В частности в нашем случае:
T(n)= 2*T(n/2)+T3(n),
где T(n/2) – время решения для первых двух подзадач (левой и правой), а T3(n)=O(n) - время решения третьей подзадачи. Вообще-то надо еще добавить константу для вспомогательных действий и сборки общего решения, но можно считать, что это включено в T3(n). Теперь остается решить это рекуррентное соотношение.
Техника решения подобных рекуррентных соотношений достаточно хорошо разработана. Общую ситуацию (охватывающую наш случай) описывает теорема
Теорема
[4
п.4.3.].
Пусть
![]() и
и![]() - константы,
- константы,![]() - функция,
- функция,![]() определена при неотрицательных
определена при неотрицательных![]() формулой
формулой![]()
Где
под
![]() понимается или
понимается или![]() или
или![]() .
Положим
.
Положим![]() .
Тогда:
.
Тогда:
если
 для некоторого
для некоторого ,
то
,
то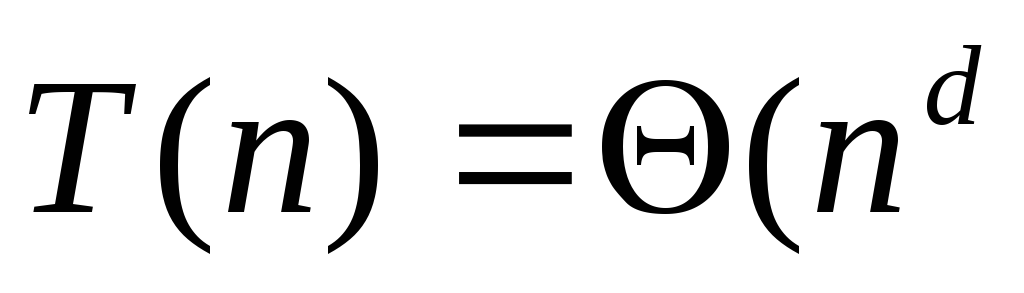 );
);если
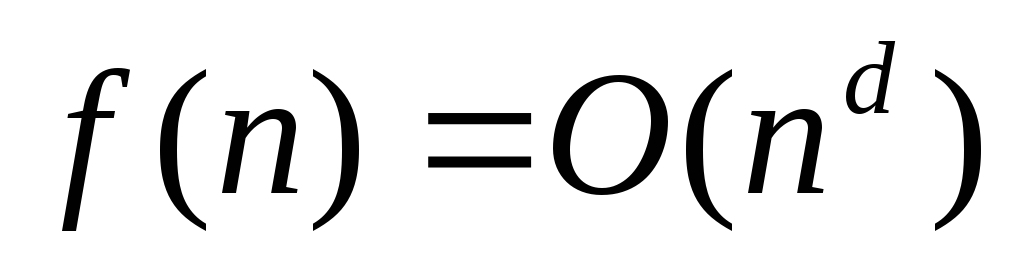 ,
то
,
то );
);если
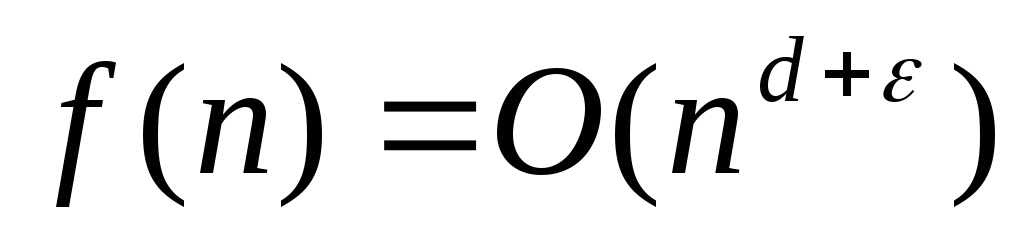 для некоторого
для некоторого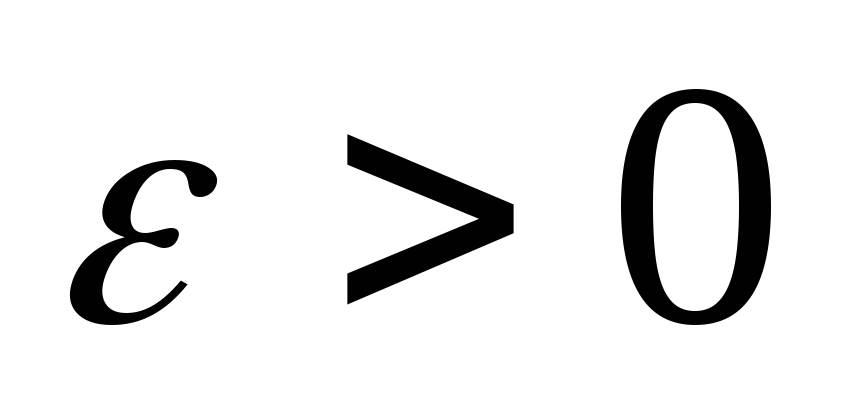 и если
и если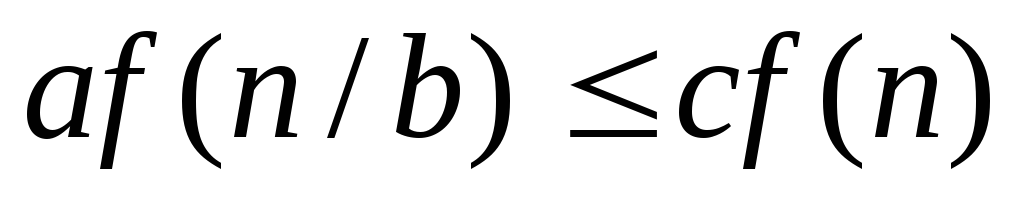 для некоторой константы
для некоторой константы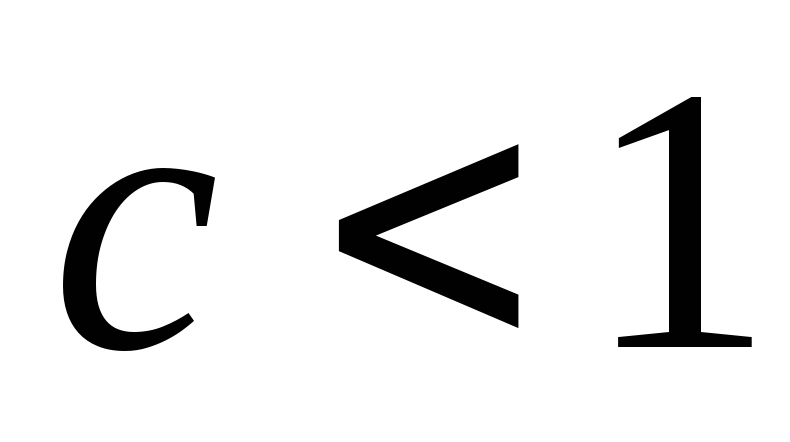 и достаточно больших
и достаточно больших ,
то
,
то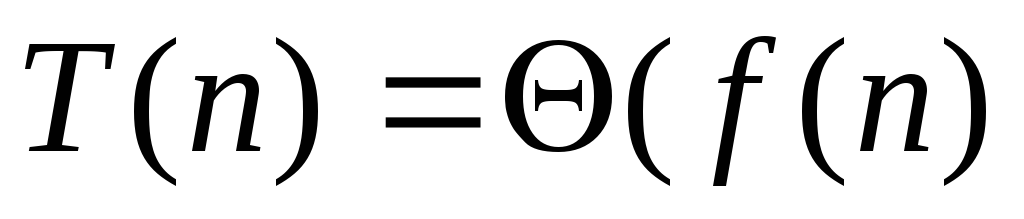 ).
).
Как
уже отмечалось разбиение задачи на
подзадачи с соответствующим решением
подзадач и последующей сборкой из
результатов их решения общего решения
исходной задачи довольно часто эффективно
используемая техника. При этом общее
время работы алгоритма обычно складывается
из суммы времен решения каждой из
подзадач T(з1) и T(з2) и времени на формирование
общего результата Т(з1![]() з2).
Как показывает эта теорема, выбором
подходящего разбиения на подзадачи с
соответствующими параметрами удается
минимизировать общее время решения
задачи.
з2).
Как показывает эта теорема, выбором
подходящего разбиения на подзадачи с
соответствующими параметрами удается
минимизировать общее время решения
задачи.
Для
случая нашей задачи имеем
![]() и
и![]() ,
согласно пункту 2 получаем
,
согласно пункту 2 получаем
![]() .
Итого, мы получили алгоритм существенно
лучше, чем предыдущие, причем из полученной
оценки времени следует очень важное
следствие - программа
5.3 решает исходную задачу, но просматривает
не все сегменты входного вектора,
поскольку общее количество этих сегментов
O(n2).
.
Итого, мы получили алгоритм существенно
лучше, чем предыдущие, причем из полученной
оценки времени следует очень важное
следствие - программа
5.3 решает исходную задачу, но просматривает
не все сегменты входного вектора,
поскольку общее количество этих сегментов
O(n2).
Сейчас видимо было бы полезно проанализировать какие сегменты эта программа не просматривает и на каком основании относит их к бесперспективным. Но мы попытаемся проанализировать возможности исключения сегментов из рассмотрения, опираясь на несколько иное рассуждение. Дело в том, что «разделяй и властвуй» - это один из вариантов рассуждения сведением к подзадачам, при котором исходная задача сводится к двум (или нескольким) подзадачам и сборке общего решения, при этом исходная задача разбивается на две такие же, но примерно половинного размера. Сбалансированное разбиение обычно и дает хороший эффект по времени.
С другой стороны, рассуждение методом последовательных уточнений тоже можно трактовать как рассуждение сведением к подзадачам, только разбиение осуществляется скорее наоборот – запредельно разбалансированное: на «почти всё» и «уточняющее дополнение». Представляется, что проанализировать возможности «отбраковки» бесперспективных сегментов на шаге «уточнения» будет легче.
Программа 5.4. Воспользуемся рассуждением методом последовательных уточнений:
Пусть (префиксная) часть вектора x[0..j] уже обработана, и мы имеем maxsofar - максимальную сумму по всем сегментам этой части вектора (т.е. пока мы видим только эту префиксную часть вектора до j-го его элемента).
Теперь нам надо уточнить имеющееся решение до решения нашей задачи для части вектора x[0..(j+1)](т.е. теперь видим на один элемент дальше).
Сегмент с максимальной суммой либо полностью лежит в x[0..j] и тогда maxsofar – решение и для расширенного префикса вектора, либо (j+1) – правый конец этого сегмента, а значит надо рассмотреть все сегменты {[z..(j+1)]/0≤z≤(j+1)}. Кстати, такую подзадачу «по всем сегментам с фиксированным правым концом» мы уже рассматривали в предыдущей программе, но время для неё O(j+2), а в целом для такого алгоритма тогда мы получим O(n2).
Но более важным для нас является следующее наблюдение:
Алгоритм, основанный на приведенном рассуждении методом последовательных уточнений, рассматривает сегменты в следующем порядке – все сегменты с правым концом j для каждого j в порядке возрастания.
Но если уже вычислена MaxEndingHere – максимальная сумма по всем сегментам с правым концом j, то не представляет труда уточнить значение этой переменной по всем сегментам с правым концом (j+1) – это просто max(MaxEndingHere+x[j+1],0).
Фактически для уточнения значения maxsofar на расширенный префикс x[0..(j+1)] нам нужна была именно MaxEndingHere, а значит необходимость просматривать сегменты с правым концом (j+1) просто совсем отпала...
maxsofar:=0; MaxEndingHere:=0;
FOR j:=0 TO n-1 DO BEGIN
// Пересчитаем максимальную сумму для сегментов с концом j:
MaxEndingHere:=max(MaxEndingHere+x[j],0);
// Пересчитаем максимальную сумму
// для всех сегментов в x[0..j]:
maxsofar:=max(maxsofar,MaxEndingHere)
END
Время работы этой программы (n).
Задача эта (в двумерном варианте) возникла в рамках работ по распознаванию образов, при этом сегмент с максимальной суммой элементов отражает наибольшее соответствие между двумя цифровыми изображениями. Первая программа требует ориентировочно 15 дней на решение задачи с характерным размером 100000 элементов, тогда как последний вариант программы решает ту же задачу за 5 миллисекунд. И увеличение скорости компьютера даже в 100 раз не вносит ничего существенного в эту ситуацию с учетом того, что такую задачу приходится решать многократно в рамках реальной задачи распознавания образов.
В заключение надо отметить, что асимптотические оценки конечно не охватывают всех важных аспектов вопроса о критериях оценки алгоритмов и программ. Приведем список соображений, позволяющих посмотреть на критерий времени выполнения с других точек зрения.
Если создаваемая программа будет использована только несколько раз, тогда стоимость написания и отладки программы будет доминировать в общей стоимости программы, т.е. фактическое время выполнения не окажет существенного влияния на общую стоимость. В этом случае следует предпочесть алгоритм, наиболее простой для реализации... хотя отсюда конечно не следует, что профессиональный программист в этом случае может позволить себе небрежность (граничащую с неграмотностью) в реализации алгоритма...
В определении асимптотической оценки фигурируют две константы (c>0 n0 ...). Если программа будет работать только с «малыми» входными данными, то степень роста времени выполнения (которая проявляется только для больших n>n0) может иметь меньшее значение, чем мультипликативная константа (c), присутствующая в формуле времени выполнения. Например, известен алгоритм целочисленного умножения, асимптотически самый эффективный, но он не используется на практике даже для больших задач, потому что его константа пропорциональности значительно превосходит подобные константы других, менее «эффективных» алгоритмов.
Известны примеры, когда эффективные алгоритмы требуют таких больших объемов памяти (и исключают возможность использования более медленных внешних средств хранения), что этот фактор сводит на нет преимущества эффективности алгоритма.
В численных алгоритмах точность и устойчивость не менее важны, чем их временная эффективность.
Широко распространенное на практике семейство задач – обработка входного потока в префиксном режиме: на вход поступает последовательность, а программа должна выдавать результат для каждого текущего элемента до начала поступления очередного. Если известны ограничения на скорость поступления элементов входного потока, то естественно нет достаточных оснований заниматься разработкой программы, позволяющей обрабатывать такой входной поток со скоростью, во много раз превосходящей скорость поступления элементов на входе.
