6.2. Взаимная перпендикулярность двух прямых общего положения в пространстве
Две прямые в пространстве будут взаимно перпендикулярными, если одна из них лежит в плоскости, перпендикулярной к другой прямой.
Пример (рис.6.6). Найти горизонтальную проекцию прямой а, проходящей через точку А и перпендикулярную к прямой b.
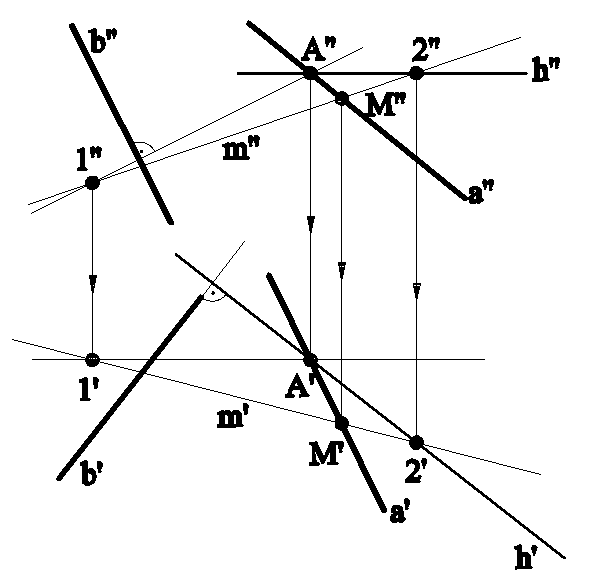
Рис.6.6
Решение: Проведем через точку А плоскость (h∩f), перпендикулярную заданной прямой b, так как любая прямая, лежащая в этой плоскости, будет перпендикулярна прямой b.
С помощью вспомогательной прямой m найдем точку M', принадлежащую искомой прямой а, и проведем проекцию а' этой прямой.
6.3. Взаимная перпендикулярность двух плоскостей общего положения в пространстве
Две плоскости в пространстве будут взаимно перпендикулярными, если одна из них содержит прямую, перпендикулярную к другой плоскости.
Пример (рис.6.7).
Через прямую l провести плоскость , перпендикулярную к заданной плоскости (h∩f).
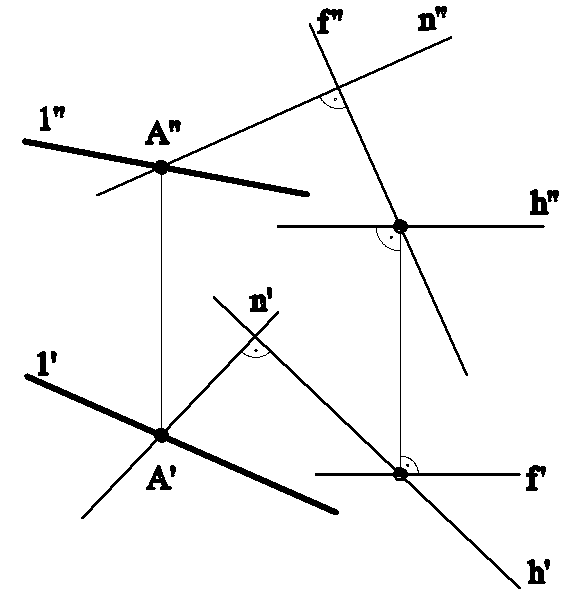
Рис.6.7
Решение: Через произвольную точку М на прямой l проведем прямую n, перпендикулярную к заданной плоскости (h∩f).
Условие перпендикулярности согласно п.6.1.
Пересекающиеся прямые l и n, определят искомую плоскость (n∩l).
7. Метрические задачи и способы их решения
Метрическими принято считать задачи, в условии или в решении которых присутствует численная характеристика.
К метрическим задачам относятся задачи на построение изображений фигур по их размерам или координатам из точек, измерение расстояний, углов, площадей и другие.
Метрические задачи бывают комплексными и включают в своем составе позиционные задачи.
Из всего многообразия метрических задач выделяют две задачи, которые называются основными метрическими задачами.
Первая задача - задача на перпендикулярность прямой линии и плоскости (п.6.1).
Вторая основная задача - задача на измерение расстояния между двумя точками способом прямоугольного треугольника.
Эти задачи называют основными потому, что на их основании можно решить любую другую метрическую задачу, то есть решение любой метрической задачи можно свести к решению основных метрических задач.
Кроме этого, метрические задачи можно решать и способами преобразования комплексного чертежа.
7.1. РЕШЕНИЕ МЕТРИЧЕСКИХ ЗАДАЧ В ОБЩЕМ ВИДЕ
Рассмотрим решение одной из метрических задач на примере, когда ее решение сводится к решению двух основных метрических задач.
Пример (рис.7.1).Измерить расстояние от точки А до плоскости (h∩f).
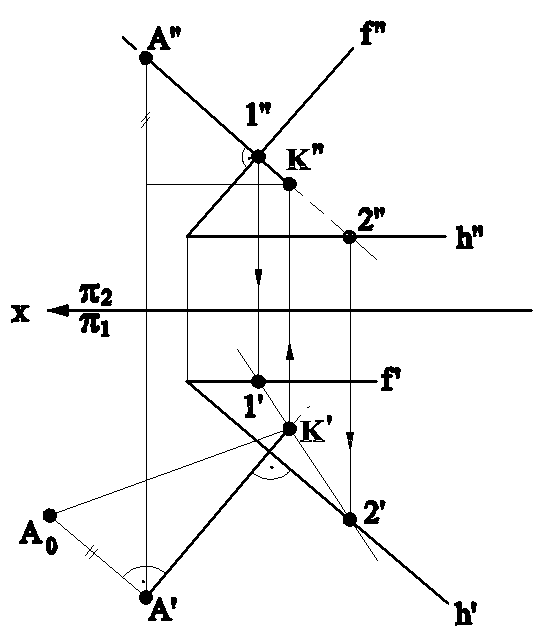
Рис.7.1
Решение:
1.Опустим из точки А перпендикуляр на плоскость (h∩f) и найдем его основание - точку К.
2.Способом прямоугольного треугольника измерим истинную величину отрезка АК.
Задача решена
АК=А0K'.
7.2. Решение метрических задач способами преобразования комплексного чертежа
Способами преобразования комплексного чертежа могут быть решены только те метрические задачи, которые имеют только один геометрический элемент, несущий на себе одну искомую численную характеристику.
Алгоритм решения метрической задачи с помощью преобразования комплексного чертежа сводится к следующему:
1) определяется геометрический элемент оригинала, несущий на себе искомую численную характеристику и,
2) определяется “решающее положение” оригинала по отношению к плоскости проекций. (Решающим положением оригинала называют такое положение, при котором геометрический элемент, несущий на себе искомую численную характеристику, может быть спроецирован на плоскость проекций без искажений).
Решающих положений может быть только четыре и им соответствуют и четыре известных задачи на преобразование комплексного чертежа.