3.2. Прямые и точки на плоскости. Главные линии на плоскости.

Если точка лежит на прямой, принадлежащей плоскости, то точка принадлежит этой плоскости: Аl  A.. Чтобы прямая линия принадлежала плоскости необходимо, чтобы две ее точки принадлежали этой плоскости.

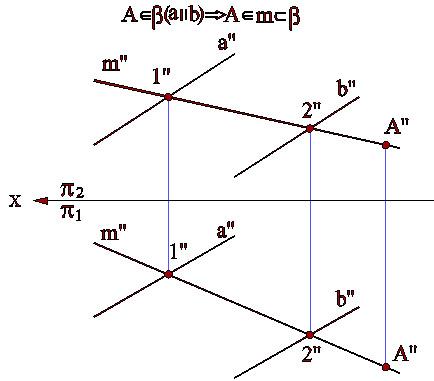
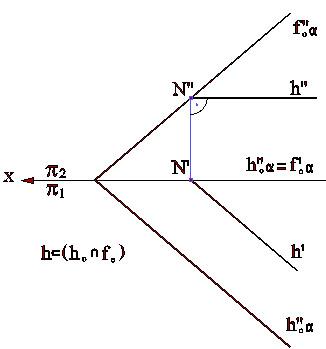
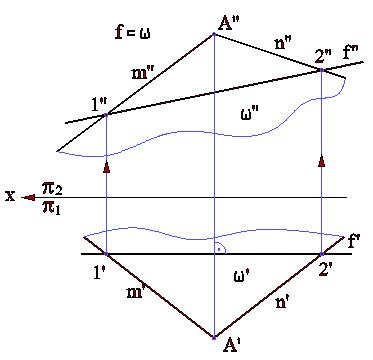
Рис.3.5 Рис.3.6 Рис.3.7

Линией уровня плоскости называют прямую линию, лежащую в плоскости и параллельную соответствующей плоскости проекций.

Соответственно различают: горизонталь плоскости - прямую h, параллельную горизонтальной плоскости проекций; прямую f, параллельную фронтальной плоскости проекций и профильную прямую р, параллельную профильной плоскости проекций (рис.3.6, 3.7, 3.8).

Горизонталей, фронталей и профильных прямых на чертеже может быть несколько. В этом случае их помечают индексами: 1, 2, 3 ... Например, h₁, h₂, h₃ ..., f₁, f₂, f₃ ...

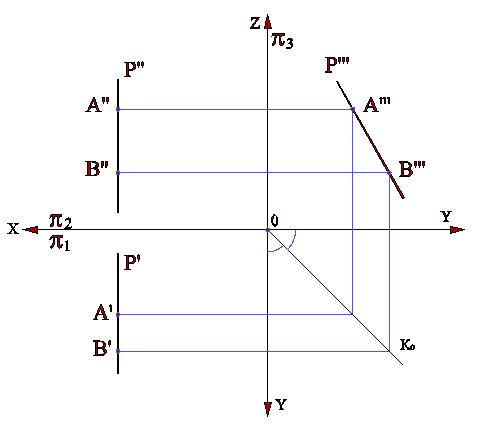
Рис.3.8

3.3. Линии наибольшего наклона плоскости к плоскостям проекций

Прямая, лежащая в плоскости общего положения и перпендикулярная к линии уровня или следу плоскости, называется линией наибольшего наклона плоскости к соответствующей плоскости проекций.

Линии наибольшего наклона плоскости  к горизонтальной и фронтальной плоскостям проекций показаны на рис.3.9а и 3.9б, 3.10а и 3.10б.

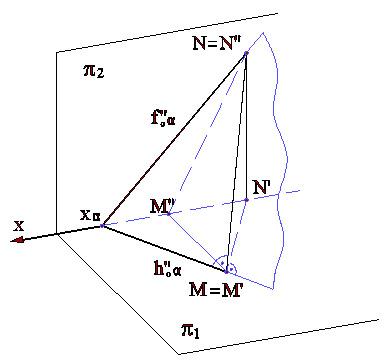
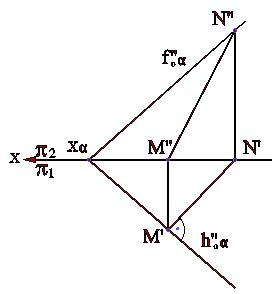
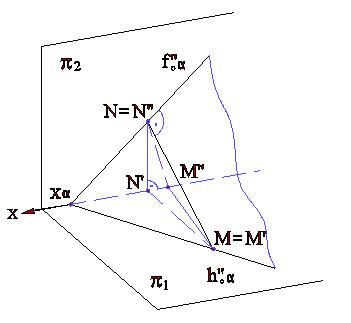
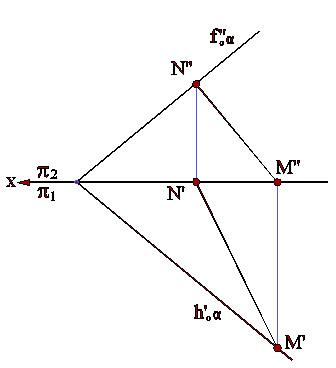
Рис.3.9а Рис.3.9б Рис.3.10а Рис.3.10б

На рис.3.11приведен пример линии наибольшего наклона плоскости, заданной плоской фигурой - параллелограммом АВСD (линия m) - по отношению к горизонтальной плоскости проекций ₁. Построение ясно из чертежа.

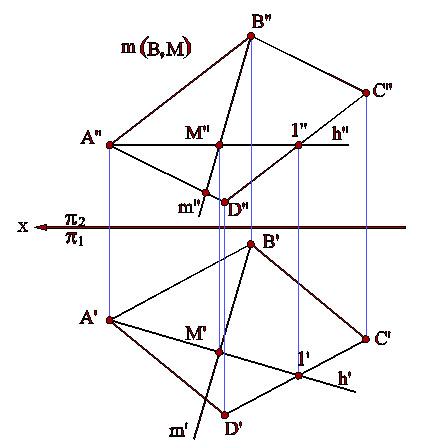
Рис.3.11

Поскольку линия наибольшего наклона перпендикулярна соответствующей линии уровня данной плоскости, то очевидно, что с помощью только одной линии - линии уровня плоскости по отношению к той или иной плоскости проекций, можно задать плоскость общего положения в пространстве. На рис.3.12 плоскость  задана линией наибольшего наклона к фронтальной плоскости проекций - линией n. Второй линией в этом случае является линия фронтали f, которую можно провести через любую точку линии n наибольшего наклона данной плоскости.

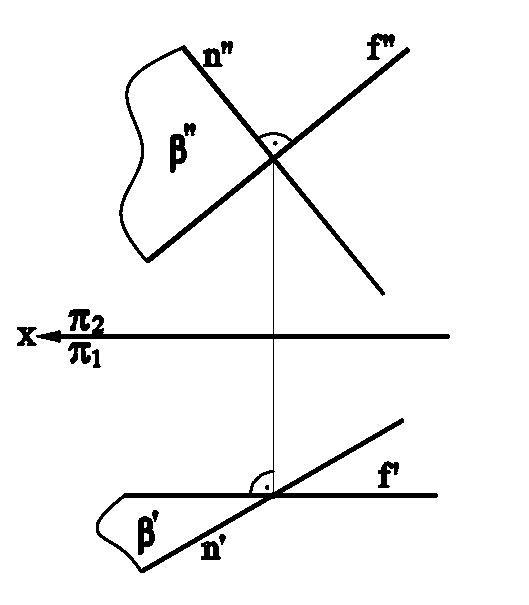
Рис. 3.12

Литература: Гордон В.О. и др. Курс н.г., 1988: с. 32-37; 42-49;62-64. Фролов С.А. Н.г., 1983.: с.34-42.

4. Взаимное положение прямых и плоскостей. Взаимная параллельность прямой и плоскости.

Из стереометрии известно: Если прямая параллельна какой-нибудь прямой, расположенной в плоскости, то она параллельна самой плоскости.

Пример 1 (рис.4.1). Найти горизонтальную проекцию прямой n, параллельной данной плоскости  (АВС).

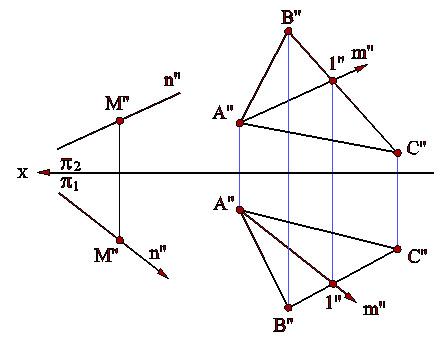
Рис.4.1

Решение:

Проведем в плоскости треугольника АВС прямую m”, параллельную n”, заданной прямой n.

Найдем ее горизонтальную проекцию m’ и параллельно ей через точку M’ проведем искомую прямую n’.

ВЗАИМНАЯ ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ

Из стереометрии известно: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Пример 2 (рис.4.2). Через точку А провести плоскость , параллельную плоскости (аb).

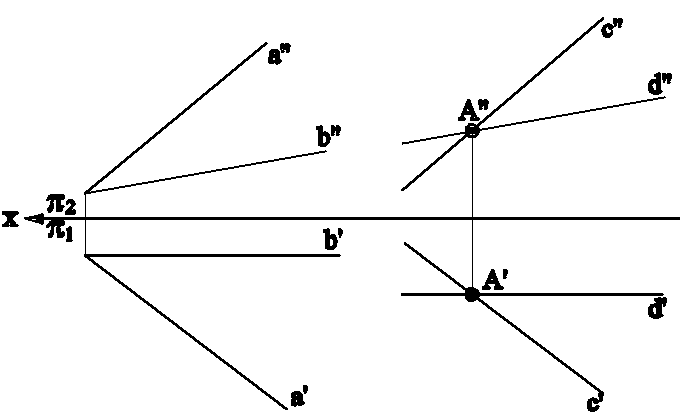
Рис.4.2

Решение:

Проведем через точку А прямые с и d, соответственно параллельные прямым а и b заданной плоскости , получим плоскость (сd), параллельную заданной плоскости.

Две плоскости (h₀f₀) и (h₀f₀) будут параллельны между собой, если одноименные следы этих плоскостей будут попарно параллельны (рис.4.3).

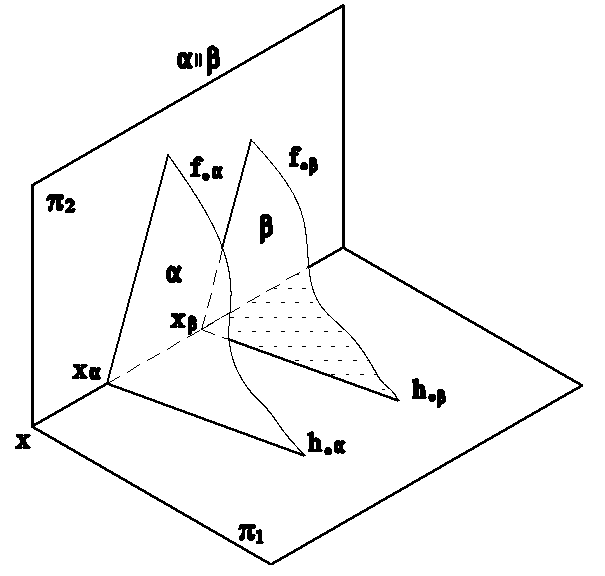
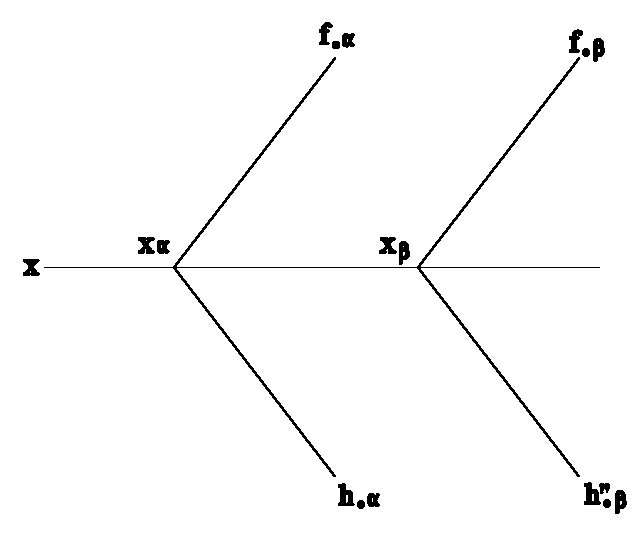
Рис.4.3а Рис.4.3б

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ.

Задача на взаимное пересечение прямой и плоскости может быть сведена к одному из трех типов задач:

1. Обе геометрические фигуры проецирующего положения по отношению к плоскостям проекций (рис.4.4а и 4.4б).

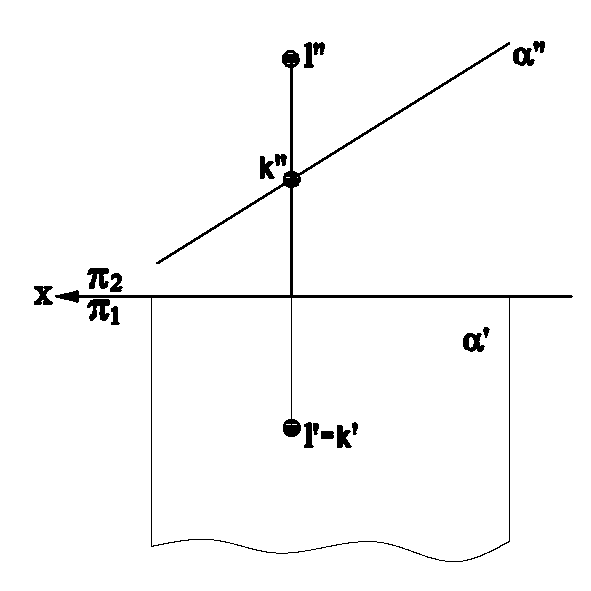
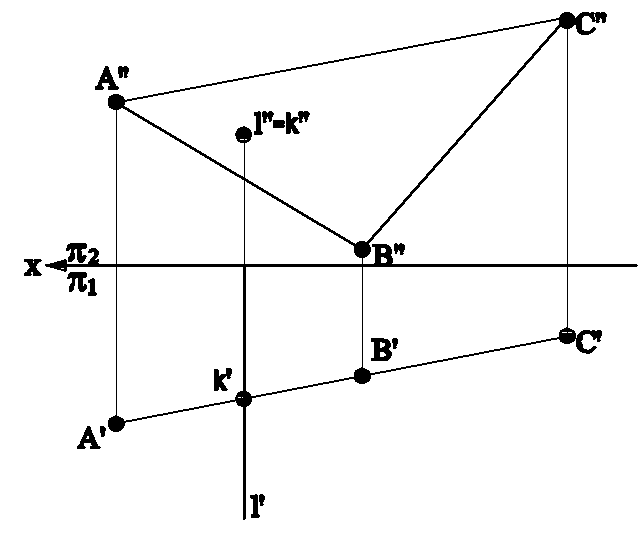
Рис.4.4а Рис.4.4б

В этом случае искомый элемент - точка пересечения на чертеже уже есть, ее надо только выделить и обозначить.

2. Одна из заданных фигур проецирующего положения в пространстве, а другая - общего (рис.4.5а и 4.5б).

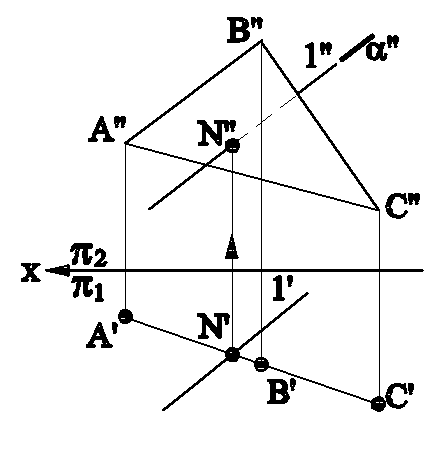
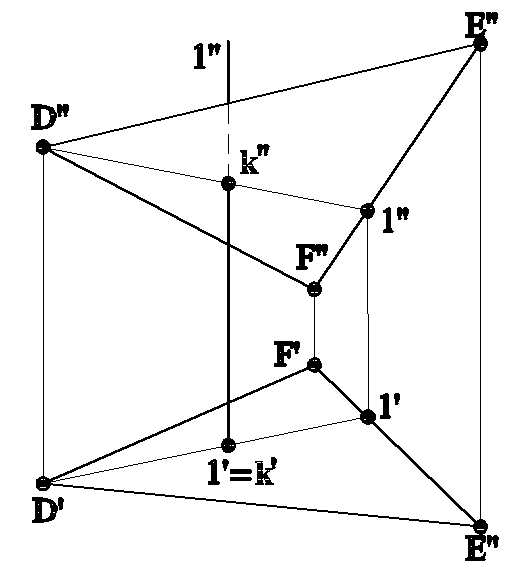
Рис.4.5а Рис.4.5б

В этом случае одна из проекций искомой точки пересечения на чертеже уже есть. Она принадлежит геометрической фигуре проецирующего положения, а другая ее проекция находится по принадлежности к фигуре непроецирующего положения.

3. Обе геометрические фигуры - линия и плоскость - общего положения в пространстве по отношению к плоскостям проекций.

В этом случае задача решается с помощью вспомогательной секущей плоскости в качестве “посредника”, которую проводят через заданную прямую.

На рис.4.6а и 4.6б приведены примеры пересечения прямой l с плоскостью треугольника АВС и прямой а с плоскостью , заданной следами.

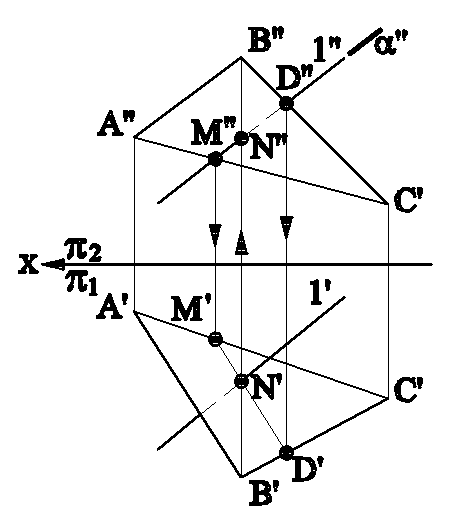
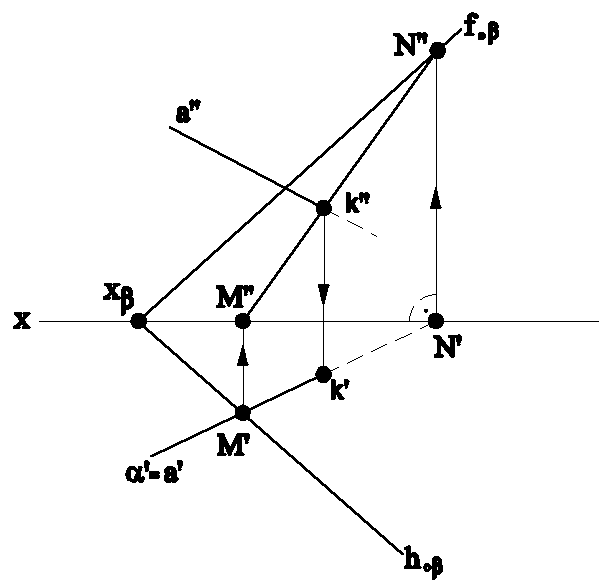
Рис.4.6а Рис.4.6б

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ

Эта задача может быть сведена к одному из трех типов задач, рассмотренных выше (случаи пересечения прямой с плоскостью).

1. Обе плоскости проецирующего положения по отношению одной или разным плоскостям проекций (рис.4.7).

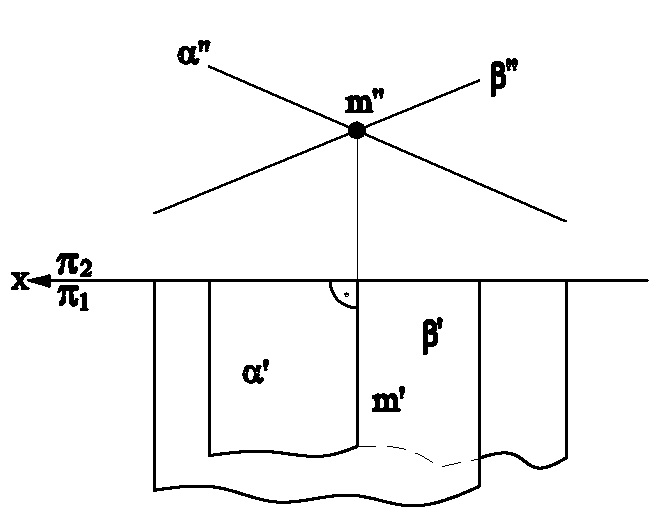
Рис.4.7

В этом случае искомая линия пересечения плоскостей на чертеже уже есть. Ее нужно только выделить и обозначить.

2. Одна из плоскостей проецирующего положения, а другая - общего положения (рис.4.8а и 4.8б).

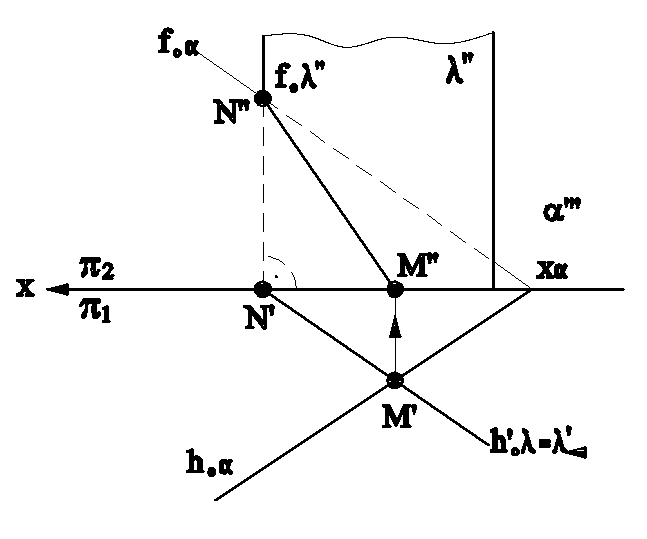
Рис.4.8а Рис.4.8б

3. Обе плоскости общего положения в пространстве.

В этом случае задача решается с помощью двух вспомогательных секущих плоскостей в качестве посредников. Такими посредниками будут проецирующие плоскости.

Пример 1 (рис.4.9). Найти линию пересечения двух плоскостей: (аb) и (c∩d).

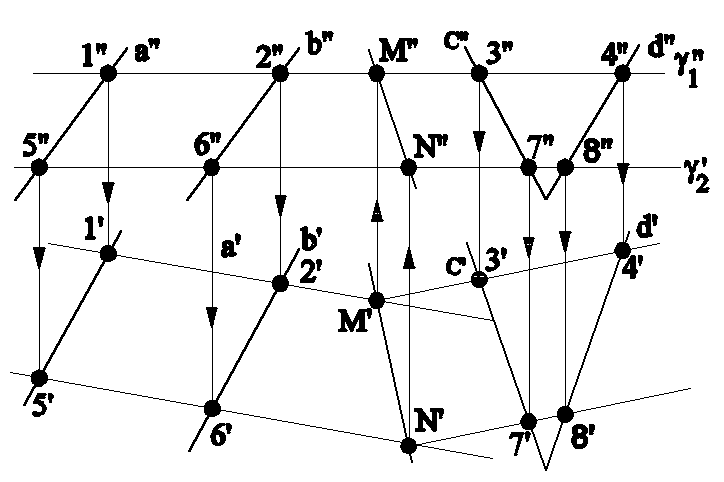
Рис.4.9

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ, ЗАДАННЫХ СЛЕДАМИ.

Линия взаимного пересечения плоскостей, заданных следами, проходит через точки пересечения их одноименных следов. Решение задачи показано на рис.4.10а и 4.10б.

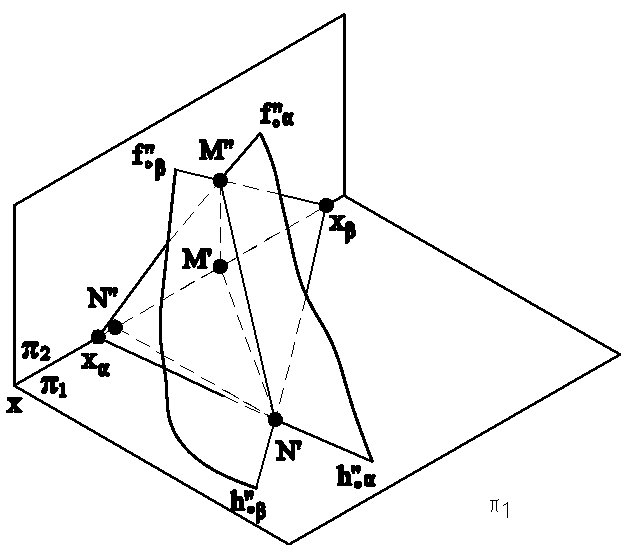
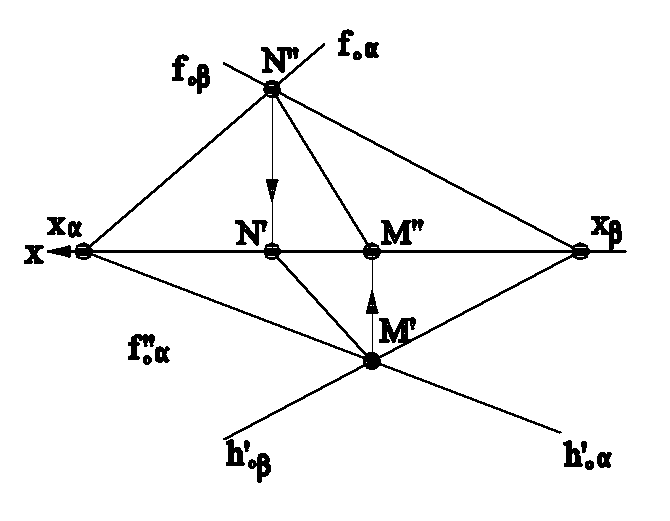
Рис.4.10а Рис.4.10б

Литература:

Фролов С.А. Начертательная геометрия. 2-е изд., изд.Машиностр. 1983., §§44;с.170.

Гордон В.О. и др. Курс начерт. геом., Глава IV до перпендикулярности.

Локтев В.О. Краткий курс начерт.геом. 1985. §§11, 12.

ИЗОБРАЖЕНИЕ МНОГОГРАННИКОВ

Многогранником называют тело, ограниченное плоскими многоугольниками. Многогранник, расположенный по одну сторону от плоскости его грани, называют выпуклым.

Грани, вершины и ребра многогранников связаны между собой соотношением, называемым теоремой Л.Эйлера: Г+В-Р=2, где: Г - число граней, В - число вершин и Р - число ребер.

Число граней многогранника не может быть меньше четырех, а сумма углов многоугольников, сходящихся в одной вершине, многогранных углов, не должно быть больше 2.

Основные виды многогранников: пирамида, призма, правильные многогранники и многогранники, имеющие соответствующие одинаковые двугранные углы.

Многогранник представляет собой частный случай замкнутой многогранной поверхности.

ВИДЫ МНОГОГРАННИКОВ

Призмой называют многогранник, у которого две одинаковые взаимно параллельные грани - основания, а остальные грани - параллелограммы.

Пирамида представляет собой многогранник, у которого одна грань (произвольный многоугольник) принимается за основание, а остальные (боковые) грани - треугольники с общей вершиной.

Правильными называются такие многогранники, у которых все грани - правильные равные многоугольники. Так как в каждой вершине многогранника должны сходиться не меньше трех многоугольников, а у правильного многоугольника все углы равны, то величина угла многоугольника (грани) должна быть меньше 2/3.

В правильном шестиугольнике углы равны 2/3, поэтому в правильном многограннике грань не может быть шестиугольником.

Из сказанного можно сделать вывод, что правильных многогранников может быт только пять. В качестве граней правильных многогранников могут быть только правильный треугольник, четырехугольник и пятиугольник.

Правильными многогранниками являются:

1. правильный четырехгранник или тетраэдр (грань - правильный треугольник),

2. правильный шестигранник (куб) или гексаэдр (грань квадрат),

3. правильный восьмигранник или октаэдр (грань правильный треугольник),

4. правильный двенадцатигранник или додекаэдр (грань - правильный пятиугольник),

5. правильный двенадцатигранник или икосаэдр (грань - правильный треугольник).

Правильные многогранники называют Платоновыми телами.

При изображении многогранника видимость его ребер и граней определяется с помощью конкурирующих точек.

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ МНОГОГРАННИКА

Задача на пересечение прямой с поверхностью многогранника решается с помощью вспомогательной секущей проецирующей плоскости, проводимой через заданную прямую (рис.4.12).

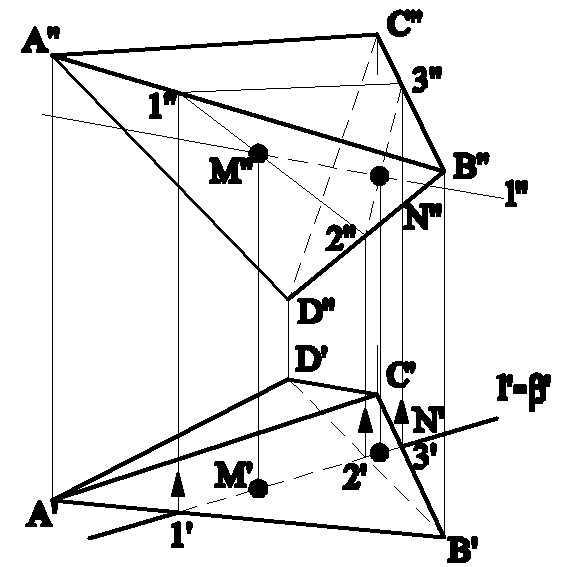
Рис.4.12

Вспомогательная горизонтально проецирующая плоскость (`) проведена через прямую l.

ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ ОБЩЕГО ПОЛОЖЕНИЯ

Задача на пересечение многогранника плоскостью общего положения решается с помощью вспомогательных секущих плоскостей в качестве “посредников”. На рис.4.12а приведен пример пересечения трехгранной призмы DEFD₁E₁F₁ плоскостью треугольника АВС.

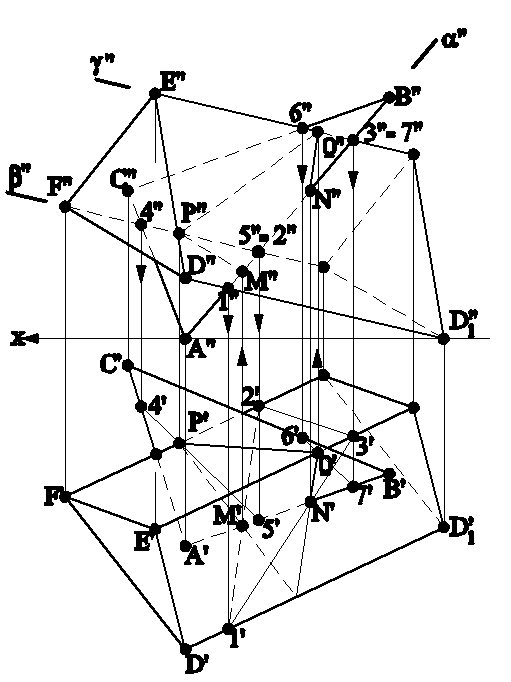
Рис.4.12а

Задача на рис.4.12а решена с помощью вспомогательных секущих плоскостей: (``), проведенной через сторону АВ треугольника АВС, которая пересекла призму по треугольнику 123, точки пересечения M и N c FD принадлежат искомой линии пересечения, и вспомогательных секущих плоскостей (`) и (``), с помощью которых найдены соответственно точки P и Q линии MPQN пересечения призмы DEFD₁E₁F₁ c треугольником АВС.

Определение видимости на чертеже не показано.