SBORNIK_PO_MATANU_ShKERINA_mIKhALKIN
.pdfБлок 32. Понятие предела функции.
Сформулируйте с помощью неравенств данное утверждение и его отрицание. Поясните их геометрический смысл.
1. |
lim |
f (x) = b. |
|
2. |
lim |
f (x) = +∞. |
|
||
|
x→∞ |
|
|
|
x |
→a+0 |
|
|
|
3. |
lim |
f (x) = b. |
|
4. |
lim f (x) = b. |
|
|
||
|
x→−∞ |
|
|
|
|
x→a |
|
|
|
5. |
lim |
f (x) = b. |
|
6. |
lim |
f (x) = b. |
|
||
|
x→+∞ |
f (x) = ∞. |
|
x |
→a−0 |
|
|
|
|
7. |
lim |
|
8. |
lim |
f (x) = b. |
|
|||
|
x→а |
f (x) = – ∞. |
|
x→a+0 |
f (x) = ∞. |
|
|||
9. |
lim |
|
10. |
lim |
|
||||
|
x→а |
f (x) = +∞. |
|
|
x→∞ |
f (x) = – ∞. |
|
||
11. |
lim |
|
12. |
lim |
|
||||
|
x→а |
f (x) = ∞. |
|
|
x→∞ |
f (x) = +∞. |
|
||
13. |
lim |
|
14. |
lim |
|
||||
|
x→а−0 |
f (x) = – ∞. |
|
|
x→∞ |
f (x) = ∞. |
|
||
15. |
lim |
|
16. |
lim |
|
||||
|
x→а−0 |
|
|
|
|
x→−∞ |
|
|
|
17. |
lim |
f (x) = +∞. |
|
18. |
lim |
f (x) = – ∞. |
|
||
|
x→а−0 |
|
|
|
|
x→−∞ |
|
|
|
19. |
lim |
f (x) = ∞. |
|
20. |
lim |
f (x) = +∞. |
|
||
|
x→а+0 |
|
|
|
|
x→−∞ |
|
|
|
21. |
lim |
f (x) = – ∞. |
|
22. |
lim f (x) = ∞. |
|
|||
|
x→а+0 |
|
|
|
|
x→+∞ |
|
|
|
23. |
lim |
f (x) = – ∞. |
|
24. |
lim |
f (x) = +∞. |
|
||
|
x→+∞ |
|
|
|
|
x→+∞ |
|
|
|
25. |
f(x)→b–0 |
при |
х→а–0. |
26. |
f(x)→b–0 |
при |
х→а+0. |
||
27. |
f(x)→b+0 |
при |
х→– ∞. |
28. |
f(x)→b+0 |
при |
х→+∞. |
||
29. |
f(x)→b+0 |
при |
х→а–0. |
30. |
f(x)→b–0 |
при |
х→+∞. |
||
41
Блок 33. Существенность условий в определении предела функции на бесконечности. Можно ли из
данного предложения сделать вывод, что lim f (x) = b? (Ответ обоснуйте и дайте геометрическую
x→+∞
интерпретацию.)
1.Найдется такое e>0, что для всех х выполняется неравенство |f(x)– b|<e.
2.Для любых e и с найдется такое x>c, что |f(x)– b|<e.
3.Для любого e найдется такое с, что из x>c следует |f(x)– b|<e.
4.Для любого e найдется такое с, что для всех x>c выполняется неравенство f(x)– b<e.
5. Для любого e>0 существует такое c>2, что для всех х>с выполняется неравенство |
|f(x)– b|<e. |
6.Для любого e>0 и всех х>0 справедливо неравенство |f(x)– b|<e.
7.Для любого e>1 найдется такое с, что для всех х>с выполняется неравенство |f(x)– b|<e.
8.Для некоторого 0<e<0,1 найдется такое с, что для всех х>с выполняется неравенство |f(x)– b|<e.
9.Для любого 0<e<0,01 найдется такое с, что для всех х>с выполняется неравенство |f(x)– b|<e.
10. |
Для любого |
0<e<2 |
и любого |
с существует такое х>с, |
что |
|f(x)– b|<e. |
Можно ли из данного |
|||
|
предложения |
сделать |
вывод, что |
lim f (x) = b? (Ответ |
обоснуйте и |
дайте |
геометрическую |
|||
|
|
|
|
x→−∞ |
|
|
|
|
||
|
интерпретацию.) |
|
|
|
|
|
|
|
|
|
11. |
Для любого e>0 существует такое c¹0, что для всех х< |
1 |
выполняется неравенство |
|f(x)– b|<e. |
||||||
|
||||||||||
|
|
|
|
|
с |
|
|
|
|
|
12. |
Существует такое e>0, что для всех х выполняется неравенство |
f(x)– b|<e. |
|
|
||||||
13. |
Для e=0,2 существует такое число c, что для всех х<с выполняется неравенство |f(x)– b|<e. |
|||||||||
14. |
Для любого e>0 и любого числа с |
существует х<с, для которого выполняется неравенство |f(x)– b|<e. |
||||||||
15.Для любого 0<e<1 существует такое с, что для всех х<с выполняется неравенство |f(x)– b|<e.
16.Для любого e>0 существует такое с<0, что для всех х<с выполняется неравенство |f(x)– b|<e.
17.Для любого e>0 существует такое с>1, что для всех х<с выполняется неравенство |f(x)– b|<e.
18. |
Существует такое e<0,03, что для любого х справедливо неравенство |f(x)– b|<e. |
19. |
Для любого 0<e<3 и всех x<3 справедливо неравенство |f(x)– b|<e. |
20. |
Для любого e>0 существует такое с, что для всех х<с выполняется неравенство |f(x)– b|<e. Можно ли из |
данного предложения сделать вывод, что lim xп = b? Ответ обоснуйте.
п→∞
21.Для e=0,1 существует такой номер по, что для всех п>по выполняется неравенство |xп – b|<e.
22.Для любого пÎN справедливо неравенство | xп – b|<0,001.
23.Для любого e>0 и любого пÎN существует такой номер по>п, что хпо - b <e.
24.Для любого e>0,1 существует такой номер по, что для всех п>по выполняется неравенство |xп – b|<e.
25.Для любого 0<e<1 существует такой номер по, что для всех п>по выполняется неравенство xп – b<e.
26.Существует такое e<0,001, что для всех пÎN справедливо неравенство |xп – b|<e.
27.Для любого e>0 и всех п>10 справедливо неравенство |xп – b|<e.
28.Для любого пÎN существует такой номер по, что для всех k>по, kÎN справедливо неравенство | xk –
b|< 1 .
п
29. Для любого пÎN существует такой номер kп, что |
|
x - b |
|
< |
1 |
. |
|
|
|||||
|
|
|
||||
|
|
kn |
|
|
п |
|
|
|
|
|
|
||
30. Для любого пÎN существует такой номер no, что для всех k>no выполняется неравенство
xk – b < 1 .
п
42
Блок 34. Существенность условий в определении предела функции в точке.
Можно ли из данного предложения сделать вывод о том, что lim f (x) = b? (Обоснуйте ответ и дайте
х→a
геометрическую интерпретацию.)
1.Для любого ε>0 существует 0<δ<1 такое, что для всех х, удовлетворяющих неравенству 0<|x– a|<δ, справедливо неравенство |f(x)– b|<ε.
2.Для любого ε> 1 существует δ>0 такое, что для всех х, удовлетворяющих неравенству
|
2 |
|
|
|
0<|x– a|<δ, справедливо неравенство |f(x)– b|<ε. |
|
|
||
3. |
Для любого 0<ε<1 существует δ>0 такое, что для всех х, удовлетворяющих неравенству 0<|x– a|<δ, |
|||
|
справедливо неравенство |f(x)– b|<ε. |
|
|
|
4. |
Для ε=0,001 существует |
δ=1 такое, что для всех х, удовлетворяющих неравенству |
|
|
|
|x– a|<δ, выполняется неравенство |f(x)– b|<ε. |
|
|
|
5. |
Для любого 0,1<ε<0,5 существует δ>0 такое, что для всех х, удовлетворяющих неравенству 0<|x– a|<δ, |
|||
|
выполняется неравенство |f(x)– b|<ε. |
|
|
|
6. |
Для любого ε>0 существует δ>0 такое, что для всех х, удовлетворяющих |
неравенству |
x– a<δ, |
|
|
справедливо неравенство |f(x)– b|<ε. |
|
|
|
7. |
Существует ε>0 такое, что для всех х, удовлетворяющих неравенству 0<|x– a|<ε, выполняется |
|||
|
неравенство |f(x)– b|<ε. |
|
|
|
8. |
Для любого ε>0 существует δ>0 такое, что для всех х, удовлетворяющих |
неравенству |
а– х<δ, |
|
|
справедливо неравенство |f(x)– b|<ε. |
|
|
|
9. |
Для любого ε>0 существует δ=2ε такое, что для всех х, удовлетворяющих неравенству 0<|x– a|<δ, |
|||
|
справедливо неравенство |f(x)– b|<3ε. |
|
|
|
10. |
Для любого ε>0 существует |
δ>0 такое, что для всех х, удовлетворяющих неравенству |
0<|x– a|<δ, справедливо |
|
|
неравенство f(x)– b<ε. |
|
|
|
11. |
Для любого ε>0 существует |
δ>0 такое, что для всех х, удовлетворяющих неравенству |
0<|x– xo|<δ, справедливо |
|
|
неравенство |f(x)– b|<ε. |
|
|
|
12. |
Для любого ε>0 существует |
δ>0 такое, что для всех х, удовлетворяющих неравенству |
0<|x– a|<δ, справедливо |
|
|
неравенство |f(x)– b|≤ε. |
|
|
|
13.Для любого 0<ε<1 существует δ>0 такое, что для всех х, удовлетворяющих неравенству 0<|x– а|<δ, справедливо неравенство |f(x)– b|≤ε.
14.Для любого ε>0 существует δ>0 такое, что для всех х, удовлетворяющих неравенству 0<|x– а|<δ, справедливо
неравенство |f(x)– b|<ε+0,1.
15. Для любого n N существует такое δ>0, что для всех х, удовлетворяющих неравенству |x– а|<δ, справедливо
1
неравенство |f(x)– b|< .
п
16. Для любого 0<ε<2 существует δ>0 такое, что для всех х, удовлетворяющих неравенству x– а<δ, справедливо неравенство |f(x)– b|<ε.
17.Для любого ε>0,01 и любого х, удовлетворяющих неравенству 0<|x– а|<0,01, справедливо |f(x)– b|<ε.
18.Для любого ε>0 существует δ>0 такое, что для всех х, удовлетворяющих неравенству |x– а|≤δ, справедливо |f(x)– b|<ε.
19.Для любого ε>0 существуют х, удовлетворяющие неравенству |x– а|≤δ, для которых |f(x)– b|<ε.
20. Для любого ε>0 существуют х, удовлетворяющие неравенству x– а>– δ, для которых |f(x)– b|<ε.
21.Для ε=0,02 и всех х, удовлетворяющих неравенству –0,01< x– а<0,01, справедливо |f(x)– b|<ε.
22.Для любого ε>0 существует δ>0, что для всех х, удовлетворяющих неравенству |x– а|<δ, справедливо |f(x)– b|<ε.
23. |
Для любого ε>0 и всех х, удовлетворяющих неравенству x<а+ε, справедливо |
|f(x)– b|<ε. |
|
24. |
Для любого ε>0,5 и всех х, удовлетворяющих неравенству а–0,1< x<а+0,1, справедливо |f(x)– b|<ε. |
||
25. |
Для любого 0<ε<4 и всех х, удовлетворяющих неравенству –4< x–a <4, справедливо |
|f(x)– b|<ε. |
|
26. |
Для ε=0,02 и всех х, удовлетворяющих неравенству 0<|x– a|<2, справедливо |
|f(x)– b|<ε. |
|
27. |
Для любого ε>0 и всех х, удовлетворяющих неравенству а–1< x<а+1, справедливо |
|
f(x)– b<ε. |
28.Существует 0<ε<1 такое, что для всех х, удовлетворяющих неравенству а– ε<x<а+ε, справедливо |f(x)– b|<ε.
29.Для любого ε>0 существуют х, удовлетворяющие неравенству 0<|x– а|<ε, для которых справедливо неравенство
|f(x)– b|<ε.
2 |
1 |
|
||
30. Для любого n N и всех х, удовлетворяющих неравенству 0<|x– а|< |
|
, выполняется неравенство |f(x)– b|< |
|
. |
|
|
|||
|
п |
|
п |
|
43
Блок 35. Определение предела числовой последовательности.
Докажите, используя определение предела числовой последовательности, что lim an = а.
n→∞
1. |
ап= |
3n − 2 |
; |
|
|
|
а= |
3 |
. |
|
|
|
|
|
|
|||||||||||||||
2n −1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||
3. |
ап= |
7n + 4 |
; |
|
а= |
7 |
|
. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2n + 1 |
|
2 |
||||||||||||||||||||||||||||
5. |
ап= |
7n −1 |
; |
|
|
|
а=7. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7. |
ап= |
9 − n3 |
|
; |
а= − |
|
1 |
. |
||||||||||||||||||||||
1 + 2n3 |
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
9. |
ап= |
1 − 2n2 |
|
|
; |
а= − |
|
1 |
. |
|||||||||||||||||||||
2 + 4n2 |
|
|
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
11. |
ап= |
n + 1 |
; |
|
|
|
а= − |
1 |
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 − 2n |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||
13. |
ап= |
1 − 2n2 |
|
|
; |
а= –2. |
||||||||||||||||||||||||
n2 + 3 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
15. |
ап= |
4 + 2n |
; |
|
а= − |
2 |
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
1 − 3n |
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||
17. |
|
3n −1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ап= |
|
; |
|
|
|
а= |
|
. |
|
|
|
|
|
|
||||||||||||||||
5n + 1 |
|
|
|
5 |
|
|
|
|
|
|
||||||||||||||||||||
19. |
ап= |
3 − 2n |
; |
|
|
|
а= − |
1 |
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
3 + 4n |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||
21. |
|
3n2 + 2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||
ап= |
|
|
|
|
|
; |
а= |
|
. |
|||||||||||||||||||||
4n2 − 1 |
|
|
4 |
|||||||||||||||||||||||||||
23. |
|
3n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ап= |
|
|
; |
|
а= –3. |
|||||||||||||||||||||||||
2 − n2 |
|
|||||||||||||||||||||||||||||
25. |
ап= |
5n + 15 |
; |
а= –5. |
||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
5 − n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
27. |
ап= |
4n − 3 |
; |
|
|
|
а=2. |
|
|
|
|
|
|
|||||||||||||||||
2n + 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
29. |
ап= |
23 − 4n |
; |
а=4. |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
|
2 − n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. ап= |
4n − 1 |
; |
|
|
|
|
|
|
|
а=2. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4. |
ап= |
|
2n − 5 |
; |
|
|
|
|
|
|
|
|
а= |
2 |
|
. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3n + 1 |
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||
6. |
|
|
4n2 + 1 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||||||||||||||||||
ап= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
а= |
|
|
|
. |
|
|
|
|
|
|||||||
|
3n2 + 2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||
8. |
|
|
|
4n − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ап= |
|
|
|
|
|
; |
|
|
|
а=2. |
|
|
|
|
||||||||||||||||||||||
2n + 1 |
|
|
|
|
||||||||||||||||||||||||||||||||
10. |
ап= − |
5n |
|
; |
|
|
а= –5. |
|
|
|
|
|||||||||||||||||||||||||
n + 1 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
12. |
ап= |
|
2n + 1 |
; |
|
|
а= |
2 |
. |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3n − 5 |
3 |
|
|
|
|
|||||||||||||||||||||||||||||||
14. |
ап= |
|
|
|
n |
|
|
; |
|
|
а= |
1 |
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
3n −1 |
3 |
|
|
|
|
|||||||||||||||||||||||||||||||
16. |
ап= |
|
|
3 − n2 |
; |
а= − |
1 |
. |
||||||||||||||||||||||||||||
|
1 + 2n2 |
2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
18. |
ап= |
|
1 − 2n2 |
|
; |
|
а= − |
|
1 |
. |
||||||||||||||||||||||||||
|
2 + 4n2 |
|
|
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
20. |
ап= |
1 + 3n |
; |
|
|
а= –3. |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
6 − n |
|
|
|
|
|
|
||||||||||||||||||||||||||||
22. |
ап= |
|
2n3 |
; |
|
|
а=2. |
|
|
|
|
|||||||||||||||||||||||||
n3 − 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
24. |
ап= |
3n3 |
; |
|
|
а=3. |
|
|
|
|
||||||||||||||||||||||||||
n3 −1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
26. |
ап= |
2n −1 |
; |
|
|
а= − |
2 |
. |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
2 − 3n |
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||||||||||
28. |
|
|
|
|
|
|
5n + 1 |
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
ап= |
|
|
|
|
; |
а= |
|
. |
||||||||||||||||||||||||||||
10n − 3 |
2 |
|||||||||||||||||||||||||||||||||||
30. |
ап= |
2n + 3 |
; |
|
а=2. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
44
Блок 36. Исследование вопроса о существовании предела функции в заданных точках.
Существует ли предел функции в указанных точках? Постройте эскиз графика этой функции.
|
|
|
если -1 < x < 1, |
|
|
х |
2 |
, |
если - 2 < x < -1, |
||||||
|
3х, |
|
|
|
|||||||||||
1. |
|
|
|
|
x = 1, |
2. |
|
|
|
|
|
|
x = -1, |
||
f(x)= 2, |
если |
|
f(x)= 0, |
|
если |
||||||||||
|
|
|
|
1 < x < 2. |
|
|
х, |
|
|
|
x > -1. |
||||
|
3х2 , |
если |
|
|
|
если |
|||||||||
|
х=0, х=1. |
|
|
|
х=0, |
|
х= –1. |
|
|
||||||
|
|
|
|
|
|
|
0, |
|
если x < 0, |
||||||
3. |
f(x)=sign x; |
|
|
|
4. |
|
|
|
|
если x = 0, |
|||||
|
|
|
f(x)= 1, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
если x > 0. |
||||
|
|
|
|
|
|
|
х3, |
||||||||
|
х=0, |
х=5. |
|
|
|
х= –4, |
|
|
х=0. |
|
|
||||
|
- х, |
если x < -2, |
|
- х3, |
если x < 1, |
||||||||||
5. |
|
|
если x = -2, |
6. |
|
|
|
|
|
если x = 1, |
|||||
f(x)= 5, |
f(x)= 0, |
|
|
||||||||||||
|
|
|
если x > -2. |
|
|
|
|
|
|
если x > 1. |
|||||
|
|
х, |
|
2х, |
|
||||||||||
|
х= –2, |
х=0. |
|
|
|
|
х=1, |
|
х=2. |
|
|
|
|||
|
х, |
если x < 2, |
|
|
х2 +1, если |
x < -1, |
|||||||||
7. |
|
|
если x = 2, |
8. |
|
|
|
|
|
если – 1 £ x < 0, |
|||||
f(x)= 1, |
f(x)= 2, |
|
|
||||||||||||
|
|
х +1, |
если x > 2. |
|
|
х, |
|
|
|
|
x ³ 0. |
||||
|
|
|
|
|
|
если |
|||||||||
|
х=0, х=2. |
|
|
|
х= –1, |
|
|
х=0. |
|
|
|||||
|
-1, |
если |
x < -2, |
|
2х, |
|
если |
x < 0, |
|||||||
9. |
|
|
если – 2 £ x < 0, |
10. |
|
|
|
|
|
0 £ x < 3, |
|||||
f(x)= x, |
f(x)= 3, |
|
если |
||||||||||||
|
|
|
|
|
x ³ 0. |
|
|
|
|
|
если |
x ³ 3. |
|||
|
1 + x2 , если |
|
х, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х= –2, |
х=0. |
|
|
|
|
х=0, х=3. |
|
|
|
|
||||
|
- 5х, если |
x < 1, |
|
- 2, |
|
если |
x £ 0, |
||||||||
11. |
|
|
|
1 £ x < 2, |
12. |
|
|
- 2, если 0 < x < 1, |
|||||||
f(x)= - 5, |
если |
f(x)= х |
|||||||||||||
|
|
|
|
x ³ 2. |
|
|
|
|
|
|
|
x ³ 1. |
|||
|
0, |
если |
|
х2 , |
|
если |
|
||||||||
|
х=1, х=2. |
|
|
|
|
х=0, х=1. |
|
|
|
|
|||||
|
х3, |
если |
|
x £ -1, |
|
-1, |
|
если |
– |
2 < x £ -1, |
|||||
13. |
|
|
|
– 1 < x £ 2, |
14. |
|
|
|
|
|
– 1 < x < 1, |
||||
f(x)= x - 2, если |
f(x)= х3, |
|
если |
||||||||||||
|
0, |
если |
|
x > 2. |
|
-1, |
|
если |
|
x ³ 1. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
х= –1, |
х=2. |
|
|
|
х= –1, |
|
х=1. |
|
|
|||||
|
2 - х, если |
x £ 0, |
|
|
2x, |
|
если |
x < 0, |
|||||||
15. |
|
|
|
0 < x £ 2, |
16. |
|
|
|
|
|
0 £ x £ 2, |
||||
f(x)= 2, |
если |
f(x)= 1, |
|
если |
|||||||||||
|
|
если |
x > 2. |
|
|
|
|
|
если |
x > 2. |
|||||
|
4x, |
|
|
x, |
|
||||||||||
|
х=0, х=2. |
|
|
|
|
х=0, х=2. |
|
|
|
||||||
|
- х2 |
, если |
x £ -1, |
|
|
|
2x -1, если |
x £ 0, |
|||||||
17. |
|
|
|
– 1 < x < 1, |
18. |
|
|
|
|
|
|
|
0 < x < 1, |
||
f(x)= -1, |
если |
f(x)= x2, |
если |
||||||||||||
|
x, |
если |
x ³ 1. |
|
|
|
1, |
|
если |
x ³ 1. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
х= –1, х=1. |
|
|
|
х=0, х=1. |
|
|
|
|||||||
|
- х, |
если |
|
x £ 1, |
|
|
|
x3 |
, |
если |
x £ 0, |
||||
19. |
|
|
1 < x < 4, |
|
|
|
|
|
|
|
0 < x < 1, |
||||
f(x)= -1, |
если |
20. f(x)= 1, |
|
если |
|||||||||||
|
|
|
|
x ³ 4. |
|
|
|
|
х2, если |
x ³ 1. |
|||||
|
x, |
если |
|
|
|
|
|
||||||||
|
х=1, х=4. |
|
|
|
|
х=0, х=1. |
|
|
|
||||||
45
|
- 2х, если |
x £ -2, |
|
|
||||
21. |
|
|
– 2 < x < 2, |
|||||
f(x)= 4, |
если |
|||||||
|
|
если |
x ³ 2. |
|
|
|||
|
x, |
|
|
|||||
|
х= –2, х=2. |
|
|
|
|
|
||
|
|
|
x £ -1, |
|
|
|||
|
- 5, |
если |
|
|
||||
|
|
|
|
|
|
1 |
|
|
23. |
|
|
– 1 < x < |
|
||||
f(x)= 5х, |
если |
|
, |
|||||
5 |
||||||||
|
|
|
|
|
|
|
||
|
|
|
x ³ |
1 |
|
|
|
|
|
10x, |
если |
|
. |
|
|
||
|
5 |
|
|
|||||
|
|
|
|
|
|
|
||
|
х= –1, |
х= |
1 |
. |
|
|
||||||
|
|
|
|
|||||||||
|
|
5 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х -1, |
если |
|||||||||
|
|
|||||||||||
25. |
|
|
|
|
|
|
|
|
|
|
|
|
f(x)= - х -1, если |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
||
|
0, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х= –1, |
х= |
1 |
. |
|
|
||||||
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
||||||
|
|
1 |
х, |
|
|
|
||||||
|
|
|
если |
|||||||||
|
2 |
|||||||||||
27. |
|
|
|
|
|
|
|
|
|
|
|
|
f(x)= 0, |
если |
|||||||||||
|
3 - x, если |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
||
|
1, |
|||||||||||
|
х=2, х=3. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2х +1, |
если |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29. |
2, |
eсли |
||||||||||
f(x)= |
|
|
1 |
|
|
|
|
|
|
|||
|
x + |
, если |
||||||||||
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1, |
если |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х=– |
1 |
, х= |
1 |
|
||||||
|
|
|
|
|||||||||
|
|
2 |
2 |
|
||||||||
x£ -1,
–1 < x < 1 ,
2
x³ 1 .
2
x < 2,
x = 2,
2 < x < 3,
х³ 3.
x< - 1 , 2
x= - 1 , 2
–1 < x < 1 ,
2 2
х³ 1 . 2
.
|
x2 -1, если |
x £ 0, |
|
|
|
||||||||||
22. |
|
|
0 < x < 3, |
||||||||||||
f(x)= x -1, |
если |
||||||||||||||
|
3, |
если |
x ³ 3. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
х=0, х=3. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x £ 0, |
|
|
|
|||||||||
|
- x -1, если |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
||||||
24. |
f(x)= x -1, |
если |
0 < x < |
|
|
, |
|||||||||
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x ³ |
1 |
|
|
|
|
|
||||||
|
0, |
если |
|
. |
|
|
|
||||||||
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
х=0, х= |
1 |
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
1 - x2 |
, если |
x < 0, |
|
|
|
|||||||||
26. |
|
|
0 < x < 1, |
||||||||||||
f(x)= 1, |
если |
||||||||||||||
|
|
|
x ³ 1. |
|
|
|
|||||||||
|
2x, |
если |
|
|
|
||||||||||
|
х=0, х=1. |
|
|
|
|
|
|
|
|
|
|||||
|
x3 -1, если |
x < 1, |
|
|
|
||||||||||
28. |
|
|
|
|
|
|
1 < x < 2, |
||||||||
f(x)= x -1, |
если |
||||||||||||||
|
|
|
|
|
|
|
x ³ 2. |
|
|
|
|||||
|
- 2, |
если |
|
|
|
||||||||||
|
х=1, х=2. |
|
|
|
|
|
|
|
|
|
|||||
|
x2 -1, если |
x < 0, |
|
|
|
||||||||||
|
|
|
|
|
|
|
x = 0, |
|
|
|
|||||
|
3, |
если |
|
|
|
||||||||||
30. |
f(x)= x -1, |
если |
0 < x < |
1 |
, |
||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
, |
|
|
если |
x ³ |
|
. |
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
х=0, х= 1 . 3
46
Блок 37. Свойства функций, имеющих предел.
1. |
Следует ли из существования предела |
lim [ f (x) + g(x)]=b существование пределов lim f (x) , lim g(x) ? |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x→∞ |
|
|
lim [ f (x) + g(x)]=b |
|
|
|
x |
→∞ |
x→∞ |
|
|||||
2. |
Следует |
ли |
из |
существования |
пределов |
и |
|
lim f (x) =с |
существование предела |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
→+∞ |
|
|
|
x→+∞ |
|
|
|
|
|
||
|
lim g(x) ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
lim [ f (x) × g(x)]=а существование пределов |
|
|
|
|
||||||||||
3. |
Следует ли из существования предела |
lim f (x) , |
lim g(x) ? |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
x |
→+∞ |
x→+∞ |
|
|||
4. |
Известно, что |
lim [ f (x)]2 =b. Следует ли отсюда существование предела |
lim |
f (x) ? |
|
|
|
||||||||||||||||
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
||
5. |
Если lim | f (x) | =b, то что можно сказать о существовании предела lim |
f (x) ? |
|
|
|
|
|
||||||||||||||||
|
x→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→a |
|
|
|
|
|
|
||
6. |
Известно, что |
lim |
f (x) =0 и lim [ f (x) × j(x)]=0. Что в этом случае можно сказать о существовании lim j(x) ? |
||||||||||||||||||||
|
|
|
x→∞ |
|
x→∞ |
|
lim [ f (x) × g(x)] и |
|
|
|
|
|
|
|
|
x→∞ |
|
||||||
7. |
Следует ли из существования пределов |
lim g(x) существование |
lim |
f (x) ? |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x→−∞ |
|
|
x→−∞ |
|
|
|
|
|
x→−∞ |
|
|
|
||
8. |
Следует ли из равенства |
lim [ f (x) + g(x)]=0, что |
lim f (x) =0 и |
lim g(x) =0? |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
x→+∞ |
|
x→+∞ |
|
|
|
|
|
|
||
9. |
Следует ли из равенства |
lim [ f (x) × g(x)]=0, что |
lim f (x) =0 и |
lim |
g(x) =0? |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
x |
→+∞ |
x |
→+∞ |
|
|
|
|
|
|
||
10. |
Известно, что lim [ f (x) × g(x)]=+∞. Что в этом случае можно сказать о существовании lim |
f (x) и lim g(x) ? |
|||||||||||||||||||||
|
|
|
|
x→а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→а |
|
x→а |
|
|
11. |
Известно, что lim[ f (x) + g(x)]=+∞ и |
lim |
f (x) =+∞. Что можно сказать о существовании lim g(x) ? |
|
|||||||||||||||||||
|
|
|
|
x→с |
|
|
|
|
x→с |
|
|
|
|
|
|
|
|
|
x→с |
|
|
||
12. |
Известно, что |
lim [ f (x) - р(x)]=+∞ и |
lim р(x) =+∞. Что в этом случае можно сказать о существовании |
||||||||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
x |
→0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
lim f (x) ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. |
Известно, что lim [p(x) × g(x)]=– ∞. Что в этом случае можно сказать о существовании lim p(x) и lim g(x) ? |
||||||||||||||||||||||
|
|
|
|
x→b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→b |
|
x→b |
|
|
14. |
Может ли хотя бы одна из функций |
|
f(x) или g(x) |
не иметь |
предела |
при х→∞, |
если |
известно, |
что |
||||||||||||||
|
lim [ f (x) × g(x)]=– ∞? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15. |
Известно, что lim [р(x) + k(x)]=0. Можно ли утверждать, что p(x) и k(x) – бесконечно малые при х→а? |
|
|||||||||||||||||||||
|
|
|
|
x→а |
|
lim [a(x) + b(x)]=+∞ существование |
|
|
|
|
|
|
|
|
|||||||||
16. |
Следует ли из существования |
lim a(x) , |
lim b(x) ? |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
x |
→∞ |
|
x→∞ |
|
|
|
|
||
17. |
Следует ли из равенств |
lim [ f (x) + g(x)]=+∞ и |
lim f (x) =+∞, что lim g(x) =+∞? |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x→а |
|
|
|
|
|
|
x→a |
|
|
x→a |
|
|
|
|
|
||
18. |
Известно, что lim [ f (x) × g(x)]=∞. Следует ли отсюда существование lim f (x) , lim g(x) ? |
|
|
||||||||||||||||||||
|
|
|
|
x→а |
|
|
|
|
|
|
|
|
|
|
|
x→а |
x→а |
|
|
|
|
||
19. |
Известно, что lim |
f 2 (x) =+∞. Следует ли отсюда существование lim |
f (x) ? |
|
|
|
|
|
|||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
||
20. |
Если lim | f (x) | =а, то что можно сказать о существовании |
lim f (x) ? |
|
|
|
|
|
|
|||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
21. |
Известно, что |
lim f (x) =∞ |
и |
lim [ f (x) × р(x)]=∞. Что в этом |
случае можно |
сказать о |
существовании |
||||||||||||||||
|
|
|
|
x→∞ |
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim р(x) ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22. |
Следует ли из существования lim [ f (x) × j(x)] и lim j(x) существование lim |
f (x) ? |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
x→0 |
|
|
|
|
x→0 |
|
|
|
|
x→0 |
|
|
|
|
|
||
23. |
Следует ли из равенства lim [k(x) + t(x)]=– ∞, что lim k(x) =– ∞ и lim t(x) =– ∞? |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
x→0 |
|
x→0 |
|
|
|
|
|
|
||
24. |
Известно, что lim [a(x) ×b(x)]=– ∞. Что в этом случае можно сказать о существовании lim a(x) и lim b(x) ? |
|
|||||||||||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
x→0 |
|
|
25. |
Известно, что |
lim [t(x) + р(x)]=– ∞ и |
lim |
р(x) =– ∞. Что можно сказать о существовании |
lim t(x) ? |
|
|||||||||||||||||
|
|
|
|
x→∞ |
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|||
26. |
Известно, что lim [a(x) - b(x)]=– ∞ и lim b(x) =– ∞. Что можно сказать о существовании lim a(x) ? |
|
|||||||||||||||||||||
|
|
|
|
x→a |
|
|
|
x→a |
|
|
|
|
|
|
|
|
|
x→a |
|
|
|||
27. |
Известно, что lim [t(x) × z(x)]=– ∞. Что в этом случае можно сказать о существовании |
lim t(x) и |
lim z(x) ? |
|
|||||||||||||||||||
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
x→∞ |
|
|
28. |
Может |
ли |
хотя |
бы одна из |
функций |
р(х) или g(х) |
не иметь |
предела |
при х→0, |
если |
известно, |
что |
|||||||||||
47
|
lim [p(x) × g(x)]=+∞? |
|
x→0 |
29. |
Известно, что lim [a(x) + b(x)]=∞. Можно ли утверждать, что α(x) |
|
x→∞ |
30. |
Следует ли из существования lim [ f (x) - g(x)]=b существование |
|
x→∞ |
и β(x) – бесконечно большие при х→∞?
lim f (x) , lim g(x) ?
x→∞ x→∞
48
Блок 38. Вычисление предела числовой последовательности (рациональная дробь).
Вычислите предел числовой последовательности:
1. lim
n→∞
3. lim
n→∞
5. lim
n→∞
7. lim
n→∞
9. lim
n→∞
11. lim
n→∞
13. lim
n→∞
15. lim
n→∞
17. lim
n→∞
19. lim
n→∞
21. lim
n→∞
23. lim
n→∞
25. lim
n→∞
27. lim
n→∞
29. lim
n→∞
(3 − n)2 + (3 + n)2 (3 − n)2 − (3 + n)2 .
(6 − n)2 − (6 + n)2 (6 + n)2 − (1 − n)2 .
(3 − n)3
(n + 1)2 − (n + 1)3 .
(n + 3)3 + (n + 4)3 (n + 3)4 − (n + 4)4 .
(2n + 1)2 − (n + 1)2 . n2 + n + 1
(2n + 1)3 − (2n + 3)3 (2n + 1)2 + (2n + 3)2 .
(n + 1)3 − (п −1)3 (n + 1)2 − (n −1)2 .
(3 − n)4 − (2 − п)4 (1 − n)4 − (1 + n)4 .
(n + 1)3 − (n + 1)2 (n − 3)3 − (n + 3)3 .
(n + 1)3 + (n + 2)3 (n + 4)3 + (n + 5)3 .
(n + 6)3 − (n + 1)3 (2n + 3)2 + (n + 4)2 .
(n + 7)3 − (n + 2)3 (3n + 2)3 + (4n + 1)2 .
(n + 1)4 − (n −1)4 (n + 1)3 + (n −1)3 .
(n + 1)3 + (n −1)3 . n3 − 3n
(2n − 3)3 − (n + 5)3 (3n −1)3 + (2n + 3)3 .
2. lim (3 − n)4 − (2 − n)4 . n→∞ (1 − n)3 − (1 + n)3
4. lim (1 + 2n)3 − 8n3 . n→∞ (1 + 2n)2 + 4n2
6.lim 2(n + 1)3 − (n − 2)3 .
→∞ n2 + 2n − 3n
8. |
lim |
|
|
|
|
8n3 |
− 2n |
|
|
|
. |
|
|
|
||||||
|
|
|
|
+ 1)4 |
− (n −1)4 |
|
|
|
|
|||||||||||
|
n→∞ (n |
|
|
|
|
|
|
|
|
|||||||||||
10. |
|
|
|
(n + 2)2 |
− (n − 2)2 |
|
|
|||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||
|
|
|
|
(n |
+ 3)2 |
|
|
|
|
|
|
|
|
|||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|||||||||
12. |
lim |
(n + 2)4 |
− (n − 2)4 |
|
|
. |
|
|
|
|||||||||||
|
|
|
|
|
|
+ (n − |
5)2 |
|
|
|
|
|
||||||||
n→∞ (n + 5)2 |
|
|
|
|
|
|
|
|||||||||||||
14. |
lim |
(n + 2)3 |
+ (n − 2)3 |
|
. |
|
|
|
||||||||||||
|
|
|
|
n4 + 2n2 −1 |
|
|
|
|
|
|||||||||||
n→∞ |
|
|
|
|
|
|
|
|
||||||||||||
16. |
lim |
(1 − n)4 |
− (1 + n)4 |
|
. |
|
|
|
||||||||||||
|
|
|
|
|
− (1 − n)3 |
|
|
|
|
|||||||||||
|
n→∞ (1 + n)3 |
|
|
|
|
|
|
|
|
|||||||||||
18. |
lim |
|
|
|
(3 − 4n)2 |
|
|
|
|
. |
|
|
|
|||||||
|
|
|
− 3)3 |
− (n + |
3)3 |
|
|
|
|
|||||||||||
|
n→∞ (n |
|
|
|
|
|
|
|
||||||||||||
20. |
lim |
(n + 1)4 |
− (п −1)4 |
|
. |
|
|
|
||||||||||||
|
|
|
+ 1)3 |
+ (n −1)3 |
|
|
|
|
||||||||||||
|
n→∞ (n |
|
|
|
|
|
|
|
|
|||||||||||
22. |
lim |
(n + 10)2 + (3п + 1)2 |
. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n→∞ (n + 6)3 − (n + 1)3 |
|
|
|||||||||||||||||
24. |
lim |
|
n3 |
− (п −1)3 |
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
+ 1)4 |
− n4 |
|
|
|
|
|
|
|
|
|
|||||||
|
n→∞ (n |
|
|
|
|
|
|
|
|
|
|
|||||||||
26. |
lim |
(n + 1)3 |
− (п −1)3 |
. |
|
|
|
|||||||||||||
|
|
+ 1)2 |
+ (n −1)2 |
|
|
|
||||||||||||||
|
n→∞ (n |
|
|
|
|
|
|
|
||||||||||||
28. |
lim |
(n + 1)3 |
+ (п −1)3 |
|
. |
|
|
|
||||||||||||
|
|
n3 + 1 |
|
|
|
|
|
|
||||||||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|||||||||
30. |
lim |
(2n + 1)3 + (3п + 2)3 |
. |
|||||||||||||||||
|
|
|
|
|
|
7)3 |
|
|||||||||||||
|
n→∞ (2n + 3)3 − (n − |
|
|
|||||||||||||||||
49
Блок 39. Вычисление предела числовой последовательности (иррациональное выражение)
Вычислите предел числовой последовательности:
1. |
|
n3 5n2 + 4 9n3 +1 |
||||||||||||
lim |
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
||||||||||||
|
n→∞ |
(n + |
n |
) 7 - n + n2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
- 5 125n3 + n |
|||||||||
3. |
|
|
3n -1 |
|||||||||||
lim |
|
|
|
. |
||||||||||
|
|
|
|
|||||||||||
|
n→∞ |
|
|
5 n + n |
||||||||||
5.lim 6n3 - 
n5 +1 .
→∞ 
4n6 + 3 - nn
7.lim 
n5 + 3 - 
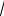n - 3 .
→∞ 5
n5 + 3 + 
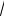n - 3n
9. |
|
|
3 n3 - 7 + |
3 n2 + 4 |
||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
n→∞ |
|
4 n5 + 5 + |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
n × 4 |
|
|
|
|
|
|
|
|
|
+ 25n4 - 81 |
|||||||||||||||||||||||||
11. |
|
|
11n |
|||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
n→∞ |
(n - 7 |
|
n |
|
) n2 - n +1 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
- 3 n3 + 2 |
|||||||||||||||||||||||||||
13. |
|
|
|
n + 2 |
||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n→∞ |
7 |
n + 2 |
- 5 n5 + 2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
n2 +1 |
|||||||||||||||||||||
15. |
|
|
|
|
n -1 |
|
||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n→∞ |
3 3n3 + 3 + 4 n5 +1 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
n × 5 |
|
|
- 3 27n6 + n2 |
||||||||||||||||||||||||||||||||
17. |
lim |
|
n |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
n→∞ |
|
(n + 4 |
n |
) 9 + n2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
3 8n3 + 5 |
|||||||||||||||||||||
19. |
|
|
|
5n + 2 |
||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
n→∞ |
|
|
|
|
4 n + 7 - n |
||||||||||||||||||||||||||||||||
3n - 9n2
21.lim 
. →∞ 3n - 4 9n8 +1n
23. |
lim |
|
|
n6 + 4 + |
|
|
n - 4 |
|
. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
n→∞ |
6 n6 + 6 - |
n - 6 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
25. |
|
|
3 n2 - |
|
n2 + 5 |
|||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n→∞ |
5 n7 - |
|
n +1 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
n |
|
|
|
|
|
- |
|
64n6 + 9 |
|
||||||||||||||||
27. |
|
|
71n |
|||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
n→∞ |
(n - 3 |
n |
) 11 + n2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
- 3 n3 +1 |
|||||||||||||||||
29. |
|
|
|
n +1 |
||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
n→∞ |
4 |
n +1 |
- 5 n5 +1 |
||||||||||||||||||||||||
2.lim 
n3 +1 - 
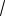n -1 .
→∞ 3
n3 +1 - 
n -1n
4. |
|
|
|
n + 2 |
- |
n2 + 2 |
|||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n→∞ |
4n |
4 |
+1 |
- |
|
n |
4 |
-1 |
|
|||
|
|
|
|
|
|
|
|||||||
6.lim n × 4
3n +1 + 
81n4 - n2 +1 .
→∞ (n + 3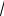
n )
5 - n + n2n
8. lim 
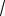4n +1 - 
27n3 + 4 .
n→∞ 4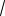
n - 3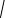
n5 + n
4n2 - 4 n3
10. lim 
.
n→∞ 3 n6 + n3 +1 - 5n
12. |
lim |
|
|
|
n7 |
+ 5 - |
|
|
|
n - 5 |
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n→∞ 7 n7 + 5 + |
n - 5 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
- |
|
n2 - 6 |
|
|||||||||||
14. |
|
|
|
|
n + 6 |
|
||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n→∞ 3 |
|
n |
3 |
+ 3 - |
4 |
|
n |
3 |
+1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 n2 -1 + 7n3
16. lim 
.
n→∞ 4 n12 + n +1 - n
18. lim 
n4 + 2 + 
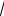n - 2 . n→∞ 4
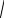n4 + 2 + 
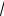n - 2
20. lim 
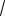n + 3 - 
n2 - 3 .
n→∞ 3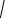
n5 - 4 - 4
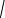n4 +1
22. lim n ×3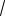
7n - 4
81n8 -1 . n→∞ (n + 4
n )
n2 - 5
24. lim 
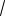n + 3 - 3
8n3 + 3 .
n→∞ 4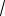
n + 4 - 5
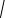n5 + 5
3n2 + 2 - 5n2
26.lim 
. n→∞ n - 
n4 - n +1
28.lim 
n8 + 6 - 
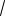n - 6 .
→∞ 8
n8 + 6 + 
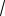n - 6n
30. lim n × 6
n + 5
32n10 +1 . n→∞ (n + 4
n ) × 3
n3 -1
50