
SBORNIK_PO_MATANU_ShKERINA_mIKhALKIN
.pdf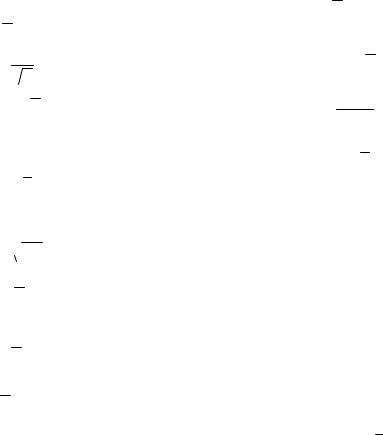
Блок 15. Непериодические функции.
Докажите, что функция не является периодической:
1. f(x)=х2.
3. f(x)= 
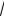 х .
х .
5. f(x)=sin 1 .
 х
х
7. f(x)=sin ( 
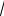 х )2.
х )2.
9. f(x)=x + cos x.
11. f(x)=x + sin x. 13. f(x)= 3sin 
 x . 15. f(x)=x×cos x. 17. f(x)=x×tg x.
x . 15. f(x)=x×cos x. 17. f(x)=x×tg x.
19. f(x)=sin 
 | х | .
| х | .
21. f(x)=cos 1 .
х
23. f(x)=tg x2.
25. f(x)=sin 1 .
х
1 sin|x|
27. f(x)= .
2
29. f(x)=3x + sin x.
2. f(x)= 1 .
х
4.f(x)=x2+x+1.
6.f(x)=cos 
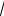 х .
х .
1
8. f(x)= х3 +1 .
10.f(x)=sign x.
12.f(x)=tg 
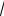 х .
х .
14.f(x)=x – tg x.
16.f(x)=x×sin x.
18.f(x)=sin |x|.
20.f(x)=sin x2.
22.f(x)=cos x2.
24.f(x)=ctg x2.
26.f (x)= 2sin x2 .
28.f(x)=2x×cos x.
cos 1
30. f(x)= 0,5 x .
21

Блок 16. Продолжение функции по периоду.
Функцию f продолжить периодически на всю числовую ось с наименьшим положительным периодом Т:
1. |
f(x)=x2+x+1, 0£x<4, T=4. |
2. |
f(x)=|x2–3 x+2|, 0£x£3, T=3. |
||||||
3. |
f(x)=x2–2 x, |
0£x<3, |
T=3. |
4. |
f(x)=|3x– x2–2|, |
0,5 £x<3, T=2,5. |
|||
5. |
f(x)= |
1 |
, –2 £x£2, |
x¹0, T=4. |
6. |
f(x)=3x– x2–2, |
1 £x£2, T=1. |
||
2 |
|||||||||
|
|
х |
|
|
|
1 - x, |
|
|
|
7. |
f(x)=2x– x2, |
0£x<3, |
T=3. |
8. |
если 0 £ х < 1, |
||||
f(x)= |
|
T=10. |
|||||||
|
|
|
|
|
|
|
lg x, |
если 1 £ х £ 10. |
|
|
|
1 |
|
если 1 £ х £ 2, |
|
|
|
||
9. |
|
|
, |
T=3,5. |
|||||
|
|||||||||
f(x)= |
х |
|
|
|
|||||
|
|
|
|
если 2 < x £ 4,5. |
|
|
|
||
|
1, |
|
|
|
|||||
11. |
|
- х, |
если – 2 £ x < 0, |
T=3.12. |
|||||
f(x)= |
|
если 0 £ x < 1. |
|||||||
|
|
-1, |
|
|
|||||
13. |
|
lg x, если 1 £ x < 10, |
T=9. 14. |
||||||
f(x)= |
|
если x = 10. |
|
||||||
|
|
0, |
|
|
|
|
|||
|
|
|
|
π |
£ x |
< 0, |
|
5π |
|
15. |
|
tg x, |
если – |
|
|||||
f(x)= |
|
4 |
|
|
T= |
|
|||
|
|
|
|
||||||
|
|
|
|
если 0 £ x £ |
π . |
4 |
|||
|
|
- 1, |
|
|
|||||
|
x, |
если 0 £ x < 1, |
|
10. f(x)= |
- x, |
если 1 £ x £ |
T=2. |
2 |
2. |
||
|
|
|
||
cos x, |
||||
f(x)= |
|
|
||
|
|
|
||
1, |
|
|
||
|
|
|
||
|
|
x |
||
1 |
|
|||
|
|
|
, |
|
|
||||
f(x)= 2 |
|
|
||
|
+ x, |
|||
-1 |
||||
если 0 £ x £ π ,
2 T=p.
если π < x £ π . 2
если 0 £ x < 1,
T=2.
если 1 £ x £ 2.
. 16. |
| x |, |
если – 1 £ x £ 1, |
|
f(x)= |
если 1 < x £ |
T=3. |
|
|
1, |
2. |
|
|
|
|
|
|
|
|
|
3 |
, |
|
– 1 £ x £ |
1 |
, |
||
|
log1/ 2 x, если 1 £ x < 2, |
|
|
|
x |
|
если |
|
|||||||
|
|
|
|
|
2 |
||||||||||
17. |
|
|
|
|
|
|
|
|
|
|
T=2. |
||||
f(x)= |
|
если 2 £ x < 3. |
T=2. 18. f(x)= |
|
|
|
1 |
|
|
||||||
|
-1, |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
-1, |
если |
|
|
< x £ 1. |
|
|||
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x, |
если – 1 £ x £ 0, |
|
x, |
|
|
|
если |
0 £ x < 1, |
|
|
||||
19. |
|
|
|
|
|
|
|
|
|
|
|
T=2. |
|||
f (x)= |
- x, |
T=2. 20. |
f(x)= |
|
|
|
|
|
|
|
|
|
|||
|
|
если 0 < x £ 1. |
|
|
2 |
- 4, |
если |
1 £ x £ 2. |
|
|
|||||
|
|
|
|
x |
|
|
|
||||||||
21. |
0, |
если – π £ x < 0, |
|
||||||
f(x)= |
|
|
|
0 £ x < π . |
|
|
|||
|
sin x, |
если |
|
|
|||||
|
|
|
|
|
|
π |
£ x < |
π |
|
23. |
sin x, |
если |
– |
2 |
2 |
, |
|||
f(x)= |
|
|
|
|
π |
|
|
|
|
|
|
|
|
если |
|
£ x £ π . |
|
||
|
|
|
|
|
|
||||
|
- 1, |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
£ x £ |
π |
|
25. |
cos x, |
|
если |
– |
2 |
2 |
, |
||
f(x)= |
|
|
|
|
π < x £ π . |
|
|||
|
sin x, |
|
если |
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 - x |
2 |
, если – 1 £ x £ 1, |
||||||
27. |
|
|
|||||||
f(x)= |
|
|
|
|
|
|
|
|
|
|
|
- 2, |
|
если |
1 < x £ 2. |
||||
|
x |
|
|||||||
|
1, |
если – 1,5 £ x < -1, |
|
||||||
29. |
|
|
|
|
|
|
|
|
|
f(x)= | x |, если – 1 £ x £ 1, |
|
|
|||||||
|
|
если |
1 < x £ 1,5. |
|
|||||
|
1, |
|
|||||||
|
|
|
|
|
|
1 - x |
2 |
, |
|
|
|
|
|
|
|
|
|||
T=2p. 22. f(x)= |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x -1, |
|
|
|
|
|
3π |
|
|
|
|
|
|||
|
|
|
. 24. |
|
ctg x, |
||||
T= |
|
|
f(x)= |
|
|
|
|||
|
|
|
|
|
|||||
|
2 |
|
|
|
0, |
|
|
|
|
|
|
3π |
|
- x2 |
, |
||||
|
|
|
|
|
|
|
|||
T= |
|
|
. 26. |
f(x)= |
|
|
|
||
|
|
|
|
||||||
|
2 |
|
|
|
- 4, |
|
|
||
|
|
|
|
|
|
|
|
|
|
если
если
если
если
если
если
0 £ x £ 1, T=2.
1 < x £ 2.
0 < x < π ,
T=p.
x = 0, x = π .
– 2 £ x £ 0,
0 < x £ 1 . T=2,5.
2
|
-1, |
если – |
2 £ x £ -1, |
|
|
T=3. 28. |
|
если – 1 |
< x < 1, |
T=4. |
|
f(x)= x, |
|||||
|
|
если |
1 |
£ x £ 2. |
|
|
-1, |
|
|||
2− x |
, |
если – |
2 £ x < -1, |
|
|
|
если – 1 £ x £ 0, |
|
|
T=3. 30. f(x)= 2, |
|
T=4. |
||
|
|
|
0 < x £ 2. |
|
2 + x, |
если |
|
||
22
Блок 17. Свойства периодических функций.
1.Приведите пример периодической функции, являющейся суммой (разностью) двух периодических функций.
2.Может ли периодическая функция иметь обратную?
3.Может ли убывающая (возрастающая) на всей числовой прямой функция быть периодической?
4.Докажите, что если Т1 и Т2 – периоды функции f, то числа Т1+Т2 и Т1– Т2 (при Т1¹Т2) являются периодами этой функции.
5.Убедитесь, что функция у=с является периодической и ее периодом является любое действительное число. Имеет ли эта функция наименьший положительный период?
6.Приведите пример функции с периодом 2; с периодом 5.
7.Докажите предложение: если f – периодическая функция, то какова бы ни была функция g, композиция функций f и g является периодической функцией.
8.Пусть h – периодическая функция, а g – непериодическая. Является ли периодической композиция функций h и g?
9.Являются ли периодическими функциями: а) сумма двух периодических функций; б) произведение двух периодических функций? Докажите и приведите примеры.
10.Пусть f – периодическая функция, kÎR, k¹0. Являются ли периодическими функции:
а) g(x)=f k(x); б) р(х)=f(xk)?
11. Пусть f – периодическая функция, kÎR, k¹0. Являются ли периодическими функции:
а) g(x)=f (x+k); б) р(х)=kf(x)?
12.Приведите примеры непериодических функций f и g таких, что функции f +g и f×g – периодические и имеют наименьший положительный период.
13.Функция g обратна самой себе и определена композиция g f . Пусть существует Т¹0 такое, что для
|
любого хÎD(f) выполняются условия |
х+ТÎD(f), х– ТÎD(f) и |
f(х+Т)=g(f(x)). Докажите, что f – |
||||||||
|
периодическая функция и найдите ее период. |
|
|
|
|
|
|
|
|||
14. |
Докажите, что функция f является периодической, если существует Т¹0 такое, что для любого хÎD(f), |
||||||||||
|
х+ТÎD(f), х– ТÎD(f), и выполнено одно из условий: |
f (x) + a |
|
|
|
|
|
||||
|
1) f(x+T) = – f(x); |
2)f(x+T) = |
1 |
; |
3)f(x+T) = |
. Найдите период функции f. |
|||||
|
f (x) |
|
|||||||||
|
|
|
|
|
bf (x) -1 |
|
|
− f (x) |
|
||
15. |
Докажите, что если при любом значении х имеет место равенство |
f(x+с) = |
1 |
, где с – постоянное |
|||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
+ f (x) |
||
|
число, то функция f |
– периодическая. |
|
|
|
|
|
|
|
|
|
16.Пусть |f(x)| – периодическая функция. Следует ли отсюда, что f(x) – периодическая функция?
17.Всякая ли периодическая функция обязательно четная или нечетная?
18.Докажите, что функция Дирихле является периодической, но не имеет наименьшего положительного периода.
19.Справедливо ли утверждение, что всякий многочлен и отношение двух многочленов являются непериодическими функциями?
20.Пусть функция f является периодической. Верны ли высказывания: а) p(x)= |f(x)| – периодическая функция; б) g(x)= f(|x|) – периодическая функция?
21.Докажите, что если отношение периодов периодических функций f и g является рациональным
числом, то функции f +g и f×g периодичны.
22.Докажите, что если l является периодом функции y=f(x), xÎ(-¥;+¥), то числа ±nl (nÎN) также являются периодами этой функции.
23.Выведите правило отыскания наименьшего положительного периода для функции:
а) f(x)=sin (kx+b); б) g(x)=cos (nx+c); в) j(x)=tg (mx+d).
24.Приведите примеры периодической функции f и непериодической функции g таких, что f×g – периодическая функция и имеет наименьший положительный период.
25.Докажите, что сумма и произведение двух периодических функций, определенных на одном и том же множестве и имеющих кратные периоды, есть также периодические функции.
26.При каких a и b (ab¹0) функция у=ах– Е(bx+c) – периодическая и каков ее наименьший положительный период?
27.Существует ли функция, для которой каждое рациональное число является периодом, а каждое иррациональное – нет?
28.Докажите, что любое число, отличное от нуля, может быть периодом некоторой функции. (Рассмотрите функцию y=sin kx.)
29.График функции y=f(x), xÎR, симметричен относительно каждой из прямых х=а и х=b (а¹b). Докажите,
23
что y=f(x) – периодическая функция, и найдите ее период.
30. График функции y=f(x), xÎR, симметричен относительно точки А(а;b) и прямой х=с (с¹а). Докажите, что y=f(x) – периодическая функция, и найдите ее период.
24
Блок 18. Исследование функции на четность и нечетность.
Исследуйте на четность и нечетность следующие функции:
|
2 |
|
а |
х -1 |
|
1. |
а) f(x)=(1– x )×cos x; |
б) f(x)=х× |
|
|
. |
|
|
||||
2.а) f(x)=(1+cos x)×ctg x;
3.а) f(x)= х ;
sin x
4. а) f(x)= sin x ; | sin x |
5.а) f(x)=10х + 10– х;
6.а) f(x)= 1 + cos x ;
1- cos x
7.а) f(x)=lg cos x;
8.а) f(x)=2sin x;
9.а) f(x)=sin х×cos 2x;
10.а) f(x)=sin (cos 2х);
11.а) f(x)= 
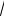 1 + х +
1 + х + 
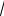 1 - х ;
1 - х ;
1
12. а) f(x)=  ;
;  1 - х2
1 - х2
13.а) f(x)=21+cos х ;
x+ 1
14.а) f(x)= 1 + x2 ;
15.а) f(x)= 1 + sin x ;
sin x
16.а) f(x)=sin х + cos x;
17.а) f(x)= a x + a− x ;
2
18.а) f(x)=х2+|x+1|;
19.а) f(x)= a x - a− x ;
|
|
|
|
2 |
|
|
|
|
20. а) |
f(x)=lg |
1 + х |
; хÎ(–1;1); |
|||||
|
|
|
||||||
|
|
|
1 - х |
|||||
21. а) |
|
a x |
+1 |
|
||||
f(x)= |
|
|
|
|
; |
|||
a x |
|
|
|
|||||
|
|
-1 |
|
|||||
22. а) |
f(x)= 2x− x4 |
; |
|
|||||
23. а) |
f(x)=sin2 5x + cos 3x; |
|||||||
24. а) |
|
х2 |
+1 |
|
||||
f(x)= |
|
|
|
; |
||||
х2 |
|
|
||||||
|
|
-1 |
|
|||||
б) f(x)=х– х3 + х5 .
|
|
6 |
120 |
|
|
|||||
б) |
f(x)= |
1 - 22kx |
|
. |
|
|
|
|||
1 + 22kx |
|
|
|
|||||||
|
|
|
|
|
|
|||||
б) |
f(x)=6х2+8+(х–2) 3. |
|||||||||
б) |
f(x)= |
| sin x | |
. |
|
|
|||||
|
|
|
||||||||
|
|
1 - cos x |
|
|
|
|
||||
б) |
f(x)=ln |
1 − x |
. |
|
|
|
|
|||
1 + x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
б) f(x)= 3 (1 - х)2 + (1 + х)2 . |
||||||||||
б) f(x)= 
 1 + х + х2 -
1 + х + х2 - 
 1 - х + х2 .
1 - х + х2 .
б) |
|
1 + x |
2 |
|
f(x)= lg x + |
|
. |
||
|
|
|
|
|
б) f(x)= 5 (х -1)2 + 5
(х -1)2 + 5 (х +1)2 .
(х +1)2 .
б) |
f(x)=sin |
2 |
– е |
− х2 |
|
|
|
|||||||||||
х |
|
. |
|
|
|
|
||||||||||||
б) |
f(x)=ln |
2 + х |
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 - х |
|
|
|
|
|
|
|
|
|||||
б) |
f(x)= |
cos x3 + 7x12 |
. |
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
x6 + sin2 x3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
|
|
|
|
2 |
+ |
|
1 + x |
2 |
|||||||||
f(x)=ln x |
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
f(x)= |
|
2x + 2− x |
|
. |
|
|
|
|
|
||||||||
|
x |
|
|
− x |
|
|
|
|
||||||||||
|
3 |
|
|
- 3 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
б) |
f(x)=ln |
|
x |
2 |
+1 + 3 |
|||||||||||||
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
f(x)=tg х3 + 4x9. |
|
|
|
||||||||||||||
б) f(x)= 
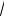 х - 2 +
х - 2 + 
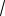 х + 2 .
х + 2 .
б) f(x)= 
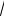 1 - х +
1 - х + 
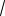 1 + х .
1 + х .
б) f(x)=cos (sin 3x).
б) f(x)= 3 (1 + x)2 +
(1 + x)2 + 
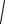 (1 - x)2 .
(1 - x)2 .
б) |
f(x)= |
|
| x -1 | |
+ |
| x +1 | |
. |
|
б) |
f(x)= |
|
х |
. |
|||
|
|
||||||
|
|
а |
х -1 |
||||
б) |
f(x)= |
2sin 2 x− x . |
|||||
25

25. а) |
f(x)= |
|
x3 + x2 - 8 ; |
|
|
|
|
||||||||
26. а) |
f(x)= |
x2 + x -1 |
; |
|
|
|
|
|
|||||||
|
x3 - 5 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
27. а) |
f(x)=ln |
1 − х |
; |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 + х |
|
|
|
|
|
|
|
|
|
|
||
28. а) |
f(x)=sin x + 2x3; |
|
|
|
|
||||||||||
|
|
|
1 + |
х |
2 |
|
|
|
|
2 |
|||||
|
|
|
|
|
|
1 |
|
|
|||||||
29. а) |
f(x)= |
1 - |
|
|
|
|
|
|
|
+ |
|
|
; |
||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 + х |
|
|
|
1 - х |
|||||||
|
|
|
|
|
х |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
30. а) |
f(x)=(х–1) 2×sin2 x; |
|
|
|
|
||||||||||
б)
б)
б)
б)
б)
б)
3− x + 3x f(x)= 2x - 2− x .
f(x)=x2 – |sin x| + cos x.
10х +1 f(x)= 10х -1 .
f(x)=ln |(x–1)(1+ x)|.
f(x)= 
 х2 - х + 3 +
х2 - х + 3 + 
 х2 + 2х + 2 .
х2 + 2х + 2 .
1 + 2kx f(x)= 1 - 2kx .
26

Блок 19. Четное и нечетное продолжение функции.
Продолжите на всю числовую прямую каждую из следующих функций четным и нечетным образом. Постройте графики данных и полученных функций.
1. |
f(x)=x, x [–4;0]. |
2. |
f(x)=x2, x [–2;0]. |
||
3. |
f(x)=x3, x [0;1]. |
4. |
f(x)=x–1, |
x [1;3]. |
|
5. |
f(x)= – x2, |
x [0;2]. |
6. |
f(x)=x2+2, x [–2;0]. |
|
7. |
f(x)=1– x, |
x [–3;–1]. |
8. |
f(x)=4– x2, |
x [1;2]. |
|
π |
3π |
|
9. f(x)=sin x, x |
; |
|
. |
|
|||
|
2 |
2 |
|
11. |
f(x)= –sin x, |
x [0;π]. |
13. |
f(x)=|cos x|, |
x [– π;0]. |
15. |
f(x)=cos x – 1, x [0;π]. |
|
10.f(x)=cos x, x π ; 3π .
2 2
|
π |
3π |
|
12. f(x)=|sin x|, x |
; |
|
. |
|
|||
|
2 |
2 |
|
14. |
|
x |
|
π |
|
||
f(x)=sin x – 1, |
|
|
|
; π . |
|||
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
π |
|
|
16. |
f(x)= –cos x, |
x − |
|
|
|
;0 . |
|
|
|
|
|||||
|
|
|
|
2 |
|
||
17. |
f(x)= |
1 − х |
, |
|
x(0;1]. |
|||
19. |
f(x)=2x, x(0;1]. |
|
||||||
21. |
f(x)=x3–1, |
x [–2;–1]. |
||||||
23. |
f(x)=(x–1) 3, |
x[1;3]. |
||||||
25. |
f(x)=x– x2, |
x [0;2]. |
||||||
27. |
f(x)=x– x2+6, |
|
x(0;3]. |
|||||
29. |
|
|
|
|
|
π |
|
|
f(x)=cos х + |
|
, |
x − |
|||||
|
|
|
|
|
|
6 |
|
|
π;− π . 6
18.f(x)=lg x, x[0;10].
20.f(x)=2x–1, x[–1;0 ].
22.f(x)=(x+1)3, x[–2;0).
24.f(x)=x2– x, x[0;2].
26. |
f(x)=x2– x–6, |
x[–2;0). |
|
|
|
|
|
|
|
|
π |
|
π 4π |
||||
28. |
f(x)=sin х − |
, |
x |
; |
|
|
. |
|
|
|
|||||||
|
|
3 |
|
3 3 |
|
|
||
|
|
π |
|
|
5π |
|||
30. |
f(x)=sin х + |
, |
x |
0; |
|
|
. |
|
|
|
|||||||
|
|
4 |
|
4 |
|
|||
27

Блок 20. Свойства четных и нечетных функций.
1.Что можно сказать о четности функции | f |, если известно, что функция f : а) четная; б) нечетная? Может ли монотонная на всей числовой прямой функция быть: а) четной; б) нечетной?
2.Может ли функция быть одновременно и четной и нечетной?
3.Может ли функция, обратная к данной, быть четной?
4.Покажите, что если функция f определена для всех действительных значений аргумента х, то функция f(x)+f(– x) – четная, а функция f(x)– f(– x) – нечетная.
5.Четной или нечетной является сумма (разность): а) двух четных функций; б) двух нечетных функций?
6.Докажите, что: а) произведение двух четных или нечетных функций есть функция четная; б) произведение четной и нечетной функций является функцией нечетной.
7.Докажите, что четная монотонная функция является постоянной.
8.Докажите, что функция, обратная нечетной, также нечетна.
9.Всякая ли нечетная функция имеет обратную? Приведите примеры.
10.Может ли четная функция, определенная на некотором промежутке, иметь обратную?
11.Докажите, что график четной функции симметричен относительно оси ординат, а график нечетной – относительно начала координат.
12.Докажите, что функция f(j(t)), где j(t) – четная функция, четна.
13.Докажите, что если у=f(x) и х=j(t) – нечетные функции, то функция у=f(j(t)) – четная.
14. |
Докажите, что если у=f(x) – четная функция, а х=j(t) – нечетная, то функция у=f(j(t)) – четная. |
|||
15. |
Существуют ли функции, имеющие симметричную относительно нуля область определения и |
|||
|
являющиеся: |
|
|
|
|
а) четными (нечетными) и убывающими; |
б) нечетными (четными) и возрастающими; |
||
|
в) четными (нечетными) и положительными? |
Приведите примеры. |
||
16. |
Существуют ли функции, имеющие симметричную относительно нуля область определения и |
|||
|
являющиеся: |
|
|
|
|
а) четными (нечетными) и неположительными; |
б) нечетными и постоянными; |
||
|
в) четными и постоянными? |
Приведите примеры. |
|
|
17.Может ли иметь четное число экстремумов: а) четная функция; б) нечетная функция? Приведите примеры.
18.Сформулируйте достаточные условия четности и нечетности а) линейной функции;
б) квадратичной функции.
19.Сформулируйте достаточные условия четности и нечетности функции f(x)=ax3+bx2+cx+d, а¹0.
20.Сформулируйте достаточные условия четности или нечетности функции f(x)= ax + b , с¹0.
+d
21. Известно, что f – четная, а g – нечетная функции. Исследуйте на четность и нечетность композиции f g и g f .
22.Функция f – ни четная, ни нечетная, функция g – четная. Может ли сумма f+g быть: а) четной; б) нечетной?
23.Функция f – ни четная, ни нечетная, функция h – нечетная. Может ли сумма f+h быть: а) четной; б) нечетной?
24.Функция f – ни четная, ни нечетная, функция g – четная, функция h – нечетная, и имеет смысл композиция любых двух из этих функций. Укажите все композиции, являющиеся четными функциями.
25.Функция f – ни четная, ни нечетная, функция g – четная, функция h – нечетная, и имеет смысл композиция любых двух из этих функций. Укажите все композиции, являющиеся нечетными функциями.
26.Покажите, что если четная функция f, определенная на множестве всех действительных чисел, в
интервале (0;+¥) возрастает (убывает), то в интервале (– ¥;0) она убывает (возрастает).
27.Покажите, что если нечетная функция f, определенная на множестве всех действительных чисел, в интервале (0;+¥) возрастает (убывает), то в интервале (– ¥;0) она также возрастает (убывает).
28.Покажите, что любую функцию f, определенную на симметричном относительно нуля множестве,
можно представить в виде суммы четной функции j и нечетной функции g. |
|
||||
29. Почему нельзя представить в виде суммы четной и нечетной функции следующие функции: |
а) |
||||
|
|
1 |
|
|
|
|
|
|
|||
f(x)= |
x ; б) f(x)=lg x; в) f(x)=tg (x–5); г) f(x)= |
|
? |
|
|
x +1 |
|
||||
28

Блок 21. Промежутки монотонности.
Докажите, что указанный промежуток является промежутком монотонности для данной функции.
1. |
у=ах, |
0<a<1, (– ∞;+∞). |
2. |
y=cos x, |
[0;π]. |
|
|||
3. |
y=а |
х |
, |
a>1, (– ∞;+∞). |
4. |
y=sin x, |
|
π |
π |
|
− |
; |
. |
||||||
|
|
|
|
|
|
|
|
2 |
2 |
5. |
y=(1– х2), |
[0;+∞). |
6. |
y=x3, (– ∞;+∞). |
|
|||||||||||||||||||||||||||
7. |
y=2 |
sin x |
, |
|
|
|
|
|
|
|
|
π |
|
8. |
2 |
|
|
|
|
|
[1;+∞). |
|||||||||||
|
|
|
|
|
|
|
|
|
0; |
. |
y=x –2 x+6, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
9. y=|x2+4x+3|, |
|
|
[–1;+ ∞). |
10. |
y=5–4 x–x 2, |
(– ∞;–5). |
||||||||||||||||||||||||||
11. |
y= |
|
π |
− х |
|
, |
|
|
π |
|
12. |
|
|
2 |
– x), |
(1;+∞). |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
;+∞ . |
y=lg (x |
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
π |
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
(– ∞;0). |
|
|
|
|
2 |
|
|
||||||||||
13. |
y=log1/2 (x |
|
– x), |
14. |
y=1– |
|
|
|
|
, |
0; |
. |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
2 |
|
||||
15. |
|
|
ctg x |
|
|
π π |
16. |
|
|
3 |
|
|
π |
|
||||||||||||||||||
y= |
|
|
|
|
|
|
|
|
, |
|
|
; |
. |
y=cos |
|
x, 0; |
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
2 |
|
|
||||||||
|
Докажите, что функция: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
17. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
f(x)= 2 х убывает на каждом интервале, не содержащем нуля. |
|
|
||||||||||||||||||||||||||||||
18. |
f(x)=х3+х2 возрастает на промежутке (0;+∞). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
19. |
f(x)= |
1 + х |
2 |
|
|
строго возрастает на промежутке [1;+∞). |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
20. |
f(x)= |
|
1 + х2 |
|
|
строго убывает на промежутке (0;1). |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21. |
f(x)= |
1 + х |
2 |
|
|
строго возрастает на промежутке (– ∞;–1]. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
22. |
f(x)= |
|
1 + х2 |
|
|
строго убывает на промежутке [–1;0). |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23. |
f(x)= |
|
1 − х2 |
|
|
убывает на каждом интервале, не содержащем нуля. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24. |
f(x)= |
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
убывает на промежутке (1;+∞). |
|
|
|
|
|
|
|
|
|
|||||
|
1 + х2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
25. |
f(x)=х3+х |
|
возрастает на промежутке (– ∞;+∞). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
26. |
f(x)= |
|
|
|
|
1 − х2 возрастает на промежутке (–1;0). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
27. |
f(x)= |
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
возрастает на промежутке (– ∞;+∞). |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 + х2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
28.f(x)=log3 (х2–2 х) убывает на промежутке (– ∞;0).
29.f(x)=log3 (х2–2 х) возрастает на промежутке (2;+∞).
30.f(x)=х3+х2 монотонна на промежутке [–1;0].
29

Блок 22. Свойства монотонных функций.
1.Докажите, что сумма двух убывающих функций f и g (D(f)=D(g)) есть убывающая функция.
2.Приведите примеры, показывающие, что разность двух возрастающих функций может быть: а) возрастающей; б) убывающей; в) немонотонной.
3.Докажите, что сумма двух возрастающих функций f и g (D(f)=D(g)) есть возрастающая функция.
Функция f является возрастающей и D(f)=R. Может ли функция f быть:
4.Всюду положительной?
5.Всюду отрицательной?
6.Положительной на некотором промежутке и отрицательной на его дополнении?
7.Функция f возрастает на промежутках [0;2) и (2;3]. Можно ли утверждать, что в этом случае функция f возрастает на [0;3]?
8.Может ли произведение двух убывающих функций быть: а) возрастающей функцией; б) немонотонной функцией?
9.Приведите примеры, показывающие, что разность двух убывающих функций может быть: а) убывающей; б) возрастающей; в) немонотонной.
10.Приведите пример двух возрастающих функций, произведение которых может быть: а) возрастающей функцией; б) немонотонной функцией.
11.Может ли произведение двух возрастающих функций быть функцией убывающей?
12.Докажите, что: а) если функция f возрастает, то функция – f убывает; б) если функция f>0 и
возрастает, то 1 убывает. f
13.Приведите пример функции, определенной на R, которая не является монотонной ни на одном интервале.
14.Приведите пример двух убывающих функций, произведение которых является также функцией убывающей.
15.Приведите примеры, показывающие, что функция, являющаяся суммой двух немонотонных функций, может быть функцией возрастающей.
16.Приведите примеры, показывающие, что функция, являющаяся суммой двух немонотонных функций, может быть функцией убывающей.
17.Докажите, что сумма возрастающей и убывающей функций может быть: а) возрастающей функцией; б) убывающей функцией.
18.Докажите, что произведение возрастающей функции на убывающую может быть: а) возрастающей функцией; б) убывающей функцией.
19.Может ли нечетная функция в своей области определения быть убывающей?
20.Может ли четная функция в своей области определения быть убывающей?
21.Может ли нечетная функция в своей области определения быть возрастающей?
22.Может ли четная функция в своей области определения быть возрастающей?
23.Докажите, что если функции f и g возрастают и положительны на некотором промежутке, то их композиция f g также возрастает и положительна на этом промежутке.
24.Докажите, что композиция двух возрастающих функций есть функция возрастающая.
25.Докажите, что если функция y=F(x) возрастает на [f(β);f(α)], функция x=f(t) убывает на [α;β], то
y=F(f(t)) убывает на [α;β].
26. Известно, что f – возрастающая, а g – убывающая функции. Исследуйте на возрастание композицию f g .
27. Известно, что f – возрастающая, а g – убывающая функции. Исследуйте на возрастание композицию g f .
28.Докажите, что функция, обратная к возрастающей функции, является возрастающей.
29.Докажите, что функция, обратная к убывающей функции, является убывающей.
30.Известно, что функция f убывает, а функция g – возрастает. Исследуйте на возрастание (убывание) композиции f g и g f .
30
