1)конечным и обозримым, так что мы можем устанмвить свойства и отношения каждого элемента этого множества;

2)конечным, но не обозримым, так, что мы не можем установить свойства или отношения каждого элемента этого множества, и, наконец,

3)бесконечным.

Если мы хотим иметь знание о свойствах или отношениях элементов множеств двух последних видов, то возникает проблемная ситуация: мы можем наблюдать только конечное ограниченное число предметов, но закон как общее суждение распространяется на необозримое конечное или бесконечное число предметов.

На основании этой проблемной ситуации возникает проблема индукции:

как возможен переход от знания о конечном ограниченном множестве предметов к знанию обо всех предметах данного множества, включая и те, которые мы не наблюдали?

Проблема индукции решается по-разному для различных видов индуктивных умозаключений. Поэтому мы сначала рассмотрим эти виды, и для каждого из них наметим решение проблемы индукции.

§ 2. Виды индуктивных умозаключений

Индуктивные умозаключения делятся на полную и неполную индукцию.

П о л н а я и н д у к ц и я

Полная индукция относится к конечным и обозримым множествам, что обеспечивает возможность исследования каждого элемента этого множества и установления присущности или неприсущности ему интересующего нас свойства или отношения.

П о л н а я и н д у к ц и я — это индуктивное умозаключение, в котором устанавливается присущность некоторого признака каждому предмету некоторого множества и на этом основании делается заключение о присущности этого признака всем предметам данного множества.

Поскольку полная индукция предполагает исследование каждого элемента исследуемого множества, заключение полной индукции дает нам достоверное знание о предметах данного множества. В этом отношении полная индукция сходна, скорее, с дедуктивными умозаключениями.

Схема полной индукции

Рассмотрим множество А = {а1, а2, ..., аn}.

Тогда полная индукция будет иметь следующий вид:

а1 имеет признак Р. а2 имеет признак Р. а3 имеет признак Р.

237

...

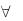
аn имеет признак Р.

Следовательно, все предметы х, принадлежащие множеству А, имеют признак Р.

На нашем языке логики предикатов эту схему можно записать следующим образом:

Р(а1) Р(а2) Р(а3)

.

.

Р (аn)

_____________

х Р(х)

где областью определения х является множество А.

П р и м е р . В 1‖в‖ классе Первой Калининградской гимназии 18 учеников.

Назовем их ―Первый ученик, Второй ученик и т.п. до Восемнадцатого ученика‖.

Установлено, что

Первый ученик любит логику. Второй ученик любит логику.

Восемнадцатый ученик любит логику.

Следовательно, все ученики 1‖в‖ класса Первой Калининградской гимназии любят логику.

П р и м е р . Частным случаем полной индукции можно считать единогласное голосование на собраниях. Здесь из того, что каждый избиратель поддерживает некоторого кандидата в городской совет, следует, что все ибиратели поддерживают этого кандидата.

Полная индукция, касающаяся таких конечных обозримых множеств, довольно тривиальна. Нетривиальность полной индукции придает рассмотрение не отдельных предметов, а всех видов предметов некоторого рода.

П р и м е р .

Конические сечения — это окружность, эллипс, парабола и гипербола. Окружность не может пересекаться прямой линией более, чем в двух точках. Эллипс не может пересекаться прямой линией более, чем в двух точках. Парабола не может пересекаться прямой линией более, чем в двух точках. Гипербола не может пересекаться прямой линией более, чем в двух точках.

Следовательно, ни одно коническое сечение не может пересекаться прямой линией более, чем в двух точках.

238

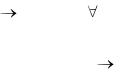
Из рассмотрения отдельных видов конических сечений мы смогли сделать вывод о конических сечениях в общем.

М а т е м а т и ч е с к а я и н д у к ц и я

Специальным видом индукции является математическая индукция, которую математики также иногда называют полной. Она отличается от ранее рассмотренной полной индукции тем, что имеет дело с бесконечным множеством предметов, но похожа на нее тем, что также дает достоверный результат. Именно поэтому она применяется в математике для доказательства теорем в математических теориях.

Математическая индукция основывается на строении и свойствах натурального ряда чисел. Хотя натуральный ряд чисел является бесконечным, он построен на очень простом законе: каждое следующее число больше предыдущего ровно на единицу. Это свойство натурального ряда позволяет доказывать общие утверждения, основываясь на следующей процедуре. Сначала мы доказываем, что нужное нам свойство присуще первому члену натурального ряда числу 1, а затем показываем, что из предположения о том, что это свойство присуще некоторому произвольному числу, назовем его n, следует, что оно присуще и следующему за ним числу, т.е. n+1. Таким образом, мы получаем способ доказательства присущности интересующего нас свойства для любого натурального числа.

Схематически математическую индукцию можно представить следующим образом.

Пусть Р – интересующее нас свойство натуральных чисел. Тогда

Математическая индукция является по характеру своего заключения дедуктивным умозаключением. Однако по своему строению она похожа на индуктивные умозаключения, поскольку в ней совершается переход от единичных суждений к общему.

Н е п о л н а я и н д у к ц и я

Если мы имеем дело с необозримыми конечными или бесконечными множествами предметов (не так хорошо упорядоченных, как натуральный ряд чисел), то нам приходится прибегать к способу умозаключений, который называется неполной индукцией.

основании знания только некоторых объектов, принадлежащих к данному множеству.

П р и м е р . Разобранный в начале этого параграфа пример с белыми лебедями представляет собой случай неполной индукции.

239

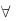
Характерной чертой неполной индукции, отличающей ее от уже рассмотренных полной и математической индукции, является то, что суждение, служащее заключением неполной индукции, в лучшем случае является истинным тойько с большей или меньшей степенью вероятности. Заключение неполной индукции не следует логически из посылок, а только подтверждается ими в большей или меньшей степени. Большая или меньшая вероятность заключения отражает эту степень подтверждения.

П р и м е р . Рассмотрим полную индукцию, в которой мы выясняли, все ли ученики 1в класса Первой Калининградской гимназии любят логику. Если бы у нас в классе присутствовали не все ученики, а допустим только шестнадцать из восемнадцати, и оказалось, что все присутствующие любят логику, то мы могли бы с большой степенью уверенности утверждать, что все ученики 1в класса любят логику. Однако научная добросовестность заставила бы нас учесть и то, что вполне может оказаться, что оставшиеся два ученика не любят логику. Таким образом, мы сказали бы, что суждение "Все ученики 1в класса любят логику" обладает высокой вероятностью, но не является достоверно истинным. В данном простом случае можно даже подсчитать эту вероятность или степень подтверждения. Действительно, 16 из 18 учеников подтвердили, что они любят логику, а относительно остальных это неизвестно. Поэтому мы можем сказать, что заключение нашей индукции имеет вероятность 16/18 или 0,89.

Приведенный пример весьма прост и ситуация, в которой мы можем так точно подсчитать вероятность истинности заключения индукции, встречается не так часто. Поэтому в так называемой индуктивной логике разрабатываются специальные методы оценки вероятности заключений индукции.

Неполная индукция бывает двух видов: популярная индукция, или индскция через простое перечисление, и научная индукция.

П о п у л я р н а я и н д у к ц и я

Полное название этого вида неполной индукции – индукция через простое перечисление при отсутствии контрпримера. Популярная индукция похожа на полную индукцию с тем только отличием, что она имеет дело с конечными необозримыми и с бесконечными множествами интересующих нас предметов.

Введем терминологию для описания популярной индукции.

Таким образом, мы получаем следующую схему популярной индукции:

а1 имеет признак Р.

240

а2 имеет признак Р.

...

аn имеет признак Р.

а1, а2, ..., аn принадлежат множеству А.

Все а, принадлежащие множеству А, имеют признак Р.

Символически эта схема1 выглядит следующим образом:

Р(а1) Р(а2)

...

Р(аn)

а1 А, а2 А, ..., аn А

_________________________

х Р(х)

Обобщение в популярной индукции основывается на том, что во всех наблюдаемых примерах элементы множества А обладают свойством Р, которое регулярно повторяется при наблюдении элементов этого множества.

Необходимым условием является то, что при этом среди наблюдаемых элементов множества А не встречается ни одного контрпримера.

Эта регулярность повторения признака и отсутствие контрпримера служат основанием для перенесения этого признака на все изучаемое множество А. Видовым признаком популярной индукции является отсутствие определенного метода отбора наблюдаемых cлучаев.

П о п у л я р н а я и н д у к ц и я – это неполная индукция, в которой отсутствует определенный метод отбора примеров, служащих посылками данного умозаключения.

П р и м е р . Классическим образцом популярной индукции является история с индуктивным обобщением "Все лебеди белы". Получилось так, что в Европе аплоть до ХVП века встречались только белые лебеди. На основе этих наблюдений было сформулировано обобщение: "Все лебеди белы". Нетрудно заметить, что при этом признак "быть белым" был перенесен с ограниченного множества лебедей, наблюдавшихся в Европе, на все необозримое тогда множество лебедей. Однако, когда в 1606 г. была открыта Австралия (тогда Новая Голландия), там были обнаружены черные лебеди. Таким образом, обобщение "Все лебеди белы" оказалось ложным.

Этот классический образец индукции показывает, что заключение популярной индукции не является достоверно истинным, но только предположительным, вероятным, или правдоподобным. Это означает, что мы не можем сказать, что заключение индукции точно истинно, а можем только сказать, что заключение истинно с некоторой большей или меньшей степенью вероятности.

1 Мы заменяем здесь а из содержательной схемы на х в соответствии с правилами нашего ЯЛП.

241

Характер популярной индукции, в которой преимущественно обращается внимание на сходство исследуемых предметов по определенному признаку, обусловливает как ее распространенность, так и ее ненадежность.

Распространенность такого рода умозаключений связана с естественной человеческой склонностью искать примеры, подтверждающие суждения, к принятию которых за истинные мы предрасположены. Популярная индукция является основанием нашей веры в предсказания астрологов и чудеса экстрасенсов. Люди, которые хотят верить в "чудеса", среди многочисленных случаев "лечения" обращают внимание только на то, что подтверждает их веру, т.е. принимают во внимание примеры и игнорируют контрпримеры. Астрологи стремятся сделать как можно больше "предсказаний" для того, чтобы что-нибудь из предсказанного сбылось, безошибочно рассчитывая на то, что публика примет во внимание именно эти, подтверждающие их предсказания, примеры, и не обратит внимание на несбывшиеся предсказания. На эту особенность мышления астрологов обращал внимание еще Августин Блаженный в своей "Исповеди" (книга VII): "... науки предсказывать будущее не существует, человеческие же догадки часто приобретают силу оракула: предсказатели не знают того, что произойдет, но, боворя о многом, натыкаются на то, что действительно произошло".

Нашу склонность к поиску единообразия в жизни и природе можно продемонстрировать и на других примерах. Так, мы склонны подмечать за одними людьми только плохое, а за другими – только хорошее, обычно игнорируя противоречащие нашей склонности примеры, и на этой основе формулируем свои обобщения о нравственных характерах людей. В основе таких оценок также лежит популярная индукция.

Приведенные примеры поясняют, почему популярная индукция не являерся надежным способом умозаключения.

Во-первых, случайный характер выбора предметов, принадлежащих интересующему нас множеству А обусловливает возможность того, что исследованное подмножество, состоящее из предметов а1, а2, ... , аn случайным образом обладает признаком Р, тогда как существуют другие подмножества А, которые этим признаком не обладают. Мы уже видели такую ситуацию на примере с лебедями и их признаком

"быть белым".

П р и м е р .

ВАргентине говорят на испанском языке.

ВЭквадоре говорят на испанскмм языке.

ВВенесуэле говорят на испанском языке.

Аргентина, Эквадор, Венесуэла — южноамериканские страны.

Следовательно, во всех южноамериканских странах говорят на испанском языке.

Хотя формально такая индукция похожа на правильную, но заключение ее ложно, потому что дальнейшее исследование показывает, что в Бразилии говорят на

португальском языке.

242

Основанием вывода в популярной индукции является простое перечисление примеров индуктивного обобщения, служащего заключением индукции, и отсутствие хотя бы одного контрпримера. Главной чертой популярной индукции, обусловливающей ее ненадежность, является то, что она не гарантирует отсутствия контрпримера.

Во-вторых, популярная индукция не учитывает разнообразия объектов изучаемого множества. Как правило, любое множество состоит из объектов различных видов, которые могут иметь различное отношение к рассматриваемому признаку. Простое перечисление случайно отобранных объектов может не учитывать какого-либо вида объектов, которому не присущ признак, приписываемый предметам данного множества

виндуктивном обобщении.

Пр и м е р . Допустим, мы хотим выяснить, знают ли студенты Калининградского государственного университета, кто такой Владимир Соловьев. Мы подходим к корпусу этого университета, задаем студентам этот вопрос и получаем на него утвердительные ответы и ни одного отрицательного. На этой основе мы можем сформулировать индуктивное обобщение: Все студенты КГУ знают, кто такой Владимир Соловьев. Однако впоследствии может выясниться, что мы спрашивали студентов возле гсманитарного корпуса университета, а опрос у корпуса естественных факультетов вполне мог дать другой результат.

Главный недостаток популярной индукции заключается в том, что процедура формирования индуктивного обобщения не дает никаких гарантий отсутствия контрпримера, а обращает в основном внимание на примеры данного индуктивного обобщения.

С этим связана логическая ошибка, свойственная популярной индукции и называемая поспешное обобщение.

П о с п е ш н о е о б о б щ е н и е – логическая ошибка, состоящая в том, что индсктивное обобщение формируется на основании немногих, случайно встретившихся примеров.

П р и м е р . 1 — простое число, 2 — простое число, 3 — простое число. 1, 2, 3 — натуральные числа. Следовательно, все натуральные числа — простые.

Здесь изучение трех первых случаев считается достаточным основанием для формирования индуктивного обобщения, относящегося ко всему бесконечному множеству натуральных чисел.

П р и м е р . Когда заболел сапожник, ему предложили лекарство, и оно помогло. Когда заболел портной, ему предложили то же самое лекарство, но портной умер. Следовательно, это лекарство полезно сапожникам и вредно портным.

Здесь индуктивное обобщение формируется на основе одного примера и случайного различия в профессиях.

Рассмотренные недостатки популярной индукции и ошибка поспешного обобщения показывает пути повышения надежности выводов по индукции:

243