6.4 Уравнения Максвелла

Основные уравнения электродинамики были установлены Максвеллом в начале 60-х годов ХIХ века. Далеко не все законы и уравнения, входящие в систему уравнений Максвелла, получены самим Максвеллом, его заслуга состоит в том, что он собрал основные уравнения электродинамики в стройную систему и сих помощью решил целый ряд вопросов. Максвелл обобщил и дополнил теорему о магнитной циркуляции (6.33). К необходимости такого обобщения можно прийти при рассмотрении такого примера. Пусть в неограниченную проводящую среду помещен заряженный шар. От этого шара врадиальных направлениях возникнут электрические токи, которые должны возбуждать магнитное поле В. Магнитное поле не может иметь радиальной составляющей, а составляющие, перпендикулярные радиусу, тоже должна быть нулю т.к. среда изотропна. Таким образом В должно равняться нулю, значит токи проводимости, - не единственная причина возникновения магнитного поля. Эту причину Максвелл назвал током смещения I_см , а сумму I + I_см - полным током. Значение тока смещения определяется условием I + I_см = 0, I = - dQ/dt, а потому по теореме Гаусса

I_см = ∫(∂D/∂t dS)

Запишем теперь полную систему уравнений Максвелла

∮(Н dl) = I + ∫(∂D/∂t dS) (6.45)

∮(Е dl) = ─ ∫(∂В/∂t dS) (6.46

∮(D dS) (6.47)

∮(ВdS) = 0 (6.48)

D = εε₀ Е (6.49)

В = μμ₀ Н (6.50)

j = λ Е (6.51)

Из уравнений Максвелла следует существование электромагнитных волн.

При распространении одномерного возмущения вдоль оси Х со скоростью v смещение описывается формулой

S = f(х ─ vt) (6.52)

Непосредственным дифференцированием можно убедится в том, смещение удовлетворяет дифференциальному уравнению

∂²s/∂х² ─ 1/v² ∂²s/∂t² = 0 , (6.53)

которое называют волновым уравнением. Как было показано Максвеллом, изменения векторов Е и Н в плоской электромагнитной волне описываются таким же волновым уравнением, скорость электромагнитной волны определяется формулой

v² 1/(εε₀μμ₀) (6.54)

Вычисления по этой формуле в случае вакуума даю значение скорости, совпадающее со скоростью света в вакууме с = 3,0 10⁸ м/с. Простейшей системой, излучающей электромагнитные волны, является диполь Герца, представляющий собой точечный диполь, дипольный момент которого быстро изменяется во времени. Как показали расчёты, произведенные Герцем, мощность излучения диполя пропорциональна четвёртой степени частоты ω. Мощность излучения движущегося одиночного заряда пропорциональна квадрату его ускорения, т.е. равномерно движущийся заряд электромагнитных волн не излучает.

Уравнения Максвелла необходимо дополнить соотношениями, определяющими энергию электромагнитной волны, плотность потока энергии определяется вектором Пойнтинга

S = [ЕН] (6.55)

Дальнейшие исследования показали, что целый ряд явлений является электромагнитными волнами, которые отличаются друг отдруга частотой. В шкалу электромагнитных волн входят (в порядке возрастания частоты ) радиоволны, инфракрасное излучение, видимое излучение, ультрафиолетовое излучение, рентгеновское излучение, γ-излучение. Важное место в современной жизни занимают радиоволны. При излучении и приёме радиоволн широко используются колебательные контуры, - системы состоящие из последовательно соединённых конденсатора С, катушки индуктивности L и резистора R, к которым подсоединён источник с переменной электродвижущей силой E. Процессы, происходящие в контуре, описываются уравнением

L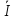 + RI + q/С = E .

Так как I = 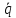, то уравнение запишется в видеγ

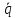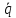L + R + q/С = 0 . (6.56)

При свободных (E = 0) колебаниях в идеальном контуре (R = 0) собственная частота контура равна

ω₀ = 1/√L͞С (6.57)

Введём обозначения R//(2L) = γ, 1/(LС) = ω₀², E/С = Х., тогда уравнение (6.56) примет вид

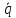+ 2γ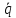 + ω₀²q = 0 (6/58)

Для его решения введём новую переменную у, полагая q = у exp( ─ γt)

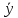(ω₀² ─ γ²) у = 0 .

Введём обозначение ω² = ω₀² ─ γ² , тогда (6.59)

q = q₀ exp(─γt) cos(ωt + δ) (6.60)

Это уравнение описывает затухающие колебания в контуре, собственная частота определяется формулой (6.59)

Рассмотрим вынужденные колебания в контуре под действием синусоидальной силы E/С =Х = Х₀ cos (ωt).

Уравнение колебаний имеет вид

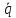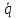+ 2γ + ω₀²q = X (6.61)

Сразу отметим, что вынужденные колебания происходят с частотой вынуждающей силы, поэтому решение будем искать в виде

q = А(ω) cos (ωt ─δ) (6.62)

Можно показать, что

А(ω) = Х₀/(( ω₀² – ω²)² + 4ω²γ²)^1/2 (6.63)

tg E = 2ωγ/ (ω₀² – ω²)^1/2 (6.64)

Как видно из (6.63) , при ω = ω₀ амплитуда вынужденных колебаний максимальна. Явление резкого возрастания амплитуды вынужденных колебаний называется резонансом. Резонанс наступает, когда частота вынуждающей силы близка к частоте собственных колебаний системы.