маткад учебник

ние этих функций требует задания дополнительного аргумента J(x, y). Это матрица размером n (n + 1). Первый столбец содержит производные ∂D/∂x. Остальные строки и столбцы представляют собой матрицу Якоби ∂D/∂yk системы ОДУ. Например, если

Программа Mathcad имеет еще несколько встроенных функций для нахождения решения только в конечной точке. Использование подобных функций позволяет экономить память ЭВМ. Имеются функции для решения систем уравнений, для части переменных которых известны начальные условия, а для других переменных – конечные условия. Подобные задачи называются двухточечными краевыми задачами. Имеются функции для решения отдельных задач в частных производных.

Подробности по использованию этих функций можно посмотреть в литературе [2, 3].

71

6. СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ

До сих пор описывалось, как Mathcad вычисляет выражения численно. При этом он возвращает после знака равенства одно или несколько чисел. Когда же Mathcad использует символьную математику, результатом вычисления выражения является другое выражение, как показано в нижней части рис. 31. При этом желаемая форма этого второго выражения может быть задана. Первоначальное выражение можно разложить на множители, проинтегрировать его, разложить в ряд и так далее. Основной целью изучения символьных вычислений является управление формой представления результата.

Численные расчеты возвращают просто число:

Символьные вычисления позволяют существенно упростить сложное выражение:

Рис. 31. Численное и символьное вычисление одно и того же выражения

Простейшие символьные упрощения делаются следующим образом: удостоверьтесь, что команда Автоматическое Вычисление в меню

Математика помечена, в противном случае сделайте это из меню;

72

введите выражение, которое нужно упростить;

нажмите [Ctrl+Period] (клавишу Ctrl, сопровождаемую точкой). Mathcad отобразит стрелку "→ " – символьный знак равенства;

щелкните мышью вне выражения. Mathcad отобразит упрощенную версию первоначального выражения. Если выражение не может быть упрощено, Mathcad просто повторит его справа от стрелки.

Символьный знак равенства является оператором, подобным любому оператору Mathcad. Когда делаются изменения где-либо выше или левее от него, Mathcad модифицирует результат.

На рис. 32 приведены примеры использования символьного знака равенства.

Если выражение упростить не удается, символьный знак равенства возвращает его неизмененным:

x2 → x2

Это аналогично поведению знака равенства в численных расчетах:

Символьный знак равенства работает также с массивами:

Рис. 32. Использование символьного знака равенства

Значительно бoльшие возможности управления результатами символьных преобразований обеспечивает меню Символы.

В Mathcad дополнительные удобства обеспечивает специальное меню, открываемое кнопкой палитры символов. В том и в другом случае появляется возможность добавлять ключевые слова (команды). При ис73

пользовании меню Символы необходимо заключить все, что требуется преобразовать в выделяющую рамку и выбрать соответствующую команду из меню Символы. Имеется важное различие между символьным преобразованием, использующим меню Символы, и преобразованием, использующим символьный знак равенства или меню палитры символов. Результаты с правой стороны от символьного знака равенства вычисляются заново всякий раз при внесении изменений в рабочий документ. Результат, полученный с использованием меню Символы, автоматически модифицироваться не будет.

В меню Символы имеется команда Стиль Вычислений, позволяющая выводить результат под исходным выражением или справа от него, а также показывать или скрывать комментарии. Рекомендуется воспользоваться этой командой при первом обращении к меню Символы.

На рис. 33 приведены примеры преобразования командами Расчеты Символические и С плавающей запятой из меню Символы.

Вычислить в символах:

ei n υ

exp(i nυ )

cos (nυ ) + i sin(nυ )

π

3.14159265358979323846264338328

– результат расчета с плавающей запятой (30 значащих цифр)

.886226925452758013649083741670

Рис. 33. Символьные преобразования, доступные из пункта меню

При преобразовании выражений, содержащих комплексные числа, командой Комплексные Mathcad выразит результаты в виде a + bi.

В отличие от обычных вычислений Mathcad, которые проводятся с пятнадцатью десятичными числами, при использовании команды С пла-

74

вающей запятой можно управлять количеством значащих цифр. После ввода команды С плавающей запятой Mathcad предложит выбрать количество значащих цифр от 1 до 4000.

6.1. Расчеты

Для разложения функций в ряды следует выделить переменную, по которой требуется найти разложение и выбрать команду Разложить на составляющие… из меню Переменные. Диалоговое окно запросит порядок остаточного члена. На рис. 34 приведены примеры разложения функций sin x и ln(x + 1).

Для разложения выражения (х + у)4 его следует выделить рамкой и использовать команду Расширить. Аналогично раскладывается выражение cos5x.

Для разложения выражения на множители используется команда Фактор. Для разложения на элементарные дроби необходимо выделить переменную в знаменателе и выбрать команду Преобразование в частичные доли. Напомним, что для обратного преобразования от суммы элементарных дробей в произведение нужно выделить все выражение.

Для выражения производных, определенных и неопределенных интервалов, сумм, произведений и пределов удобно использовать кнопку палитры символов с изображением интеграла. Примеры этих вычислений приведены на рис. 35.

При использовании операторов необходимо помнить, что следует заполнять все зарезервированные места ввода. Если результат может быть вычислен точно, то появится точный ответ. В противном случае Mathcad будет возвращать в качестве ответа первоначальное выражение.

При вычислении неопределенного интеграла следует помнить, что результат интегрирования неоднозначен. Если f(x) – интеграл данной функции, то для любой константы С интегралом будет также f (x) + С. Таким образом, ответ, получаемый Mathcad, может отличаться на константу от ответа, который можно найти в таблицах. Если продифференцировать функцию, например sin t + 5 (см. рис. 35), и затем проинтегрировать результат, необязательно в качестве ответа получится исходная функция. В тех случаях, когда символьный процессор не сможет найти неопределенный интеграл, появится сообщение об ошибке.

При символьном вычислении определенного интеграла символьный процессор пытается найти неопределенный интеграл от подынтеграль-

75

(x + y)4 Выделите выражение и выберите Расширить x4 + 4x3 y + 6x2y2 + 4x y3 + y4

cos (5x)

16cos (x)5 − 20cos (x)3 + 5cos (x)

Рис. 34. Разложение функций

76

Рис. 35. Примеры символьных преобразований

77

ного выражения перед подстановкой пределов интегрирования. Если символьное интегрирование проведено успешно и пределы интегрирования – целые числа, обыкновенные дроби, точные константы, подобно π , или пределы бесконечные, процессор выдаст точное значение интеграла. Если подынтегральное выражение или один из пределов содержит десятичную точку, символьный ответ будет числом, отрабатываемым с двадцатью значащими цифрами (по умолчанию). Изменить число значащих цифр можно с помощью пункта меню Расчеты С плавающей запятой. В отличие от символьного интегрирования программа численного интегрирования находит значения подынтегрального выражения во многих точках на отрезке интегрирования и использует эти значения, чтобы аппроксимировать интеграл.

Различия в выполнении одних и тех же операций в символьных и численных режимах объясняется тем, что символьная математика - не развитие пакета Mathcad, а приобретение фирмой MathSoft программного модуля у фирмы Maple.

Если необходимо проводить сложные символьные преобразования, выходящие за рамки возможностей Mathcad, то следует воспользоваться пакетом Maple или Derive.

Вообще говоря, символьный и численный процессоры Mathcad не связаны друг с другом. Из-за этого можно заниматься сложными численными вычислениями, не зная, что можно свести их к эквивалентной, но намного более простой проблеме разумным использованием символьного процессора.

Например, если требуется вычислить выражение типа

u v w

∫∫∫ (x2 + y2 + z2 )dxdydz,

0 0 0

Mathcad предпринял бы трудоемкую задачу вычисления численной аппроксимации тройного интеграла. Символьный процессор исследовал бы тройной интеграл и возвратил бы эквивалентное, но более простое выражение

1 (w3vu + wv3u + wvu3). 3

Для решения подобных задач в Mathcad есть возможность, выбирая пункт Оптимизация из меню Математика, заставить эти два процес-

78

сора общаться друг с другом. Если команда Оптимизация подключена (помечена слева в меню Математика) и Mathcad находит более простую форму для выражения, он реагирует следующим образом:

отмечает область красной звездочкой; заменяет внутреннее представление выражения его упрощенной фор-

мой. Отображаемое выражение остается неизменным; вычисляет эквивалентное выражение вместо заданного. Чтобы уви-

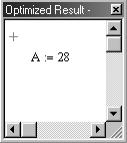
деть это выражение, дважды щелкните мышью на красной звездочке позади области (см. рис. 36).

Выберите пункт Оптимизация из меню Математика

Звездочка показывает, что символьный процессор нашел упрощенную форму данного выражения.

Упрощение выражения экономит время – теперь не нужно вычислять интеграл вообще.

Рис. 36. Вычисление интеграла по упрощенной формуле

6.2. Преобразования Фурье и Лапласа

Прямое и обратное преобразования Фурье функции f(t) определяются формулами

∞

F (ω )= ∫ f (t)e−iω tdt,

−∞

79

Рис. 37. Преобразования Фурье и Лапласа

Чтобы получить преобразование Фурье, необходимо: ввести выражение, которое нужно преобразовать; щелкнуть мышью на переменной преобразования;

выбрать последовательно Символы, Преобразование и Фурье.

80