
маткад учебник
.pdfmod(x, y) – остаток от деления x на y. Результат имеет тот же самый знак, что и x;
angle(x, y) – угол (в радианах) между положительной полуосью x и вектором (x, y) в плоскости XY. Аргументы должны быть вещественны. Возвращает значение между 0 и 2π .
ceil(3.25) = 4 |
|
floor(3.25) = 3 |
|
|
||
mantissa (x) := x − floor(x) |
mantissa (3.45) = 0.45 |
|||||
Традиционное округление: |
|
|
|
|||
roundoff (x) |
:= |
if(mantissa (x) |
< , |
, |
ceil(x)) |
|
|
0.5 floor(x) |
|
||||
roundoff (3.46) = 3 |
roundoff (3.56) = 4 |
|
||||
Рис. 14. Создание функций округления
На рис. 14 показано, как из этих функций могут быть сформированы функции округления.
4.4.Дискретное преобразование Фурье
ВMathcad входят два типа функций для дискретного прямого и обратного преобразования Фурье: fft/ifft и cfft/icfft. Эти функции дискретны: они берут в качестве аргументов и возвращают векторы и матрицы. Они не могут быть использованы с другими функциями.
Используйте функции fft и ifft, если выполнены два следующих условия: аргументы вещественны, и вектор данных имеет 2m элементов.
Первое условие необходимо, потому что функции fft/ifft используют тот факт, что для вещественных данных вторая половина преобразования Фурье является комплексно сопряженной с первой. Mathcad отбрасывает вторую половину вектора-результата. Это сохраняет время и память при вычислениях.
Пара функций cfft/icfft не использует симметрию в преобразовании. По этой причине необходимо использовать их для комплексных данных.
41
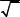
Второе условие требуется, потому что пара функций fft/ifft использует высоко эффективный алгоритм быстрого преобразования Фурье. Для этого вектор аргумента, используемого с fft, должен иметь 2m элементов. В функциях cfft/icfft использован алгоритм, который допускает в качестве аргументов как матрицы, так и векторы произвольного размера. Когда эта пара функций используется с матрицей в качестве аргумента, вычисляется двумерное преобразование Фурье.
Следует иметь в виду, что если для прямого преобразования использована функция fft, то для обратного преобразования необходимо использовать функцию ifft. Аналогично используются функции cfft/icfft.
4.5. Преобразование Фурье в вещественной области
Для вещественных векторов с 2m элементами предпочтительно использовать функции fft/ifft. Функция fft(v) возвращает дискретное преобразование Фурье, векторный аргумент которой можно интерпретировать как результат измерений через равные промежутки времени некоторого сигнала. Вектор v должен содержать 2m элементов. Результат – комплекснозначный вектор размерности 1 + 2m–1. Если v имеет размерность, отличную от 2m, Mathcad выдает сообщение об ошибке "неверный размер вектора".
Элементы вектора, возвращаемого fft, вычисляются по формуле
n−1
Cj n k∑=0 vk e2π i( j n)k .
n)k .
Вэтой формуле n – число элементов в v, i – мнимая единица. Элементы в векторе, возвращенном функцией fft, соответствуют различным частотам. Чтобы восстановить фактическую частоту, необходимо знать частоту измерения исходного сигнала. Если v есть n-мерный вектор, переданный функции fft, и частота измерения исходного сигнала – fs, то частота, соответствующая Ck
fk = k fs. n
Обратите внимание, что это делает невозможным обнаружить частоты выше частоты измерения исходного сигнала. Это ограничение, налагаемое не Mathcad, а самой сутью проблемы. Чтобы правильно восстановить сигнал по его преобразованию Фурье, необходимо произвести
42
i := 0.. 63 |
|
|
|
|
|
|
|
|
|
Формирование сигнала: |
|
|
π |
i |
|
|
|||
|
xi := sin |
|
+ rnd(1) − 0.5 |
|
|||||
|
|
|
|
|
|
|
10 |
|
|
Применяется комплексное преобразование Фурье: |
|
||||||||
c := fft(x) |
|
|
N := last(c) |
|
N = 32 |
|
|
|
|
Обращение преобразования Фурье: |
z := ifft(c) |
|
|||||||
N2 := last(z) |
|
N2 = 63 |
|
j := 0.. N |
|
k := 0.. N2 |
|
||
Графическое представление сигнала |
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
zk = |
xj = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–0.499 |
–0.499 |
|
|
|
|
|
|
|
|
2.34·10 –3 |
2.34·10–3 |
xi |
0 |
|
|
|
|
|
|
0.673 |
0.673 |
|
|
|
|
|
|
0.659 |
0.659 |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1.274 |
1.274 |
|
–2 |
|
|
|
|
|
|
0.674 |
0.674 |
|
0 |
20 |
40 |
60 |
80 |
|
1.162 |
1.162 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
i |
|
|
|
0.613 |
0.613 |
Фурье-образ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0.179 |
0.179 |
|
4 |
|
|
|
|
|
|
–0.044 |
–0.044 |
|
|
|
|
|
|
|
|
0.489 |
0.489 |
|
|
|
|
|
|
|
|
–0.69 |
–0.69 |
cj |
2 |
|
|
|
|
|
|
–1.079 |
–1.079 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
–0.777 |
–0.777 |
|
|
|
|
|
|
|
|
–0.849 |
–0.849 |
|
0 |
|
|
|
|
|
|
–1.334 |
–1.334 |
|
0 |
10 |
20 |
30 |
40 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
j |
|
|
|
|
|
|
Рис. 15. Быстрые пр6еобразования Фурье в Mathcad |
||||||||
43

измерения исходного сигнала с частотой, по крайней мере, вдвое большей, чем ширина полосы частот. Подробное обсуждение этой проблемы содержится в специальных курсах.
Функция ifft(v) возвращает обратное дискретное преобразование Фурье. Вектор v должен иметь 1 + 2m элементов, где m – целое. Результат есть вектор размерности 2m+1.
Аргумент v – вектор, подобный созданному функцией fft. Чтобы вычислить результат, Mathcad сначала создает новый вектор w, комплексно сопряженный v, и присоединяет его к вектору v. Затем Mathcad вычисляет вектор d, элементы которого вычисляются по формуле
|
|
1 |
n−1 |
|
||
d j |
= |
∑ |
wk e |
−2π i( j n)k . |
||
|
||||||
|
|
n k =0 |
|
|||
Это та же самая формула, что и для fft, кроме знака минус в функции экспоненты. Функции fft и ifft – точные обращения. Для всех вещественных v справедливо ifft(fft(v)) = v.
Пример использования прямого и обратного преобразований Фурье приведен на рис. 15.
4.6. Альтернативные формы преобразования Фурье
Определения преобразования Фурье, рассмотренные выше, не являются единственно возможными. Например, часто используются следующие определения прямого и обратного преобразований Фурье:
F (ν) = 1 |
∑n |
f (τ)e−2π i(ν n)τ ; f ( τ) ∑=n |
F ( ν)e2π i(τ / n)ν. |
n |
τ=1 |
v =1 |
|
Эти определения реализованы во встроенных функциях FFT/IFFT и ICFFT. Они отличаются от быстрого преобразования Фурье следующим:
вместо коэффициента 1 n перед обеими формулами стоит коэф-
n перед обеими формулами стоит коэф-
фициент 1/n и коэффициент 1 в обратном преобразовании;
знак минус появляется в показателе экспоненты прямого преобразования и исчезает в формуле обратного.
4.7. Кусочно-непрерывные функции
Кусочно-непрерывные функции полезны для управления ветвлениями и остановками вычислительных процессов. Имеются пять функций
44
Использование условных операторов |
x := −2, −1.8.. 2 |
f( x) := x2 − 1 |
|||||||
|
|
|
|
|
|||||
g( x) := if( f(x) > 0, f( x) , 0) |
|
g(x) равна f(x), когда f(x) > 0, иначе 0 |
|||||||
|
4 |
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
g(x) |
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
0 |
|
2 |
|
0 |
|
0 |
2 |
|
2 |
|
|
2 |
|
||||
|
|
x |
|
|
|
|
|
x |
|
h( x) := if( x ≥ 1, f(x) , −f( x) ) |
|
|
|
|
|
|
|
||
|
5 |
|
|
|
|
иначе |
–f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
h(x) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжать вычисления до |
||||
|
|
|
|
|
выполнения условия |
|
|||
|
5 |
|
|
|
|
quess 2 − a |
|
|
|
|
2 |
0 |
|
2 |
|
< err |
|
||
|
|
x |
|
|
|
|
|
|
|
N := 100 |
i := 0.. N |
a := 1000 |
quess 0 := 10 |
err := 10− 2 |
|
||||
|
|
|
|
|
quess i + |
a |
|
|
|
|
|
(quess i)2 − a |
|
|
|
|
|
||
quess i+1 |
:= until |
− err, |
|
quess i |
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
N2 := last(quess ) − 1 |
j := 0.. N2 |
j = |
quess j = |
(quess j)2 = |
|||||
Число итераций |
N2 = |
5 |
|
0 |
|
10 |
|
100 |
|
|
1 |
|
55 |
|
3.025·103 |
||||
|
|
|
|
|
|
|
|||
answer := quess N2 |
|
|
2 |
36.591 |
|
1.339·10 3 |
|||
|
|
|
|
|
|
1.021·10 3 |
|||
answer = 31.623 |
|
|
|
3 |
31.96 |
|
|||
|
|
|
4 |
31.625 |
|
1·10 3 |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
5 |
31.623 |
|
1·103 |
|
|
Рис. 16. Условные выражения в Mathcad |
|
|
||||||
45
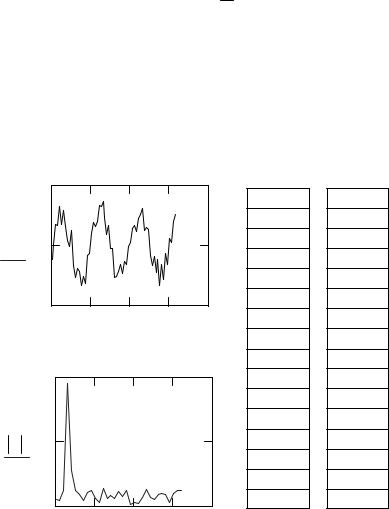
Mathcad, относящихся к этому классу. Функция if полезна для выбора одного из двух значений, определяемого условием. Ступенчатая функция Хевисайда Ф(х) и символ Кронекера δ(m, n) во многом аналогичны функции if. Функция until используется, чтобы управлять процессом итераций.
Функция if(cond, tval, fval) возвращает значение tval, если cond отличен от 0 (истина) и возвращает fval, если cond равен 0 (ложь). Обычно в качестве аргумента cond выбирается булево выражение вида w = z, x > y, x < y, x ≥ y, x ≤ y, w ≠ z. Можно объединять булевы операторы, чтобы записать более сложные условия.
Например, условие
(x < 1) (x > 0)
действует подобно логическому "и", возвращающему 1, только если x заключено между 0 и 1.
Аналогично выражение
(x > 1) + (x < 0)
действует подобно логическому "или", возвращающему 1, если x > 1, или x < 0, и 0, если x заключено между 0 и 1.
Функция until (x, z) возвращает z, пока выражение x не становится отрицательным; должно содержать дискретный аргумент. Функция until позволяет останавливать вычисления для последовательных значений дискретного аргумента. Функция until полезна в итеративных процессах с определенным условием сходимости.
На рис. 16 приведены примеры использования функций if и until. Функция Хевисайда эквивалентна следующей функции:
Ф(x):= if (x <0,0,1)
Символ Кронекера δ(m, n) возвращает 1, если m = n; иначе 0. Оба аргумента должны быть целочисленными. Символ Кронекера эквивалентен функции
δ(m, n): =if (m = n,1,0)
Ступенчатая функция Хевисайда может быть использована для создания импульса шириной w:
pulse (x, w ):= Ф(x) − Ф(x − w)
Можно определить также две полезные функции lowpass и highpass. Они обе являются фильтрами – умножение на них какого-либо сигнала
46

вырезает из этого сигнала кусок вокруг точки x, имеющий ширину 2w. Разница состоит в том, что lowpass оставляет только вырезанный кусок, highpass – все, кроме вырезанного куска.
lowpass (x, w ):= pulse (x+w, 2 w ) highpass (x, w ):= 1 − pulse (x+w, 2 w )
4.8. Статистические функции
Для вычисления статистических оценок случайных совокупностей чисел в Mathcad могут использоваться следующие функции:
mean(A) – возвращает среднее значение элементов массива А размерности m × n по формуле
m−1 n−1
mean(A) = 1 ∑ ∑ Aij ; mn i=0 j=0
var(A) – возвращает дисперсию элементов массива А размерности m × n согласно формуле
m−1 n−1
2
var(A) = 1 ∑ ∑ Aij − mean(A) ; mn i=0 j=0
stdev(A) - возвращает среднеквадратичное отклонение (квадратный корень из дисперсии) элементов m × n массива А
stdev(A) = var(A).
4.9. Плотности распределения вероятности
Эти функции показывают отношение вероятности того, что случайная величина попадает в малый диапазон значений с центром в заданной точке, к величине этого диапазона. В Mathcad имеются функции семнадцати плотностей вероятностей. Отметим только некоторые из них: dnorm(x, µ, σ ) – возвращает плотность вероятности нормального рас-
пределения
dnorm(x,µ, σ) = |
1 |
|
− |
(x − µ)2 |
|||
|
exp |
|
|
|
, |
||
2πσ |
2σ |
2 |
|
||||
|
|
|
|
|
|||
47
в котором µ и σ есть среднее значение и среднеквадратичное отклонение, σ > 0;
dunif(x, a, b) – вычисляет плотность вероятности равномерного распределения
1 |
|
x |
[ |
] |
|
|
|
, |
|||
dunif(x, a,b) = b − a |
|
a;b , |
|||
|
x [a b] |
||||
|
0, |
|
|||
|
|
|
|
|
|
вкотором a и b являются граничными точками интервала, a < b.
4.10.Функции распределения
Эти функции возвращают вероятность того, что случайная величина меньше или равна определенному значению. Функция распределения вероятности – это функция плотности вероятности, проинтегрированная от минус бесконечности до определенного значения.
Приведем две из них:
pnorm(x, µ, σ ) – возвращает функцию нормального распределения со средним µ и среднеквадратическим отклонением σ (σ > 0);
punif(x, a, b) – возвращает функцию равномерного распределения. a и b есть граничные значения интервала (a < b).
Mathcad имеет ряд функций для генерирования случайных чисел, имеющих разнообразные распределения вероятностей. Приведем две из них:
rnorm(m, µ, σ ) – возвращает вектор m случайных чисел, имеющих нормальное распределение (σ > 0);
runif(m, a, b) – возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором a и b являются граничными точками интервала (a < b).
Остальные встроенные статистические функции и их описания можно посмотреть, выбрав команду Функция из меню Вставка.
4.11. Интерполяция и функции предсказания
Интерполяция заключается в использовании значений некоторой функции, заданных в ряде точек, чтобы предсказать значения между ними. В Mathcad можно или соединять точки данных прямыми линиями (линейная интерполяция) или соединять их отрезками кубического полинома (кубическая сплайн-интерполяция).
48
В отличие от функций регрессии, обсуждаемых в следующем разделе, функции интерполяции определяют кривую, точно проходящую через заданные точки. Из-за этого результат очень чувствителен к ошибкам данных. Если данные зашумлены, следует рассмотреть возможность использования регрессии вместо интерполяции.
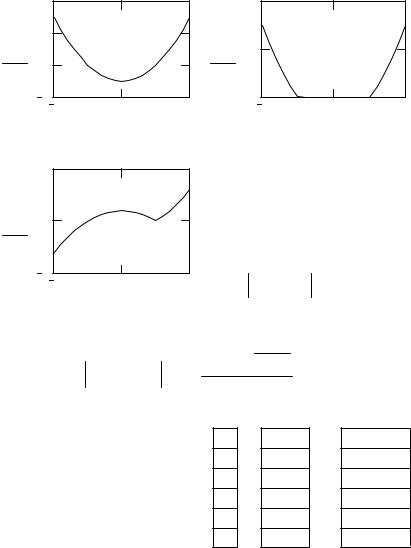
Для линейной интерполяции используется функция linterp(vx, vy, x), которая по векторным данным vx и vy возвращает линейно интерполируемое значение y, соответствующее третьему аргументу x. Аргументы vx и vy должны быть векторами одинаковой длины. Вектор vx должен содержать вещественные значения, расположенные в порядке возрастания. Эта функция соединяет точки данных отрезками прямых, создавая, таким образом, ломаную линию. Интерполируемое значение для конкретного x есть ордината y соответствующей точки ломаной.
Пример линейной интерполяции показан на рис. 17.
Кубическая сплайн-интерполяция позволяет провести кривую через набор точек таким образом, что первые и вторые производные кривой непрерывны в каждой точке. Эта кривая образуется путем создания ряда кубических полиномов, проходящих через наборы из трех смежных точек. Кубические полиномы состыковываются друг с другом, чтобы образовать одну кривую.
Чтобы провести кубический сплайн через набор точек:
создайте векторы vx и vy, содержащие координаты x и y, через которые нужно провести кубичный сплайн. Элементы vx должны быть расположены в порядке возрастания;
вычислите вектор vs:=cspline(vx, vy). Вектор vs содержит вторые производные интерполяционной кривой в рассматриваемых точках.
Чтобы найти интерполируемое значение в произвольной точке, скажем х0, вычислите interp(vs, vx, vy, x0), где vs, vx и vy – векторы, описанные ранее.
Обратите внимание, что можно сделать то же самое, вычисляя interp(cspline(vx, vy),vx,vy, x0).
Пример использования кубической сплайн-интерполяции приведен на рис. 17 внизу.
49
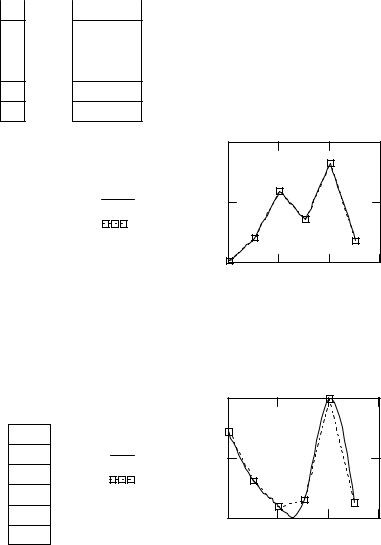
Линейная интерполяция |
|
|||
|
i := 0.. 5 |
VXi:=i |
VY :=vd(1) |
|
|
|
|
|
i |
|
VXi = |
VYi = |
linterp(VX, VY, 1.5) = 0.389 |
|
|
|
|
|
|
01.268·10–3
1 |
|
0.193 |
linterp(VX, VY, 3.75) = 0.705 |
|
|
|
|
2 |
|
0.585 |
linterp(VX, VY, 4.1) = 0.758 |
|
|
|
|
3 |
|
0.35 |
|
|
|
40.823
5 |
x :=0, 0.1.. 5 |
|
|
|
0.174 |
|
|
|
|
|
1 |
|
|
|
|
linterp(VX , VY, x) |
|
|
|
|
0.5 |
|
|
|
|
VYi |
|
|
|
|
0 |
2 |
4 |
6 |
|
0 |
|||
Кубическая сплайн-интерполяция |
|
x , VXi |
|
|
|
|
|
||
i := 0.. 5 |
VXi := i |
VYi := rnd(1) |
VS := lspline(VX, VY) |
|
interp(VS, VX, VY, 1.5) |
= 0.188 |
interp(VS, VX, VY, 3.75) = 0.868 |
||
interp(VS, VX, VY, 4.1) |
= 0.989 |
|
|
|
VYi =
0.71
interp(VS , VX , VY, x)
0.304
0.091 VYi
0.147
0.989
0.119
1 |
|
|
|
0.5 |
|
|
|
0 |
2 |
4 |
6 |
0 |
|||
|
|
x, VXi |
|
Рис. 17. Примеры интерполяции
50
