
маткад учебник
.pdf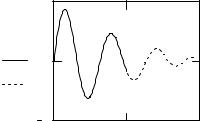
Кроме функции cspline, Mathcad имеет еще две кубические сплайнфункции: lspline и pspline.
Эти три функции отличаются только граничными условиями: функция lspline генерирует кривую сплайна, которая приближается к
прямой линии в граничных точках;
функция pspline генерирует кривую сплайна, которая приближается к параболе в граничных точках;
функция сspline генерирует кривую сплайна, которая может быть кубическим полиномом в граничных точках.
Использование функций lspline и pspline аналогично использованию функции сspline. Для определения кривой наилучшей интерполяции удобно сравнить все три функции.
Если необходимо оценить значения функции в точках, находящихся вне области заданных значений функции, то следует использовать алгоритм экстраполяции, реализованный в функции predict(v, m, n), которая возвращает n предсказанных значений, основанных на m последовательных значениях вектора данных v. Элементы v должны представлять собой значения, взятые через равные интервалы. Рекомендуется исполь-
k := 0.. 99
Существующие данные
Предсказанные значения
|
−k |
|
|
k |
||
data k := exp |
|
|
|
sin |
|
|
|
|
|
||||
|
100 |
|
|
10 |
||
p := predict(data , |
6 |
, 100) |
|
|
||
i := 0, 5.. 99
1 |
|
|
data k |
|
|
0 |
|
|
pi |
|
|
1 0 |
100 |
200 |
|
k , i+100 |
|
Рис. 18. Использование функции предсказания для экстраполяции данных
51
зовать эту функцию, когда экстраполируемая функция является гладкой и осциллирующей, но не обязательно периодической.
Пример использования функции predict приведен на рис. 18.
4.12. Функции регрессии
Функции регрессии создают кривую или поверхность, которая минимизирует ошибку между собой и имеющимися данными. В отличие от функций интерполяции, рассмотренных в предыдущем разделе, эти функции не требуют, чтобы аппроксимирующая кривая или поверхность проходили через точки данных. Функции регрессии гораздо менее чувствительны к ошибкам данных, чем функции интерполяции. Конечный результат регрессии – функция, с помощью которой можно оценить значения в промежутках между заданными точками.
В Mathcad имеются функции четырех видов регрессии: линейная, полиномиальная, многомерная полиномиальная, обобщенная.
При использовании функций линейной регрессии определяется наклон и смещение линии, которая будет приближена к исходным данным с наименьшим среднеквадратическим отклонением.
Если поместить значения x в вектор vx и соответствующие значения y в vy, то линия определяется в виде
y = slope(vx, vy) x + intercept(vx, vy). |
|||
i := 0.. 40 |
xi := 10 i |
yi := 10 i + 100 rnd(1) |
|
Вычисляются коэффициенты линейной регрессии: |
|||
a := slope (x, y) |
a = 1.079 |
|
|
b := intercept (x, y) |
b = 34.417 |
||
|
600 |
|
|
yi |
400 |
|
|
|
|
|
|
a xi + b |
200 |
|
|
|
|
|
|
|
0 |
20 |
40 |
|
0 |
||
|
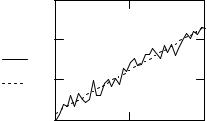
Рис. 19. Линейная регрессия |
||
52
Здесь функции slope и intercept возвращают скаляры: наклон и смещение по оси ординат линии регрессии.
Рис. 19 показывает, как можно использовать эти функции, чтобы провести линию через экспериментальные точки.
Эти функции полезны не только тогда, когда данные по существу должны представлять линейную зависимость, но и когда они представляют экспоненциальную зависимость. Например, если x и y связаны соотношением вида
y = Aekx ,
можно применить эти функции к логарифму данных и использовать факт, что
ln y = ln A + kx.
В этом случае
A = exp (intercept(vx, vy)), k = slope(vx, vy).
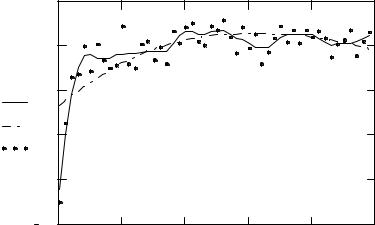
Полиномиальная регрессия используется в том случае, когда между y и x, полученными экспериментально, ожидается полиномиальная зависимость. При этом используются функции regress(vx, vy, n) или loess(vx, vy, span). Здесь n – порядок полинома, который должен приближать данные из vx и vy. Аргумент span (span > 0) определяет, насколько большие окрестности функция loess будет использовать при выполнении локального приближения. Функции regress и loess возвращают векторы (обозначим vs), которые используются функцией interp(vs, vx, vy, x), которая для заданного значения х возвращает интерполируемое значение y.
Пример использования функции loess при двух значениях аргумента span приведен на рис. 20.
Обобщенная регрессия используется в том случае, когда нужно искать приближение экспериментальной зависимости в виде комбинации произвольных функций, не являющейся полиномом. Если предполагается, что данные могли бы быть смоделированы в виде линейной комбинации произвольных функций
y = a0 f0(x) + a1 f1(x) + ... + an fn (x),
следует использовать функцию linfit, чтобы вычислить ai.
53
Создание данных: |
|
|
|
|
||
i := 0.. 49 |
vxi := i |
vzi := 0.5(rnd(1) − 0.5) + atan (i) |
|
|||
Случай 1: |
Span1 := 0.2 |
|
Случай 2: |
Span2 := 2 |
|
|
vs1 := loess (vx, vz, Span1) |
|
vs2 := loess (vx, vz, Span2) |
|
|||
f1(x) := interp(vs1 , vx, vz, x) |
|
f2(x) := interp(vs2 , vx, vz, x) |
|
|||
Отображение данных: |
|
|
|
|
||
|
2 |
|
|
|
|
|
|
1.5 |
|
|
|
|
|
f1(vxi ) |
1 |
|
|
|
|
|
f2(vxi ) |
|
|
|
|
|
|
vzi |
0.5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0.5 |
10 |
20 |
30 |
40 |
50 |
|
0 |
|||||
|
|
|
|
i |
|
|
|
|
Рис. 20. Полиномиальная регрессия |
|
|
||
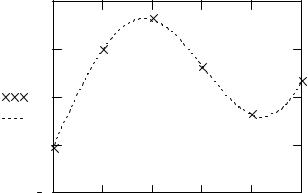
На рис. 21 показан пример, в котором линейная комбинация трех функций – x, х2 и sin5x используется для аппроксимации некоторых данных.
54
|
0 |
|
|
−0.066 |
|
|
|
|
|
0.2 |
|
|
1.969 |
|
|
|
|
|
|
|
|
t |
||||
vt := |
0.4 |
|
vy := |
2.611 |
|
|
|
|
F(t) := |
t2 |
|
||||||
|
0.6 |
|
|
1.604 |
|
|
|
|
|
0.8 |
|
|
0.623 |
|
|
sin(5t) |
|
|
|
|
|
|
|
|
||
|
1 |
|
|
1.321 |
|
|
|
|
|
|
|
0.466 |
S := linfit(vt , vy , F) |
S = |
|
|
|
2.893 |
||
|
|
|
2.124 |
g(t) := F(t)S |
j := 0.. 5 |
|
t := 0, 0.01.. 1 |
3
2
vy j
1
g( t)
0
1
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
vt j , t |
|
|
Рис. 21. Обобщенная регрессия
55
5. РЕШЕНИЕ УРАВНЕНИЙ
Mathcad позволяет решать уравнения и системы уравнений. Максимальное число уравнений и неизвестных в системе равно пятидесяти.
5.1. Численное решение уравнения с одним неизвестным
Для решения одного уравнения с одним неизвестным используется функция root(f(z), z), которая возвращает значение z, при котором выражения или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. Рассмотрим пример, как найти а – решение уравнения ex = x3. Предварительно нужно присвоить числовое значение второму аргументу функции root. Это значение становится первым приближением к искомому корню. Функция root использует для поиска корня метод секущей. Когда значение выражения f (z) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Для рассматриваемого примера запишем первое приближение
x := 3
Определим выражение, которое должно быть обращено в ноль. Для этого перепишем уравнение х3 = eх в виде х3 – ех = 0.
Определим переменную а как корень уравнения
a := root(x3 – ex, x)
Наберите [а=], чтобы увидеть на экране результат
а = 1.857
При использовании функции root имейте в виду следующее: удостоверьтесь, что переменной присвоено начальное значение до
начала использования функции root;
для выражения с несколькими корнями, например х2 – 1 = 0, начальное значение определяет корень, который будет найден Mathcad. В этом
56
Дано уравнение: |
x3 − 10x + |
2 = 0 |
x := −5, −4.95.. 5 |
||
|
100 |
|
|
|
|
x3−10 x+2 |
0 |
|
|
|
|
|
100 |
2.5 |
0 |
2.5 |
5 |
|
5 |
||||
|
|
|
x |
|
|
Для нахождения трех различных корней используем |
|||||
три начальных приближения |
|
|
|||
x := −2 |
( |
3 |
− 10 x + |
) |
= −3.258 |
|
|
|
|
|
|
root x |
2, x |
|
|
|
|
|
|
||||
x := 0 |
( |
3 |
− 10 x + |
) |
= 0.201 |
|
|
|
|
|
|
root x |
2, x |
|
|
|
|
|
|
||||
x := 3 |
( |
3 |
− 10 x + |
) |
= 3.057 |
|
|
|
|
|
|
root x |
2, x |
|
|
|
|
|
|
||||
Дано уравнение |
x2 + 1 = 0 |
, которое имеет |
|
|
|
|
|
||||
два мнимых корня |
x1 = i, x2= –i. |
|
|
|
|
|
|
|
|||
Вычислим эти корни с помощью Mathcad с разной точностью |
|
|
|
||||||||
− 3 |
|
x := 1 + 2i |
|
( 2 |
+ |
) |
= −1.471× |
− |
5 |
+ i |
|
TOL = 1 × 10 |
|
|
root x |
1, x |
10 |
|
|||||
− 6 |
|
x := 1 + 2i |
|
( 2 |
+ |
) |
= −2.81 × |
− 8 |
+ i |
||
TOL := 10 |
|
|
root x |
1, x |
10 |
||||||
− 7 |
|
x := 1 + 2i |
|
( 2 |
+ |
) |
= i |
|
|
|
|
TOL := 10 |
|
|
root x |
1, x |
|
|
|
||||
− 7 |
|
x := 1 − 2i |
|
( 2 |
+ |
) |
= −i |
|
|
|
|
TOL := 10 |
|
|
root x |
1, x |
|
|
|
||||
Рис. 22. Вычисление корней уравнений
57
случае рекомендуется построить график функции и определить подходящие начальные приближения для отыскания каждого корня. В некоторых случаях удобно несколько раз изменить масштаб графика. Если два корня расположены близко друг от друга, можно уменьшить значение TOL, чтобы различить их;
если f (x) имеет малый наклон около корня, функция root(f(x), x) может сходиться к значению r, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x) = 0 на g(x) = 0, где
g(x) = |
f (x) |
; |
|
|
|||
|
d |
f (x) |
|
|
|
||
|
dx |
||
для выражения f(x) с известным корнем а нахождение дополнительных корней f(х) эквивалентно поиску корней уравнения h(х) = 0, где h(х) = f(х)/(х – а). Часто бывает проще искать корень выражения h(х), определенного выше, чем пробовать искать другой корень уравнения f(х) = 0, выбирая разные начальные приближения.
Пример поиска нескольких корней с помощью функции root и использования графика функции приведен на рис. 22.
Функция root позволяет находить и комплексные корни. Для поиска комплексного корня следует использовать комплексное число в виде начального приближения.
Что делать, когда функция root не сходится?
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение "отсутствует сходимость". Эта ошибка может быть вызвана следующими причинами:
уравнение не имеет корней; корни уравнения расположены далеко от начального приближения;
выражение имеет локальные максимумы или минимумы между начальным приближением и корнями;
выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Обычно для установления причины ошибки достаточно подробно исследовать график f(х).
58
В инженерной практике часто приходится решать уравнения при многократном изменении параметров. Например, пусть требуется решить уравнение ех = ах2 для нескольких различных значений а. Самый простой способ состоит в определении функции
f (a, x ):= root (ex − a x2, x )
Затем присвойте конкретные значения параметру a и начальное значение переменной x как аргументам этой функции.
Задача: решить уравнение |
ex = a x2 при различных значениях a. |
Определим функцию f, решающую уравнение для заданного a:
f(a , x) := root (ex − a x2 , x)
Решение уравнения для ряда значений a:
a := 1.. 5 |
x 0:= 1 |
(начальное приближение) |
Начальное приближение для каждого значения a есть корень, соответствующий предыдущему значению:
xa := f(a, xa−1)
Ответы: |
|
Проверка: |
|
|
||||
|
a = |
xa = |
|
exa = |
a (xa)2 = |
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
–0.703 |
|
0.495 |
|
0.495 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
–0.54 |
|
0.583 |
|
0.583 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
–0.459 |
|
0.632 |
|
0.633 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
–0.408 |
|
0.665 |
|
0.665 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
–0.371 |
|
0.69 |
|
0.69 |
|
|
|
|
|
|
|
|
|
|
Рис. 23. Определение функции пользователя с функцией root
Иллюстрация решения этой задачи приведена на рис. 23.
59
5.2. Нахождение корней полинома
Для нахождения корней выражения, имеющего вид anxn + an–1xn–1 + + … + a1x + a0, лучше использовать функцию polyroots(a) вместо root. В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни как вещественные, так и комплексные. Коэффициенты полинома должны быть представлены в порядке возрастания степени х в векторе а длины n + 1.
Найти корни полинома x3 − 10x + 2
В вектор коэффициентов должны войти все коэффициенты, в том числе равные нулю:
|
|
2 |
|
|
|
−3.258 |
|
|
|
|
|
|
|||
v := |
|
−10 |
polyroots (v) = |
|
0.201 |
|
|
|
0 |
|
|
|
|||
|
|
1 |
|
|
|
3.057 |
|
|
|
|
|
|
|
|
|
Найти корни полинома с комплексными коэффициентами
x3 + (3 + 2i)x2 + (−4 + 6i) x − 8i
|
|
|
−8i |
|
|
|
|
|
|
Вектор коэффициентов |
v := |
|
−4 + 6i |
|
|
3 + 2i |
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Все корни, как вещественные, так и комплексные:
−4
polyroots (v) = −2i
1
Рис. 24. Использование функции polyroots
Пример нахождения корней полинома третьей степени с комплексными коэффициентами приведен на рис. 24.
60
