
маткад учебник
.pdf
5.3. Решение систем уравнений
Для решения систем уравнений выполните следующее:
задайте начальные приближения для всех неизвестных, входящих в систему уравнений;
наберите ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений. Убедитесь, что при этом вы не находитесь в текстовой области;
введите уравнения и неравенства в любом порядке ниже ключевого слова Given. Удостоверьтесь, что между левыми и правыми частями стоит символ =, напечатанный комбинацией клавиш [Ctrl+=] или выбранный из соответствующей палитры;
введите выражение, которое включает Find(z1, z2, z3, ...). Эта функция возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных.
Обычно для анализа решения удобно использовать иллюстрированный график. Пример решения систем уравнений приведен на рис. 25. Отметим, что в зависимости от численного значения начальных значений находится одно или другое решение. Между ключевыми словами Given и Find могут быть вставлены неравенства.
Блоки решения уравнений не могут быть вложены друг в друга. Каждый блок решения уравнений может иметь только одно ключевое слово Given и имя функции Find. Можно, однако, определить функцию f(x) := Find(x) в конце одного блока решения уравнений и затем использовать f(x) в другом блоке.
Причины, по которым Mathcad не может найти корни систем уравнений, принципиально те же, что и для функции root.
В инженерной практике часто приходится многократно решать системы уравнений и определять влияние параметра на решения. На рис. 26 приведен конкретный пример исследования зависимости максимального значения модуля функции комплексного переменного
A(ω )= W (iω ) ,
где W (iω )= |
|
k |
|
. |
|
T |
2 (iω )2 + 2T ξiω + 1 |
||||
|
|
||||
Напомним, что мнимая единица в Mathcad вводится как 1i. Максимальное значение функции A(ω ) определяется из условия
dA(ω ) =
dω
0.
61

Найти точки пересечения окружности и прямой
ψ := 0, |
π |
|
.. 2π |
|
|
x := −3, −2.9.. 3 |
|
|
||||||
|
|
|
|
|
||||||||||
20 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6 sin(ψ ) |
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
2−x |
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
0 |
2 |
4 |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
6 cos(ψ ) , x |
|
|
|
|
Решение 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Начальные значения |
|
|
x := 1 |
|
y := 1 |
|||||||||
Given |
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение окружности |
|
x2 + y2 = 6 |
|
|
||||||||||
Уравнение прямой |
|
|
x + y = 2 |
|
|
|||||||||
|
|
|
|
|
−0.414 |
|
|
|
|
|
|
|||
Find(x, y) = |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2.414 |
|
|
|
|
|
|
|||
Решение 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Начальные значения |
|
|
x := −1 |
|
y := 1 |
|||||||||
Given |
x2 + y2 = 6 |
|
x + y = 2 |
|
|
|
||||||||
|
|
|
|
|
−0.414 |
|
|
|
|
|
|
|||
Find(x, y) = |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2.414 |
|
|
|
|
|
|
|||
Рис. 25. Решение системы уравнений
62
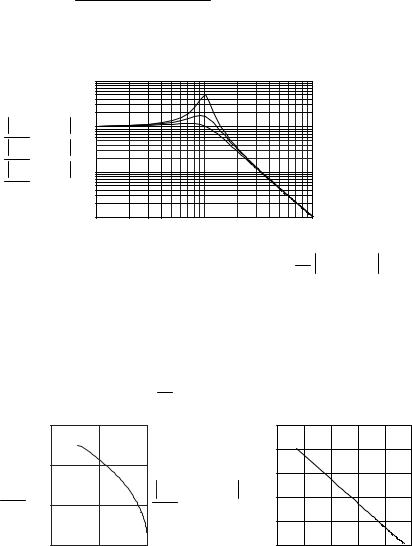
Дана функция комплексного переменного |
|
|
|
|
|
|
|
|
|
|
|
|
|||
( |
) |
|
1 |
ω |
:= 0.1, 0.2.. 10 |
|
|
|
T := 1 |
|
|||||
W ω , T, ξ := |
T2 (i ω )2 + 2 T ξ i ω + 1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
График модуля этой функции имеет максимальное значение, |
|
|
|
|
|
||||||||||
зависящее от параметра ξ: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
W(ω , T , 0.1) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W(ω , T , 0.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W(ω |
, T , 0.5) |
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.010.1 |
1 |
|
|
|
10 |
|
|
|
|
|
|
|
|
ω := 1 |
Given |
ω |
|
|
|
|
|
( |
|
) |
|
|
|||
Условие максимума |
d |
|
|
|
|
|
|||||||||
MaxMod(T, ξ) := Find(ω ) |
|
|
|
dω |
|
W |
|
ω , T , ξ |
|
= 0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Функция MaxMod(T, ξ)возвращает значение ω , соответсвующее |
|
|
|
|
|||||||||||
максимуму модуля комплексной функции при заданных T и ξ. |
|
|
|
|
|
||||||||||
Графики функций позволяют проанализировать размещение |
|
|
|
|
|
|
|||||||||
максимума на оси ω зависимость этого максимума от ξ. |
|
|
|
|
|
|
|
||||||||
m := 1.. 100 |
ξm := 0.0001 m2 |
ωmaxm := MaxMod(T , ξm) |
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
. |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
. |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
. |
3 |
|
|
|
|
|
|
|
|
|
|
ξm |
|
|
W(ω maxm ,T , ξm) 1 10 |
|
|
|
|
|
|
|
|
|
|
||
|
0.2 |
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0.8 |
|
|
1 |
–5 . –4 |
. |
|
|
|
|
|
|
|
|
|
0.6 |
|
|
. |
|
–3 |
0.01 |
|
|
0.1 |
1 |
||||
|
|
ω maxm |
|
|
1 10 |
1 10 |
|
1 10 |
ξm |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 26. Определение максимума модуля функции комплексного |
|
||||||||||||||
|
|
|
переменного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63 |
В приведенном примере всякий раз, когда вычисляется функция MaxMod, Mathcad подставляет заданные конкретные значения аргументов Т и ξ, решает уравнение относительно неизвестного w и возвращает найденное значение корня.
Приведенный пример включает в себя одно уравнение с одним неизвестным. Также возможно многократно решать и систему уравнений при различных значениях входящих в нее параметров. Однако в этом случае требуется проявить аккуратность при выводе результата, чтобы избежать сообщения об ошибке "нескалярная величина".
5.4. Решение дифференциальных уравнений
Mathcad имеет ряд встроенных функций, предназначенных для решения обыкновенных дифференциальных уравнений (ОДУ). При решении ОДУ искомой величиной является функция. При использовании любых методов численного интегрирования необходимо, чтобы были заданы по крайней мере следующие величины:
начальные условия; набор точек, в которых нужно найти решение;
само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан ниже.
Один из наиболее эффективных алгоритмов интегрирования ОДУ основан на численном методе Рунге – Кутты четвертого порядка. Функция, реализующая этот метод, имеет вид rkfixed(y, x1, x2, npoints, D).
Здесь:
у – вектор начальных условий размерности n, где n – порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений);
х1, х2 – граничные точки интервала, на котором ищется решение дифференциального уравнения. Начальные условия, заданные в векторе у, – это значение решения в точке х1;
npoints – число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed;
D(х, у) – функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций.
64
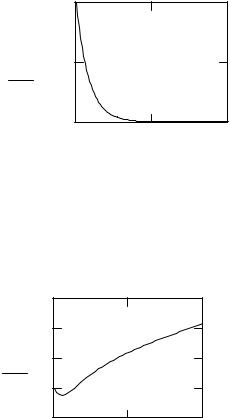
Решение уравнения y' + 3y = 0 |
|
|
|||
Начальное значение |
y0 := 4 |
|
|||
Определение функции, задающей производную y' = –3y: |
D(x, y) := −3 y0 |
||||
Вычисление решения в ста промежуточных точках на отрезке [0;4] |
|||||
Z := rkfixed(y , 0, 4, 100, D) |
|
|
|||
Построение графика решения |
i := 0.. rows(Z) − 1 |
|
|||
|
|
4 |
|
|
|
( 1 |
) |
2 |
|
|
|
Z |
i |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
|
|
|
0 |
|
||
|
|
|
( 0 |
) |
|
|
|
|
Z |
i |
|
|
|
|
|
|
|
Найти решение уравнения y' = –y 2 + x с начальным условием |
|||||
y(0) = 1 в пятидесяти промежуточных точках на отрезке [0;10] |
|||||
Начальное значение |
y0 := 1 |
|
|||
D(x, y) := −(y0)2 + x |
Z := rkfixed(y , 0, 10, 50, D) |
|
|||
Построение графика решения |
n := 0.. 50 |
|
|||
|
4 |
|
|
|
|
|
3 |
|
|
|
|
Zn ,1 |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
0 |
0 |
5 |
10 |
|
|
|
|
|||
|
|
|
Zn ,0 |
|
|
Рис. 27. Решение дифференциальных уравнений первого порядка |
|||||
65
На рис. 27 приведено решение двух дифференциальных решений первого порядка.
При решении дифференциальных уравнений более высоких порядков имеются следующие особенности:
вектор начальных значений у теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y′, y″, ..., y(n–1);
функция D является теперь вектором, содержащим n элементов:
|
y′(t) |
|
||
|
y′′(t) |
|
||
D(t, y) = |
|
... |
; |
|
|
|
|
||
|
y |
(n) |
|
|
|
|
(t) |
||
матрица, полученная в результате решения, содержит теперь n столбцов: первый для значений t, а оставшиеся –для значений у(t), y'(t), y"(t), ..., y(n–1)(t).
Пример, приведенный на рис. 28, показывает, как решить дифференциальное уравнение четвертого порядка
y( IV ) − 2k 2 y′′+ k 4 y = 0
c начальными условиями у(0) = 0, у′(0) = 1, у″(0) = 2, у′″(0) = 3.
На рис. 29 приведено решение системы дифференциальных уравнений первого порядка
x0′(t) = µx0 (t) − x1(t) −(x0 (t)2 + x1(t)2 )x0 (t),
x1′(t) = µx1(t) + x0 (t) −(x0 (t)2 + x1(t)2 )x1(t)
с начальными условиями x0(0) = 0, x1(0) = 1, и построен график зависимости x0(t) от x1(t).
66
k := 3 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Начальные условия |
y := |
|
1 |
|
|||
|
2 |
|
|||||
|
|
|
|
||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
y1 |
|
← |
Первая производная |
||
|
|
y2 |
|
|
|
|
|
D(t , y) := |
|
|
← |
Вторая производная |
|||
|
y |
3 |
|
← |
Третья производная |
||
|
|
|
|
||||
|
2k2 y2 − k4 y0 |
|
|
|
|||
|
|
|
← |
Четвертая производная |
|||
Z := rkfixed(y , 0, 5, 100, D)
Вычисление решения в ста промежуточных точках на отрезке [0;5]
|
|
t |
y(t) |
y'(t) |
y"(t) |
y'"(t) |
||
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
0.05 |
0.053 |
1.104 |
2.195 |
|
4.776 |
|
|
|
|
|
|
|
|
|
|
|
2 |
0.1 |
0.111 |
1.221 |
2.477 |
|
6.543 |
|
|
|
|
|
|
|
|
|
|
|
3 |
0.15 |
0.175 |
1.354 |
2.85 |
|
8.358 |
|
|
|
|
|
|
|
|
|
|
|
4 |
0.2 |
0.246 |
1.507 |
3.315 |
|
10.274 |
|
|
|
|
|
|
|
|
|
|
|
5 |
0.25 |
0.326 |
1.687 |
3.88 |
|
12.348 |
|
|
|
|
|
|
|
|
|
|
|
6 |
0.3 |
0.416 |
1.897 |
4.553 |
|
14.636 |
|
Z = |
|
|
|
|
|
|
|
|
7 |
0.35 |
0.516 |
2.144 |
5.348 |
|
17.198 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
0.4 |
0.631 |
2.434 |
6.279 |
|
20.101 |
|
|
|
|
|
|
|
|
|
|
|
9 |
0.45 |
0.761 |
2.775 |
7.365 |
|
23.417 |
|
|
|
|
|
|
|
|
|
|
|
10 |
0.5 |
0.909 |
3.174 |
8.629 |
|
27.225 |
|
|
|
|
|
|
|
|
|
|
|
11 |
0.55 |
1.079 |
3.641 |
10.097 |
|
31.616 |
|
|
|
|
|
|
|
|
|
|
|
12 |
0.6 |
1.275 |
4.187 |
11.802 |
|
36.694 |
|
|
|
|
|
|
|
|
|
|
|
13 |
0.65 |
1.499 |
4.826 |
13.78 |
|
42.577 |
|
|
|
|
|
|
|
|
|
|
|
14 |
0.7 |
1.759 |
5.571 |
16.075 |
|
49.401 |
|
|
|
|
|
|
|
|
|
|
|
15 |
0.75 |
2.059 |
6.439 |
18.738 |
|
57.321 |
|
|
|
|
|
|
|
|
|
|
Рис. 28. Решение дифференциального уравнения высокого порядка
67
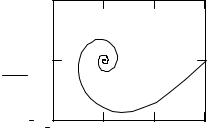
Решение системы двух нелинейных дифференциальных уравнений |
|
|
||||||||||
первого порядка |
|
|
|
|
|
|
|
|
|
|
|
|
µ := −0.2 |
Начальные условия |
|
|
0 |
|
|
|
|
|
|||
|
x := |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
µ x |
− x |
− |
(x )2 |
+ (x )2 |
|
x |
|
Первые производные |
|
|
0 |
1 |
|
0 |
1 |
|
0 |
|
||
D(t , x) := |
µ x |
|
− |
(x )2 |
+ (x )2 |
|
x |
|
||||
|
|
|
+ x |
|||||||||
|
|
|
|
|
1 |
0 |
|
0 |
1 |
|
1 |
|
Z := rkfixed(x, 0, 20, 100, D) |
|
n := 0.. 100 |
|
|
|
|
|
|
||||
График решения для t = 0..20 |
|
|
|
|
|
|
|
|
|
|||
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
Zn ,1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0.5 0.5 |
0 |
0.5 |
1 |
|
|
|
|
|
|
|
|
|
|
Zn ,2 |
|
|
|
|
|
|
|
|
|
|
Рис. 29. Решение системы дифференциальных уравнений |
|
|
||||||||||
|
|
|
первого порядка |
|
|
|
|
|
|
|
||
68
Решить систему: |
|
u" = 2v |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
v" = 4v - 2u |
|
|
|
|
|
|
|
||
с начальными условиями u(0) = 1.5, u'(0) = 1.5, v(0) = 1, v'(0) = 1. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение вектора начальных условий |
y := |
|
1.5 |
|
||||||
|
|
|
|
(u = y0, u' = y1, v = y2, v' = y3) |
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение вектора первых и вторых производных |
|
|
|
|
||||||||||
|
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2y2 |
|
|
|
|
|
|
|
|
|
D(x, y) := |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y3 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
4 y2 − 2 y0 |
|
Z := rkfixed(y , 0, 1, 100, D) |
|
|
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
|
u(x) |
u'(x) |
v(x) |
v'(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
1.5 |
1.5 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0.01 |
|
1.515 |
1.52 |
1.01 |
1.01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
0.02 |
|
1.53 |
1.54 |
1.02 |
1.02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
0.03 |
|
1.546 |
1.561 |
1.03 |
1.03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
0.04 |
|
1.562 |
1.582 |
1.041 |
1.041 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
0.05 |
|
1.578 |
1.603 |
1.051 |
1.051 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
0.06 |
|
1.594 |
1.624 |
1.062 |
1.062 |
|
|
|
|
|
Z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
0.07 |
|
1.61 |
1.645 |
1.073 |
1.072 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
0.08 |
|
1.627 |
1.667 |
1.083 |
1.083 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
0.09 |
|
1.643 |
1.688 |
1.094 |
1.094 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
0.1 |
|
1.66 |
1.71 |
1.105 |
1.105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
0.11 |
|
1.678 |
1.733 |
1.116 |
1.116 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
0.12 |
|
1.695 |
1.755 |
1.127 |
1.127 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
0.13 |
|
1.713 |
1.778 |
1.139 |
1.138 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
0.14 |
|
1.731 |
1.801 |
1.15 |
1.15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
0.15 |
|
1.749 |
1.824 |
1.162 |
1.161 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 30. Решение системы дифференциальных уравнений второго порядка
69
Рис. 30 показывает, как поступать при решении систем уравнений порядка выше первого.
Функция rkfixed возвращает матрицу, в которой:
первый столбец содержит точки, в которых должны быть найдены решения и их производные;
остальные столбцы содержат значения решений и их производных, соответствующие точкам их первого столбца. Порядок, в котором появляются решение и их производные, повторяет порядок их расположения в функции D(x, y) и векторе начальных условий у.
Функция kfixed, описанная выше, использует универсальный метод для решения уравнений с постоянным шагом. Шаг численного интегрирования определяется интервалами х2 – х1 и количеством промежуточных точек npoints. Измененяя шаг численного интегрирования, можно в значительных пределах менять точность решения задачи.
Система дифференциальных уравнений может иметь некоторые специфические свойства, используя которые, можно решать ее более точно и быстро. Когда известно, что решение является гладкой функцией, лучше использовать функцию Bulstoer(y, x1, x2, npoints, D), где аргументы имеют тот же смысл, что в функции rkfixed. В отличие от функции rkfixed, функция Bulstoer использует численный метод Bulirsch-Stoer.
Если искомая функция на отрезке [х1; х2] значительно меняет свой наклон, то эффективнее использовать функцию Rkadapt(y, x1, x2, npoints, D). Эта функция проверяет, как быстро меняется приближенное решение и адаптирует соответственно размер шага. Адаптивный контроль шага дает возможность функции Rkadapt вычислять значение приближенного решения на более мелкой сетке в тех областях, где оно меняется быстро, и на более крупной – в тех областях, где оно меняется медленно. Это позволяет повысить точность, и сократить время требуемое для решения уравнения.
Существует ряд систем дифференциальных уравнений, решение которых содержит быстрые осциллирующие процессы и медленные составляющие. Типичным видом таких систем являются дифференциальные уравнения, описывающие поведение гироскопических приборов с учетом нутационных колебаний и прецессионного движения. Для решения таких задач в Mathcad используются функции stiffb(y, x1, x2, npoints, D, J), stiffr(y, x1, x2, npoints, D, J).
В первой функции используется Bulirsch-Stoer метод для решения жестких систем, а во второй функции Rosenbrock метод. Использова-
70
