MAiu9

matemati~eskij analiz - 1 SEM. — DLQ iu9

dALEE SSYLKI NA U^EBNIKI:

[z]: zORI^ w.a. mATEMATI^ESKIJ ANALIZ. ~. I. - m.: nAUKA, 1981. - 544S.

[m]: mOROZOWA w.d. wWEDENIE W ANALIZ. - m.: iZD-WO mgtu, 1996. - 331S.

[iW]: iWANOWA e.e. dIFFERENCIALXNOE IS^ISLENIE FUNKCIJ ODNOGO PEREMENNO -

GO. - m.: iZD-WO mgtu, 1998. - 408S.

[k]: kUDRQWCEW l.d. kURS MATEMATI^ESKOGO ANALIZA. t. I. - m.: wYS[AQ [KOLA,

1981.

[as~]: aRHIPOW g.i., sADOWNI^IJ w.a., ~UBARIKOW w.n. lEKCII PO MATEMATI- ^ESKOMU ANALIZU / pOD RED. w.a. sADOWNI^EGO. - m.: wYS[. [K., 1999. - 695S.

1|LEMENTY TEORII MNOVESTW

sM. [z, STR. 5–9].

1.1mNOVESTWA

mNOVESTWO — \TO SOWOKUPNOSTX OPREDELENNYH \LEMENTOW , SWQZANNYH KAKIM–LIBO OB]IM SWOJSTWOM.

pRIMER 1. N — MNOVESTWO NATURALXNYH ^ISEL; Z — MNOVESTWO CELYH ^ISEL;

Q — MNOVESTWO RACIONALXNYH ^ISEL; R — MNOVESTWO DEJSTWITELXNYH ^ISEL.

mNOVESTWO, KOTOROE NE IMEET NI ODNOGO \LEMENTA, NAZYWAETSQ PUSTYM MNO- VESTWOM I OBOZNA^AETSQ .

tOT FAKT, ^TO \LEMENT a PRINADLEVIT MNOVESTWU A, ZAPISYWAETSQ W WIDE a A ILI A 3 a, A TO, ^TO NE PRINADLEVIT — W WIDE a 6A. mNOVESTWA BUDEM, KAK PRA- WILO, OBOZNA^ATX BOLX[IMI BUKWAMI LATINSKOGO ALFAWITA , A IH \LEMENTY — MA- LYMI, HOTQ INOGDA OT \TOGO SOGLA[ENIQ PRIDETSQ OTSTUPATX , TAK KAK \LEMENTAMI NEKOTOROGO MNOVESTWA MOGUT BYTX DRUGIE MNOVESTWA .

CIMWOLY (KON_@NKCIQ), (DIZ_@NKCIQ), (IMPLIKACIQ) I

(\KWIWALENTNOSTX) BUDEM PONIMATX KAK SIMWOLY, ZAMENQ@]IE SLOWOSO^ETANIQ:

— ”I”;

— ”ILI”;

— ”ESLI . . . , TO” ILI ”WLE^ET”;

— ”RAWNOSILXNO” ILI ”TOGDA I TOLXKO TOGDA, KOGDA”, ILI ”ESLI I TOLXKO ESLI”.

dWA MNOVESTWA A I B S^ITA@T RAWNYMI, ESLI L@BOJ \LEMENT x MNOVESTWA A QWLQETSQ \LEMENTOM MNOVESTWA B I NAOBOROT, T.E. a A a B. iZ PRIWEDENNOGO OPREDELENIQ RAWNYH MNOVESTW SLEDUET , ^TO MNOVESTWO POLNOSTX@ OPREDELQETSQ SWOIMI \LEMENTAMI.

1

rASSMOTRIM SPOSOBY ZADANIQ KONKRETNYH MNOVESTW. dLQ KONE^NOGO MNOVE- STWA, ^ISLO \LEMENTOW KOTOROGO OTNOSITELXNO NEWELIKO , MOVET BYTX ISPOLXZOWAN

SPOSOB NEPOSREDSTWENNOGO PERE^ISLENIQ \LEMENTOW. |LEMENTY KONE^NOGO MNO- VESTWA PERE^ISLQ@T W FIGURNYH SKOBKAH W PROIZWOLXNOM FIKSIROWANNOM PORQDKE {1; 3; 5}. pOD^ERKNEM, ^TO POSKOLXKU MNOVESTWO POLNOSTX@ OPREDELENO SWOIMI \LE -

MENTAMI, TO PRI ZADANII KONE^NOGO MNOVESTWA PORQDOK , W KOTOROM PERE^ISLENY EGO \LEMENTY, NE IMEET ZNA^ENIQ. pO\TOMU ZAPISI {1; 3; 5}, {3; 1; 5}, {5; 3; 1} I T.D. WSE ZADA@T ODNO I TO VE MNOVESTWO. kROME TOGO, INOGDA W ZAPISI MNOVESTW IS- POLXZU@T POWTORENIQ \LEMENTOW. bUDEM S^ITATX, ^TO ZAPISX {1; 3; 3; 5; 5} ZADAET TO VE SAMOE MNOVESTWO, ^TO I ZAPISX {1; 3; 5}.

w OB]EM SLU^AE DLQ KONE^NOGO MNOVESTWA ISPOLXZU@T FORMU ZAPISI {a1; . . . ; an}. kAK PRAWILO, PRI \TOM IZBEGA@T POWTORENIJ \LEMENTOW. tOGDA KONE^NOE MNOVE- STWO, ZADANNOE ZAPISX@ {a1; . . . ; an}, SOSTOIT IZ n \LEMENTOW. eGO NAZYWA@T TAKVE

n–\LEMENTNYM MNOVESTWOM.

oDNAKO SPOSOB ZADANIQ MNOVESTWA PUTEM NEPOSREDSTWENNOGO PERE^ISLENIQ EGO \LEMENTOW PRIMENIM W WESXMA UZKOM DIAPAZONE KONE^NYH MNOVESTW . nAIBOLEE OB-

]IM SPOSOBOM ZADANIQ KONKRETNYH MNOVESTW QWLQETSQ UKAZANIE NEKOTOROGO SWOJ - STWA, KOTORYM DOLVNY OBLADATX WSE \LEMENTY OPISYWAEMOGO MNOVESTWA , I TOLXKO ONI.

|TA IDEQ REALIZUETSQ SLEDU@]IM OBRAZOM. pUSTX RASSMATRIWA@TSQ TOLXKO MNOVESTWA, QWLQ@]IESQ ^ASTX@ NEKOTOROGO MNOVESTWA U. sWOJSTWO, KOTORYM OBLADA@T ISKL@^ITELXNO \LEMENTY DANNOGO MNOVESTWA A, OBOZNA^IM ^EREZ P (x) I NAZOWEM HARAKTERISTI^ESKIM SWOJSTWOM ILI KOLLEKTIWIZIRU@]IM SWOJ-

STWOM. mNOVESTWO, ZADANNOE \TIM SWOJSTWOM, ZAPISYWAETSQ W SLEDU@]EJ FORME:

A = {x U : P (x)}.

pRIMER 2: A = {x N: x — DELITELX 36} = {1, 2, 3, 4, 6, 9, 12, 18, 36}.

pRIMER 3. pOPYTKA OPREDELITX MNOVESTWO Y = {X : X / X} WSEH MNOVESTW, KOTORYE NE QWLQ@TSQ \LEMENTAMI SAMIH SEBQ , PRIWODIT K PROTIWORE^I@. w SAMOM DELE, \TO MNOVESTWO NE PUSTO. nAPRIMER, MNOVESTWO R WSEH DEJSTWITELXNYH ^I- SEL NE ESTX DEJSTWITELXNOE ^ISLO. pUSTX Y NE QWLQETSQ \LEMENTOM SAMOGO SEBQ, T.E. Y / Y . tOGDA, POSKOLXKU Y ESTX MNOVESTWO WSEH MNOVESTW, NE QWLQ@]IHSQ \LEMENTAMI SAMIH SEBQ, Y Y . w TO VE WREMQ, ESLI Y Y , DOLVNO WYPOLNQTXSQ Y / Y . sLEDOWATELXNO, MY DOKAZALI, ^TO Y / Y Y Y ! |TO PROTIWORE- ^IE PRIWODIT K PARADOKSU, NAZYWAEMOMU PARADOKSOM rASSELA. oN PRIWODITSQ INOGDA W TAKOJ ”SKAZO^NO-[UTLIWOJ” REDAKCII: ”w NEKOTOROJ DEREWNE VIWET BRA- DOBREJ, KOTORYJ PO DOLGU SLUVBY DOLVEN BRITX TEH I TOLXKO TEH , KTO NE BREET SEBQ SAM”. bRADOBREJ OKAZYWAETSQ W NEZAWIDNOM POLOVENII : ESLI ON NE BUDET SE- BQ BRITX, TO TOT^AS OKAVETSQ, ^TO ON DOLVEN SEBQ BRITX, A SLEDUQ NEUMOLIMOJ INSTRUKCII, ON NEMEDLENNO DOLVEN PREKRATITX BRITXSQ, IBO ON BUDET BRITX SEBQ SAM, ^TO ZAPRE]ENO.

pARADOKS rASSELA POKAZYWAET, ^TO INTUITIWNOE PONIMANIE MNOVESTWA POZWO - LQET TRAKTOWATX IDE@ MNOVESTWA NASTOLXKO [IROKO I RASPLYW^ATO , ^TO MOVET PRIWESTI K PROTIWORE^IQM. ~TOBY IZBEVATX TAKIH PROTIWORE^IJ, WWODQT PONQTIE UNIWERSALXNOGO MNOVESTWA U. i PREDPOLAGA@T, ^TO RASSMATRIWA@TSQ TOLXKO TAKIE MNOVESTWA, \LEMENTY KOTORYH QWLQ@TSQ I \LEMENTAMI MNOVESTWA U.

2

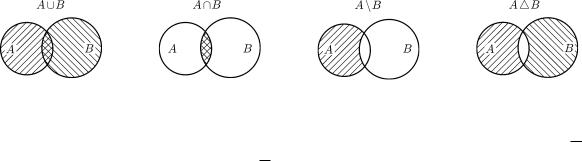
1.2oPERACII NAD MNOVESTWAMI

dLQ L@BYH DWUH MNOVESTW A I B OPREDELENY NOWYE MNOVESTWA, NAZYWAEMYE OB_-

EDINENIEM, PERESE^ENIEM, RAZNOSTX@ I SIMMETRI^ESKOJ RAZNOSTX@:

wWEDENNYE MNOVESTWA PROILL@STRIRUEM DIAGRAMMAMI |JLERA — wENNA. dIA- GRAMMAMI |JLERA — wENNA NAZYWA@T FIGURY, USLOWNO IZOBRAVA@]IE MNO- VESTWA. iLL@STRACIQ WWEDENNYH MNOVESTW PREDSTAWLENA NA RIS . 1 (ONI OTME^ENY [TRIHOWKOJ).

rIS. 1

fIKSIRUQ UNIWERSALXNOE MNOVESTWO U, MY MOVEM OPREDELITX DOPOLNENIE A MNOVESTWA A SLEDU@]IM OBRAZOM: A = U \A. iTAK, DOPOLNENIE MNOVESTWA A — \TO MNOVESTWO WSEH \LEMENTOW UNIWERSALXNOGO MNOVESTWA , NE PRINADLEVA]IH A. gOWORQT, ^TO B ESTX PODMNOVESTWO MNOVESTWA A, ESLI WSQKIJ \LEMENT B ESTX \LEMENT A. dLQ OBOZNA^ENIQ ISPOLXZU@T ZAPISX: B A. gOWORQT TAKVE, ^TO B

SODERVITSQ W A, B WKL@^ENO W A, A WKL@^AET B, IMEET MESTO WKL@^ENIE

B A. s^ITA@T, ^TO PUSTOE MNOVESTWO ESTX PODMNOVESTWO L@BOGO MNOVESTWA I , ESLI FIKSIROWANO NEKOTOROE UNIWERSALXNOE MNOVESTWO , KAVDOE RASSMATRIWAEMOE MNOVESTWO ESTX EGO PODMNOVESTWO.

sOPOSTAWLQQ OPREDELENIE PODMNOVESTWA I OPREDELENIE RAWENSTWA MNOVESTW , MY WIDIM, ^TO MNOVESTWO A RAWNO MNOVESTWU B TOGDA I TOLXKO TOGDA, KOGDA A ESTX PODMNOVESTWO B I NAOBOROT, T.E.

A = B (A B I B A).

pOSLEDNQQ FORMULA QWLQETSQ OSNOWOJ DLQ POSTROENIQ DOKAZATELXSTW O RAWEN - STWE MNOVESTW. eE PRIMENENIE SOSTOIT W SLEDU@]EM. ~TOBY DOKAZATX RAWENSTWO DWUH MNOVESTW X I Y , T.E. ^TO X = Y , DOSTATO^NO DOKAZATX DWA WKL@^ENIQ X Y I Y X, T.E. DOKAZATX, ^TO IZ PREDPOLOVENIQ x X (DLQ PROIZWOLXNOGO x) SLEDU- ET, ^TO x Y , I, NAOBOROT, IZ PREDPOLOVENIQ x Y SLEDUET, ^TO x X. tAKOJ ME- TOD DOKAZATELXSTWA TEORETIKO-MNOVESTWENNYH RAWENSTW NAZYWA@T METODOM DWUH WKL@^ENIJ. pRIMERY PRIMENENIQ \TOGO METODA MY DADIM POZVE.

eSLI B A, NO B 6= A, TO PI[UT B A I B NAZYWA@T STROGIM PODMNO-

VESTWOM (ILI SOBSTWENNYM PODMNOVESTWOM) MNOVESTWA A, A SIMWOL — SIMWOLOM STROGOGO WKL@^ENIQ.

wWEDENNYE WY[E OPERACII NAD MNOVESTWAMI OBLADA@T SLEDU@]IMI SWOJSTWA -

MI:

1. A B = B A;

3

2.A ∩ B = B ∩ A;

3.A (B C) = (A B) C;

4.A ∩ (B ∩ C) = (A ∩ B) ∩ C;

5.A ∩ (B C) = (A ∩ B) (A ∩ C);

6.A (B ∩ C) = (A B) ∩ (A C);

7.A B = A ∩ B;

8.A ∩ B = A B;

9.A = A;

10.A ∩ = ;

11.A ∩ U = A;

12.A U = U;

13.A A = U;

14.A ∩ A = ;

15.A A = A;

16.A ∩ A = A;

17.A = A;

18.A \ B = A ∩ B;

19.A 4 B = (A B) \ (A ∩ B);

20.(A 4 B) 4 C = A 4(B 4 C);

21.A 4 B = B 4 A;

22.A ∩ (B 4 C) = (A ∩ B) 4(A ∩ C).

kAVDOE IZ NAPISANNYH WY[E RAWENSTW, WERNOE DLQ L@BYH WHODQ]IH W NIH MNO-

VESTW, ^ASTO NAZYWA@T TEORETIKO–MNOVESTWENNYM TOVDESTWOM. l@BOE IZ NIH MOVET BYTX DOKAZANO METODOM DWUH WKL@^ENIJ .

zADA^A 1. dOKAVITE \TIM METODOM TOVDESTWO 19.

dLQ ILL@STRACII TEORETIKO–MNOVESTWENNYH TOVDESTW ISPOLXZU@TSQ DIAGRAM - MY |JLERA — wENNA.

pRIMER 4. rASSMOTRIM SWOJSTWO 8, KOTOROE NAZYWAETSQ WTORYM ZAKONOM DE mORGANA. uNIWERSALXNOE MNOVESTWO BUDEM IZOBRAVATX PRQMOUGOLXNIKOM Ω. zA[TRIHOWANNAQ NA RIS. 2,A OBLASTX IZOBRAVAET MNOVESTWO A ∩ B, A NEZA[TRI- HOWANNAQ ^ASTX PRQMOUGOLXNIKA Ω (WNE[NQQ PO OTNO[ENI@ K ZA[TRIHOWANNOJ)

4

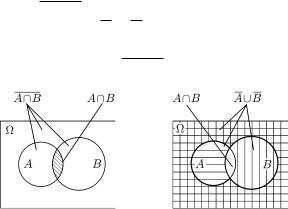
SOOTWETSTWUET MNOVESTWU A ∩ B. nA RIS. 2,B ^ASTI PRQMOUGOLXNIKA Ω, ZA[TRIHO-

WANNYE WERTIKALXNO I MNOVESTWU A B OTWE^AET OBLASTX, ZA[TRIHOWANNAQ HOTQ BY ODNIM IZ UKAZANNYH SPOSOBOW. oNA SOWPADAET S OBLASTX@, NE ZA[TRIHOWANNOJ

NA RIS. 2,A I OTWE^A@]EJ MNOVESTWU A ∩ B, ^TO ILL@STRIRUET SWOJSTWO 8.

A B rIS. 2

pOMIMO METODA DWUH WKL@^ENIJ DLQ DOKAZATELXSTWA TEORETIKO -MNOVESTWENNYH TOVDESTW MOGUT BYTX ISPOLXZOWANY DRUGIE METODY , NAPRIMER METOD HARAKTE-

RISTI^ESKIH FUNKCIJ.

kROME TOGO, TEORETIKO-MNOVESTWENNYE TOVDESTWA MOVNO DOKAZYWATX , ISPOLX- ZUQ RANEE DOKAZANNYE TOVDESTWA DLQ PREOBRAZOWANIQ LEWOJ ^ASTI K PRAWOJ ILI NAOBOROT. tAKOJ METOD DOKAZATELXSTWA ^ASTO NAZYWA@T METODOM \KWIWALENT-

NYH PREOBRAZOWANIJ.

zADA^A 2. dOKAVITE \TIM METODOM TOVDESTWO 22, POLXZUQSX TOVDESTWAMI 1–19.

2|LEMENTY TEORII MNOVESTW II

sM. [z, STR. 9–22].

2.1oTOBRAVENIQ MNOVESTW

oTOBRAVENIE (FUNKCIQ) f IZ MNOVESTWA A W MNOVESTWO B S^ITAETSQ ZADANNYM, ESLI KAVDOMU \LEMENTU x A SOPOSTAWLEN EDINSTWENNYJ \LEMENT y B.

oTOBRAVENIE f IZ MNOVESTWA A W MNOVESTWO B OBOZNA^A@T ZAPISX@ f : A → B. mNOVESTWO A NAZYWA@T OBLASTX@ OPREDELENIQ FUNKCII f I OBOZNA^A@T D(f),

MNOVESTWO B — OBLASTX@ ZNA^ENIJ FUNKCII f, \LEMENT x X — ARGUMEN- TOM FUNKCII, A \LEMENT y Y — ZAWISIMYM PEREMENNYM. |LEMENT y B,

KOTORYJ OTOBRAVENIEM f SOPOSTAWLQETSQ \LEMENTU x A, NAZYWA@T OBRAZOM \LEMENTA x PRI OTOBRAVENII f ILI ZNA^ENIEM FUNKCII f W TO^KE x I OBO-

ZNA^A@T f(x). pRI \TOM \LEMENT x A NAZYWA@T PROOBRAZOM \LEMENTA y PRI OTOBRAVENII f.

CIMWOLY (KWANTOR OB]NOSTI), (KWANTOR SU]ESTWOWANIQ) I ! BUDEM PONIMATX KAK SIMWOLY, ZAMENQ@]IE SLOWOSO^ETANIQ:

1. wYRAVENIE ”DLQ WSQKOGO \LEMENTA x MNOVESTWA E” ZAPISYWA@T W WIDE x E. |TA ZAPISX OZNA^AET, ^TO UTWERVDENIE, SLEDU@]EE ZA NEJ, BUDET WYPOLNENO DLQ PROIZWOLXNOGO \LEMENTA MNOVESTWA E. zAPISX x1, x2, . . ., xn E OZNA^AET: ”KAKOWY BY NI BYLI \LEMENTY x1, x2, . . ., xn MNOVESTWA E”.

5

2. wYRAVENIE ”SU]ESTWUET PO KRAJNEJ MERE ODIN \LEMENT MNOVESTWA E, TAKOJ, ^TO . . . ” ZAPISYWA@T x E: . . . wSE, ^TO SLEDUET ZA \TOJ ZAPISX@, WYPOLNQETSQ HOTQ BY DLQ ODNOGO \LEMENTA MNOVESTWA E. nAOBOROT, @x E: . . . OZNA^AET, ^TO WSE SLEDU@]EE DALEE NE WYPOLNQETSQ NI DLQ ODNOGO \LEMENTA IZ E.

3. wYRAVENIE ”SU]ESTWUET ODIN I TOLXKO ODIN \LEMENT IZ E, TAKOJ, ^TO . . . ” ZAPISYWA@T W WIDE ! x E: . . . zAPISX x1, x2, . . ., xn E: . . . OZNA^AET: ”SU]ESTWU@T TAKIE \LEMENTY x1, x2, . . ., xn MNOVESTWA E, ^TO . . . ”.

rASSMOTRIM OTOBRAVENIE f : A → B. oBRAZOM PODMNOVESTWA C A NAZY- WA@T MNOVESTWO

f(C) = {y B : x C f(x) = y}.

pROOBRAZOM PODMNOVESTWA D B NAZYWA@T MNOVESTWO

f−1(D) = {x A: f(x) D}.

oTOBRAVENIE f MNOVESTWA A W SEBQ NAZYWA@T TOVDESTWENNYM, ESLI f(x) = x PRI WSEH x IZ A. oTOBRAVENIE f : A → B NAZYWA@T IN_EKTIWNYM (IN_EKCIEJ), ESLI IZ RAWENSTWA f(x) = f(x0) SLEDUET x = x0. nAZYWA@T S@R_EKTIWNYM (S@R_- EKCIEJ), ESLI EGO OBLASTX ZNA^ENIJ SOWPADAET SO WSEM MNOVESTWOM B (f(A) = B). i NAKONEC, NAZYWA@T BIEKTIWNYM (BIEKCIEJ), ESLI ONO ODNOWREMENNO IN_EK- TIWNO I S@R_EKTIWNO.

tAKIM OBRAZOM, ESLI OTOBRAVENIE f : A → B BIEKTIWNO, TO KAVDOMU \LEMENTU MNOVESTWA A OTWE^AET EDINSTWENNYJ \LEMENT MNOVESTWA B I NAOBOROT. tOGDA GOWORQT, ^TO MNOVESTWA A I B NAHODQTSQ MEVDU SOBOJ WO WZAIMNO ODNOZNA^NOM SOOTWETSTWII.

dLQ FUNKCIJ f : A → B I g : A → B W SLU^AE B R WWODQT ARIFMETI^ESKIE OPERACII:

(f + g)(x) = f(x) + g(x), (fg)(x) = f(x)g(x), (f −g)(x) = f(x) −g(x), fg (x) = fg((xx)),

PRI \TOM OPERACIQ DELENIQ OPREDELQETSQ TOLXKO W TO^KAH x, GDE g(x) 6= 0.

mNOVESTWO WSEH OTOBRAVENIJ IZ A W B BUDEM OBOZNA^ATX KAK BA. mNOVESTWO WSEH PODMNOVESTW MNOVESTWA U NAZYWA@T BULEANOM MNOVESTWA U I OBOZNA^A@T

2U :

2U = {A: A U}.

hARAKTERISTI^ESKAQ FUNKCIQ χA MNOVESTWA A U ESTX FUNKCIQ, OTO-

BRAVA@]AQ UNIWERSALXNOE MNOVESTWO U W DWUH\LEMENTNOE MNOVESTWO {0; 1}:

iZ OPREDELENIJ WYTEKAET SPRAWEDLIWOSTX TOVDESTW

STWU A U EGO HARAKTERISTI^ESKU@ FUNKCI@ χA, ESTX BIEKCIQ.

6

zADA^A 1. dOKAVITE TEOREMU.

mETOD HARAKTERISTI^ESKIH FUNKCIJ DOKAZATELXSTWA SPRAWEDLIWOSTI TEORETI -

KO–MNOVESTWENNYH TOVDESTW ZAKL@^AETSQ W WYRAVENII HARAKTERISTI^ESKIH FUNK - CIJ OBEIH ^ASTEJ TOVDESTWA ^EREZ HARAKTERISTI^ESKIE FUNKCII WHODQ]IH W NEGO MNOVESTW. pRI \TOM ISPOLXZU@TSQ UKAZANNYE SWOJSTWA HARAKTERISTI^ESKIH FUNK -

CIJ. pO TEOREME 1 TOVDESTWO WERNO TOGDA I TOLXKO TOGDA, KOGDA HARAKTERISTI^E- SKIE FUNKCII LEWOJ I PRAWOJ ^ASTEJ SOWPADA@T .

fUNKCIQ g ESTX OBRATNAQ K FUNKCII f, ESLI x = g(y) y = f(x). oBOZNA^ENIQ: g = f−1.

pUSTX f : A → B, g : C → D, B C. tOGDA OPREDELENO OTOBRAVENIE g ◦f : A → D, (g◦f)(x) = g(f(x)), KOTOROE NAZYWA@T KOMPOZICIEJ OTOBRAVENIJ (SLOVNOJ FUNKCIEJ) f I g.

2.2sEMEJSTWA MNOVESTW

pUSTX U — UNIWERSALXNOE MNOVESTWO, I — PROIZWOLXNOE MNOVESTWO (NIKAK NE SWQZANNOE S U), A KAVDOMU \LEMENTU i I ODNOZNA^NO SOPOSTAWLENO PODMNOVESTWO

Ai U. tOGDA GOWORQT, ^TO ZADANO (INDEKSIROWANNOE) SEMEJSTWO MNOVESTW mNOVESTWO I NAZYWA@T MNOVESTWOM INDEKSOW, A MNOVESTWA

TAMI SEMEJSTWA (Ai)i I .

tAKIM OBRAZOM, SEMEJSTWO (Ai)i I OPREDELENO, ESLI ZADANO OTOBRAVENIE : I → 2U . w SLU^AE I = N POLU^AEM POSLEDOWATELXNOSTX MNOVESTW , ILI S^ETNOE SE-

MEJSTWO MNOVESTW; ESLI MNOVESTWO I KONE^NO, POLU^AEM KONE^NOE SEMEJSTWO MNOVESTW.

oPERACII OB_EDINENIQ I PERESE^ENIQ MNOVESTW MOVNO RASPROSTRANITX NA PRO - IZWOLXNYE SEMEJSTWA MNOVESTW.

1. oB_EDINENIE SEMEJSTWA MNOVESTW:

[

Ai = {x: i x Ai}.

i I

2. pERESE^ENIE SEMEJSTWA MNOVESTW:

\

Ai = {x: i x Ai}.

i I

sPRAWEDLIWY SLEDU@]IE TOVDESTWA:

7

SS

1. A i I Bi = i I (A Bi);

2. A ∩ Ti I Bi = Ti I (A ∩ Bi);

3. A ∩ Si I Bi = Si I (A ∩ Bi);

TT

4. A i I Bi = i I (A Bi);

ST

5. i I Ai = i I Ai;

TS

6. i I Ai = i I Ai.

|TI SWOJSTWA NETRUDNO DOKAZATX METODOM DWUH WKL@^ENIJ .

zADA^A 5. dOKAVITE WTOROE I TRETXE TOVDESTWA.

2.3dEKARTOWY PROIZWEDENIQ

pUSTX A I B — PROIZWOLXNYE MNOVESTWA. uPORQDO^ENNAQ PARA NA MNOVESTWAH A I B, OBOZNA^AEMAQ ZAPISX@ (a; b), OPREDELQETSQ \LEMENTAMI a A I b B, A TAKVE PORQDKOM, W KOTOROM ONI ZAPISANY. eSLI A = B, TO GOWORQT OB UPORQDO^ENNOJ PARE NA MNOVESTWE A. dWE UPORQDO^ENNYE PARY (a; b) I (a0; b0) NA MNOVESTWAH A I B NAZYWA@T RAWNYMI, ESLI a = a0 I b = b0.

uPORQDO^ENNU@ PARU (a; b) NE SLEDUET SWQZYWATX S MNOVESTWOM {a; b}, TAK KAK UPORQDO^ENNAQ PARA HARAKTERIZUETSQ NE TOLXKO SOSTAWOM , NO I PORQDKOM \LEMENTOW W NEJ.

pROSTEJ[IJ I WAVNEJ[IJ PRIMER UPORQDO^ENNYH PAR NAT W ANALITI^ESKOJ GEOMETRII.

oBOB]ENIEM PONQTIQ UPORQDO^ENNOJ PARY QWLQETSQ UPORQDO^ENNYJ n–NABOR ILI KORTEV. gOWORQT TAKVE: UPORQDO^ENNAQ n–KA (NAPRIMER, UPORQDO^ENNAQ TROJKA, ^ETWERKA, PQTERKA I T.D.). w OTLI^IE OT KONE^NOGO MNOVESTWA {a1; . . . ; an} KORTEV (a1; . . . ; an) NA MNOVESTWAH A1, . . . , An HARAKTERIZUETSQ NE TOLXKO WHODQ- ]IMI W NEGO \LEMENTAMI a1 A1, . . . , an An, NO I PORQDKOM, W KOTOROM ONI PERE^ISLQ@TSQ.

dWA KORTEVA A1, . . . , An RAWNY, ESLI

ai = bi, i = 1, . . . , n.

~ISLO n NAZYWAETSQ DLINOJ KORTEVA (ILI RAZMERNOSTX@ KORTEVA), A \LEMENT ai — i–J PROEKCIEJ (KOMPONENTOJ) KORTEVA. dLQ DWUH KORTEVEJ ODINA-

KOWOJ RAZMERNOSTI IH KOMPONENTY S ODINAKOWYMI NOMERAMI NAZYWA@T ODNOIMENNYMI KOMPONENTAMI. oPREDELENIE RAWENSTWA KORTEVEJ MOVNO PEREFORMULIRO - WATX TAK: DWA KORTEVA ODINAKOWOJ RAZMERNOSTI RAWNY TOGDA I TOLXKO TOGDA , KOGDA IH ODNOIMENNYE KOMPONENTY SOWPADA@T.

mNOVESTWO WSEH KORTEVEJ DLINY n NA MNOVESTWAH A1, . . . , An NAZYWA@T DE-

KARTOWYM (PRQMYM) PROIZWEDENIEM MNOVESTW A1, . . . , An I OBOZNA^A@T

A1 × · · · × An.

tAKIM OBRAZOM,

A1 × · · · × An = {(a1; . . . ; an) : a1 A1, . . . , an An}.

8

eSLI WSE MNOVESTWA Ai, i = 1, . . . , n, RAWNY MEVDU SOBOJ, TO UKAZANNOE DEKARTOWO PROIZWEDENIE NAZYWA@T n–J DEKARTOWOJ STEPENX@ MNOVESTWA A I OBOZNA^A@T An. w ^ASTNOSTI, PRI n = 2 POLU^AEM DEKARTOW KWADRAT, A PRI n = 3 —

DEKARTOW KUB MNOVESTWA A.

pO OPREDELENI@ POLAGA@T, ^TO PERWAQ DEKARTOWA STEPENX L@BOGO MNOVESTWA A ESTX SAMO MNOVESTWO A, T.E. A1 = A.

dEKARTOWO PROIZWEDENIE IMEET SLEDU@]IE SWOJSTWA :

1.A × (B C) = (A × B) (A × C);

2.A × (B ∩ C) = (A × B) ∩ (A × C);

3.A × = × A = .

|TI SWOJSTWA NETRUDNO DOKAZATX METODOM DWUH WKL@^ENIJ. iZ POSLEDNEGO TOVDESTWA WYTEKAET, ^TO PUSTOE MNOVESTWO PRI POSTROENII DEKARTOWYH PROIZWE - DENIJ MNOVESTW IGRAET TU VE ROLX, ^TO I NULX PRI UMNOVENII ^ISEL.

kAVDOE OTOBRAVENIE f : A → B ODNOZNA^NO OPREDELQET MNOVESTWO UPORQDO^EN - NYH PAR {(x, y) A × B : x A, y = f(x)}, NAZYWAEMOE GRAFIKOM OTOBRAVE-

NIQ f.

gRAFIK OBRATNOJ FUNKCII f−1 POLU^AETSQ IZ GRAFIKA FUNKCII f ZERKALXNYM OTRAVENIEM OTNOSITELXNO PRQMOJ y = x.

pRIMER 1. arcsin x.

3~ISLOWYE MNOVESTWA

sM. [z, STR. 33–55, 68–70], [as~, STR. 27–28], [k, STR. 43].

3.1mNOVESTWO DEJSTWITELXNYH ^ISEL

dADIM GEOMETRI^ESKU@ INTERPRETACI@ WE]ESTWENNYH ^ISEL . gOWORQT, ^TO NA PRQ- MOJ ZADANA SISTEMA OTS^ETA, ESLI NA \TOJ PRQMOJ FIKSIROWANY DWE RAZLI^NYE TO^KI (TO^KI O I e NA RIS. 3). tO^KU O NAZYWA@T NA^ALOM OTS^ETA, A DLINA OTREZKA Oe ZADAET EDINICU MAS[TABA, T.E. POLAGAEM: |Oe| = 1. pRQMU@ S ZADANNOJ SISTE- MOJ OTS^ETA NAZYWA@T KOORDINATNOJ OSX@. eE OBY^NO OBOZNA^A@T Ox. tO^KA O DELIT KOORDINATNU@ OSX NA DWE ^ASTI: POLOVITELXNU@ POLUOSX, GDE LEVIT TO^- KA e, I OTRICATELXNU@ POLUOSX. kOORDINATOJ TO^KI M NA OSI Ox NAZYWA@T DLINU OTREZKA OM, WZQTU@ SO ZNAKOM +, ESLI TO^KA M LEVIT NA POLOVITELXNOJ POLUOSI, I SO ZNAKOM −, ESLI TO^KA M LEVIT NA OTRICATELXNOJ POLUOSI.

rIS. 3

kAVDOJ TO^KE M NA OSI Ox SOOTWETSTWUET DEJSTWITELXNOE ^ISLO x, A IMENNO, EE KOORDINATA. i OBRATNO, KAVDOMU DEJSTWITELXNOMU ^ISLU NA OSI Ox SOOTWET- STWUET TO^KA, DLQ KOTOROJ \TO DEJSTWITELXNOE ^ISLO QWLQETSQ EE KOORDINATOJ .

9

wSQKIJ RAZ, KOGDA \TO POTREBUETSQ, BUDEM S^ITATX, ^TO MEVDU DEJSTWITELXNY- MI ^ISLAMI I TO^KAMI NEKOTOROJ PRQMOJ USTANOWLENO TAKOGO RODA SOOTWETSTWIE . tAKIM OBRAZOM, SOWOKUPNOSTX WSEH DEJSTWITELXNYH ^ISEL MOVNO RASSMATRIWATX KAK ^ISLOWU@ PRQMU@. iNOGDA WMESTO ^ISLOWOJ PRQMOJ ISPOLXZU@T TAKVE TER - MIN ”WE]ESTWENNAQ PRQMAQ”. oTOVDESTWLENIE DEJSTWITELXNYH ^ISEL S TO^KAMI NA ^ISLOWOJ PRQMOJ BUDET W DALXNEJ[EM POLEZNYM , TAK KAK SLUVIT WSPOMOGATELX- NYM SREDSTWOM DLQ PONIMANIQ I MOTIWIROWKI WWEDENIQ NOWYH PONQTIJ . ~ISLOWU@ PRQMU@, KAK I MNOVESTWO DEJSTWITELXNYH ^ISEL, OBOZNA^A@T ^EREZ R.

sWOJSTWA WE]ESTWENNYH ^ISEL (SM. [z, STR. 33–41]).

aKSIOMA POLNOTY. eSLI A I B — TAKIE NEPUSTYE PODMNOVESTWA R, ^TO DLQ L@BYH \LEMENTOW x A I y B WYPOLNENO x 6 y, TO SU]ESTWUET TAKOE c R, ^TO x 6 c 6 y DLQ L@BYH \LEMENTOW x A I y B.

aBSOL@TNYM ZNA^ENIEM (ILI MODULEM) |a| L@BOGO DEJSTWITELXNOGO ^ISLA a NAZYWA@T DEJSTWITELXNOE ^ISLO, UDOWLETWORQ@]EE USLOWIQM

oTS@DA SLEDUET, ^TO ABSOL@TNOE ZNA^ENIE L@BOGO DEJSTWITELXNOGO ^ISLA NEOTRI - CATELXNO (|a| > 0), A TAKVE

|a| = |−a|, −|a| 6 a 6 |a|, |a| > −a.

gEOMETRI^ESKI |a| SOOTWETSTWUET RASSTOQNI@ MEVDU TO^KAMI ^ISLOWOJ PRQMOJ , IZOBRAVA@]IMI ^ISLA 0 I a.

rASSTOQNIE MEVDU TO^KAMI a I b RAWNO |a − b|. nERAWENSTWO TREUGOLXNIKA: a, b R |a + b| 6 |a| + |b|.

~ISLOWYE MNOVESTWA — MNOVESTWA TO^EK NA PRQMOJ. pODMNOVESTWO h MNO- VESTWA DEJSTWITELXNYH ^ISEL NAZYWA@T PROMEVUTKOM, ESLI WMESTE S L@BYMI

DWUMQ ^ISLAMI x1, x2 \TO PODMNOVESTWO SODERVIT L@BOE x, ZAKL@^ENNOE MEVDU NIMI. iSPOLXZU@T PROMEVUTKI SLEDU@]IH WIDOW (a, b R, a < b):

(a, b) = {x: a < x < b} — OTKRYTYJ PROMEVUTOK, ILI INTERWAL; [a, b] = {x: a < x < b} — ZAMKNUTYJ PROMEVUTOK, ILI OTREZOK;

(a, b] = {x: a < x 6 b} I [a, b) = {x: a 6 x < b} — POLUINTERWALY;

(a, +∞) = {x: x > a}, (−∞, b) = {x: x < b} I (−∞, +∞) = R — BESKONE^NYE

INTERWALY;

[a, +∞) = {x: x > b}, (−∞, b] = {x: x 6 b} — BESKONE^NYE POLUINTERWA-

LY

oTKRYTOE MNOVESTWO — L@BOE OB_EDINENIE INTERWALOW (KONE^NYH ILI BES- KONE^NYH).

mNOVESTWO ZAMKNUTOE, ESLI EGO DOPOLNENIE (W R) OTKRYTOE.

oKRESTNOSTX TO^KI a R — L@BOE OTKRYTOE MNOVESTWO, SODERVA]EE a. oBOZNA^ENIE: U(a).

wYKOLOTAQ (PROKOLOTAQ) OKRESTNOSTX TO^KI a R — TAKOE MNOVESTWO

U˙ (a), ^TO a 6 U˙ (a), A U˙ (a) {a} ESTX OKRESTNOSTX TO^KI a.

mNOVESTWO {x R: |x − a| < ε} = (a − ε, a + ε) NAZYWA@T ε–OKRESTNOSTX@ TO^KI a I OBOZNA^A@T Uε(a), A MNOVESTWO

U˙ ε(a) = Uε(a) \ {a} = (a − ε, a) (a, a + ε) = {x R: 0 < |x − a| < ε}

10