MAiu9

tEOREMA 1 (KRITERIJ kO[I). dLQ SHODIMOSTI POSLEDOWATELXNOSTI NEOBHO - DIMO I DOSTATO^NO, ^TOBY ONA BYLA FUNDAMENTALXNOJ.

dOK–WO. nEOBHODIMOSTX. pO OPREDELENI@, DLQ SHODQ]EJSQ K PREDELU b R POSLEDOWATELXNOSTI IMEEM

tOGDA S U^ETOM NERAWENSTWA TREUGOLXNIKA m > N POLU^IM

ε ε

|xn − xm| = |(xn − b) − (xm − b)| 6 |xn − b| + |xm − b| < 2 + 2 = ε,

^TO SOOTWETSTWUET OPREDELENI@ FUNDAMENTALXNOJ POSLEDOWATELXNOSTI . dOSTATO^NOSTX. pUSTX POSLEDOWATELXNOSTX {xn} FUNDAMENTALXNAQ. sOGLAS-

NO OPREDELENI@ PO PROIZWOLXNOMU ε > 0 MOVNO NAJTI NOMER N(ε), TAKOJ, ^TO IZ

pOSKOLXKU RASSMATRIWAEMAQ POSLEDOWATELXNOSTX IMEET KONE^NOE ^ISLO \LEMEN - TOW S NOMERAMI, NE PREWOSHODQ]IMI N, IZ (1) SLEDUET, ^TO FUNDAMENTALXNAQ PO- SLEDOWATELXNOSTX OGRANI^ENA. dLQ MNOVESTWA ZNA^ENIJ OGRANI^ENNOJ POSLEDOWA - TELXNOSTI SU]ESTWU@T TO^NYE NIVNQQ I WERHNQQ GRANI . dLQ MNOVESTWA ZNA^ENIJ

STWENNO. s UWELI^ENIEM s TO^NAQ NIVNQQ GRANX NE UMENX[AETSQ, A TO^NAQ WERHNQQ GRANX NE UWELI^IWAETSQ, T.E.

as 6 as+1 6 bs+1 6 bs,

I POLU^AEM SISTEMU WLOVENNYH OTREZKOW

[aN , bN ] [aN+1, bN+1] . . . [aN+k, bN+k] . . . , k N.

pO TEOREME O WLOVENNYH OTREZKOW SU]ESTWUET OB]AQ TO^KA , KOTORAQ PRINAD- LEVIT WSEM OTREZKAM. oBOZNA^IM EE ^EREZ b. tAKIM OBRAZOM, k N aN+k 6 b 6 bN+k, A PRI n > N + k IZ OPREDELENIQ as, bs POLU^AEM, ^TO aN+k 6 xn 6 bN+k. oTS@DA PRI n > N + k

tEPERX IZ (1) I OPREDELENIQ as, bs SLEDUET

iZ SRAWNENIQ (2) I (3) W ITOGE POLU^IM

ε > 0 N = N(ε) N : (n > N |b − xn| < ε),

^TO SOOTWETSTWUET OPREDELENI@ PREDELA POSLEDOWATELXNOSTI , T.E.

lim{xn} I lim{xn} = b R. .

pRIMER 1. pOSLEDOWATELXNOSTX {(−1)n} NE QWLQETSQ FUNDAMENTALXNOJ, PO\TO- MU NE IMEET PREDELA.

21

7.2mONOTONNYE POSLEDOWATELXNOSTI

eSLI DLQ POSLEDOWATELXNOSTI {xn} SPRAWEDLIWO NERAWENSTWO xn 6 xn+1 (W ^ASTNO- STI, xn < xn+1) ILI xn > xn+1 (W ^ASTNOSTI, xn > xn+1) n N, TO EE NAZYWA@T

NEUBYWA@]EJ (W ^ASTNOSTI, WOZRASTA@]EJ) ILI NEWOZRASTA@]EJ (W ^ASTNO-

STI, UBYWA@]EJ). |TI NAZWANIQ OB_EDINQ@T OB]IM TERMINOM MONOTONNAQ (W ^ASTNOSTI, STROGO MONOTONNAQ) POSLEDOWATELXNOSTX.

tEOREMA 2 (PRIZNAK wEJER[TRASSA). dLQ SHODIMOSTI MONOTONNOJ POSLEDO- WATELXNOSTI NEOBHODIMO I DOSTATO^NO EE OGRANI^ENNOSTI .

dOK–WO. nEOBHODIMOSTX SLEDUET IZ TEOREMY OB OGRANI^ENNOSTI SHODQ]EJSQ POSLEDOWATELXNOSTI. dOKAVEM DOSTATO^NOSTX.

pREDPOLOVIM, ^TO POSLEDOWATELXNOSTX {xn} NEUBYWA@]AQ, A MNOVESTWO EE ZNA- ^ENIJ OGRANI^ENO SWERHU. tOGDA PO TEOREME O TO^NOJ GRANI MNOVESTWO POSLEDOWA -

TELXNOSTI IMEET TO^NU@ WERHN@@ GRANX, KOTORU@ OBOZNA^IM sup{xn} = b R. w SILU SWOJSTW TO^NOJ WERHNEJ GRANI

sOGLASNO OPREDELENI@ DLQ NEUBYWA@]EJ POSLEDOWATELXNOSTI IMEEM n > N xn > xN . iZ (4) I OPREDELENIQ TO^NOJ WERHNEJ GRANI POLU^AEM

b − ε < xN 6 xn 6 b.

tOGDA |b − xn| = b − xn < ε n > N, A S U^ETOM (4) POLU^IM

ε > 0 N = N(ε) N : (n > N |b − xn| < ε),

^TO SOOTWETSTWUET OPREDELENI@ PREDELA POSLEDOWATELXNOSTI , T.E. lim{xn} I lim{xn} =

b R.

eSLI POSLEDOWATELXNOSTX {xn} NEWOZRASTA@]AQ, TO HOD DOKAZATELXSTWA ANALO- GI^EN. .

TAK KAK EE \LEMENTY POLOVITELXNY. w SILU PRIZNAKA wEJER[TRASSA POSLEDOWA-

TELXNOSTX yn SHODITSQ.

nO TOGDA IZ ARIFMETI^ESKIH SWOJSTW PREDELOW POSLEDOWATELXNOSTEJ POLU^AEM

22

t.E. POSLEDOWATELXNOSTX xn TAKVE SHODITSQ I IMEET TOT VE PREDEL. .

pREDEL RASSMOTRENNOJ POSLEDOWATELXNOSTI, SLEDUQ |JLERU, TRADICIONNO OBO- ZNA^A@T LATINSKOJ BUKWOJ e:

lim 1 + n1 n = e.

8pREDELXNYE TO^KI POSLEDOWATELXNOSTI

sM. [z, STR. 88–89], [as~, STR. 52], [k, STR. 87].

8.1~ASTI^NYJ PREDEL POSLEDOWATELXNOSTI

pUSTX ZADANA POSLEDOWATELXNOSTX {xn} I PUSTX ^ISLA k1 < k2 < . . . < kn < . . .

OBRAZU@T WOZRASTA@]U@ POSLEDOWATELXNOSTX CELYH POLOVITELXNYH ^ISEL . tO-

GDA POSLEDOWATELXNOSTX {yn}, GDE yn = xkn , NAZYWA@T PODPOSLEDOWATELXNOSTX@ ISHODNOJ POSLEDOWATELXNOSTI. o^EWIDNO, ^TO ESLI {xn} IMEET PREDELOM ^ISLO b,

TO L@BAQ EE PODPOSLEDOWATELXNOSTX IMEET TOT VE SAMYJ PREDEL , POSKOLXKU NA^I- NAQ S NEKOTOROGO NOMERA WSE \LEMENTY KAK ISHODNOJ POSLEDOWATELXNOSTI , TAK I L@BOJ EE PODPOSLEDOWATELXNOSTI POPADA@T W L@BU@ WYBRANNU@ OKRESTNOSTX TO^ - KI b. w TO VE WREMQ RASHODQ]AQSQ POSLEDOWATELXNOSTX MOVET IMETX SHODQ]IESQ PODPOSLEDOWATELXNOSTI, PRI^EM K RAZNYM PREDELAM.

pRIMERY. 1) pOSLEDOWATELXNOSTX {(−1)n} IMEET ^ASTI^NYE PREDELY −1, 1. 2) u POSLEDOWATELXNOSTI {n} ^ASTI^NYH PREDELOW NET, TAK KAK L@BAQ EE POD-

POSLEDOWATELXNOSTX NEOGRANI^ENA, A ZNA^IT RASHODITSQ.

uSLOWIE, PRI KOTOROM IZ POSLEDOWATELXNOSTI MOVNO WYDELITX SHODQ]U@SQ POD - POSLEDOWATELXNOSTX, USTANAWLIWAET SLEDU@]AQ TEOREMA.

tEOREMA 1 (bOLXCANO — wEJER[TRASSA) wSQKAQ OGRANI^ENNAQ POSLEDOWA-

TELXNOSTX SODERVIT SHODQ]U@SQ PODPOSLEDOWATELXNOSTX .

dOK–WO. pUSTX WSE \LEMENTY POSLEDOWATELXNOSTI {xn} ZAKL@^ENY MEVDU ^I- SLAMI a I b, T.E. xn [a, b] n N. rAZDELIM OTREZOK [a, b] POPOLAM. tOGDA HOTQ BY ODNA IZ EGO POLOWIN BUDET SODERVATX BESKONE^NOE MNOVESTWO \LEMENTOW POSLEDOWA -

TELXNOSTI, TAK KAK W PROTIWNOM SLU^AE I WESX OTREZOK [a, b] SODERVAL BY KONE^NOE

IH ^ISLO, ^TO NEWOZMOVNO. pUSTX [a1, b1] BUDET TA IZ POLOWIN OTREZKA [a, b], KO- TORAQ SODERVIT BESKONE^NOE MNOVESTWO \LEMENTOW POSLEDOWATELXNOSTI {xn} (ILI ESLI OBE POLOWINY TAKOWY, TO L@BAQ IZ NIH).

aNALOGI^NO IZ OTREZKA [a1, b1] WYDELIM EGO POLOWINU [a2, b2], SODERVA]U@ BESKO-

NE^NOE MNOVESTWO \LEMENTOW POSLEDOWATELXNOSTI , I T.D. pRODOLVAQ \TOT PROCESS, POSTROIM SISTEMU WLOVENNYH OTREZKOW

[a, b] [a1, b1] [a2, b2] . . . [an, bn] . . . ,

PRI^EM bn − an = (b − a)/2n. pO TEOREME O WLOVENNYH OTREZKOW SU]ESTWUET TO^KA x, PRINADLEVA]AQ WSEM \TIM OTREZKAM. pOSTROIM PODPOSLEDOWATELXNOSTX, SHODQ-

]U@SQ K x. dLQ KAVDOGO NATURALXNOGO n IZ [an, bn] WYBEREM \LEMENT xkn POSLEDO- WATELXNOSTI. |TO WOZMOVNO, TAK KAK KAVDYJ TAKOJ OTREZOK SODERVIT BESKONE^NOE

MNOVESTWO \LEMENTOW POSLEDOWATELXNOSTI .

23

W [aN , bN ], TO xkn [an, bn] [aN , bN ] Uε(x) DLQ WSEH n > N. .

mETOD RASSUVDENIJ, ISPOLXZOWANNYJ PRI DOKAZATELXSTWE \TOJ TEOREMY I SWQ - ZANNYJ S POSLEDOWATELXNYM DELENIEM POPOLAM RASSMATRIWAEMYH OTREZKOW , IZWE- STEN POD NAZWANIEM METODA bOLXCANO. |TOT METOD ISPOLXZUETSQ PRI DOKAZATELX- STWO MNOGIH SLOVNYH TEOREM.

~ASTI^NYM PREDELOM ILI PREDELXNOJ TO^KOJ POSLEDOWATELXNOSTI NAZY-

WA@T PREDEL KAKOJ–LIBO EE PODPOSLEDOWATELXNOSTI.

zAME^ANIE. rAZLI^IE PONQTIJ PREDELA I ^ASTI^NOGO PREDELA W TOM , ^TO W SLU^AE PREDELA WNE EGO OKRESTNOSTI NAHODITSQ KONE^NOE ^ISLO \LEMENTOW POSLEDO - WATELXNOSTI I BESKONE^NOE WNUTRI, A W SLU^AE ^ASTI^NOGO PREDELA — BESKONE^NOE ^ISLO WNUTRI I, MOVET BYTX, BESKONE^NOE WNE.

8.2wERHNIJ I NIVNIJ PREDELY POSLEDOWATELXNOSTI

nAIBOLX[IJ (NAIMENX[IJ) ^ASTI^NYJ PREDEL POSLEDOWATELXNOSTI {xn} NAZYWA@T

WERHNIM (NIVNIM) PREDELOM POSLEDOWATELXNOSTI I OBOZNA^A@T: lim xn I

lim xn.

tEOREMA O SU]ESTWOWANII WERHNEGO I NIVNEGO PREDELA POSLEDOWA-

TELXNOSTI. u L@BOJ OGRANI^ENNOJ POSLEDOWATELXNOSTI SU]ESTWUET KAK NAIBOLX - [IJ, TAK I NAIMENX[IJ ^ASTI^NYJ PREDEL.

dOK–WO. dOKAVEM SU]ESTWOWANIE NAIBOLX[EGO ^ASTI^NOGO PREDELA . pUSTX {xn} — OGRANI^ENNAQ POSLEDOWATELXNOSTX. iZ TEOREMY bOLXCANO — wEJER[TRASSA SLEDUET, ^TO MNOVESTWO A ^ASTI^NYH PREDELOW \TOJ POSLEDOWATELXNOSTI NE PUSTO . iZ OGRANI^ENNOSTI POSLEDOWATELXNOSTI SLEDUET I OGRANI^ENNOSTX MNOVESTWA A. w SILU \TOGO MNOVESTWO A IMEET KONE^NU@ WERHN@@ GRANX. pOKAVEM, ^TO b = sup A QWLQETSQ ^ASTI^NYM PREDELOM, T.E. ^TO b A. dEJSTWITELXNO, ESLI b 6 A, TO PO OPREDELENI@ ^ASTI^NOGO PREDELA SU]ESTWUET TAKOE ε > 0, ^TO W INTERWALE (b − ε, b + ε) SODERVITSQ LI[X KONE^NOE ^ISLO ^LENOW POSLEDOWATELXNOSTI {xn}, I PO\TOMU W \TOM INTERWALE NET NI ODNOGO ^ASTI^NOGO PREDELA , T.E. \LEMENTA A. a \TO PROTIWORE^IT USLOWI@ b = sup A. tAKIM OBRAZOM, b A I, SLEDOWATELXNO, b QWLQETSQ NAIBOLX[IM \LEMENTOM MNOVESTWA A, PO\TOMU b = limxn.

aNALOGI^NO DOKAZYWAETSQ SU]ESTWOWANIE NAIMENX[EGO ^ASTI^NOGO PREDELA . .

eSLI POSLEDOWATELXNOSTX {xn} NEOGRANI^ENA I NE IMEET NAIBOLX[EGO (NAIMENX- [EGO) ^ASTI^NOGO PREDELA, TO POLAGA@T lim xn = +∞ (lim xn = −∞).

9tOPOLOGI^ESKIE SWOJSTWA ^ISLOWYH MNOVESTW

9.1pREDELXNYE TO^KI MNOVESTW

sM. [z, STR. 69–70].

24

tO^KU x R NAZYWA@T PREDELXNOJ TO^KOJ MNOVESTWA E R, ESLI L@BAQ OKRESTNOSTX TO^KI x SODERVIT HOTQ BY ODNU TO^KU MNOVESTWA E, OTLI^NU@ OT x.

tEOREMA 1 (TEOREMA O PREDELXNOJ TO^KE). wSQKOE OGRANI^ENNOE BESKONE^-

NOE PODMNOVESTWO PRQMOJ R IMEET PREDELXNU@ TO^KU W R.

dLQ DOK–WA ISPOLXZUEM METOD bOLXCANO. pUSTX E — OGRANI^ENNOE BESKONE^NOE

^ISLOWOE MNOVESTWO. tOGDA E LEVIT WNUTRI NEKOTOROGO OTREZKA I0. dELIM OTREZOK POPOLAM: I0 I1 I2 . . . , WYBIRAQ KAVDYJ RAZ TU POLOWINU In OTREZKA In−1, KOTORAQ SODERVIT BESKONE^NOE ^ISLO \LEMENTOW E, T.E. En = E In — BESKONE^NOE MNOVESTWO DLQ L@BOGO n = 1, 2, . . ..

SU]ESTWUET TAKOE n, ^TO |In| < ε, A ZNA^IT, In Uε(x) = (x − ε, x + ε), POSKOLXKU x In. tAK KAK En = E In — BESKONE^NOE MNOVESTWO I En Uε(x), TO OKRESTNOSTX E, OTLI^NU@ OT x. t.E. x — PREDELXNAQ TO^KA

9.2wNUTRENNOSTX I ZAMYKANIE MNOVESTWA

zADA^A 1. dOKAVITE, ^TO

1)OB_EDINENIE L@BOGO (KONE^NOGO ILI BESKONE^NOGO) SEMEJSTWA OTKRYTYH MNO- VESTW ESTX OTKRYTOE MNOVESTWO;

2)PERESE^ENIE L@BOGO KONE^NOGO SEMEJSTWA OTKRYTYH MNOVESTW ESTX OTKRYTOE MNOVESTWO.

zADA^A 2. pRIWEDITE PRIMER BESKONE^NOGO SEMEJSTWA OTKRYTYH MNOVESTW , PERESE^ENIE KOTOROGO NE QWLQETSQ OTKRYTYM MNOVESTWOM .

tEOREMA 2. 1. mNOVESTWO E R OTKRYTO T. I T. T., K. L@BAQ TO^KA MNOVESTWA E ESTX WNUTRENNQQ TO^KA MNOVESTWA E, T.E. Int E = E.

2. mNOVESTWO E R ZAMKNUTO T. I T. T., K. L@BAQ PREDELXNAQ TO^KA MNOVESTWA E ESTX TO^KA MNOVESTWA E, T.E. [E] = E.

zADA^A 3. dOKAVITE \TU TEOREMU.

9.3oTKRYTYE POKRYTIQ MNOVESTW

sM. [z, STR. 69].

oTKRYTYM POKRYTIEM MNOVESTWA E R NAZYWA@T TAKOE SEMEJSTWO {Gα}α I

OTKRYTYH PODMNOVESTW Gα R, ^TO E α I Gα.

oTKRYTOE POKRYTIE {Gα}α I1 MNOVESTWA E R NAZYWA@T PODPOKRYTIEM POKRYTIQ {Gα}α I , ESLI I1 I.

25

mNOVESTWO E R NAZYWA@T KOMPAKTNYM (KOMPAKTOM), ESLI IZ L@BOGO EGO OTKRYTOGO POKRYTIQ MOVNO WYDELITX KONE^NOE PODPOKRYTIE .

tEOREMA 3 (TEOREMA O KONE^NOM POKRYTII). mNOVESTWO E R KOMPAKTNO T. I T. T., K. ONO ZAMKNUTO I OGRANI^ENO.

dOK–WO METODOM bOLXCANO:

(”OT PROTIWNOGO”) PUSTX SU]ESTWUET OTKRYTOE POKRYTIE {Gα} MNOVESTWA E, NE SODERVA]EE KONE^NOGO PODPOKRYTIQ. tAK KAK E OGRANI^ENO, TO SU]ESTWUET TAKOJ OTREZOK I0, ^TO E I0. dELIM OTREZOK POPOLAM: I0 I1 I2 . . . , WYBIRAQ KAVDYJ RAZ TU POLOWINU In OTREZKA In−1, DLQ KOTOROJ MNOVESTWO En = E In NE POKRYWAETSQ NIKAKIM KONE^NYM PODPOKRYTIEM {Gα}. iZ \TOGO USLOWIQ SLEDUET BESKONE^NOSTX En. rASSUVDAQ ANALOGI^NO DOKAZATELXSTWU TEOREMY O PREDELXNOJ TO^KE, DOKAZYWAEM, ^TO SU]ESTWUET TO^KA x ∩nIn, KOTORAQ QWLQETSQ PREDELXNOJ DLQ MNOVESTWA E.

tAK KAK MNOVESTWO E ZAMKNUTO, TO PO TEOREME 2 (^ASTX 2) L@BAQ EGO PREDELXNAQ

TO^KA ESTX TO^KA E. pO\TOMU x E, A ZNA^IT, x Gα0 DLQ NEKOTOROGO α0. mNO- VESTWO Gα0 OTKRYTO, x Gα0 ∩ In, A DLINA OTREZKA In STREMITSQ K 0 PRI n → ∞. pO\TOMU NAJDETSQ TAKOE n, ^TO In Gα0 , NO \TO PROTIWORE^IT WYBORU In, TAK KAK MNOVESTWO En = E In NE POKRYWAETSQ NIKAKIM KONE^NYM PODPOKRYTIEM {Gα}. dOK–WO , OGRANI^ENOSTX. rASSMOTRIM OTKRYTOE POKRYTIE MNOVESTWA E

INTERWALAMI Un(0), n N (n–OKRESTNOSTI 0). tAK KAK E KOMPAKTNO, TO SU]ESTWUET

EGO KONE^NOE PODPOKRYTIE Uni (0), i = 1, . . . , k. iMEEM Un1 (0) · · · Unk (0) PRI n1 < · · · < nk. a ZNA^IT, E Unk (0), I E OGRANI^ENO.

dOK–WO , ZAMKNUTOSTX. dOSTATO^NO DOKAZATX OTKRYTOSTX E. dLQ \TOGO

RASSMOTRIM PROIZWOLXNU@ TO^KU z E I DLQ KAVDOJ TO^KI x E NEPERESEKA@- ]IESQ OKRESTNOSTI Uδx (x) I Uδx (z) TO^EK x I z SOOTWETSTWENNO, GDE δx = |x − z|/3.

nn

[[

WNUTRENNQQ TO^KA E. pOSKOLXKU z — PROIZWOLXNAQ TO^KA E, TO PO TEOREME 2 (^ASTX 1) E OTKRYTO, A ZNA^IT, E ZAMKNUTO. .

26

10 pREDEL FUNKCII

10.1wIDY PREDELOW

sM. [z, STR. 105–107].

wSPOMNIM OPREDELENIE PREDELA POSLEDOWATELXNOSTI :

b = lim zn ε > 0 N = N(ε) N : (n > N |zn − b| < ε).

eSLI W \TOM OPREDELENII ZAMENITX POSLEDOWATELXNOSTX {zn} NA FUNKCI@ f(x), A NATURALXNYE ^ISLA n I N — NA DEJSTWITELXNYE x I M, TO POLU^IM OPREDELENIE

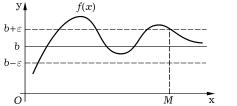
PREDELA FUNKCII f(x) PRI STREMLENII ARGUMENTA K +∞:

rIS. 7

iZ RIS. 7 QSNO, KAK PO ZADANNOMU ZNA^ENI@ ε WYBRATX POLOVENIE TO^KI M, PRI KOTOROM BUDET WYPOLNENO USLOWIE \TOGO OPREDELENIQ . gRAFIK FUNKCII PRI x → +∞ NEOGRANI^ENNO PRIBLIVAETSQ K GORIZONTALXNOJ PRQMOJ y = b, NAZYWAEMOJ W \TOM SLU^AE PRAWOSTORONNEJ GORIZONTALXNOJ ASIMPTOTOJ GRAFIKA FUNKCII.

zADA^A 1. dOKAVITE, ^TO USLOWIE (1) \KWIWALENTNO USLOWI@

oPREDELENIE (1) MOVET BYTX OBOB]ENO NA SLU^AJ x → a SLEDU@]IM OBRAZOM. iNTERPRETIRUEM MNOVESTWO TEH x, KOTORYE UDOWLETWORQ@T NERAWENSTWU x > M, KAK OKRESTNOSTX (WYKOLOTU@ OKRESTNOSTX) SIMWOLA +∞:

UM (+∞) = U˙ M (+∞) = {x R: x > M} = (M, +∞).

i PEREPI[EM USLOWIE (1) W WIDE:

→

nAKONEC, PEREPISYWAQ USLOWIQ PRINADLEVNOSTI OKRESTNOSTQM W WIDE NERAWENSTW , POLU^AEM OPREDELENIE PREDELA FUNKCII f(x) PRI STREMLENII ARGUMENTA K TO^KE:

27

T.E. TO^KU b R NAZYWA@T PREDELOM FUNKCII f(x) W TO^KE a R (ILI PRI x,

STREMQ]EMSQ K a R), ESLI, KAKOWO BY NI BYLO POLOVITELXNOE ^ISLO ε, NAJDETSQ TAKOE POLOVITELXNOE ^ISLO δ, ^TO DLQ WSEH TO^EK WYKOLOTOJ δ–OKRESTNOSTI TO^KI a ZNA^ENIQ FUNKCII PRINADLEVAT ε–OKRESTNOSTI TO^KI b.

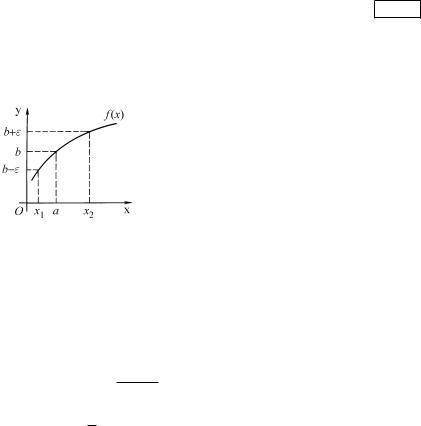
zAPISX δ(ε) W (3) POD^ERKIWAET, ^TO ZNA^ENIE δ ZAWISIT OT WYBORA ε. rIS. 8 rIS.8 ILL@STRIRUET, ^TO DLQ NAHOVDENIQ δ PRI ZADANNOM ε PO GRAFIKU FUNKCII SLEDUET

NAJTI BLIVAJ[IE K a TO^KI x1 I x2, W KOTORYH FUNKCIQ PRINIMAET ZNA^ENIQ b −ε I b + ε SOOTWETSTWENNO, I POLOVITX δ RAWNYM MENX[EMU IZ RASSTOQNIJ OT TO^KI a DO NAJDENNYH TO^EK.

rIS. 8

iZ OPREDELENIQ SLEDUET, ^TO FUNKCIQ f(x) DOLVNA BYTX OPREDELENA W NEKOTOROJ WYKOLOTOJ OKRESTNOSTI TO^KI a, INA^E USLOWIE (2) NE MOVET WYPOLNQTXSQ. pRI \TOM TO^KA a MOVET I NE PRINADLEVATX OBLASTI OPREDELENIQ FUNKCII , A ESLI I PRINADLEVIT, TO ZNA^ENIE f(a) NE U^ITYWA@T.

tO^KA a MOVET NE IMETX WYKOLOTOJ OKRESTNOSTI W OBLASTI Df OPREDELENIQ

√

FUNKCII (NAPRIMER, DLQ FUNKCII f(x) = x TO^KA x = 0 W Df = {x R: x > 0}). tOGDA IZMENENIE ARGUMENTA x PRI x → a IMEET SMYSL LI[X W RASPOLOVENNOJ PO

ODNU STORONU OT TO^KI a WYKOLOTOJ POLUOKRESTNOSTI. nO DAVE W SLU^AE, KOGDA FUNKCIQ OPREDELENA W WYKOLOTOJ OKRESTNOSTI TO^KI a, DLQ ANALIZA OSOBENNOSTEJ POWEDENIQ FUNKCII PRI x → a BYWAET CELESOOBRAZNO OGRANI^ITX ”SWOBODU” IZ- MENENIQ ARGUMENTA x ODNOJ IZ WYKOLOTYH POLUOKRESTNOSTEJ \TOJ TO^KI . tAKOE OGRANI^ENIE PRIWODIT K PONQTI@ ODNOSTORONNEGO PREDELA . kROME TOGO, WOZMOVNY STREMLENIQ x K −∞ ILI ∞. dLQ POLU^ENIQ SOOTWETSTWU@]IH OPREDELENIJ WWEDEM PONQTIQ OKRESTNOSTI (WYKOLOTOJ OKRESTNOSTI) SIMWOLOW a+, a−, −∞ I ∞:

tOGDA USLOWIE (2) IMEET SMYSL I W SLU^AE, KOGDA a ZAMENQETSQ NA a+, a−, +∞, −∞ ILI ∞, A b — NA +∞, −∞ ILI ∞. zAMENQQ W POLU^ENNOJ ZAPISI (2) USLOWIQ PRINAD- LEVNOSTI OKRESTNOSTQM NA NERAWENSTWA, POLU^AEM SOOTWETSTWU@]EE OPREDELENIE PREDELA FUNKCII. nAPRIMER, TAK POLU^AETSQ OPREDELENIE:

28

pREDELY limx→a− f(x) I limx→a+ f(x) NAZYWA@T LEWYM I PRAWYM (ILI ODNO-

STORONNIMI) PREDELAMI FUNKCII f(x) W TO^KE a. ~TOBY OTLI^ITX OT ODNO-

STORONNIH, PREDELY S x → a NAZYWA@T DWUSTORONNIMI.

aNALIZIRUQ WSE POLU^A@]IESQ OPREDELENIQ, ZAMETIM, ^TO PRI x → a, a−, a+ DOSTATO^NO RASSMATRIWATX DLQ δ SKOLX UGODNO MALYE POLOVITELXNYE ZNA^ENIQ , A PRI x → +∞, −∞, ∞ — SKOLX UGODNO BOLX[IE ZNA^ENIQ M. aNALOGI^NO, ESLI PREDEL ESTX ^ISLO b, TO DOSTATO^NO RASSMATRIWATX DLQ ε SKOLX UGODNO MALYE POLO- VITELXNYE ZNA^ENIQ. kOGDA VE FUNKCIQ IMEET KAKOJ–LIBO BESKONE^NYJ PREDEL, DOSTATO^NO RASSMATRIWATX SKOLX UGODNO BOLX[IE ZNA^ENIQ E.

oTMETIM TAKVE, ^TO SIMWOLY a+, a−, +∞, −∞ I ∞ NE QWLQ@TSQ ^ISLAMI, HOTQ DLQ NIH BYLI WWEDENY PONQTIQ OKRESTNOSTI (WYKOLOTOJ OKRESTNOSTI).

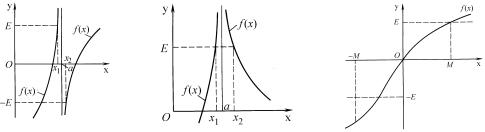
zADA^A 2. kAKIE PREDELY ILL@STRIRU@T RIS. 9–11 ? pRIWEDITE SOOTWETSTWU- @]IE OPREDELENIQ.

10.2bAZA MNOVESTW. pREDEL FUNKCII PO BAZE

sM. [z, STR. 125–128], [as~, SS. 55–59].

mY POKAZALI, ^TO NA WSE RASSMOTRENNYE SLU^AI PREDELA WOZMOVEN WZGLQD S EDI - NOJ TO^KI ZRENIQ: DOSTATO^NO WWESTI PONQTIQ OKRESTNOSTI (WYKOLOTOJ OKRESTNO- STI) SOOTWETSTWU@]IH SIMWOLOW. sEMEJSTWO TAKIH OKRESTNOSTEJ NAZYWA@T BAZOJ . tO^NAQ FORMULIROWKA \TOGO PONQTIQ POZWOLIT KAVDOE SWOJSTWO PREDELOW FORMU - LIROWATX I DOKAZYWATX ODIN RAZ, A NE DLQ KAVDOGO TIPA PREDELOW OTDELXNO.

sEMEJSTWO B = {bα} PODMNOVESTW MNOVESTWA A : bα A, NAZYWA@T BAZOJ W MNOVESTWE A, ESLI:

pUSTX A — OBLASTX OPREDELENIQ FUNKCII, B — BAZA W MNOVESTWE A. ~ISLO d

NAZYWA@T PREDELOM FUNKCII f(x) PO BAZE B, ESLI

pRI \TOM ISPOLXZU@T OBOZNA^ENIE: d = lim f(x). w DANNOM OPREDELENII WOZMOVNO

B

A 6 R (\TOT SLU^AJ MY BUDEM RASSMATRIWATX W SLEDU@]EM SEMESTRE ), NO OBQZA- TELXNO OBLASTX ZNA^ENIJ f ESTX ^ISLOWOE MNOVESTWO.

29

nAIBOLEE UPOTREBITELXNYE BAZY SLEDU@]IE.

–bAZA B0 NA MNOVESTWE N SOSTOIT IZ MNOVESTW Ns = {s, s+1, s+2, . . .}, s N. pREDEL PO \TOJ BAZE ESTX PREDEL POSLEDOWATELXNOSTI .

–bAZA B1 NA MNOVESTWE R SOSTOIT IZ MNOVESTW U˙ δ(a), δ > 0. pREDEL PO \TOJ

eSLI FUNKCIQ NE OPREDELENA NA WSEJ PRQMOJ, TO ONA NE MOVET IMETX PREDELA PO BAZAM B1, . . . B6. pREDELY, OPREDELENNYE W PREDYDU]EM PUNKTE, IME@T SMYSL TOLXKO, ESLI FUNKCIQ OPREDELENA W NEKOTOROJ WYKOLOTOJ OKRESTNOSTI SOOTWETSTWU - @]EGO SIMWOLA. dLQ POLU^ENIQ BOLEE OB]EGO OPREDELENIQ PERENESEM RASSMOTREN -

zADA^A 3. pOKAVITE, ^TO B0, B1, . . . B6, B1A, . . . B6A ESTX BAZY W SOOTWETSWU@]IH MNOVESTWAH, A PREDELY PO BAZAM B1A, . . . B6A SOWPADA@T S SOOTWETSTWU@]IMI PREDE-

LAMI, OPREDELENNYMI W PREDYDU]EM PUNKTE, ESLI OBLASTX A OPREDELENIQ FUNKCII SODERVIT NEKOTORU@ WYKOLOTU@ OKRESTNOSTX SOOTWETSTWU@]EGO SIMWOLA .

pRIMER 3. pOKAVEM, ^TO lim c = c. dEJSTWITELXNO, PRI L@BOM x |f(x) − c| =

B

|c − c| = 0 < ε, ESLI ε — PROIZWOLXNOE POLOVITELXNOE ^ISLO. pO\TOMU W KA^ESTWE b MOVNO WZQTX L@BOJ \LEMENT BAZY B.

30