
MAiu9
.pdftO^KA RAZRYWA a R FUNKCII f : E → R NAZYWAETSQ TO^KOJ USTRANIMOGO RAZRYWA, ESLI SU]ESTWUET NEPRERYWNAQ FUNKCIQ f¯: E {a} → R TAKAQ, ^TO
f |
E\{a} |
= f¯ E\{a}. |
|
|
|
oTMETIM, ^TO IMEETSQ ^ETYRE WARIANTA SU]ESTWOWANIQ I NESU]ESTWOWANIQ PREDELOW f(a − 0) I f(a + 0):
1)a — NE PREDELXNAQ TO^KA MNOVESTWA E∩(−∞; a) ILI SOOTWETSTWENNO E∩(a; +∞); a — PREDELXNAQ TO^KA, PRI \TOM
2)PREDEL NE SU]ESTWUET,
3)PREDEL BESKONE^EN ILI
4)PREDEL KONE^EN.
tO^KU RAZRYWA a R FUNKCII f : E → R NAZYWA@T TO^KOJ RAZRYWA 1–GO RODA, ESLI PREDELY f(a − 0) I f(a + 0) SU]ESTWU@T I KONE^NY. oSTALXNYE TO^KI RAZRYWA NAZYWA@T TO^KAMI RAZRYWA 2–GO RODA. tAKIM OBRAZOM, TO^KA RAZRYWA a R FUNKCII f : E → R ESTX TO^KA RAZRYWA 2–GO RODA, ESLI PREDEL f(a − 0) ILI PREDEL f(a + 0), ILI ONI OBA NE SU]ESTWU@T ILI BESKONE^NY.
iZ OPREDELENIJ SLEDUET, ^TO TO^KA USTRANIMOGO RAZRYWA ESTX TO^KA RAZRYWA 1–GO RODA.
tO^KU RAZRYWA 2–GO RODA a R FUNKCII f : E → R NAZYWA@T TO^KOJ BESKO- NE^NOGO RAZRYWA, ESLI ODIN IZ PREDELOW f(a − 0), f(a + 0) BESKONE^EN, A WTOROJ KONE^EN ILI BESKONE^EN.
pRIMERY. |
|
|
|
|
|
4. |
fUNKCIQ sin 1 |
|
0 NEBESKONE^NYJ RAZRYW 2–GO RODA. |
||
5. |
x IMEET W TO^KE |
|
|
|
|
fUNKCIQ |
|
0 |
PRI |
x R \ Q, |
|
|
D |
||||
|
|
(x) = |
1 |
PRI |
x Q, |
KOTORAQ NAZYWAETSQ FUNKCIEJ dIRIHLE, RAZRYWNA WO WSEH TO^KAH, PRI^EM WSE ONI TO^KI NEBESKONE^NOGO RAZRYWA 2–GO RODA. dEJSTWITELXNO, NA L@BOM INTERWALE ESTX KAK RACIONALXNYE, TAK I IRRACIONALXNYE ^ISLA. pO\TOMU W L@BOJ TO^KE a PREDELY D(a − 0) I D(a + 0) NE SU]ESTWU@T.
6. rASSMOTRIM FUNKCI@ rIMANA
|
|
|
1 |
PRI |
|
m |
|
m |
|
NESOKRATIMAQ DROBX |
|
||
|
R(x) = ( n |
xx = n |
,Q, GDE |
n |
— |
, |
|||||||
|
PRI |
|
|
|
|||||||||
|
|
0 |
|
R \ Q |
|
|
|
|
|
|
|||
zAMETIM |
|
^TO DLQ L@BOGO |
N N |
W L@BOJ OKRESTNOSTI |
a |
PROIZWOLXNOJ TO^KI |
|||||||
|
, |
|
|
|
|
|
|
|
U(m) |
|
|
||
a R IMEETSQ TOLXKO KONE^NOE ^ISLO RACIONALXNYH ^ISEL n , m Z, n N, TAKIH, |
|||||||||||||
^TO n < N. uMENX[IM OKRESTNOSTX U(a) TAK, |
^TOBY W NEJ NE BYLO TAKIH ^ISEL |
||||||||||||
(KROME, BYTX MOVET, SAMOGO ^ISLA a, ESLI a Q). tOGDA |
|
˙ |
|
||||||||||
x U(a) |R(x)| 6 1/N. |
|||||||||||||
tAKIM OBRAZOM, DLQ PROIZWOLXNOGO ε > 0, WYBIRAQ N N TAK, ^TOBY 1/N < ε,
WYBIRAQ SOOTWETSTWU@]U@ OKRESTNOSTI ˙ |
|
˙ |
|
|R(x)| < ε. |
||||||
|
|
|
|
U(a), POLU^AEM, ^TO x |
U(a) |
|||||
a \TO OZNA^AET |
, |
^TO |
lim |
(x) = 0 W PROIZWOLXNOJ TO^KE a |
|
R. |
t |
E |
. |
FUNKCIQ |
|
|
x→a R |
|
. |
|
|
||||
rIMANA NEPRERYWNA W L@BOJ IRRACIONALXNOJ TO^KE I IMEET USTRANIMYJ RAZRYW W L@BOJ RACIONALXNOJ TO^KE.
zADA^A 1. dLQ KAVDOGO IZ 4 TIPOW RAZRYWOW PRIWEDITE PRIMER FUNKCII S TAKIM RAZRYWOM W WIDE RISUNKA EE GRAFIKA.
51
18 tEOREMY O NEPRERYWNOSTI
sM. [z: STR. 159–166].
18.1pONQTIE RAWNOMERNOJ NEPRERYWNOSTI
fUNKCIQ f : E → R RAWNOMERNO NEPRERYWNA, ESLI
ε > 0 δ = δ(ε) > 0 : x1, x2 E |x1 −x2| < δ |f(x1) −f(x2)| < ε . (1)
oTLI^IE \TOGO PONQTIQ OT PONQTIQ NEPRERYWNOSTI NA E ZAKL@^AETSQ W TOM, ^TO δ W (1) NE ZAWISIT NI OT x1, NI OT x2. tOGDA KAK: f NEPRERYWNA NA E
x0 E ε > 0 δ = δ(ε, x0) > 0 : x E |x−x0| < δ |f(x)−f(x0)| < ε .
T.E. δ ZAWISIT OT x0.
tEOREMA 1. fUNKCIQ f : E → R, RAWNOMERNO NEPRERYWNAQ NA E, NEPRERYWNA NA E.
dOK–WO SLEDUET IZ OPREDELENIJ: |
POLAGAQ W USLOWII |
(1) x1 |
= |
x I x2 = x0, |
|||||
POLU^AEM USLOWIE NEPRERYWNOSTI FUNKCII f W TO^KE x0. |
|
|
|
||||||
pRIMERY FUNKCIJ, KOTORYE NEPRERYWNY, NO NE RAWNOMERNO NEPRERYWNY: |
|||||||||
1) |
1 |
NA (0; 1]; |
2) sin |
1 |
NA (0; 1]; |
3) |
sin x2 |
NA |
R. |
x |
|
|
|||||||
|
|
x |
|
|
|
|
|
||
dLQ DOK–WA TOGO, ^TO DLQ DANNYH FUNKCIJ USLOWIE (1) NE WYPOLNQETSQ, ZAPI[EM EGO OTRICANIE:
ε > 0 δ = δ(ε) > 0 x1, x2 E : |x1 − x2| < δ, |f(x1) − f(x2)| > ε. (2)
dLQ KAVDOJ IZ TREH FUNKCIJ f NAJDEM DWE TAKIE POSLEDOWATELXNOSTI {xn} I {zn}
IZ SOOTWETSTWU@]EGO MNOVESTWA E, ^TO |f(xn) − f(zn)| > 1 I |
nlim |xn − zn| = 0. |
|
→∞ |
tOGDA USLOWIE (2) BUDET WYPOLNQTXSQ PRI ε = 1, A ZNA^IT, UKAZANNYE FUNKCII NE RAWNOMERNO NEPRERYWNY NA E.
w KA^ESTWE POSLEDOWATELXNOSTEJ {xn} I {zn} DLQ FUNKCIJ 1)—3) MOVNO WY- BRATX:
1 |
1 |
|
|
1 |
|
|
1 |
|
|||||||
1) xn = |
|
, zn = |
|
; 2) |
xn = |
|
|
|
, zn = |
|
|
|
|
; |
|
n |
n + 1 |
π/2 + 2πn |
−π/2 + 2πn |
||||||||||||
|
|
|
|
3) |
xn = r |
|
|
, zn = r |
|
|
. . |
|
|||
|
|
|
|
|
2 (n + 1) |
|
2 n |
|
|||||||
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
tEOREMA 2 (kANTORA O RAWNOMERNOJ NEPRERYWNOSTI). fUNKCIQ, NEPRERYWNAQ NA KOMPAKTE, RAWNOMERNO NEPRERYWNA NA NEM.
dOK–WO. pUSTX K R — KOMPAKT, f : K → R — NEPRERYWNAQ NA K FUNKCIQ. wYBEREM PROIZWOLXNOE ε > 0. w SILU NEPRERYWNOSTI f NA K
a K δ(a) = δ( |
ε |
, a) > 0 : |
x Uδ(a)(a) ∩ K |f(x) − f(a)| < |
|
ε |
. (3) |
|
|
|
|
|
||||
2 |
2 |
||||||
52
rASSMOTRIM OTKRYTOE POKRYTIE {V (a) = Uδ(a)/2(a) : a K} MNOVESTWA K. |
w |
||||||||||||||||||||||
SILU KOMPAKTNOSTI K IZ \TOGO POKRYTIQ MOVNO WYBRATX KONE^NOE PODPOKRYTIE |
|||||||||||||||||||||||
{V (a1), . . . , V (an)}. pOLOVIM δ = 21 min{δ(a1); . . . ; δ(an)}. |
|
|
|
|
|
|
|
|
|
||||||||||||||
tEPERX WOZXMEM TAKIE TO^KI a0, a00 K, ^TO |a0 |
− a00| < δ . pUSTX i — TAKOJ |
||||||||||||||||||||||
NOMER, ^TO a0 |
V (ai). |
tOGDA |a0 − ai| < δ(ai)/2 < δ(ai) I a0 |
Uδ(ai)(ai). a W SILU |
||||||||||||||||||||
NERAWENSTWA TREUGOLXNIKA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|a00 − ai| 6 |a0 − a00| + |a0 − ai| < δ + |
δ(ai) |
6 |
δ(ai), |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||
I PO\TOMU a00 |
Uδ(ai)(ai). nA OSNOWANII TOGO VE NERAWENSTWA TREUGOLXNIKA I (3) |
||||||||||||||||||||||
IMEEM |
|
f(a00) − f(a0) |
|
6 f(a00) − f(ai) + f(ai) − f(a0) < |
|
ε |
|
ε |
|
|
|
||||||||||||
|
|
|
|
|
+ |
|
|
= ε. |
|
|
|||||||||||||
|
|
|
2 |
2 |
|
|
|||||||||||||||||
iTAK DLQ |
KAVDOJ PARY |
TO^EK |
|
IZ USLOWIQ |
|
|
|
|
|
|
|
|
SLEDUET NE |
|
|||||||||
RAWENSTWO, |
|
|
|
|
|
|
|
|
a0, a00 K |
|
|
|
|a0 − a00| |
< δ |
|
|
- |
||||||
|
|
f(a00) − f(a0) |
|
< ε, PRI^EM ^ISLO δ ZAWISIT LI[X OT WYBORA ε I NE |
|||||||||||||||||||
ZAWISIT OT POLOVENIQ |
\TIH |
TO^EK, ^TO PO OPREDELENI@ SOOTWETSTWUET RAWNOMERNOJ |
|||||||||||||||||||||
NEPRERYWNOSTI |
f NA K. |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
18.2kRITERIJ NEPRERYWNOSTI MONOTONNOJ FUNKCII
tEOREMA 3 (O TO^KAH RAZRYWA MONOTONNOJ FUNKCII). mONOTONNAQ FUNKCIQ MOVET IMETX RAZRYWY TOLXKO 1–GO RODA.
dOK–WO. pUSTX c — TO^KA RAZRYWA NEUBYWA@]EJ FUNKCII f : E → R. pO OPREDELENI@ TO^KI RAZRYWA c — PREDELXNAQ TO^KA I LEWOJ E ∩ (−∞; c), I PRA- WOJ E ∩ (c; +∞) ^ASTI OBLASTI E OPREDELENIQ f. w ^ASTNOSTI, E ∩ (c; +∞) —
OGRANI^EN SWERHU ZNA^ENIEM f(c1), GDE c1 E ∩ (c; +∞). pO |
|
|
NEPUSTOE MNOVESTWO. tAK KAK f — NEUBYWA@]AQ FUNKCIQ, OBRAZ f E ∩ (−∞; c) |
|
|
TEOREME O TO^NOJ
GRANI SU]ESTWUET b = sup f E ∩ (−∞; c) . pO OPREDELENI@ TO^NOJ WERHNEJ GRA-
NI DLQ L@BOGO ε > 0 SU]ESTWUET TAKOE b1 f |
E ∩ (−∞; c) |
, ^TO b1 (b − ε, b]. |
||||
TO^KA |
c1 E |
∩ (−∞; c) |
TAKAQ |
, |
^TO |
|
pO OPREDELENI@ OBRAZA MNOVESTWA SU]ESTWUET |
|
|
|
|||
f(c1) = b1. oBOZNA^IM δ = c − c1. iSPOLXZUQ MONOTONNOSTX f I OPREDELENIQ b1 |
||||||
I b, POLU^AEM b1 = f(c − δ) 6 f(x) 6 b DLQ L@BOGO x E ∩ (c − δ, c], A ZNA^IT, 0 6 b − f(x) 6 b − b1 < ε. pO OPREDELENI@ LEWOGO PREDELA b = f(c − 0).
aNALOGI^NO DOKAZYWAETSQ SU]ESTWOWANIE KONE^NOGO PREDELA f(c + 0) I RASSMATRIWAETSQ SLU^AJ NEWOZRASTA@]EJ FUNKCII. tAKIM OBRAZOM, c — TO^KA RAZRYWA 1–GO RODA W SLU^AE I NEUBYWA@]EJ, I NEWOZRASTA@]EJ FUNKCII f.
tEOREMA 4 (KRITERIJ NEPRERYWNOSTI MONOTONNOJ FUNKCII). pUSTX f : [a, b] → R — MONOTONNAQ FUNKCIQ. fUNKCIQ f NEPRERYWNA NA OTREZKE [a, b] OBRAZ f([a, b]) OTREZKA SAM QWLQETSQ OTREZKOM S KONCAMI f(a) I f(b).
dOK–WO. ” ”: WWIDU MONOTONNOSTI f WSE ZNA^ENIQ, KOTORYE FUNKCIQ PRINIMAET NA OTREZKE [a, b], LEVAT MEVDU ZNA^ENIQMI f(a) I f(b), KOTORYE ONA PRINIMAET W KONCAH OTREZKA. sOGLASNO TEOREME O PROMEVUTO^NOM ZNA^ENII ONA OBQZANA PRI - NIMATX I WSE ZNA^ENIQ MEVDU f(a) I f(b). tAKIM OBRAZOM, MNOVESTWO ZNA^ENIJ FUNKCII QWLQETSQ OTREZKOM S KONCAMI f(a) I f(b).
” ”: IZ OPREDELENIQ SLEDUET: FUNKCIQ f NEPRERYWNA NA OTREZKE [a, b]
f(c) = f(c + 0) PRI c [a, b) I f(c) = f(c − 0) PRI c (a, b].
53
pUSTX f — NEUBYWA@]AQ FUNKCIQ S OBLASTX@ OPREDELENIQ [a, b]. pRI c (a, b]
OGRANI^EN SWERHU ZNA^ENIEM
MNOVESTWO f [a, S) |
f(b). rASSUVDAQ KAK PRI DOKA- |
|
ZATELXSTWE PREDYDU]EJ TEOREMY, DOKAZYWAEM SU]ESTWOWANIE KONE^NOGO PREDELA |
||
f(c − 0). |
|
|
pRI a 6 a1 < c − x < c < a2 6 b IMEEM f(a1) 6 f(c − |
x) 6 f(c) 6 f(a2). |
|
pEREHODQ W \TIH NERAWENSTWAH K PREDELU |
x → 0+, POLU^AEM |
f(a1) 6 f(c − x) 6 |
sLEDOWATELXNO, PRI f(c−0) < f(c) INTERWAL (f(c−0), f(c)) NE LEVIT W OBRAZE f([a, b]), A \TO PROTIWORE^IT USLOWI@. pO\TOMU f(c − 0) = f(c).
aNALOGI^NO DOKAZYWAETSQ RAWENSTWO f(c) = f(c+ 0) PRI c [a, b) I RAZBIRAETSQ SLU^AJ NEWOZRASTA@]EJ FUNKCII. .
18.3o NEPRERYWNOSTI OBRATNOJ FUNKCII
tEOREMA 5 (O SU]ESTWOWANII I NEPRERYWNOSTI OBRATNOJ FUNKCII).
1) eSLI FUNKCIQ f : E → R — STROGO MONOTONNA NA MNOVESTWE E R, TO f IMEET OBRATNU@ FUNKCI@ f−1 : Y → E, OPREDELENNU@ NA MNOVESTWE Y = f(E) ZNA^ENIJ FUNKCII f. fUNKCIQ f−1 MONOTONNA I IMEET NA Y TOT VE WID MONOTONNOSTI, KAKOJ IMEET FUNKCIQ f NA MNOVESTWE E.
2) eSLI, KROME TOGO, E ESTX PROMEVUTOK, A FUNKCIQ f NEPRERYWNA NA NEM, TO MNOVESTWO Y ESTX PROMEVUTOK, I FUNKCIQ f−1 NEPRERYWNA NA Y .
dOK–WO. 1) oTOBRAVENIE f : E → Y = |
f(E) S@R_EKTIWNO PO OPREDELENI@. |
||
pUSTX DLQ OPREDELENNOSTI f WOZRASTAET NA E. tOGDA |
|
||
x1 E x2 E |
x1 < x2 |
f(x1) < f(x2) . |
(4) |
tAKIM OBRAZOM, OTOBRAVENIE f W RAZLI^NYH TO^KAH PRINIMAET RAZLI^NYE ZNA^E - NIQ, T.E. ONO IN_EKTIWNO. sLEDOWATELXNO, f BIEKTIWNO, A ZNA^IT, OPREDELENO OBRAT- NOE OTOBRAVENIE f−1 : Y → E, ZADAWAEMOE FORMULOJ x = f−1(y), ESLI y = f(x).
sOPOSTOWLQQ OPREDELENIE f−1 S SOOTNO[ENIEM (4), POLU^AEM SOOTNO[ENIE
y1 Y y2 Y f−1(y1) < f−1(y2) y1 < y2 ,
OZNA^A@]EE, ^TO FUNKCIQ f−1 WOZRASTAET NA OBLASTI SWOEGO OPREDELENIQ .
2) pUSTX y |
, y |
2 |
Y |
= f(E) I y |
1 |
= y |
. tOGDA x |
i |
= f |
−1 |
(y |
) |
|
|
E, i = 1, 2, |
||||
1 |
|
|
|
6 |
2 |
|
|
|
i |
|
|
|
|
|
|
||||
I x1 6= x2. pUSTX DLQ OPREDELENNOSTI x1 |
|
< x2. tAK KAK x1 |
, x2 E, |
A E ESTX |
|||||||||||||||
PROMEVUTOK, TO [x1, x2] |
E. pO\TOMU FUNKCIQ f NEPRERYWNA NA OTREZKE [x1, x2]. |
||||||||||||||||||
pO KRITERI@ NEPRERYWNOSTI MONOTONNOJ FUNKCII OBRAZ f |
[x1, x2] |
|
ESTX OTREZOK |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ILI |
[y2 |
, y1]) |
POL |
- |
||
S KONCAMI f(x1) = y1, f(x2) = y2. sLEDOWATELXNO, OTREZOK [y1, y2] ( |
|
|
|
||||||||||||||||
NOSTX@ LEVIT W Y , A f−1 — MONOTONNAQ NA \TOM OTREZKE FUNKCIQ, OBRAZ KOTOROJ
QWLQETSQ OTREZOK [x1, x2], PRI^EM x1, x2 — OBRAZY KONCOW OTREZKA [y1, y2]. pO KRI- TERI@ NEPRERYWNOSTI MONOTONNOJ FUNKCII FUNKCIQ f−1 NEPRERYWNA NA OTREZKE
[y1, y2].
pOSKOLXKU y1, y2 — PROIZWOLXNYE TO^KI IZ Y , TO Y — PROMEVUTOK, A FUNKCIQ f−1 NEPRERYWNA W KAVDOJ TO^KE y IZ Y . dEJSTWITELXNO, TAK KAK PROMEVUTKAMI
QWLQ@TSQ TOLXKO INTERWALY, POLUINTERWALY I OTREZKI (SM. ZADA^U 2 IZ §4), TO LIBO y — WNUTRENNQQ TO^KA PROMEVUTKA Y , LIBO Y ESTX POLUINTERWAL ILI OTREZOK,
54
A y — EGO KONCEWAQ TO^KA. w PERWOM SLU^AE SU]ESTWU@T TO^KI y1 I y2 IZ Y SLEWA I SPRAWA OT y: y1 < y < y2. tOGDA IZ NEPRERYWNOSTI FUNKCII f−1 NA OTREZKE [y1, y2]
(SM. PREDYDU]IJ ABZAC) SLEDUET NEPRERYWNOSTX \TOJ FUNKCII W TO^KE y. eSLI y — KONCEWAQ TO^KA PROMEVUTKA Y , TO RASSMATRIWAQ KAKU@–LIBO DRUGU@ TO^KU
y1 IZ Y , DOKAZYWAEM NEPRERYWNOSTX FUNKCII f−1 NA OTREZKE [y1, y] |
(ILI [y, y1]), A |
||||||||||||
ZNA^IT, FUNKCIQ f−1 : Y |
→ |
E NEPRERYWNA I W KONCEWOJ TO^KE y |
|
Y . . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
−π2 , |
π2 . |
||||
pRIMER 4. |
fUNKCIQ y = sin x WOZRASTAET I NEPRERYWNA NA OTREZKE |
||||||||||||
|
|
|
|
|
|
|
π |
|
= |
|
π |
|
|
oGRANI^ENIE \TOJ FUNKCII NA \TOT OTREZOK IMEET OBRATNU@ FUNKCI@ x |
|
arcsin y, |
|||||||||||
[−1, 1]. |
, |
|
|
sin − |
2 |
, sin |
2 |
|
= |
||||
OPREDELENNU@ |
|
NEPRERYWNU@ I WOZRASTA@]U@ NA OTREZKE |
|
|
|
|
|
|
|
|
|
||
pRIMER 5. aNALOGI^NO, OGRANI^ENIE FUNKCII y = cos x NA OTREZOK [0, π] ESTX UBYWA@]AQ NEPRERYWNAQ FUNKCIQ, KOTORAQ IMEET OBRATNU@ FUNKCI@ x = arccos y, OPREDELENNU@, NEPRERYWNU@ I UBYWA@]U@ NA OTREZKE [−1, 1].
pRIMER 6. oGRANI^ENIE FUNKCII y = tg x NA INTERWAL |
−π2 , π2 |
|
ESTX WOZRA- |
|||
STA@]AQ OT −∞ DO ∞ NEPRERYWNAQ FUNKCIQ, KOTORAQ W |
SILU TEOREMY |
5 |
IMEET |
|||
|
|
|
|
|
||
OBRATNU@ FUNKCI@ x = arctg y, OPREDELENNU@, NEPRERYWNU@ I WOZRASTA@]U@ NA WSEJ PRQMOJ.
zADA^A 1. pRIWEDITE PRIMER NEPRERYWNOJ NEMONOTONNOJ FUNKCII, IME@]EJ OBRATNU@.
19 pROIZWODNAQ FUNKCII
sM. [z: STR. 170–187].
19.1pROIZWODNAQ I EE MEHANI^ESKIJ SMYSL
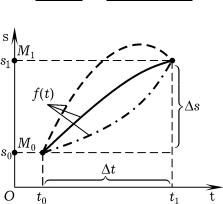
pRIMER 1 (cKOROSTX DWIVENIQ). rASSMOTRIM PRQMOLINEJNOE DWIVENIE TO^E^- NOJ MASSY. pUSTX FUNKCIQ s = f(t) OPISYWAET ZAWISIMOSTX OT WREMENI t RASSTOQ- NIQ s, PROJDENNOGO TO^KOJ (RIS. 18), PRI^EM W MOMENT WREMENI t0 TO^KA ZANIMAET POLOVENIE M0 I RASPOLAGAETSQ NA RASSTOQNII s0 = f(t0) OT O. ~EREZ PROMEVUTOK WREMENI t = t1 − t0 TO^KA OKAVETSQ W POLOVENII M1, A PROJDENNOE RASSTOQNIE BUDET s = s1 − s0, GDE s1 = f(t1). w DANNOM SLU^AE RAZNOSTNOE OTNO[ENIE
s |
= |
s1 − s0 |
= |
f(t1) − f(t0) |
= vSR |
|
t1 − t0 |
|
|||
t |
|
|
t1 − t0 |
||
rIS. 18
55

RAWNO SREDNEJ SKOROSTI vSR, S KOTOROJ DOLVNA BYLA BY RAWNOMERNO DWIGATXSQ TO^KA
W TE^ENIE PROMEVUTKA WREMENI t, ^TOBY PROJTI RASSTOQNIE |
s. pRI NERAWNOMER- |
NOM DWIVENII ZNA^ENIE vSR ZAWISIT KAK OT t0, TAK I OT WYBORA |
t, NO \TO ZNA^ENIE |
BUDET ODINAKOWO DLQ L@BYH ZAWISIMOSTEJ , GRAFIKI KOTORYH PROHODQT ^EREZ TO^KI (t0; s0) I (t1; s1) (SM. RIS. 18, SPLO[NAQ, [TRIHOWAQ I [TRIHPUNKTIRNYE KRIWYE).
~TOBY POLU^ITX BOLEE TO^NOE PREDSTAWLENIE O SKOROSTI TO^KI W MOMENT WRE -
MENI t0, SLEDUET UMENX[ATX PROMEVUTOK WREMENI t I W PREDELE USTREMITX EGO K NUL@ (Δt → 0). tOGDA PREDEL (ESLI, KONE^NO, ON SU]ESTWUET)
v = lim |
s |
= lim |
f(t) − f(t0) |
||
t |
|
t − t0 |
|||
t→0 |
t→t0 |
||||
ESTESTWENNO NAZWATX MGNOWENNOJ SKOROSTX@ TO^KI W MOMENT WREMENI t0. .
pUSTX a — PREDELXNAQ TO^KA MNOVESTWA f : E → R W TO^KE a NAZYWA@T PREDEL PRI USLOWII, ^TO \TOT PREDEL SU]ESTWUET), T.E.
E, a E. pROIZWODNOJ FUNKCII x → 0 RAZNOSTNOGO OTNO[ENIQ (PRI
lim |
f(a) |
= lim |
f(x) − f(a) |
. |
|
x |
|
|
|||
x→0 |
x→a |
x − a |
|||
oBOZNA^ENIQ: f0(a), y0(a), yx0 , dy/dx ILI PROSTO y0.
pRIMER 2. y = xs, GDE s — L@BOE OTLI^NOE OT NULQ DEJSTWITELXNOE ^ISLO . oBLASTX E OPREDELENIQ \TOJ FUNKCII ZAWISIT OT ZNA^ENIQ s:
1)E = R PRI s = nk > 0 I NE^ETNOM n (nk — NESOKRATIMAQ DROBX);
2)E = {x 6= 0} PRI s = nk < 0 I NE^ETNOM n;
3)E = {x > 0} PRI s = nk > 0 I ^ETNOM n;
4)E = {x > 0} W OSTALXNYH SLU^AQH.
pRI x 6= 0 W OBLASTI OPREDELENIQ FUNKCII IMEEM
y0 = lim |
y |
= |
lim |
(x + |
x)s − xs |
= xs lim |
(1 + |
xx )s − 1 |
|
= xs lim |
s xx |
= sxs−1. |
|
x |
|
x |
|
|
x |
|
x |
||||||
x→0 |
|
x→0 |
x→0 |
|
|
x→0 |
|
||||||
oTMETIM, ^TO PRI x = 0 OBLASTI OPREDELENIQ y I y0 SOWPADA@T: |
|
|
|||||||||||||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x > 0 s — L@BOE; |
|
|
|
|
|
|
|
|
|
|
|
k−n |
|
|
|
|
|
|
|||||
|
k |
|
|
|
NE^ETNOE |
|
|
|
|
|
|
|
TAKOGO VE TIPA |
|
|
||||||||
x < 0 s = n |
, n — |
s − |
1 = |
— |
. |
|
|||||||||||||||||
|
|
|
k |
|
|
|
|
n |
|
|
|
||||||||||||
w TO^KE x = 0 PRI s = n |
> 0 I NE^ETNOM n IMEEM (PRI ^ETNOM n PREDEL SPRAWA) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
|
(Δx)s |
|
|
|
|
0 |
PRI |
s > 1 |
|
|
||
|
|
y0 |
|
lim |
|
|
lim |
= |
1 |
PRI |
s = 1 |
|
|
||||||||||
|
|
= |
|
|
= |
|
x |
|
|
||||||||||||||
|
|
|
|
x |
→ |
0 |
|
x 0 |
|
|
|
|
s < 1. |
|
|
||||||||
|
|
|
|
|
|
|
|
x |
→ |
|
|
∞ |
PRI |
|
|
||||||||
s |
|
|
s |
1 |
|
|
|
|
|
|
|
|
OPREDELENA PRAWAQ ^ASTX RAWENSTWA |
|
|||||||||
pO\TOMU (x )0 = sx − |
|
W TEH TO^KAH, GDE |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
mEHANI^ESKIJ SMYSL PROIZWODNOJ FUNKCII s = f(t), OPISYWA@]EJ DWI-
VENIE TO^KI W ZAWISIMOSTI OT WREMENI t, SOSTOIT W TOM, ^TO ZNA^ENIE PROIZWODNOJ f0(t0) RAWNO MGNOWENNOJ SKOROSTI W MOMENT WREMENI t0.
56
19.2gEOMETRI^ESKIJ SMYSL PROIZWODNOJ
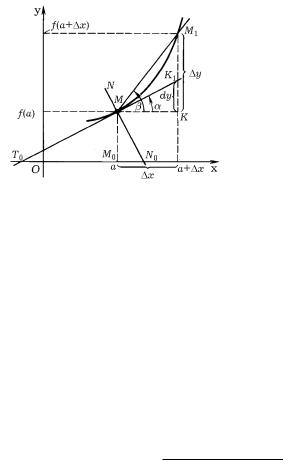
pUSTX GRAFIK FUNKCII y = f(x) W OKRESTNOSTI TO^KI a IMEET WID, POKAZANNYJ
. |
|
|
I |
|
|
|
PRQMU@ |
|
|
M1 |
|
|
|||||
NA RIS. 19. pROWEDEM ^EREZ TO^KI M a; f(a) |
|
|
M1 |
a + x; f(a + x) |
|
, NA- |
||
ZYWAEMU@ SEKU]EJ |
pRI PEREME]ENII TO^KI |
|
PO KRIWOJ MENQETSQ I POLOVENIE |
|||||
|
|
|
|
|
||||
SEKU]EJ.
rIS. 19
eSLI SU]ESTWUET PREDELXNOE POLOVENIE SEKU]EJ MM1, KOGDA TO^KA M1, PERE- ME]AQSX WDOLX KRIWOJ, STREMITSQ K TO^KE M, TO PRQMU@, K KOTOROJ STREMITSQ SEKU]AQ, NAZYWA@T KASATELXNOJ K GRAFIKU FUNKCII y = f(x) W TO^KE M.
nAJDEM UGLOWOJ KO\FFICIENT KASATELXNOJ K GRAFIKU y = f(x) W TO^KE
M a; f(a) . iZ RIS. 19 SLEDUET, ^TO UGLOWOJ KO\FFICIENT SEKU]EJ MM1 SOWPADAET
S RAZNOSTNYM OTNO[ENIEM, T.E. tg β = y/ x. dLQ POLU^ENIQ UGLOWOGO KO\FFICIENTA KASATELXNOJ NUVNO PEREJTI K PREDELU W \TOM RAZNOSTNOM OTNO[ENII PRI x → 0. tAK KAK PRI \TOM β → α, TO W SILU NEPRERYWNOSTI FUNKCII tg x UGLOWOJ
KO\FFICIENT KASATELXNOJ RAWEN
k = tg α = lim tg β = |
lim |
y |
= |
lim |
f(a + |
x) − f(a) |
= f0(a). |
x |
|
x |
|||||
x→0 |
x→0 |
|
x→0 |
|
|||
gEOMETRI^ESKIJ SMYSL: PROIZWODNAQ f0(a) RAWNA UGLOWOMU KO\FFICIENTU KA-
SATELXNOJ K GRAFIKU FUNKCII y = f(x) W TO^KE M a; f(a) .
uRAWNENIE KASATELXNOJ K GRAFIKU FUNKCII: y − f(a) = f0(a)(x − a).
pRQMU@, PROHODQ]U@ ^EREZ TO^KU M PERPENDIKULQRNO KASATELXNOJ, NAZYWA@T
NORMALX@ K GRAFIKU FUNKCII y = f(x) W TO^KE M (NA RIS. 19 \TO PRQMAQ NN0). uRAWENIE NORMALI IMEET WID y −f(a) = −(x−a)/f0(a), ESLI f0(a) 6= 0, I WID x = a,
ESLI f0(a) = 0.
pUSTX FUNKCIQ y = f(x) NE OPREDELENA NA (a − δ, a) DLQ NEKOTOROGO δ. tOGDA PRI WY^ISLENII PREDELA RAZNOSTNOGO OTNO[ENIQ y/ x PRIHODITSQ OGRANI^ITXSQ PRIBLIVENIEM x K NUL@ TOLXKO SPRAWA. pRI SU]ESTWOWANII TAKOGO ODNOSTORONNEGO PREDELA EGO NAZYWA@T ODNOSTORONNEJ PROIZWODNOJ W TO^KE a SPRAWA
I OBOZNA^A@T f+0 (a). aNALOGI^NO OPREDELQETSQ ODNOSTORONNQQ PROIZWODNAQ W TO^KE a SLEWA f−0 (a). w TAKIH SITUACIQH (RIS. 20 I RIS. 21) W TO^KE a GRAFIK FUNK-
CII IMEET ODNOSTORONN@@ KASATELXNU@, T.E. PREDELXNOE POLOVENIE SEKU]EJ SU]ESTWUET TOLXKO, KOGDA TO^KA M1 NAHODITSQ SPRAWA (SLEWA) OT TO^KI M.
57
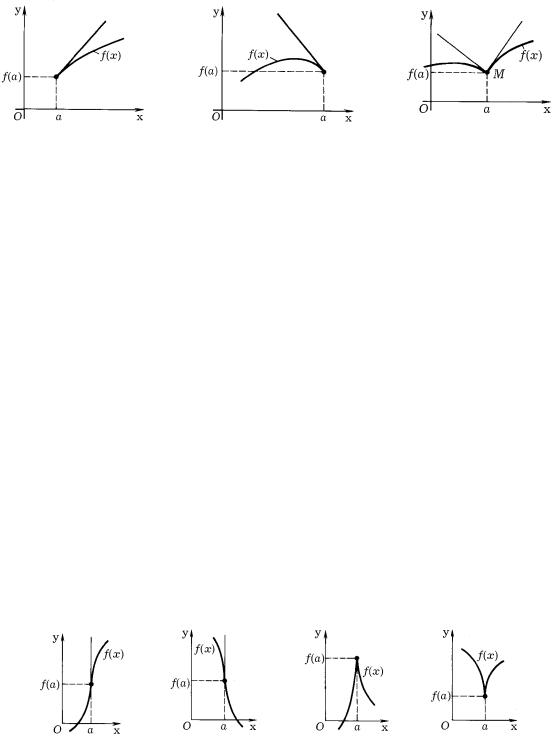
rIS. 20 rIS. 21 rIS. 22
mOVET OKAZATXSQ, ^TO W NEKOTOROJ WNUTRENNEJ TO^KE x = a TOGO PROMEVUTKA, W KOTOROM OPREDELENA I NEPRERYWNA FUNKCIQ y = f(x), SU]ESTWU@T NE RAWNYE MEVDU SOBOJ ODNOSTORONNIE PREDELY RAZNOSTNOGO OTNO[ENIQ y/ x. iH TOVE NAZYWA@T ODNOSTORONNIMI PROIZWODNYMI FUNKCII W TO^KE a. w \TOM SLU^AE W SOOTWETSTWU- @]EJ TO^KE GRAFIKA FUNKCII BUDUT SU]ESTWOWATX ODNOSTORONNIE KASATELXNYE ,
PRI \TOM OBRAZU@]IE, WOOB]E GOWORQ, NEKOTORYJ UGOL (RIS. 22). tO^KU M a, f(a)
NAZYWA@T UGLOWOJ TO^KOJ (ILI TO^KOJ IZLOMA) GRAFIKA FUNKCII.
zADA^A 1. pRIWEDITE PRIMER \LEMENTARNOJ FUNKCII S TO^KOJ IZLOMA .
oDIN ILI OBA ODNOSTORONNIH PREDELA RAZNOSTNOGO OTNO[ENIQ y/ x W TO^- KE a MOGUT BYTX BESKONE^NYMI. tOGDA GOWORQT O BESKONE^NOJ ODNOSTORONNEJ PROIZWODNOJ FUNKCII y = f(x) SLEWA ILI SPRAWA W TO^KE a (W OTLI^IE OT RAS-
SMOTRENNYH WY[E SLU^AEW KONE^NOJ ODNOSTORONNEJ PROIZWODNOJ). dLQ NE-
PRERYWNOJ FUNKCII BESKONE^NAQ ODNOSTORONNQQ PROIZWODNAQ MOVET BYTX TOLXKO OPREDELENNOGO ZNAKA (LIBO +∞, LIBO −∞). eSLI ZNAKI BESKONE^NYH ODNOSTORON-
NIH PROIZWODNYH FUNKCII I SLEWA I SPRAWA W NEKOTOROJ TO^KE a SOWPADA@T, TO W \TOJ TO^KE DANNAQ FUNKCIQ IMEET BESKONE^NU@ PROIZWODNU@ OPREDELENNOGO ZNAKA (POLOVITELXNU@ NA RIS. 23 I OTRICATELXNU@ NA RIS. 24). w \TOM SLU^AE KASATELXNAQ K GRAFIKU FUNKCII W SOOTWETSTWU@]EJ TO^KE SU]ESTWUET I QWLQETSQ WERTIKALXNOJ. eSLI VE ZNAKI BESKONE^NYH ODNOSTORONNIH PROIZWODNYH RAZLI^ -
NY, TO SOOTWETSTWU@]U@ TO^KU GRAFIKA FUNKCII NAZYWA@T TO^KOJ ZAOSTRENIQ
(TO^KOJ WOZWRATA) (RIS. 25 I RIS. 26).
rIS. 23 |
rIS. 24 |
rIS. 25 |
rIS. 26 |
zADA^A 2. pRIWEDITE PRIMERY \LEMENTARNYH FUNKCIJ A) S BESKONE^NOJ PRO- IZWODNOJ I B) S TO^KOJ WOZWRATA.
pRIMER 3. rASSMOTRIM FUNKCI@
|
0, |
x = 0. |
f(x) = |
x sin(1/x), |
x 6= 0; |
58
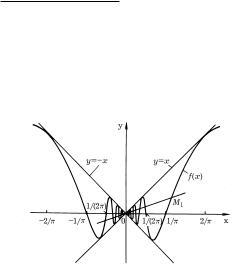
oNA NEPRERYWNA W L@BOJ TO^KE x R, NO NE IMEET W TO^KE x = 0 DAVE ODNOSTORON- NIH PROIZWODNYH. dEJSTWITELXNO, RAZNOSTNOE OTNO[ENIE W \TOJ TO^KE
f(0 + x) − f(0) |
= |
f(Δx) |
= sin |
1 |
|
x |
x |
x |
|||
|
|
NE STREMITSQ NI K KAKOMU PREDELU PRI x → 0. sEKU]AQ OM1 (RIS. 27), ISHODQ]AQ IZ NA^ALA KOORDINAT, NE IMEET PREDELXNOGO POLOVENIQ PRI STREMLENII TO^KI M1 K TO^KE O, TAK ^TO W NA^ALE KOORDINAT NE SU]ESTWUET K KRIWOJ KASATELXNOJ (HOTQ BY ODNOSTORONNEJ).
rIS. 27
19.3dIFFERENCIRUEMOSTX FUNKCIJ
pUSTX a E — PREDELXNAQ TO^KA MNOVESTWA E R. fUNKCI@ f : E → R NA- ZYWA@T DIFFERENCIRUEMOJ W TO^KE a, ESLI PRIRA]ENIE \TOJ FUNKCII W \TOJ TO^KE MOVNO PREDSTAWITX W WIDE SUMMY DWUH SLAGAEMYH , PERWOE — LINEJNOE OT-
NOSITELXNO x, WTOROE — o–MALOE OT |
x: |
|
f(a) = L |
x + α(Δx)Δx, |
(1) |
GDE L — ^ISLO, NE ZAWISQ]EE OT x, a + x E, A FUNKCIQ α(Δx) QWLQETSQ
BESKONE^NO MALOJ PRI x → 0 (L@BOE o–MALOE OT |
x MOVNO PREDSTAWITX W WI- |
DE α(Δx)Δx). pRI \TOM LINEJNU@ OTNOSITELXNO |
x ^ASTX PRIRA]ENIQ FUNKCII |
f NAZYWA@T DIFFERENCIALOM FUNKCII f I OBOZNA^A@T ^EREZ df ILI df(a),
dy(a, x) I T.P.
zAME^ANIE. eSLI f(x) = x, TO dx = x. pO\TOMU DIFFERENCIAL ARGUMENTA x OTOVDESTWLQ@T S EGO PRIRA]ENIEM x, T.E. POLAGA@T dx = x.
rAWNOSILXNOSTX DIFFERENCIRUEMOSTI FUNKCII W TO^KE I SU]ESTWOWANIQ W \TOJ TO^KE KONE^NOJ PROIZWODNOJ DANNOJ FUNKCII USTANAWLIWAET SLEDU@]AQ TEOREMA .
tEOREMA 1. 1) dLQ DIFFERENCIRUEMOSTI FUNKCII y = f(x) W TO^KE a NEOBHODI- MO I DOSTATO^NO, ^TOBY ONA IMELA W \TOJ TO^KE KONE^NU@ PROIZWODNU@ (USLOWIE DIFFERENCIRUEMOSTI FUNKCII).
2) df(a) = f0(a)dx.
dOK–WO. 1) n E O B H O D I M O S T X. eSLI FUNKCIQ DIFFERENCIRUEMA W TO^KE a, T.E. SPRAWEDLIWO (1), TO PRI x 6= 0 POLU^IM f(a)/ x = L + α(Δx). oTS@DA
59

SLEDUET, ^TO SU]ESTWUET KONE^NYJ PREDEL
lim |
f(a) |
= L, |
||
x |
|
|||
x→0 |
|
|||
T.E. SU]ESTWUET KONE^NAQ PROIZWODNAQ f0(a) I L = f0(a).
d O S T A T O ^ N O S T X. pUSTX FUNKCIQ y = f(x) IMEET W TO^KE a KONE^NU@ PRO- IZWODU@ f0(a), T.E. SU]ESTWUET KONE^NYJ PREDEL
lim |
f(a) |
= f0(a). |
||
x |
|
|||
x→0 |
|
|||
pO TEOREME O SWQZI FUNKCII, EE PREDELA I B.M. MOVNO NAPISATX f(a)/ x = f0(a)+
GDE α(Δx) — B.M. PRI oTS@DA f(a) = f0(a)Δx+ α(Δx)Δx, ^TO
W SILU OPREDELENIQ OZNA^AET DIFFERENCIRUEMOSTX FUNKCII y = f(x) W TO^KE a. 2) w HODE DOKAZATELXSTWA 1) USTANOWLENO, ^TO DLQ DIFFERENCIRUEMOJ W TO^KE a
FUNKCII y = f(x) WYPOLNENO RAWENSTWO L = f0(a). pO\TOMU df(a) = f0(a)dx. .
zAME^ANIE. fOMULA dy = y0dx OB_QSNQET, PO^EMU DLQ PROIZWODNOJ ISPOLXZU- ETSQ OBOZNA^ENIE y0 = dxdy .
uTWERVDENIE 1) TEOREMY 1 NAZYWA@T NEOBHODIMYM I DOSTATO^NYM USLOWIEM DIFFERENCIRUEMOSTI FUNKCII ODNOGO PEREMENNOGO. nEOBHODIMOE USLOWIE DIFFE- RENCIRUEMOSTI FUNKCII W TO^KE USTANAWLIWAET SLEDU@]AQ TEOREMA .
tEOREMA 2 (O SWQZI DIFFERENCIRUEMOSTI I NEPRERYWNOSTI FUNKCII). eSLI FUNKCIQ y = f(x) DIFFERENCIRUEMA W TO^KE x = a, TO ONA NEPRERYWNA W \TOJ TO^KE.
dOK–WO. tAK KAK FUNKCIQ y = f(x) DIFFERENCIRUEMA W TO^KE a, EE PRIRA]ENIE PREDSTAWIMO W WIDE f(a) = L x + o(Δx). oTS@DA SRAZU SLEDUET f(a) → 0 PRI
x → 0, ^TO RAWNOSILXNO NEPRERYWNOSTI FUNKCII y = f(x) W TO^KE a. .
pRIMER 4. fUNKCIQ y = |x| NEPRERYWNA, NO NEDIFFERENCIRUEMA W TO^KE x = 0. a ZNA^IT, UTWERVDENIE, OBRATNOE UTWERVDENI@ TEOREMY 2, NEWERNO, T.E. IZ NEPRERYWNOSTI FUNKCII W TO^KE NE SLEDUET EE DIFFERENCIRUEMOSTX W \TOJ TO^KE .
fUNKCI@, DIFFERENCIRUEMU@ W KAVDOJ TO^KE MNOVESTWA X R, NAZYWA- @T DIFFERENCIRUEMOJ NA MNOVESTWE X. eSLI FUNKCIQ DIFFERENCIRUEMA W KAVDOJ TO^KE SWOEJ OBLASTI OPREDELENIQ , TO EE NAZYWA@T PROSTO DIFFERENCI-
RUEMOJ.
gEOMETRI^ESKIJ SMYSL DIFFERENCIALA FUNKCII (SM. RIS. 19): DIFFE-
TO^KI NA KASATELXNOJ K GRAFIKU FUNKCII f, |
|
|
ORDINATY |
x |
RENCIAL FUNKCII f W TO^KE a RAWEN PRIRA]ENI@ W TO^KE M a; f(a) SOOTWETSTWU@]EMU PRIRA]ENI@
ARGUMENTA.
20 pRAWILA DIFFERENCIROWANIQ
sM. [z, S. 189–197] ILI [iW. §2.1–2.3, STR. 36–51].
dIFFERENCIROWANIE — OPERACIQ NAHOVDENIQ PROIZWODNOJ.
60
