MAiu9

20.1aRIFMETI^ESKIE PRAWILA DIFFERENCIROWANIQ .

tEOREMA 1. pUSTX FUNKCII u(x) I v(x) DIFFERENCIRUEMY W TO^KE x. tOGDA W \TOJ TO^KE DIFFERENCIRUEMY IH SUMMA, PROIZWEDENIE I ^ASTNOE (POSLEDNEE PRI USLOWII v(x) 6= 0), A TAKVE IH PROIZWEDENIE NA KONSTANTU C, PRI^EM SPRAWEDLIWY RAWENSTWA (ZDESX OBOZNA^ENIQ ARGUMENTA x OPU]ENO):

pRI DOKAZATELXSTWE ISPOLXZU@TSQ OPREDELENIE PROIZWODNOJ I PRAWILA PRE - DELXNOGO PEREHODA DLQ SUMMY, PROIZWEDENIQ I ^ASTNOGO DWUH FUNKCIJ. dOKAVEM FORMULY 3 I 4. fORMULY 1 I 2 DOKAZYWA@TSQ ANALOGI^NO.

3) pUSTX y(x) = u(x)v(x). dADIM ARGUMENTU x PRIRA]ENIE x. tOGDA FUNKCII u, v I y POLU^AT SOOTWETSTWENNO PRIRA]ENIQ

oTS@DA PRI x 6= 0 IMEEM

iZ DIFFERENCIRUEMOSTI FUNKCII v W TO^KE x SLEDUET EE NEPRERYWNOSTX W \TOJ TO^KE, T.E.

tAK KAK FUNKCII u I v DIFFERENCIRUEMY W TO^KE x, W \TOJ TO^KE SU]ESTWU@T KONE^NYE PREDELY

w SILU (3), (1), (2) I PRAWIL PREDELXNOGO PEREHODA DLQ SUMMY I PROIZWEDENIQ FUNKCIJ SU]ESTWUET KONE^NYJ PREDEL

T.E. W TO^KE x SU]ESTWUET KONE^NAQ PROIZWODNAQ FUNKCII y(x) = u(x)v(x), RAWNAQ

y0 = (uv)0 = u0v + uv0.

4) eSLI W TO^KE x WYPOLNENO USLOWIE v(x) 6= 0, TO W \TOJ TO^KE OPREDELENA

61

sOGLASNO (3), (2), (4) I PRAWILAM PREDELXNOGO PEREHODA DLQ SUMMY I ^ASTNOGO FUNKCIJ, ZAKL@^AEM, ^TO SU]ESTWUET KONE^NYJ PREDEL

zADA^A 1. iSPOLXZUQ FORMULU 4 DANNOJ TEOREMY, WYWEDITE FORMULU DLQ PRO- IZWODNOJ tg x.

sLEDSTWIE 1. w USLOWIQH TEOREMY 1 IMEEM:

dOK–WO. 3: d(uv) = (uv)0dx = (u0v + uv0)dx = vu0dx + uv0dx = v du + u dv.

oSTALXNYE FORMULY DOKAZYWA@TSQ ANALOGI^NO .

20.2pROIZWODNAQ SLOVNOJ FUNKCII

tEOREMA 2 (PROIZWODNAQ SLOVNOJ FUNKCII). pUSTX FUNKCIQ g : X → Z

DIFFERENCIRUEMA W TO^KE a X, A FUNKCIQ f : Z → R DIFFERENCIRUEMA W SO- OTWETSTWU@]EJ TO^KE b = g(a) Z. tOGDA SLOVNAQ FUNKCIQ f ◦ g : X → R DIFFERENCIRUEMA W TO^KE a I

(f ◦ g)(a) = fz0 g(a) gx0 (a).

dOK–WO. pUSTX PRIRA]ENI@ x ARGUMENA x W TO^KE a SOOTWETSTWUET PRIRA- ]ENIE z = g(a + x) − g(a) FUNKCII z = g(x), A z, W SWO@ O^EREDX, WYZYWAET PRIRA]ENIE y = f(b + z) − f(b) FUNKCII y = f(z). tAK KAK FUNKCII y = f(z)

I z = g(x) DIFFERENCIRUEMY W TO^KAH b I a SOOTWETSTWENNO, TO IH PRIRA]ENIQ MOVNO ZAPISATX W WIDE

y = f0(b) + α(Δz) z, z = g0(a) + β(Δx) x,

sLEDSTWIE 2 (INWARIANTNOSTX FORMY PERWOGO DIFFERENCIALA). fOR-

MULA DLQ DIFFERENCIALA FUNKCII dy = f0(u)du ODINAKOWA DLQ SLU^AQ, KOGDA u —

62

ARGUMENT \TOJ FUNKCII, I DLQ SLU^AQ, KOGDA u — FUNKCIQ KAKOGO–LIBO DRUGOGO ARGUMENTA.

dOK–WO. eSLI u — ARGUMENT FUNKCII f, TO UKAZANNAQ FORMULA SLEDUET IZ FOR- MULY SWQZI PROIZWODNOJ I DIFFERENCIALA (SM. ^ASTX 2 TEOREMY 1 IZ PREDYDU]EGO PARAGRAFA).

pUSTX u — FUNKCIQ ARGUMENTA x: u = g(x). pUSTX \TA FUNKCIQ DIFFERENCIRU- EMA W TO^KE a, A FUNKCIQ y = f(u) DIFFERENCIRUEMA W TO^KE b = g(a). pO TEOREME 2

DIFFERENCIRUEMA W TO^KE

SLOVNAQ FUNKCIQ F (x) = f g(x) a, A EE DIFFERENCIAL W TO^KE a ESTX

dy = dF (a) = F 0(a)dx = f0(b)g0(a)dx = f0(b)du,

GDE DWAVDY ISPOLXZOWALASX UKAZANNAQ FORMULA SWQZI PROIZWODNOJ I DIFFERENCI - ALA. t.E. PRI u = b W \TOM SLU^AE TAKVE POLU^AETSQ UKAZANNAQ W TEOREME FORMULA .

.

gEOMETRI^ESKAQ INTERPRETACIQ \TOGO SLEDSTWIQ. fORMULA DLQ DIFFE-

RENCIALA NE MENQETSQ PRI PEREHODE OT KOORDINATY u K KOORDINATE x. t.E. DIF- FERENCIAL NE ZAWISIT OT WYBORA SISTEMY KOORDINAT I HARAKTERIZUET SOBSTWENNO GEOMETRI^ESKIE SWOJSTWA FUNKCII, A NE EE PREDSTAWLENIE W KOORDINATAH.

iZ TEOREMY 2 SLEDUET FORMULA LOGARIFMI^ESKOJ PROIZWODNOJ: y0 = y(ln y)0. oNA PRIMENQETSQ W SLU^AE, KOGDA WY^ISLENIE (ln y)0 PRO]E, ^EM WY^ISLENIE y0.

20.3pROIZWODNAQ OBRATNOJ FUNKCII

tEOREMA 3 (PROIZWODNAQ OBRATNOJ FUNKCII). pUSTX FUNKCIQ y = f(x) W TO^-

KE x = a IMEET KONE^NU@ PROIZWODNU@ f0(a) 6= 0, I DLQ f(x) SU]ESTWUET OBRATNAQ FUNKCIQ x = g(y) NEPRERYWNAQ W SOOTWETSTWU@]EJ TO^KE y = b = f(a). tOGDA SU]ESTWUET PROIZWODNAQ g0(b) I

dOK–WO. dADIM ZNA^ENI@ y = b PRIRA]ENIE y. tOGDA FUNKCIQ x = g(y) TOVE

eSLI TEPERX y → 0, TO I x → 0 WWIDU NEPRERYWNOSTI FUNKCII x = g(y). nO TOGDA ZNAMENATELX W PRAWOJ ^ASTI STREMITSQ K PREDELU f0(a) 6= 0, T.E. SU]ESTWU- ET KONE^NYJ PREDEL PRAWOJ ^ASTI, RAWNYJ 1/f0(a). CLEDOWATELXNO, SU]ESTWUET KONE^NYJ PREDEL I LEWOJ ^ASTI. .

dADIM GEOMETRI^ESKU@ INTERPRETACI@ FORMULY (5). gRAFIKI RASSMOTRENNYH W TEOREME 3 FUNKCIJ y = f(x) I x = g(y) W KOORDINATNOJ PLOSKOSTI xOy SOWPA- DA@T (RIS. 28). pO\TOMU DLQ UGLOW α I β NAKLONA K OSQM KOORDINAT KASATELXNOJ ,

63

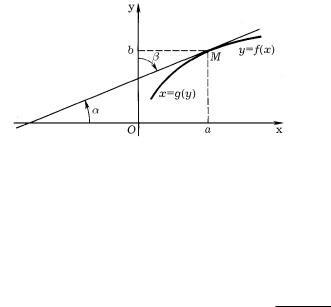
PROWEDENNOJ K KRIWOJ GRAFIKA W TO^KE M(a; b), SPRAWEDLIWO RAWENSTWO α+β = π/2, I, SOGLASNO GEOMETRI^ESKOMU SMYSLU PROIZWODNOJ ,

rIS. 28

pRIMER 2. fUNKCIQ y = arcsin x (x [−1, 1], y [−π/2, π/2]) QWLQETSQ

OBRATNOJ K FUNKCII x = sin y, IME@]EJ PROIZWODNU@ x0 = cos y > 0 DLQ WSEH y (−π/2, π/2). w TAKOM SLU^AE DLQ WSEH x (−1, 1), SOGLASNO TEOREME 3, SU]E- STWUET PROIZWODNAQ y0, PRI^EM

tO^KI x = ±1, PRINADLEVA]IE OBLASTI OPREDELENIQ FUNKCII y, ISKL@^ENY IZ RASSMOTRENIQ, POSKOLXKU W SOOTWETSTWU@]IH IM TO^KAH y = ±π/2 OBLASTI ZNA^E- NIJ \TOJ FUNKCII x0 = cos y = 0.

zADA^A 2. wYWEDITE FORMULY DLQ (ln x)0 I (arctg x)0.

zAME^ANIE. dLQ LU^[EGO ZAPOMINANIQ FORMUL DLQ PROIZWODNYH SLOVNOJ I OBRATNOJ FUNKCIJ IH LU^[E ZAPISATX TAK:

21 pRAWILA DIFFERENCIROWANIQ II

sM. [iW. §2.4–2.6, 4.1–4.2, 4.4–4.5, STR. 51–59, 78–88, 91–101].

21.1pROIZWODNYE I DIFFERENCIALY WYS[IH PORQDKOW

pUSTX FUNKCIQ DIFFERENCIRUEMA NA NEKOTOROM MNOVESTWE E.

IZWODNAQ f0(x) QWLQETSQ TOVE FUNKCIEJ ARGUMENTA x S OBLASTX@ OPREDELENIQ E. eSLI \TA NOWAQ FUNKCIQ f0(x) DIFFERENCIRUEMA, TO MOVNO NAJTI EE PROIZWODNU@,

NAZYWAEMU@ WTOROJ PROIZWODNOJ ISHODNOJ FUNKCII f(x), ILI PROIZWODNOJ WTOROGO PORQDKA, I OBOZNA^AEMU@ f00(x). w SWQZI S \TIM f0(x) DLQ OPREDELENNOSTI NAZYWA@T PERWOJ PROIZWODNOJ, ILI PROIZWODNOJ PERWOGO PORQDKA.

64

mEHANI^ESKIJ SMYSL WTOROJ PROIZWODNOJ. pUSTX FUNKCIQ s = f(t) OPI-

SYWAET ZAKON PRQMOLINEJNOGO DWIVENIQ TO^KI WO WREMENI t. tOGDA EE WTORAQ PRO- IZWODNAQ — \TO SKOROSTX IZMENENIQ SKOROSTI v = f0(t) TO^KI, T.E. USKORENIE.

eSLI f00(x) W SWO@ O^EREDX QWLQETSQ DIFFERENCIRUEMOJ FUNKCIEJ ARGUMENTA x, TO POSLEDU@]EE DIFFERENCIROWANIE f00(x) DAST TRETX@ PROIZWODNU@ f000(x) =

dIFFERENCIALOM n-GO PORQDKA FUNKCII y = f(x) NAZYWA@T DIFFEREN-

CIAL OT DIFFERENCIALA (n − 1)-GO PORQDKA W PREDPOLOVENII, ^TO dx POSTOQNNO. dIFFERENCIAL n-GO PORQDKA OBOZNA^A@T dny, dnf(x). pO OPREDELENI@

DA@T SWOJSTWOM INWARIANTNOSTI FORMY ZAPISI .

tEOREMA 1 (NEINWARIANTNOSTX FORMY WTOROGO DIFFERENCIALA). pUSTX y = f(z). tOGDA

1)ESLI z — ARGUMENT FUNKCII y, TO d2y = f00(z)dz2;

2)ESLI z — FUNKCIQ KAKOGO–LIBO DRUGOGO ARGUMENTA, TO d2y = fzz00 (z)dz2 +fz0(z)d2z.

dOK–WO. 1) pO FORMULE SWQZI PROIZWODNOJ I DIFFERENCIALA IMEEM

I d f0(z) = f00(z) dz PO OPREDELENI@ WTOROJ PROIZWODNOJ. sOGLASNO OPREDELENI@ WTOROGO DIFFERENCIALA

d2y = d(dy) = d f0(z) dz = d f0(z) dz = f00(z) dz2,

GDE dz MY S^ITAEM POSTOQNNYM.

2) eSLI z = g(x), TO IZ SWOJSTWA INWARIANTNOSTI FORMY PERWOGO DIFFERENCI - ALA IMEEM dy = f0(z) dz. pOD^ERKNEM, ^TO dz = g0(x) dx I z = g(x) NELXZQ S^ITATX W DANNOM SLU^AE NEZAWISIMYMI. pO\TOMU DIFFERENCIAL OT dy SLEDUET ISKATX KAK DIFFERENCIAL PROIZWEDENIQ:

d2y = d(dy) = d f0(z) dz = d f0(z) dz + f0(z) d(dz) = f00(z) dz2 + f0(z)d2z.

21.2dIFFERENCIROWANIE FUNKCIJ, ZADANNYH NEQWNO ILI

PARAMETRI^ESKI

pUSTX ZNA^ENIQ DWUH PEREMENNYH x I y SWQZANY URAWNENIEM F (x, y) = 0, GDE LEWAQ ^ASTX PREDSTAWLQET SOBOJ WYRAVENIE, SODERVA]EE x, y I \LEMENTARNYE FUNKCII. eSLI FUNKCIQ y = f(x) TAKOWA, ^TO PODSTANOWKA EE W URAWNENIE WMESTO y PREWRA]A- ET URAWNENIE W TOVDESTWO, TO GOWORQT, ^TO URAWNENIE ZADAET FUNKCI@ y = f(x)

NEQWNYM SPOSOBOM.

pRIMER 1. uRAWNENIE

NEQWNYM SPOSOBOM ZADAET DWE \LEMENTARNYE FUNKCII

√ √

f1(x) = R2 − x2 I f2(x) = − R2 − x2,

65

KOTORYE PRI y > 0 I y 6 0 SOOTWETSTWU@T DWUM POLUOKRUVNOSTQM RADIUSA R.

dLQ WY^ISLENIQ PROIZWODNOJ NEQWNO ZADANNOJ DIFFERENCIRUEMOJ FUNKCII SLE - DUET PRODIFFERENCIROWATX OBE ^ASTI RAWENSTWA F (x, y) = 0 PO x, ISPOLXZOWATX PRAWILO DIFFERENCIROWANIQ SLOVNOJ FUNKCII, I ZATEM RE[ITX POLU^ENNOE URAW- NENIE OTNOSITELXNO y0. dIFFERENCIRUQ POLU^ENNOE RAWENSTWO DLQ y0 E]E RAZ I

U^ITYWAQ WYRAVENIE DLQ PERWOJ PROIZWODNOJ , POLU^AEM WYRAVENIE DLQ y00. dLQ WY^ISLENIQ DIFFERENCIALA NEQWNO ZADANNOJ DIFFERENCIRUEMOJ FUNKCII SLEDUET WY^ISLITX DIFFERENCIAL OBEIH ^ASTEJ RAWENSTWA F (x, y) = 0, ISPOLXZUQ SWOJSTWA

DIFFERENCIALA, A ZATEM RE[ITX POLU^ENNOE URAWNENIE OTNOSITELXNO dy.

pRIMER 1. dIFFERENCIRUQ (1) PO x S U^ETOM PRAWILA DIFFERENCIROWANIQ SLOVNOJ FUNKCII, POLU^AEM 2x + 2yy0 = 0. oTS@DA PRI y 6= 0 NAJDEM y0 = −x/y. tAKIM OBRAZOM, W DANNOM SLU^AE UDALOSX NAJTI PROIZWODNU@ y0, NE USTANAWLIWAQ QWNOJ ZAWISIMOSTI y OT x.

dIFFERENCIAL (1) ESTX 2xdx + 2ydy = 0, A ZNA^IT, dy = −(x/y)dx. dIFFERENCIRUQ RAWENSTWO y0 = −x/y E]E RAZ I U^ITYWAQ WYRAVENIE DLQ PER-

WOJ PROIZWODNOJ I (1), ZAPISYWAEM

fUNKCI@ y = f(x) NAZYWA@T PARAMETRI^ESKI ZADANNOJ SOOTNO[ENIQMI (2),

FUNKCII WOZNIKA@T PRI RASSMOTRENII KRIWYH NA PLOSKOSTI

NO, NA KOORDINATNOJ PLOSKOST xOy L@BOMU ZNA^ENI@ PARAMETRA t IZ PROMEVUTKA (a, b) SOOTWETSTWUET TO^KA S KOORDINATAM (x; y). pRI IZMENENII t TO^KA OPISYWAET NEKOTORU@ KRIWU@, A (2) QWLQ@TSQ PARAMETRI^ESKIMI URAWNENIQMI \TOJ

KRIWOJ.

eSLI FUNKCIQ x = x(t) IMEET PRI t (a, b) OBRATNU@ FUNKCI@ t = t(x), TO

^ASTI, NA KOTORYH FUNKCIQ x = x(t) STROGO MONOTONNA, NA KAVDOM TAKOM U^ASTKE OT PARAMETRI^ESKI ZADANNOJ FUNKCII MY MOVEM PEREJTI K ANALITI^ESKI ZADANNOJ FUNKCII y = f(x). oDNAKO OBRATNAQ FUNKCIQ \LEMENTARNOJ FUNKCII NE WSEGDA

QWLQETSQ \LEMENTARNOJ. pO\TOMU PEREHOD OT PARAMETRI^ESKOGO SPOSOBA ZADANIQ FUNKCII K QWNOMU ANALITI^ESKOMU NE WSEGDA WOZMOVEN W KLASSE \LEMENTARNYH FUNKCIJ.

pRIMER 2. cIKLOIDA — TRAEKTORIQ TO^KI, LEVA]EJ NA KOLESE, ESLI KOLESO KATITSQ BEZ SKOLXVENIQ PO PRQMOJ.

zADA^A 1. dOKAVITE, ^TO CIKLOIDA ZADAETSQ URAWNENIQMI

x = a(t − sin t), y = a(1 − cos t).

oTMETIM, ^TO FUNKCIQ x = a(t − sin t) QWLQETSQ WOZRASTA@]EJ NA WSEJ PRQMOJ R. pO\TOMU CIKLOIDA QWLQETSQ GRAFIKOM NEKOTOROJ FUNKCII , NO \TA FUNKCIQ

66

NE QWLQETSQ \LEMENTARNOJ, TAK KAK PARAMETR t NE UDAETSQ ISKL@^ITX IZ DANNYH URAWNENIJ I QWNO WYRAZITX y ^EREZ x W KLASSE \LEMENTARNYH FUNKCIJ. .

sLEDU@]AQ TEOREMA POZWOLQET WY^ISLQTX PROIZWODNU@ PARAMETRI^ESKI ZADAN - NOJ FUNKCII, NE NAHODQ EE QWNOGO PREDSTAWLENIQ. pRI \TOM PROIZWODNAQ PARAME- TRI^ESKI ZADANNOJ FUNKCII QWLQETSQ PARAMETRI^ESKI ZADANNOJ FUNKCIEJ .

tEOREMA 2 (PROIZWODNAQ PARAMETRI^ESKI ZADANNOJ FUNKCII).

pUSTX W (2) FUNKCII x(t) I y(t) DIFFERENCIRUEMY W PROMEVUTKE T , PRI^EM x0(t) 6= 0 DLQ WSEH t T , I FUNKCIQ x(t) STROGO MONOTONNA W \TOM PROMEVUTKE. tOGDA PRO- IZWODNAQ FUNKCII, ZADANNOJ PARAMETRI^ESKI SOOTNO[ENIQMI (2), QWLQETSQ FUNK- CIEJ, PARAMETRI^ESKI ZADANNOJ SOOTNO[ENIQMI

dOK–WO. pO TEOREME O SU]ESTWOWANII I NEPRERYWNOSTI OBRATNOJ FUNKCII SU]E - STWUET FUNKCIQ t = t(x), OPREDELENNAQ I NEPRERYWNAQ W PROMEVUTKE X = x(T ), OBRATNAQ K FUNKCII x(t). sOGLASNO TEOREME O PROIZWODNOJ OBRATNOJ FUNKCII \TA

FUNKCIQ DIFFERENCIRUEMA W X. pO\TOMU SLOVNAQ FUNKCIQ y = f(x) = y t(x) = (y ◦ t)(x) OPREDELENA W PROMEVUTKE X I UDOWLETWORQET USLOWIQM TEOREMY O PROIZ - WODNOJ SLOVNOJ FUNKCII. iSPOLXZUQ \TU TEOREMU WMESTE S TEOREMOJ O PROIZWODNOJ OBRATNOJ FUNKCII, POLU^AEM yx0 = y0(t)t0(x) = y0(t)/x0(t) t T . .

zAME^ANIQ. 1. dLQ LU^[EGO ZAPOMINANIQ FORMULY IZ TEOREMY 2 EE LU^[E ZAPISATX W WIDE:

dy

dxdy = dxdt .

dt

2. dLQ WY^ISLENIQ WTOROJ PROIZWODNOJ PARAMETRI^ESKI ZADANNOJ FUNKCII SLEDU - ET DWAVDY PRIMENITX TEOREMU 2, PRI \TOM W OB]EM SLU^AE

3. dLQ WY^ISLENIQ DIFFERENCIALA PARAMETRI^ESKI ZADANNOJ FUNKCII MOVNO WY - ^ISLITX DIFFERENCIALY y I x KAK FUNKCIJ t I, ISKL@^IW IZ DANNYH URAWNENIJ dt, QWNO WYRAZITX dy ^EREZ dx.

pRIMER 2. nAJDEM y0, dy, y00 W SLU^AE CIKLOIDY. fUNKCIQ x = a(t −sin t) QWLQ- ETSQ WOZRASTA@]EJ NA WSEM MNOVESTWE R DEJSTWITELXNYH ^ISEL. iMEEM

I PO TEOREME 2

67

e]E RAZ PRIMENQQ TEOREMU 2, NO UVE K FUNKCII (3), POLU^AEM

pRI WY^ISLENII DIFFERENCIALA SNA^ALA POLU^AEM dx = a(1 − cos t)dt I dy = a sin tdt, A ZATEM

dy = 1 − cos tdt.

22 oSNOWNYE TEOREMY DIFFERENCIALXNOGO IS^I - SLENIQ

sM. [iW: §5.1–5.3, STR. 106–123].

|TI TEOREMY DA@T INFORMACI@ O ZNA^ENII PROIZWODNOJ FUNKCII W NEKOTOROJ WNUTRENNEJ TO^KE RASSMATRIWAEMOGO OTREZKA .

22.1tEOREMY O NULQH PROIZWODNYH

tO^KU x0 E R NAZYWA@T TO^KOJ LOKALXNOGO MINIMUMA FUNKCII f : E →

R, A ZNA^ENIE FUNKCII W NEJ — LOKALXNYM MINIMUMOM, ESLI

1)TO^KA x0 QWLQETSQ PREDELXNOJ DLQ LEWOJ E ∩ (−∞; x0) I PRAWOJ E ∩ (x0; +∞) ^ASTEJ OBLASTI OPREDELENIQ FUNKCII,

2)SU]ESTWUET WYKOLOTAQ OKRESTNOSTX U˙ (x0) TO^KI x0 TAKAQ, ^TO W L@BOJ TO^KE

x U˙ (x0) ∩ E IMEEM f(x0) 6 f(x).

aNALOGI^NO (IZMENQQ TOLXKO TIP NERAWENSTWA) OPREDELQ@TSQ TO^KI LOKALX-

NOGO MAKSIMUMA (f(x0) > f(x)), STROGOGO LOKALXNOGO MINIMUMA (f(x0) < f(x)) I STROGOGO LOKALXNOGO MAKSIMUMA (f(x0) > f(x)).

lOKALXNYJ MAKSIMUM ILI LOKALXNYJ MINIMUM NAZYWA@T LOKALXNYM \KS- TREMUMOM, A STROGIE LOKALXNYE MAKSIMUM ILI MINIMUM — STROGIM LOKALX-

NYM \KSTREMUMOM.

pRIMER 1. nA RIS. 29 SPLO[NOJ LINIEJ IZOBRAVEN GRAFIK FUNKCII f(x), OPRE-

DELENNOJ NA OTREZKE [a, b]. w DANNOM SLU^AE TO^KI x , d I x1 — TO^KI LOKALXNOGO MAKSIMUMA, c I x2 — TO^KI LOKALXNOGO MINIMUMA, WSE x (c, d) — TO^KI LOKALX- NOGO \KSTREMUMA (LOKALXNYH MAKSIMUMA I MINIMUMA ODNOWREMENNO). fUNKCIQ NE

OPREDELENA SLEWA OT TO^KI a I SPRAWA OT TO^KI b, PO\TOMU TO^KI a I b NE QWLQ@TSQ TO^KAMI LOKALXNOGO \KSTREMUMA.

rIS. 29

68

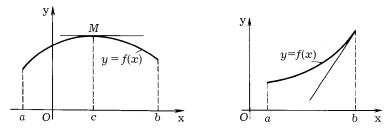
dALEE SLOWA ”STROGIJ” I ”LOKALXNYJ” BUDEM INOGDA OPUSKATX. pRI \TOM TO^KU x0 BUDEM NAZYWATX TO^KOJ \KSTREMUMA (MAKSIMUMA ILI MINIMUMA), A ZNA^E- NIE f(x0) FUNKCII — \KSTREMALXNYM (MAKSIMALXNYM ILI MINIMALXNYM). eSLI W TO^KE f(x) DOSTIGAET MAKSIMUMA ILI MINIMUMA, TO BUDEM PI- SATX SOOTWETSTWENNO f(x0) = fmax ILI f(x0) = fmin. tAKIM OBRAZOM, NA RIS. 29 x , d, x1 I x2 — TO^KI \KSTREMUMA FUNKCII f(x) (x , d I x1 — TO^KI MAKSIMUMA I x2 — TO^KA MINIMUMA). sLEDUET ZAMETITX, ^TO MAKSIMALXNOE ZNA^ENIE FUNKCII f(x) W INTERWALE (a, b) NE OBQZANO BYTX BOLX[E L@BOGO MINIMALXNOGO ZNA^ENIQ \TOJ FUNK - CII W DANNOM INTERWALE. nAPRIMER, MAKSIMALXNOE ZNA^ENIE f(x ) FUNKCII f(x), GRAFIK KOTOROJ IZOBRAVEN NA RIS. 29, MENX[E EE MINIMALXNOGO ZNA^ENIQ f(x2). oDNAKO ESLI c E R — TO^KA (GLOBALXNOGO) \KSTREMUMA FUNKCII f : E → R NA OBLASTI OPREDELENIQ FUNKCII I TO^KA c QWLQETSQ PREDELXNOJ DLQ E ∩ (−∞; x0) I DLQ E ∩ (x0; +∞), TO x0 — TO^KA LOKALXNOGO \KSTREMUMA \TOJ FUNKCII.

tEOREMA 1 (fERMA). eSLI FUNKCIQ y = f(x) IMEET KONE^NU@ PROIZWODNU@ W TO^KE LOKALXNOGO \KSTREMUMA c, TO f0(c) = 0.

dOK–WO. pO OPREDELENI@ W TO^KE c LOKALXNOGO MINIMUMA PRI MALYH x IMEEM

f(c) = f(c + x) − f(c) > 0. pO TEOREME O PREDELXNOM PEREHODE W NERAWENSTWE POLU^AEM

a ZNA^IT, f0(c) = 0. aNALOGI^NO W TO^KE LOKALXNOGO MAKSIMUMA. .

gEOMETRI^ESKIJ SMYSL TEOREMY. oBRA]ENIE W NULX PROIZWODNOJ f0(c)

OZNA^AET, ^TO KASATELXNAQ K KRIWOJ GRAFIKA FUNKCII f(x) W TO^KE M(c; f(c)) PA- RALLELXNA OSI Ox (RIS. 30).

pRI DOKAZATELXSTWE TEOREMY fERMA SU]ESTWENNO ISPOLXZOWANIE TOGO , ^TO c QWLQETSQ PREDELXNOJ DLQ LEWOJ I PRAWOJ ^ASTEJ OBLASTI OPREDELENIQ FUNKCII . |TO POZWOLILO RASSMATRIWATX TO^KI x, LEVA]IE KAK SPRAWA, TAK I SLEWA OT TO^KI c. bEZ \TOGO PREDPOLOVENIQ UTWERVDENIE TEOREMY MOVET OKAZATXSQ NEWERNYM . w SAMOM DELE, ESLI FUNKCIQ DOSTIGAET NAIBOLX[EGO ZNA^ENIQ W GRANI^NOJ TO^KE NA ODNOM IZ KONCOW (a ILI b) PROMEVUTKA, TO PROIZWODNAQ W TAKOJ TO^KE (PRI USLOWII, ^TO PROIZWODNAQ SU]ESTWUET) MOVET I NE BYTX RAWNOJ NUL@ (RIS. 31).

1)NEPRERYWNA NA OTREZKE [a, b];

2)DIFFERENCIRUEMA W INTERWALE (a, b);

3)NA KONCAH OTREZKA PRINIMAET RAWNYE ZNA^ENIQ (f(a) = f(b)),

69

TO MEVDU TO^KAMI a I b NAJDETSQ, PO KRAJNEJ MERE, ODNA TO^KA c (a < c < b), W KOTOROJ f0(c) = 0.

dOK–WO. tAK KAK FUNKCIQ y = f(x) NEPRERYWNA NA OTREZKE [a, b], ONA, SOGLASNO TEOREME wEJER[TRASSA, DOSTIGAET NA \TOM OTREZKE SWOIH NAIBOLX[EGO M I NAI- MENX[EGO m ZNA^ENIJ. rASSMOTRIM DWA SLU^AQ.

1. M = m. fUNKCIQ f(x) W INTERWALE (a, b) SOHRANQET POSTOQNNOE ZNA^ENIE, I PO\TOMU f0(x) = 0 x (a, b), T.E. W KA^ESTWE c MOVNO WZQTX L@BU@ TO^KU IZ INTERWALA (a, b).

2. M > m. pOSKOLXKU, SOGLASNO USLOWI@ TEOREMY, f(a) = f(b), ODNOGO IZ ZNA- ^ENIJ M ILI m FUNKCIQ DOSTIGAET WO WNUTRENNEJ TO^KE c INTERWALA (a, b). tOGDA IZ TEOREMY fERMA SLEDUET, ^TO W \TOJ TO^KE f0(c) = 0. .

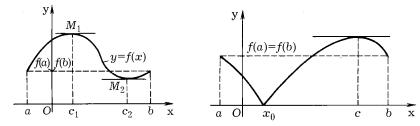
tEOREMA rOLLQ IMEET SLEDU@]EE GEOMETRI^ESKOE TOLKOWANIE: ESLI ORDI- NATY NEPRERYWNOJ KRIWOJ NA KONCAH OTREZKA [a, b] RAWNY MEVDU SOBOJ I KRIWAQ W KAVDOJ WNUTRENNEJ TO^KE \TOGO OTREZKA IMEET NEWERTIKALXNU@ KASATELXNU@ , TO NA KRIWOJ NAJDETSQ HOTQ BY ODNA TO^KA, W KOTOROJ KASATELXNAQ PARALLELXNA OSI Ox (NA RIS. 32 TO^KI M1 I M2, SOOTWETSTWU@]IE TO^KAM c1 I c2 INTERWALA (a, b) ).

rIS. 32 rIS. 33

zAMETIM, ^TO WSE USLOWIQ TEOREMY rOLLQ SU]ESTWENNY DLQ SPRAWEDLIWOSTI EE UTWERVDENIQ. nAPRIMER, FUNKCIQ y = |x| NEPRERYWNA NA OTREZKE [−1, 1], PRINIMA- ET NA EGO KONCAH RAWNYE ZNA^ENIQ, NO NE IMEET KONE^NOJ DWUSTORONNEJ PROIZWODNOJ W TO^KE x = 0, WNUTRENNEJ DLQ \TOGO OTREZKA. tAK KAK y0 = +1 x (0, 1) I y0 = −1x (−1, 0), W INTERWALE (−1, 1) NET NI ODNOJ TO^KI, W KOTOROJ BY PROIZWODNAQ y0 OBRA]ALASX W NULX.

oDNAKO TEOREMA rOLLQ NOSIT LI[X DOSTATO^NYJ HARAKTER , T.E. ESLI WSE USLOWIQ TEOREMY WYPOLNENY, TO EE UTWERVDENIE WERNO, NO ESLI NARU[ENO HOTQ BY ODNO EE USLOWIE, TO NELXZQ SKAZATX ^TO-LIBO OPREDELENNOE O SU]ESTWOWANII TO^KI, W KOTOROJ PROIZWODNAQ RASSMATRIWAEMOJ FUNKCII OBRA]ALASX BY W NULX . nA RIS. 33 WIDNO, ^TO FUNKCIQ f(x) NEPRERYWNA NA OTREZKE [a, b], NA KONCAH OTREZKA IMEET

RAWNYE ZNA^ENIQ, NO NE QWLQETSQ DIFFERENCIRUEMOJ WO WNUTRENNEJ TO^KE x0 \TOGO OTREZKA. tEM NE MENEE SU]ESTWUET TO^KA x = c, W KOTOROJ f0(c) = 0 (KASATELXNAQ W

SOOTWETSTWU@]EJ TO^KE KRIWOJ GRAFIKA \TOJ FUNKCII PARALLELXNA OSI Ox). eSLI FUNKCIQ s = f(t) ZADAET ZAWISIMOSTX OT WREMENI t KOORDINATY s TO^KI

PRI EE NEPRERYWNOM PRQMOLINEJNOM DWIVENII, TO USLOWIE f(a) = f(b) OZNA^AET, ^TO \TA TO^KA POSLE NA^ALA DWIVENIQ W MOMENT WREMENI a ^EREZ PROMEVUTOK WRE- MENI b−a DOLVNA WERNUTXSQ W ISHODNOE POLOVENIE . nO DLQ \TOGO HOTQ BY W ODIN IZ PROMEVUTO^NYH MOMENTOW WREMENI t0 (a, b) EE SKOROSTX DWIVENIQ f0(t0) DOLVNA STATX RAWNOJ NUL@. tAKOWA MEHANI^ESKAQ INTERPRETACIQ TEOREMY rOLLQ.

70