MAiu9

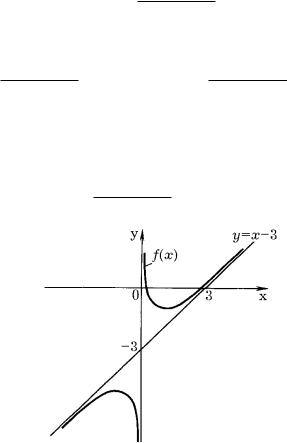
PRI^EM POSLEDNIE DWA WIDA MOGUT BYTX KAK ODNOSTORONNIMI, PRAWYMI PRI x → +∞ ILI LEWYMI PRI x → −∞, TAK I DWUSTORONNIMI PRI x → ∞, T.E.

I PRAWYM, I LEWYMI ODNOWREMENNO. dALEE BUDEM S^ITATX, ^TO GORIZONTALXNYE ASIMPTOTY — \TO ^ASTNYJ SLU^AJ NAKLONNYH (PRI k = 0).

tEOREMA 1. pRQMAQ {x = a} QWLQETSQ WERTIKALXNOJ ASIMPTOTOJ GRAFIKA FUNK -

CII y = f(x) f(a + 0) = ±∞ ILI f(a − 0) = ±∞.

dOK–WO SLEDUET IZ OPREDELENIJ.

w SLU^AE LEWOJ NAKLONNOJ ASIMPTOTY FORMULIROWKA ANALOGI^NA , TOLXKO W OBO- IH PREDELAH x → −∞.

dOK–WO. iZ OPREDELENIQ SLEDUET: y = kx + b — URAWNENIE PRAWOJ NAKLONNOJ ASIMPTOTY α(x) = f(x) − kx − b — B.M. PRI x → +∞.

oTS@DA SLEDU@T UTWERVDENIE ” ” TEOREMY.

oBRATNO, IZ WTOROGO PREDELA I TEOREMY O SWQZI FUNKCII , EE PREDELA I BESKO- NE^NO MALOJ SLEDUET, ^TO α(x) = f(x) − kx − b — B.M., A ZNA^IT, {y = kx + b} — ASIMPTOTA. .

pRIMER 2. nAJDEM WERTIKALXNYE I NAKLONNYE ASIMPTOTY GRAFIKA FUNKCII

f(x) = x2 − 3x + 1. x

fUNKCIQ OPREDELENA PRI x R \ {0}. wY^ISLIM PREDELY

CLEDOWATELXNO, PRQMAQ x = 0 — WERTIKALXNAQ ASIMPTOTA GRAFIKA RASSMATRIWAE -

MOJ FUNKCII.

dLQ NAHOVDENIQ NAKLONNYH ASIMPTOT GRAFIKA PREDSTAWIM \TU FUNKCI@ W WIDE

rIS. 39

81

tAK KAK 1/x → 0 PRI x → ∞, TO IZ OPREDELENIQ NAKLONNOJ ASIMPTOTY SLEDUET , ^TO PRQMAQ y = x−3 QWLQETSQ DWUSTORONNEJ NAKLONNOJ ASIMPTOTOJ GRAFIKA UKAZANNOJ FUNKCII. pOSKOLXKU 1/x > 0 PRI x > 0 I 1/x < 0 PRI x < 0, KRIWAQ GRAFIKA LEVIT WY[E ASIMPTOTY PRI x → +∞ I NIVE EE PRI x → −∞ (RIS. 39).

25.2uSLOWIQ WOZRASTANIQ I UBYWANIQ FUNKCIJ

wYQSNIM TEPERX, KAK PO PROIZWODNOJ FUNKCII MOVNO SUDITX O WOZRASTANII (ILI UBYWANII) SAMOJ FUNKCII NA PROMEVUTKE. nAPOMNIM, ^TO FUNKCI@ f(x) NAZY- WA@T WOZRASTA@]EJ (UBYWA@]EJ) W INTERWALE (a, b), ESLI BOLX[EMU ZNA^ENI@ EE ARGUMENTA x W \TOM INTERWALE SOOTWETSTWUET BOLX[EE (MENX[EE) ZNA^ENIE FUNK- CII, T.E.

fUNKCI@ NAZYWA@T NEUBYWA@]EJ (NEWOZRASTA@]EJ) W INTERWALE (a, b), ESLI BOLX- [EMU ZNA^ENI@ ARGUMENTA W \TOM INTERWALE SOOTWETSTWUET NE MENX[EE (NE BOLX- [EE) ZNA^ENIE FUNKCII:

pRI \TOM W PERWOM SLU^AE FUNKCI@ IMENU@T STROGO MONOTONNOJ , A WO WTOROM — MONOTONNOJ.

tEOREMA 3 (KRITERIJ MONOTONNOSTI FUNKCII). dIFFERENCIRUEMAQ NA

0x (a, b).

dOK–WO DLQ NEUBYWA@]EJ FUNKCII.

: I DLQ x > 0, I DLQ x < 0 IMEEM f(x+Δx)−f(x) > 0. oTS@DA PRI x → 0 PO TEOREME O PREDELXNOM PEREHODE W NERAWENSTWE POLU^AEM f0(x) > 0.

: DLQ PROIZWOLXNYH x1, x2 (a; b) TAKIH, ^TO x1 < x2, PO TEOREME lAGRANVA

c (x1, x2) f(x2) − f(x1) = f0(c)(x2 − x1) > 0,

T.E. f — NEUBYWA@]AQ FUNKCIQ NA INTERWALE (a, b). aNALOGI^NO DLQ NEWOZRASTA@]EJ FUNKCII. .

tEOREMA 4 (DOSTATO^NOE USLOWIE STROGOJ MONOTONNOSTI FUNKCII). 1) eSLI DLQ DIFFERENCIRUEMOJ W INTERWALE (a, b) FUNKCII f(x)

WOZRASTAET (UBYWAET) NA \TOM INTERWALE.

f(x) NEPRERYWNA NA OTREZKE [a, b], TO ONA WOZRASTAET

dOK–WO ANALOGI^NO PREDYDU]EMU: 1) PO TEOREME lAGRANVA

x1, x2 (a; b) (x1 < x2) c (x1, x2) : f(x2) − f(x1) = f0(c)(x2 − x1) > 0,

A ZNA^IT, f — WOZRASTA@]AQ FUNKCIQ NA INTERWALE (a, b).

2) eSLI f NEPRERYWNA NA OTREZKE [a, b], TO W KA^ESTWE x1, x2 W PREDYDU]EM RASSUVDENII MOVNO WZQTX PROIZWOLXNYE TO^KI IZ OTREZKA [a; b].

82

aNALOGI^NO DLQ UBYWA@]EJ FUNKCII. .

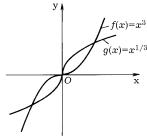
pRIMER 3. dOSTATO^NOE USLOWIE STROGOJ MONOTONNOSTI DLQ FUNKCIJ

x3 I g(x) = x1/3 NA L@BOM INTERWALE, SODERVA]EM 0, NE WYPOLNQETSQ, TAK KAK f0(0) = 0, A g0(0) = ∞, HOTQ \TI FUNKCII WOZRASTA@T NA WSEJ ^ISLOWOJ PRQMOJ (RIS. 40). pO\TOMU DOSTATO^NOE USLOWIE STROGOJ MONOTONNOSTI IZ TEOREMY 4 NE QWLQETSQ NEOBHODIMYM.

rIS. 40

nEOBHODIMOE I DOSTATO^NOE USLOWIE MONOTONNOSTI QWLQETSQ I NEOBHODIMYM USLOWIEM STROGOJ MONOTONNOSTI.

dOKAZANNYE TEOREMY IME@T SLEDU@]IJ GEOMETRI^ESKIJ SMYSL: ESLI W IN- TERWALE (a, b) FUNKCIQ f(x) WOZRASTAET, TO KASATELXNAQ K KRIWOJ y = f(x) W KONE^- NOM ^ISLE TO^EK MOVET BYTX GORIZONTALXNA ILI WERTIKALXNA , A DLQ WSEH OSTALX- NYH TO^EK x (a, b) OBRAZUET OSTRYJ UGOL S OSX@ Ox. tAK, NAPRIMER, FUNKCII IZ PRIMERA 3 WOZRASTA@T NA WSEJ PRQMOJ, NO KASATELXNAQ W TO^KE x = 0 ODNOJ IZ NIH GORIZONTALXNA, A WTOROJ — WERTIKALXNA. eSLI VE FUNKCIQ f(x) UBYWAET W INTER- WALE (a, b), TO KASATELXNAQ K KRIWOJ y = f(x) DLQ WSEH x (a, b) OBRAZUET TUPOJ UGOL S OSX@ Ox (W KONE^NOM ^ISLE TO^EK KASATELXNAQ MOVET BYTX GORIZONTALXNA ILI WERTIKALXNA).

25.3mAKSIMUM I MINIMUM FUNKCII

oPREDELENIQ I PRIMERY TO^EK (STROGOGO) LOKALXNOGO \KSTREMUMA, MAKSIMUMA I MINIMUMA, ZNA^ENIJ FUNKCII \KSTREMALXNOGO, MAKSIMALXNOGO I MINIMALXNOGO, A TAKVE TEOREMA fERMA BYLI PRIWEDENY W P. 22.1.

LOKALXNOGO MINIMUMA DANNYH FUNKCIJ PRI \TOM FUNKCIQ IZ PRIMERA 4 IMEET NULEWU@ PROIZWODNU@, A FUNKCIQ IZ PRIMERA 5 NE IMEET PROIZWODNU@ W \TOJ TO^KE.

tO^KI, W KOTORYH PROIZWODNAQ FUNKCII f(x) RAWNA NUL@, NAZYWA@T STACIO- NARNYMI TO^KAMI \TOJ FUNKCII. tO^KI, W KOTORYH PROIZWODNAQ FUNKCII f(x) RAWNA NUL@, BESKONE^NA ILI NE SU]ESTWUET NAZYWA@T KRITI^ESKIMI TO^KAMI

(I PORQDKA) FUNKCII f(x).

tEOREMA 5 (NEOBHODIMOE USLOWIE \KSTREMUMA).

eSLI x0 — TO^KA LOKALXNOGO \KSTREMUMA FUNKCIII, TO x0 — KRITI^ESKAQ TO^KA I PORQDKA \TOJ FUNKCII.

dOK–WO SLEDUET IZ TEOREMY fERMA.

eSLI \KSTREMUM FUNKCII DOSTIGAETSQ W TO^KE, GDE PROIZWODNAQ BESKONE^NA ILI NE SU]ESTWUET, TO EGO ^ASTO NAZYWA@T OSTRYM \KSTREMUMOM (SM. PRIMER 5) W

83

OTLI^IE OT GLADKOGO \KSTREMUMA, KOTORYJ DOSTIGAETSQ W STACIONARNOJ TO^KE FUNKCII (SM. PRIMER 4).

pRIMER 6. tO^KA x = 0 QWLQETSQ KRITI^ESKOJ TO^KOJ FUNKCIJ f(x) = x3 I g(x) = x1/3, NO NE QWLQETSQ TO^KOJ LOKALXNOGO \KSTREMUMA \TIH FUNKCIJ (RIS. 40). tAKIM OBRAZOM, TEOREMA 3 NE DAET DOSTATO^NOGO USLOWIQ.

tEOREMA 6 (PERWYJ DOSTATO^NYJ PRIZNAK \KSTREMUMA).

pUSTX FUNKCIQ y = f(x) NEPRERYWNA W NEKOTOROJ OKRESTNOSTI KRITI^ESKOJ TO^KI

x0 I DIFFERENCIRUEMA WO WSEH TO^KAH SOOTWETSTWU@]EJ WYKOLOTOJ OKRESTNOSTI . eSLI PRI PEREHODE ARGUMENTA x SLEWA NAPRAWO ^EREZ \TU TO^KU PROIZWODNAQ f0(x)

MENQET ZNAK, TO W TO^KE x0 FUNKCIQ f(x) IMEET \KSTREMUM, PRI^EM ESLI PROIZWOD- NAQ MENQET ZNAK S MINUSA NA PL@S, TO x0 — TO^KA LOKALXNOGO MINIMUMA, ESLI VE S

PL@SA NA MINUS, TO x0 — TO^KA LOKALXNOGO MAKSIMUMA. eSLI I SLEWA, I SPRAWA OT TO^KI x0 W NEKOTOROJ WYKOLOTOJ OKRESTNOSTI \TOJ TO^KI PROIZWODNAQ f0(x) IMEET

ODIN ZNAK, TO TO^KA x0 NE QWLQETSQ TO^KOJ LOKALXNOGO \KSTREMUMA FUNKCII f(x).

dOK–WO SLEDUET IZ DOSTATO^NOGO USLOWIQ STROGOJ MONOTONNOSTI FUNKCII NA OTREZKAH [x1; x0] I [x0; x2], GDE TO^KI x1 I x2 WYBRANY TAK, ^TO DANNYE OTREZKI LEVAT W UKAZANNOJ W USLOWII OKRESTNOSTI .

zADA^A 1. dAJTE GEOMETRI^ESKU@ ILL@STRACIQ DANNOJ TEOREMY DLQ WSEH RASSMATRIWAEMYH SLU^AEW.

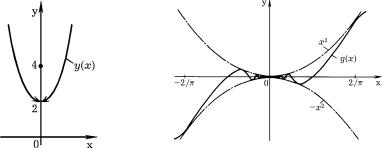
PROIZWODNAQ y0 = 6x SU]ESTWUET WO WSEH TO^KAH, KROME x = 0, I MENQET ZNAK S MINUSA NA PL@S PRI PEREHODE ^EREZ TO^KU x = 0. tEM NE MENEE \TA FUNKCIQ IMEET W TO^KE x = 0 NE MINIMUM, A MAKSIMUM, ^TO NETRUDNO PROWERITX NEPOSREDSTWENNO (RIS. 41). dELO W TOM, ^TO TEOREMA 6 NE PRIMENIMA W DANNOM SLU^AE, TAK KAK FUNKCIQ TERPIT RAZRYW W TO^KE x = 0. .

tAKIM OBRAZOM, USTANOWLENNOE W TEOREME 6 DOSTATO^NOE USLOWIE SU]ESTWOWANIQ \KSTREMUMA NELXZQ ISPOLXZOWATX, ESLI FUNKCIQ NE QWLQETSQ NEPRERYWNOJ W KRI-

TI^ESKOJ TO^KE. oNO NE PRIMENIMO I TOGDA, KOGDA L@BAQ WYKOLOTAQ OKRESTNOSTX RASSMATRIWAEMOJ KRITI^ESKOJ TO^KI FUNKCII SODERVIT BESKONE^NOE MNOVESTWO DRUGIH EE KRITI^ESKIH TO^EK, A PROIZWODNAQ \TOJ FUNKCII NE SOHRANQET OPREDE -

LENNOGO ZNAKA W L@BOJ POLUOKRESTNOSTI RASSMATRIWAEMOJ TO^KI .

84

PREDSTAWLEN NA RIS. 42. sOSTAWIM DLQ \TOJ FUNKCII RAZNOSTNOE OTNO[ENIE W TO^KE

x = 0:

pOSKOLXKU PRI x → 0 f(0)/ x → 0, IZ OPREDELENIQ PROIZWODNOJ SLEDUET, ^TO f0(0) = 0. oDNAKO W L@BOJ SKOLX UGODNO MALOJ OKRESTNOSTI STACIONARNOJ TO^KI x = 0 PROIZWODNAQ

f0(x) = 2x sin x1 − cos x1

RASSMATRIWAEMOJ FUNKCII BESKONE^NOE ^ISLO RAZ MENQET ZNAK . pO\TOMU W DANNOM SLU^AE TEOREMU 6 NELXZQ ISPOLXZOWATX.

pO TOJ VE PRI^INE NE PRIMENIMA TEOREMA 6 I K FUNKCII

rAZLI^IE MEVDU \TIMI FUNKCIQMI SOSTOIT W TOM, ^TO DLQ WTOROJ IZ NIH IMEEM g(x) > x2 > 0 = g(0), I, SOGLASNO OPREDELENI@, W TO^KE x = 0 ONA IMEET MINIMUM. a DLQ PERWOJ IZ NIH NELXZQ UKAZATX TAKOJ WYKOLOTOJ OKRESTNOSTI , W KOTOROJ BYLO BY LIBO f(0) = 0 < f(x), LIBO f(0) = 0 > f(x) (FUNKCIQ NE^ETNAQ I NE QWLQETSQ KONSTANTOJ), T.E. PERWAQ IZ FUNKCIJ \KSTREMUMA W TO^KE x = 0 NE IMEET. .

w SLU^AQH, KOGDA TEOREMA 6 NE PRIMENIMA, NUVNY DOPOLNITELXNYE ISSLEDOWANIQ.

25.4iSSLEDOWANIE FUNKCIJ NA \KSTREMUM S POMO]X@ WYS -

[IH PROIZWODNYH

tEOREMA 7 (WTOROJ DOSTATO^NYJ PRIZNAK \KSTREMUMA). pUSTX FUNKCIQ

y = f(x) DIFFERENCIRUEMA W NEKOTOROJ OKRESTNOSTI TO^KI x0, f0(x0) = 0, A f00(x0) SU]ESTWUET, KONE^NA I NE RAWNA NUL@. tOGDA PRI f00(x0) < 0 x0 — TO^KA LOKALXNOGO MAKSIMUMA, A PRI f00(x0) > 0 x0 — TO^KA LOKALXNOGO MINIMUMA.

dOK–WO DLQ SLU^AQ f00(x0) < 0. iZ TEOREMY O SOHRANENII ZNAKA SLEDUET:

t.E. ZNAK MENQETSQ S + NA -. pO TEOREME 6 POLU^AEM NA[E UTWERVDENIE. sLU^AJ f00(x0) > 0 RASSMATRIWAETSQ ANALOGI^NO. .

pRIMER 9. y = x − 2 ln x.

tEOREMA 8 (TRETIJ DOSTATO^NYJ PRIZNAK \KSTREMUMA). pUSTX FUNKCIQ f(x) IMEET W OKRESTNOSTI TO^KI x0 PROIZWODNYE DO PORQDKA n − 1 I PROIZWODNU@

85

PORQDKA n W TO^KE x0, PRI^EM WSE EE PROIZWODNYE DO (n−1)-GO PORQDKA WKL@^ITELX- NO W \TOJ TO^KE RAWNY NUL@: f0(x0) = f00(x0) = . . . = f(n−1)(x0) = 0, A f(n)(x0) 6= 0.

tOGDA,

1)ESLI n ^ETNOE, TO W TO^KE x0 FUNKCIQ IMEET \KSTREMUM, PRI^EM PRI f(n)(x0) < 0 x0 — TO^KA LOKALXNOGO MAKSIMUMA,

A PRI f(n)(x0) > 0 x0 — TO^KA LOKALXNOGO MINIMUMA.

2)eSLI n NE^ETNOE, TO x0 NE QWLQETSQ TO^KOJ LOKALXNOGO \KSTREMUMA DANNOJ FUNK - CII.

dOK–WO: FORMULA tEJLORA PORQDKA n DLQ FUNKCII f(x) W TO^KE x0 IMEET WID

PRI f(n)(x0) > 0 f(x) > f(x0) I, PO OPREDELENI@, x0 — TO^KA LOKALXNOGO MINIMUMA. dLQ NE^ETNOGO n SOMNOVITELX (x−x0)n MENQET ZNAK PRI PEREHODE ARGUMENTA x ^EREZ ZNA^ENIE x0, A SOMNOVITELX f(n)(x0) NET. sLEDOWATELXNO, RAZNOSTX f(x) − f(x0)

TAKVE MENQET ZNAK, I PO\TOMU TO^KA x0 NE QWLQETSQ TO^KOJ \KSTREMUMA FUNKCII

f(x). .

pRIMER 10. y = x2 + cos x. 2

26 uSLOWIQ WYPUKLOSTI FUNKCII

sM. [iW: §8.4 STR. 207–213] ILI [z: STR. 238–241].

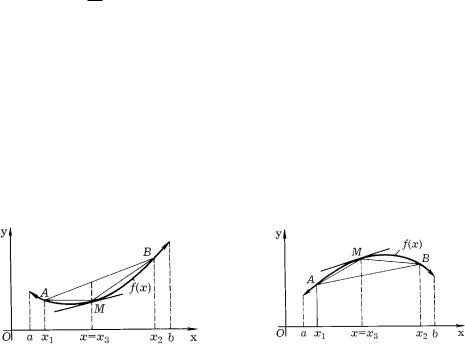
fUNKCI@ f(x), OPREDELENNU@ NA INTERWALE (a, b), NAZYWA@T WYPUKLOJ WNIZ W \TOM INTERWALE, ESLI L@BAQ DUGA EE GRAFIKA LEVIT NE WY[E STQGIWA@]EJ \TU

DUGU HORDY (RIS. 43). dLQ OPREDELENIQ WYPUKLYH WWERH (RIS. 44), STROGO WY- PUKLYH WNIZ I STROGO WYPUKLYH WWERH FUNKCIJ DOSTATO^NO W PRIWEDENNOM OPREDELENII SLOWOSO^ETANIE ”NE WY[E” ZAMENITX SOOTWETSTWENNO NA ”NE NIVE”,

”NIVE” I ”WY[E”.

sU]ESTWU@T FUNKCII, KOTORYE WYPUKLYE WNIZ I WWERH ODNOWREMENNO , \TO LI- NEJNYE NA INTERWALE FUNKCII. dEJSTWITELXNO, DUGA GRAFIKA TAKOJ FUNKCII LE- VIT NE WY[E I NE NIVE HORDY, A ZNA^IT, SOWPADAET S NEJ, T.E. QWLQETSQ OTREZKOM PRQMOJ.

86

eSLI O FUNKCII GOWORQT, ^TO ONA WYPUKLAQ (ILI STROGO WYPUKLAQ) I NE UKAZY- WA@T NAPRAWLENIE WYPUKLOSTI, OBY^NO IME@T W WIDU WYPUKLOSTX (SOOTWETSTWENNO STROGU@ WYPUKLOSTX) WNIZ. fUNKCI@ STROGO (ILI NESTROGO) WYPUKLU@ WWERH NA- ZYWA@T TAKVE STROGO (NESTROGO) WOGNUTOJ WNIZ, A FUNKCI@ WYPUKLU@ WNIZ

WOGNUTOJ WWERH.

dLQ TOGO, ^TOBY PRIMENITX METODY DIFFERENCIALXNOGO IS^ISLENIQ K ISSLE - DOWANI@ WYPUKLYH FUNKCIJ, WYWEDEM ANALITI^ESKOE USLOWIE, \KWIWALENTNOE PRI- WEDENNOMU GEOMETRI^ESKOMU OPREDELENI@. rASSMOTRIM WYPUKLU@ WNIZ FUNKCI@ f(x) NA INTERWALE (a, b), L@BYE DWE TO^KI x1 < x2 IZ (a, b) I SOOTWETSTWU@]IE

^TO ORDINATA PROIZWOLXNOJ TO^KI M NA DUGE AB NE BOLX[E ORDINATY SOOTWETSTWU@]EJ TO^KI NA OTREZKE AB. iZ ANALITI^ESKOJ GEOMETRII IZWESTNO, ^TO TO^KA OTREZKA AB IMEET KOORDINATY

DLQ NEKOTOROGO

x3 = qx1 + (1 − q)x2; qf(x1) + (1 − q)f(x2) q (0, 1).

tO^KA M IMEET KOORDINATY x3; f(x3) . pO\TOMU OPREDELENIE WYPUKLOJ WNIZ FUNKCII \KWIWALENTNO USLOWI@:

x1, x2 (a, b) (x1 6= x2) q (0, 1) f qx1 +(1−q)x2 6 qf(x1)+(1−q)f(x2). (1)

~TOBY POLU^ITX USLOWIE DLQ WYPUKLYH WWERH , STROGO WYPUKLYH WNIZ I STROGO WYPUKLYH WWERH FUNKCIJ DOSTATO^NO W (1) NERAWENSTWO 6 ZAMENITX SOOTWETSTWENNO NA >, < I >.

oTMETIM, ^TO ESLI FUNKCIQ f(x) (STROGO) WYPUKLA WWERH, TO FUNKCIQ −f(x) (STROGO) WYPUKLA WNIZ. oGRANI^IMSQ DALEE RASSMOTRENIEM FUNKCIJ, WYPUKLYH WNIZ I STROGO WYPUKLYH WNIZ (POLU^ENNYE REZULXTATY LEGKO PERENESTI NA FUNKCII, WYPUKLYE WWERH I STROGO WYPUKLYE WWERH , ZAMENIW f NA −f). sFORMULIRUEM NESKOLXKO NEOBHODIMYH I DOSTATO^NYH USLOWIJ WYPUKLOSTI .

w SLU^AE STROGOJ WYPUKLOSTI NERAWENSTWO STROGOE .

dOK–WO. oBOZNA^IM

zAMENQQ W POSLEDNEM NERAWENSTWE (x2 − x1) NA (x2 − x3) + (x3 − x1), I PERENESQ

SLAGAEMYE S (x2 − x3) W LEWU@ ^ASTX, A SLAGAEMYE S (x3 − x1) — W PRAWU@ ^ASTX, POLU^AEM

(x2 − x3)(f(x3) − f(x1)) 6 (x3 − x1)(f(x2) − f(x3)),

87

^TO \KWIWALENTNO NERAWENSTWU IZ (2).

w SLU^AE STROGOJ WYPUKLOSTI WEZDE W RASSUVDENIQH NERAWENSTWA STROGIE . .

gEOMETRI^ESKAQ INTERPRETACIQ USLOWIQ (2): UGLOWOJ KO\FFICIENT HORDY AM NA RIS. 43 NE BOLX[E UGLOWOGO KO\FFICIENTA HORDY BM.

tEOREMA 2. pUSTX f(x) — DIFFERENCIRUEMAQ NA INTERWALE (a, b) FUNKCIQ. 1) fUNKCIQ f(x) WYPUKLA WNIZ NA (a, b) TOGDA I TOLXKO TOGDA, KOGDA EE PROIZWODNAQ

NE UBYWAET NA (a, b).

2) sTROGOJ WYPUKLOSTI f SOOTWETSTWUET STROGOE WOZRASTANIE f0.

dOK–WO 1) : PEREHODQ W (2) K PREDELU SPERWA PRI x3 → x1, A ZATEM PRI x3 → x2 I U^ITYWAQ PRAWILO PREDELXNOGO PEREHODA W NERAWENSTWE I OPREDELENIE PROIZWODNOJ, POLU^AEM

T.E. DLQ WYPUKLOJ WNIZ I DIFFERENCIRUEMOJ W INTERWALE (a, b) FUNKCII NEOBHODI- MO, ^TOBY EE PROIZWODNAQ NE UBYWALA W (a, b).

2) : DLQ STROGO WYPUKLOJ WNIZ FUNKCII f(x) WMESTO (2) SPRAWEDLIWO

pRIMENQQ K RAZNOSTQM f(x3) −f(x1) I f(x2) −f(x3) FORMULU lAGRANVA, PRIHODIM K WYWODU, ^TO SU]ESTWU@T TAKIE TO^KI c1 I c2 (x1 < c1 < x < c2 < x2), DLQ KOTORYH

tAK KAK PROIZWODNAQ f0(x) NE UBYWAET W INTERWALE (a, b), TO f0(x1) 6 f0(c1) I f0(c2) 6 f0(x2), f0(x1) < f0(x2), T.E. DLQ STROGO WYPUKLOJ WNIZ FUNKCII PROIZWODNAQ f0(x) WOZRASTAET W (a, b).

1) I 2) : PUSTX PROIZWODNAQ f0(x) NE UBYWAET (WOZRASTAET) NA INTER- WALE (a, b). dOKAVEM, ^TO FUNKCIQ f(x) WYPUKLA (STROGO WYPUKLA) WNIZ. tAK KAK FUNKCIQ f(x) DIFFERENCIRUEMA W INTERWALE (a, b), TO ONA NEPRERYWNA NA L@BOM OTREZKE [x1, x2] (a, b) I, SOGLASNO TEOREME lAGRANVA SU]ESTWU@T c1 I c2 TAKIE,

^TO a < x1 < c1 < x3 < c2 < x2 < b I

oTS@DA PRI f0(c1) 6 f0(c2) (PROIZWODNAQ NE UBYWAET) SLEDUET (2), T.E. PO TEOREME 1 WYPUKLOSTX WNIZ FUNKCII f(x), A PRI f0(c1) < f0(c2) (PROIZWODNAQ WOZRASTAET) W

(2) POLU^IM STROGOE NERAWENSTWO, SOOTWETSTWU@]EE STROGOJ WYPUKLOSTI WNIZ \TOJ FUNKCII PO TOJ VE TEOREME 1. .

gEOMETRI^ESKAQ INTERPRETACIQ USLOWIQ (3): NAKLON SEKU]EJ RASPOLOVEN MEVDU NAKLONAMI KASATELXNYH NA KONCAH OTREZKA .

tEOREMA 3. pUSTX FUNKCIQ f(x) IMEET NA INTERWALE (a, b) WTORU@ PROIZWOD- NU@.

88

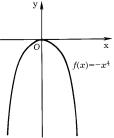
tO, ^TO TEOREMA 3 USTANAWLIWAET LI[X DOSTATO^NOE USLOWIE STROGOJ WYPUKL - OSTI WWERH (WNIZ), WIDNO IZ PROSTOGO PRIMERA DLQ FUNKCII f(x) = −x4, KOTORAQ STROGO WYPUKLA WWERH x R, HOTQ f00(x)|x=0 = −12x2|x=0 = 0 (RIS. 45).

rIS. 45

tEOREMA 4. dIFFERENCIRUEMAQ NA INTERWALE (a, b) FUNKCIQ f(x) WYPUKLA WNIZ NA NEM TOGDA I TOLXKO TOGDA, KOGDA WSE TO^KI GRAFIKA FUNKCII LEVAT NE NIVE L@BOJ KASATELXNOJ K NEMU NA \TOM INTERWALE (W SLU^AE STROGOJ WYPUKLOSTI WNIZ WSE TO^KI GRAFIKA FUNKCII, KROME TO^KI KASANIQ, LEVAT WY[E L@BOJ KASATELXNOJ K NEMU NA \TOM INTERWALE).

dOK–WO. nEOBHODIMOSTX. zAPI[EM URAWNENIE KASATELXNOJ K GRAFIKU FUNKCII

f(x) W TO^KE x0; f(x0) , GDE x0 (a, b):

y = f(x0) + f0(x0)(x − x0).

COGLASNO FORMULE lAGRANVA,

f(x) = f(x0) + f0(c)(x − x0),

GDE TO^KA c LEVIT MEVDU x I x0. pOSLE WY^ITANIQ POSLEDNEGO RAWENSTWA IZ PRE -

DYDU]EGO POLU^IM

y − f(x) = f0(x0) − f0(c) (x − x0).

dLQ STROGO WYPUKLOJ WNIZ FUNKCII, SOGLASNO ^ASTI 3 TEOREMY 2, PROIZWODNAQ WOZRASTAET. pO\TOMU ZNAK RAZNOSTI f0(x0) − f0(c) PROTIWOPOLOVEN ZNAKU RAZNOSTI x−x0 I, SLEDOWATELXNO, y−f(x) < 0 x (a, b)\{x0}. dLQ WYPUKLOJ WNIZ FUNKCII, SOGLASNO ^ASTI 1 TEOREMY 2, PROIZWODNAQ NE UBYWAET W (a, b) I PO\TOMU y −f(x) 6 0x (a, b) \ {x0}. tAK KAK y I f(x) — ORDINATY TO^EK NA KASATELXNOJ I GRAFIKE FUNKCIJ SOOTWETSTWENNO, TO TO^KI GRAFIKA FUNKCII LEVAT NE NIVE KASATELXNOJ .

dOSTATO^NOSTX. tAK KAK TO^KI GRAFIKA FUNKCII f(x) LEVAT NE NIVE L@BOJ KASATELXNOJ K NEMU W INTERWALE (a, b), TO

89

pODSTAWLQQ W (4) WMESTO x TO^KU x1 (a, x0), A ZATEM TO^KU x2 (x0, b), POLU^AEM

^TO SOOTWETSTWUET USLOWI@ (2) WYPUKLOSTI WNIZ FUNKCII f(x) W INTERWALE (a, b). sTROGOE NERAWENSTWO W (4) PRIWODIT K STROGOMU NERAWENSTWU I W (5), A \TO SOOT- WETSTWUET USLOWI@ STROGOJ WYPUKLOSTI WNIZ FUNKCII f(x) W INTERWALE (a, b). .

gEOMETRI^ESKAQ INTERPRETACIQ TEOREMY 4: DUGA GRAFIKA WYPUKLOJ WNIZ I DIFFERENCIRUEMOJ W INTERWALE FUNKCII LEVIT NE NIVE STQGIWA@]EJ \TU DUGU HORDY I NE NIVE KASATELXNOJ, PROWEDENNOJ W L@BOJ TO^KE DANNOJ DUGI (SM. RIS. 43).

27 tO^KI PEREGIBA I POSTROENIE GRAFIKOW FUNK- CIJ

sM. [iW: §8.5–8.6, 8.8 STR. 213–221, 226–241] ILI [z: STR. 242, 246–255].

27.1tO^KI PEREGIBA

pUSTX FUNKCIQ f(x) OPREDELENA I NEPRERYWNA W NEKOTOROJ OKRESTNOSTI TO^KI x0,

FUNKCII g(x) = x1/3. tO^KA x0 = 0 DLQ \TIH FUNKCIJ QWLQETSQ TO^KOJ PEREGI- BA. dEJSTWITELXNO, f0(0) = 0 I g0(0) = +∞. pO\TOMU GRAFIK FUNKCII f IMEET

GORIZONTALXNU@ KASATELXNU@ W \TOJ TO^KE , A GRAFIK FUNKCII g — WERTIKALXNU@ KASATELXNU@. kROME TOGO, f00(x) = 6x < 0 PRI x < 0 I f00(x) > 0 PRI x > 0, g00(x) =

= −2x−5/3/9 > 0 PRI x < 0 I g00(x) < 0 PRI x > 0, ^TO, ESLI U^ESTX TEOREMU 3, OZNA^AET SMENU NAPRAWLENIQ STROGOJ WYPUKLOSTI OBEIMI FUNKCIQMI PRI PEREHODE ARGUMENTA x ^EREZ TO^KU x0 = 0, T.E. TO^KA x0 = 0 UDOWLETWORQET OPREDELENI@

TO^KI PEREGIBA.

tEOREMA 5. w TO^KE PEREGIBA GRAFIK FUNKCII PEREHODIT S ODNOJ STORONY KASATELXNOJ NA DRUGU@.

dOK–WO. pUSTX x0 — TO^KA PEREGIBA FUNKCII f(x). eSLI KASATELXNAQ WERTI- KALXNA, TO GRAFIK FUNKCII NAHODITSQ PO RAZNYE STORONY OT NEE PO OPREDELENI@ . rASSMOTRIM SLU^AJ NAKLONNOJ ILI GORIZONTALXNOJ KASATELXNOJ . tOGDA PROIZWOD- NAQ f0(x0) SU]ESTWUET I KONE^NA. pUSTX SLEWA OT x0 (W INTERWALE (a; x0)) FUNKCIQ f(x) STROGO WYPUKLA WNIZ, A SPRAWA — WWERH. pO TEOREME 1 WYPOLNQETSQ USLO- WIE (2), GDE b = x0. pEREHODQ W \TOM NERAWENSTWE K PREDELU PRI x2 → x0 I ISPOLXZUQ NEPRERYWNOSTX FUNKCII W TO^KE x0, POLU^AEM

90