MAiu9

14sRAWNENIE FUNKCIJ PRI ODINAKOWOM STREMLE- NII ARGUMENTA

14.1oSNOWNYE PONQTIQ

sM. [as~, STR. 72].

pUSTX B — BAZA, α(x), β(x) — FUNKCII, OPREDELENNYE NA MNOVESTWE b B, I

zADA^A 1. wYWESTI \TI \KWIWALENTNOSTI (SM. [z, S. 140]).

14.2wY^ISLENIQ PREDELOW METODOM \KWIWALENTNYH B .M. I B.B.

tEOREMA 1 (cWOJSTWA o I O).

1) o(α) ± o(α) = o(α);

2) β = o(α), γ = o(β) = γ ESTX o(α);

3)o(α) ESTX O(α);

4)O(α) ± O(α) = O(α).

dOK–WO SLEDUET IZ OPREDELENIJ.

zADA^A 2. dOKAVITE \TU TEOREMU.

41

tEOREMA 2 (cWOJSTWA ).

(1) α(x) β(x) PO BAZE B, α(x) 6= 0 NA NEKOTOROM b B = β(x) α(x)

PO BAZE B (SWOJSTWO SIMMETRI^NOSTI );

(2) α(x) β(x) PO BAZE B α(x) = β(x) + o(β(x)) PO BAZE B (KRITERIJ

\KWIWALENTNOSTI FUNKCIJ).

dOK–WO SLEDUET IZ OPREDELENIJ.

tEOREMA 3 (O ZAMENE \KWIWALENTNYH PRI WY^ISLENII PREDELOW).

(1)lim [f(x)α(x)] = lim [f(x)β(x)];

dOK–WO SLEDUET IZ OPREDELENIJ.

oTMETIM, ^TO ISPOLXZOWATX OPREDELENIE PREDELA DLQ WY^ISLENIQ MOVNO TOLX - KO DLQ O^ENX PROSTYH PREDELOW. nAIBOLEE UNIWERSALXNYM METODOM WY^ISLENIQ PREDELOW QWLQETSQ METOD \KWIWALENTNYH B .M. I B.B., KOTORYJ ZAKL@^AETSQ W SWE- DENII SLOVNYH PREDELOW K PROSTYM, UVE IZWESTNYM. pRI \TOM ISPOLXZU@TSQ ARIFMETI^ESKIE SWOJSTWA PREDELOW, ZAMENA PEREMENNYH, KRITERIJ \KWIWALENTNO- STI FUNKCIJ I TEOREMA 3. pRI PODSTANOWKE \KWIWALENTNOSTEJ GLAWNAQ STEPENX DOLVNA SOHRANQTXSQ ILI PRI α(x) β(x) SLEDUET α(x) ZAMENQTX NA β(x) + o(β(x)) I ISPOLXZOWATX SWOJSTWA o–MALYH.

WTOROJ SPOSOB DAET NEPRAWILXNYJ OTWET.

14.3rASKRYTIE NEOPREDELENNOSTEJ

sM. [iW: §6.4, STR. 146–152].

oPREDELENIE NEOPREDELENNOSTEJ: PREDELY WIDA

hi

42

pOKAVEM, ^TO NEOPREDELENNOSTI WSEH UKAZANNYH WIDOW MOVNO SWESTI K NEOPRE - DELENNOSTI [0/0] ALGEBRAI^ESKIMI PREOBRAZOWANIQMI. w SLU^AE NEOPREDELENNOSTI [∞/∞] PREOBRAZOWANIE ESTX

f(x) = 1/g(x) . g(x) 1/f(x)

iZ NEOPREDELENNOSTI WIDA [0 · ∞] PREOBRAZOWANIEM

f(x) · g(x) = f(x) = g(x) 1/g(x) 1/f(x)

POLU^IM NEOPREDELENNOSTX WIDA [0/0] ILI [∞/∞] (WYBOR MEVDU NIMI ZAWISIT OT

SWODITSQ K NEOPREDELENNOSTI [0/0].

nEOPREDELENNYE WYRAVENIQ WIDA [1∞], [00] I [∞0] POLEZNO PREDWARITELXNO PRO-

LOGARIFMIROWATX:

ln f(x)g(x) = g(x) ln f(x).

tEPERX \TO WYRAVENIE WO WSEH TREH SLU^AQH SOOTWETSTWUET NEOPREDELENNOSTI WIDA [0 · ∞] (PROWERXTE \TO). eSLI SU]ESTWUET lim ln f(x)g(x) I ON RAWEN d R, +∞

B

lim f(x)g(x) I ON RAWEN ed, +∞

B

sLU^AI ±∞ \TOGO UTWERVDENIQ DOKAZANY W §12 (PRIMER 4 I ZADA^A 2). sLU^AJ KONE^NOGO d SLEDUET IZ NEPRERYWNOSTI \KSPONENTY I BUDET DOKAZAN POZVE .

15 nEPRERYWNOSTX FUNKCII W TO^KE

15.1oPREDELENIE I PRIMERY

sM. [z: STR. 148–151].

nAIWNOE PONIMANIE NEPRERYWNOJ LINII: LINIQ, KOTORU@ MOVNO NARISOWATX NA DOSKE, NA BUMAGE I T.P. NE OTRYWAQ MEL, KARANDA[ I T.P. OT DOSKI, BUMAGI I T.P. sTROGOE OPREDELENIE OSNOWANO NA PONQTIQH PREDELA I PRIRA]ENIQ FUNKCII .

pUSTX a E R, f : E → R, a + x E. tOGDA ^ISLO y = f(a + x) − f(a) NAZYWA@T PRIRA]ENIEM FUNKCII f W TO^KE a, SOOTWETSTWU@]EE PRIRA]ENI@ ARGUMENTA x. dRUGIE OBOZNA^ENIQ: f(a), y(a, x) I T.D.

43

rASSMOTRIM SNA^ALA WOZMOVNYE FORMULIROWKI NEPRERYWNOSTI FUNKCII f : E → R W TO^KE a E:

U(a) (OKREST. T. a) U(a) ∩ E = {a}.

tO^KI ^ISLOWOGO MNOVESTWA DELQTSQ NA DWA TIPA : IZOLIROWANNYE I PREDELXNYE.

tEOREMA 1 (OB \KWIWALENTNOSTI OPREDELENIJ NEPRERYWNOSTI FUNKCII

WTO^KE).

1.eSLI a — PREDELXNAQ TO^KA E, TO USLOWIQ S (1) PO (4) \KWIWALENTNY.

2.eSLI a — IZOLIROWANNAQ TO^KA E, TO DLQ L@BOJ FUNKCII f USLOWIQ (3) I

(4) WYPOLNQ@TSQ, A USLOWIQ (1) I (2) NE WYPOLNQ@TSQ.

dOK–WO SLEDUET IZ OPREDELENIJ.

fUNKCIQ f : E → R NEPRERYWNA W TO^KE a E (4).

sLEDSTWIE IZ TEOREMY 1: W L@BOJ IZOLIROWANNOJ TO^KE SWOEJ OBLASTI OPREDE - LENIQ FUNKCIQ NEPRERYWNA, W L@BOJ PREDELXNOJ TO^KE USLOWIQ S (1) PO (4) \KWIWALENTNY.

pRIMERY NEPRERYWNYH FUNKCIJ.

EM USLOWIE (3). pRI PROIZWOLXNOM x IZ ARIFMETI^ESKIH SWOJSTW PREDELOW IMEEM ex+Δx = exe x → ex, A ZNA^IT, WYPOLNQETSQ USLOWIE (2).

15.2sWOJSTWA FUNKCIJ, NEPRERYWNYH W TO^KE

sM. [z: STR. 156–157].

tEOREMA 2 (O NEPRERYWNOSTI ARIFMETI^ESKIH OPERACIJ). eSLI FUNKCII f I g NEPRERYWNY W TO^KE a, TO NEPRERYWNY W \TOJ TO^KE IH SUMMA, RAZNOSTX, PROIZWEDENIE, A PRI g(a) 6= 0 I ^ASTNOE f/g.

dOK–WO SLEDUET IZ SOOTWETSTWU@]EJ TEOREMY O PREDELAH , ESLI a — PREDELXNAQ TO^KA E, I IZ OPREDELENIQ, ESLI a — IZOLIROWANNAQ TO^KA E.

pRIMER 5. iZ TEOREMY 2 SLEDUET NEPRERYWNOSTX L@BOGO MNOGO^LENA.

tEOREMA 3 (O NEPRERYWNOSTI SLOVNOJ FUNKCII). eSLI FUNKCIQ g : X → Z NEPRERYWNA W TO^KE a, A FUNKCIQ f : Z → Y NEPRERYWNA W TO^KE d = g(a), TO SLOVNAQ FUNKCIQ f ◦ g NEPRERYWNA W TO^KE a.

44

dOK–WO ZAKL@^AETSQ W PROWERKE USLOWIQ (4):

tEOREMA 4 (O PEREHODE K PREDELU POD ZNAKOM NEPRERYWNOJ FUNKCII).

1) a = lim g(x) R,

pRIMER 6. iZ NEPRERYWNOSTI \KSPONENTY I TEOREMY 4 SLEDUET, ^TO

|TOT FAKT OBOSNOWYWAET IZLOVENNYJ W PREDYDU]EM PARAGRAFE METOD RASKRYTIQ NEOPREDELENNOSTE [1∞], [00] I [∞0].

oSNOWNYMI \LEMENTARNYMI FUNKCIQMI NAZYWA@T

const, xa, ax, loga x, sin x, cos x, tg x, arcsin x, arccos x, arctg x.

|LEMENTARNOJ NAZYWA@T FUNKCI@, POLU^ENNU@ IZ OSNOWNYH \LEMENTARNYH PUTEM PRIMENENIQ KONE^NOGO ^ISLA ARIFMETI^ESKIH DEJSTWIJ I OPERACII KOMPOZI - CII.

tEOREMA 5. l@BAQ \LEMENTARNAQ FUNKCIQ NEPRERYWNA W OBLASTI SWOEGO OPRE - DELENIQ.

dOK–WO SLEDUET IZ TEOREM 2 I 3, A TAKVE NEPRERYWNOSTI OSNOWNYH \LEMENTAR -

NYH FUNKCIJ (SM. [m: §9.5, STR. 275–278] ILI [z: STR. 152, 165, 166]).

45

16 nEPRERYWNOSTX FUNKCIJ NA MNOVESTWAH

sM. [z: STR. 151–153].

sWOJSTWA FUNKCII, OPREDELQEMYE EE POWEDENIEM W SKOLX UGODNO MALOJ OKRESTNO - STI NEKOTOROJ TO^KI, NAZYWA@T LOKALXNYMI SWOJSTWAMI \TOJ FUNKCII (NAPRIMER, SWOJSTWA FUNKCII, IME@]EJ W \TOJ TO^KE PREDEL, ILI SWOJSTWA FUNKCII, NEPRE- RYWNOJ W DANNOJ TO^KE). lOKALXNYE SWOJSTWA HARAKTERIZU@T POWEDENIE FUNKCII W KAKOM-TO PREDELXNOM OTNO[ENII, KOGDA EE ARGUMENT STREMITSQ K ISSLEDUEMOJ TO^KE. w OTLI^IE OT LOKALXNYH GLOBALXNYMI NAZYWA@T SWOJSTWA FUNKCII , SWQ- ZANNYE LIBO SO WSEJ EE OBLASTX@ OPREDELENIQ , LIBO S NEKOTORYM PROMEVUTKOM W \TOJ OBLASTI. nEPRERYWNOSTX FUNKCII NA MNOVESTWE ESTX GLOBALXNOE SWOJSTWO FUNKCII.

16.1oB]EE OPREDELENIE

fUNKCIQ f NEPRERYWNA NA INTERWALE (a, b), ESLI ONA NEPRERYWNA W KAVDOJ TO^KE \TOGO INTERWALA.

tEOREMA 1 (O SWQZI NEPRERYWNOSTI FUNKCII W TO^KE I NA OTREZKE).

fUNKCIQ f NEPRERYWNA NA OTREZKE [a, b] OGRANI^ENIE f [a,b] NEPRERYWNO W KAVDOJ TO^KE OTREZKA.

dOK–WO. w KAVDOJ TO^KE c INTERWALA (a, b) NEPRERYWNOSTX f \KWIWALENTNA NE-

dOKAZANNAQ TEOREMA MOTIWIRUET SLEDU@]EE OPREDELENIE . fUNKCI@ f : E → R

NAZYWA@T NEPRERYWNOJ NA PODMNOVESTWE A E, ESLI EE OGRANI^ENIE f A NEPRERYWNO W KAVDOJ TO^KE A. ~EREZ C(A) OBOZNA^A@T MNOVESTWO WSEH FUNKCIJ

NEPRERYWNYH NA MNOVESTWE A R. dALEE GOWORQ O FUNKCII f, NEPRERYWNOJ NA

PODMNOVESTWE A, BUDEM ZAMENQTX f NA f A I S^ITATX, ^TO A — OBLASTX OPREDELENIQ f.

pO OPREDELENI@ MNOVESTWO B A OTKRYTO W A R, ESLI SU]ESTWUET TAKOE OTKRYTOE W R MNOVESTWO U, ^TO B = U ∩ A. iSPOLXZUQ DANNOE PONQTIE,

46

MOVNO PEREFORMULIROWATX OPREDELENIE FUNKCII NEPRERYWNOJ NA PODMNOVESTWE SLEDU@]IM OBRAZOM.

tEOREMA 2 (KRITERIJ NEPRERYWNOSTI FUNKCII NA MNOVESTWE.). fUNK-

CIQ f : E → R NEPRERYWNA NA E OTNOSITELXNO f PROOBRAZ L@BOGO OTKRYTOGO MNOVESTWA IZ R OTKRYT W E.

dOK–WO. ” ” : RASSMOTRIM PROIZWOLXNOE OTKRYTOE MNOVESTWO V I PROIZ- WOLXNU@ TO^KU x f−1(V ). iMEEM x E I f(x) V, T.E. V — OKRESTNOSTX TO^KI

KRYTO, KAK OB_EDINENIE OTKRYTYH. iSPOLXZUQ TOVDESTWO 3 NA STR. 8 I METOD DWUH WKL@^ENIJ, POLU^AEM

U ∩ E = x f−1(V )U(x) ∩ E = x f−1(V ) U(x) ∩ E = f−1(V ),

T.E. PROOBRAZ f−1(V ) OTKRYT W E.

” ” : DOKAVEM NEPRERYWNOSTX FUNKCII f W PROIZWOLXNOJ TO^KE

pUSTX V — OKRESTNOSTX TO^KI f(x). tOGDA x f−1(V ) I PO USLOWI@ f−1(V ) — OTKRYTOE MNOVESTWO W E. pO OPREDELENI@, POSLEDNEE OZNA^AET, ^TO SU]ESTWUET TAKOE OTKRYTOE W R MNOVESTWO U, ^TO f−1(V ) = U ∩ E. t.E. U TAKAQ OKRESTNOSTX TO^KI x, ^TO f(U ∩ E) V . tAK KAK V — PROIZWOLXNAQ OKRESTNOSTX TO^KI f(x), TO FUNKCIQ f NEPRERYWNA W TO^KE x E.

16.2sWOJSTWA FUNKCIJ, NEPRERYWNYH NA OTREZKE.

sM. [z: STR. 157–159].

tEOREMA 3 (bOLXCANO–kO[I).

fUNKCIQ f(x) NEPRERYWNA NA [a, b], f(a)f(b) < 0 = c (a, b) : f(c) = 0.

tEOREMA IMEET PROSTOJ GEOMETRI^ESKIJ SMYSL: ESLI NEPRERYWNAQ LINIQ GRA- FIKA FUNKCII LEVIT I NIVE, I WY[E OSI Ox, TO \TA LINIQ PERESEKAET OSX Ox

(RIS. 14).

rIS. 14

dOK–WO. rAZDELIM OTREZOK [a, b] POPOLAM TO^KOJ d = (a + b)/2. mOVET SLU- ^ITXSQ, ^TO FUNKCIQ f(x) OBRATITSQ W NULX W \TOJ TO^KE. w \TOM SLU^AE TEOREMA DOKAZANA I c = d. pUSTX f(d) 6= 0. tOGDA NA KONCAH ODNOGO IZ OTREZKOW [a, d], [d, b] FUNKCIQ PRIMET ZNA^ENIQ RAZNYH ZNAKOW (NA RIS. 14 \TO OTREZOK [a, d]). oBOZNA^IM \TOT OTREZOK [a1, b1]. tOGDA f(a1)f(b1) < 0.

47

rAZDELIM POPOLAM OTREZOK [a1, b1] I SNOWA OTBROSIM TOT SLU^AJ, KOGDA f(x) OBRA- ]AETSQ W NULX W SEREDINE (a1 + b1)/2 \TOGO OTREZKA, IBO TOGDA TEOREMA DOKAZANA. oBOZNA^IM [a2, b2] TU IZ POLOWIN OTREZKA[a1, b1], DLQ KOTOROJ f(a2)f(b2) < 0. pRO- DOLVIM \TOT PROCESS POSTROENIQ OTREZKOW. pRI \TOM LIBO POSLE KONE^NOGO ^ISLA [AGOW NATKNEMSQ NA TAKU@ TO^KU DELENIQ OTREZKOW POPOLAM , W KOTOROJ FUNKCIQ

OBRA]AETSQ W NULX, I DOKAZATELXSTWO TEOREMY BUDET ZAWER[ENO , LIBO POLU^IM BESKONE^NU@ POSLEDOWATELXNOSTX WLOVENNYH OTREZKOW

[a1, b1] [a2, b2] . . . [an, bn] . . . ,

UDOWLETWORQ@]IH USLOWI@ DLQ WSEH n N.

pO TEOREME O WLOVENNYH OTREZKOW SU]ESTWUET TO^KA c, PRINADLEVA]AQ WSEM \TIM OTREZKAM. pOKAVEM, ^TO IMENNO \TA TO^KA UDOWLETWORQET TREBOWANIQM DAN - NOJ TEOREMY I QWLQETSQ ISKOMOJ TO^KOJ c IZ (a, b). tAK KAK bn −an = (b−a)/2n → 0 PRI n → ∞, TO

0 6 an − c 6 bn − an → 0, 0 6 S − bn 6 bn − an → 0.

A ZNA^IT, an → c I bn → c PRI n → ∞. s DRUGOJ STORONY, PO USLOWI@ TEOREMY FUNKCIQ f NEPRERYWNA W TO^KE c, PO\TOMU lim f(x) = f(c). oTS@DA I IZ OPREDELE-

tAK KAK f(an)f(bn) < 0, TO PO TEOREME O PREDELXNOM PEREHODE W NERAWENSTWE POLU -

^AEM f(c)f(c) 6 0. nO f(c)2 > 0, PO\TOMU f(c) = 0. .

dOKAZATELXSTWO TEOREMY DAET METOD RE[ENIQ NELINEJNOGO URAWNENIQ f(x) = 0 NA OTREZKE [a, b] W SLU^AE, KOGDA FUNKCIQ f NEPRERYWNA NA [a, b] I f(a)f(b) < 0.

|TOT METOD NAZYWAETSQ METOD DELENIQ OTREZKA POPOLAM.

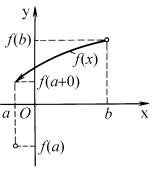
zAMETIM, ^TO TREBOWANIE NEPRERYWNOSTI FUNKCII f(x) NA OTREZKE [a, b] W USLO- WII TEOREMY 3 SU]ESTWENNO. eGO NELXZQ ZAMENITX TREBOWANIEM NEPRERYWNOSTI W INTERWALE (a, b): NA RIS. 15 DAN PRIMER GRAFIKA FUNKCII, NEPRERYWNOJ W IN- TERWALE (a, b), NO NE QWLQ@]EJSQ NEPRERYWNOJ NA OTREZKE [a, b] W SILU NARU[ENIQ NEPRERYWNOSTI SPRAWA W TO^KE a. |TA FUNKCIQ IMEET NA KONCAH OTREZKA ZNA^E- NIQ RAZNYH ZNAKOW, NO NI W ODNOJ TO^KE OTREZKA NE OBRA]AETSQ W NULX . qSNO, ^TO FUNKCIQ, IME@]AQ RAZRYW HOTQ BY W ODNOJ TO^KE INTERWALA (a, b), MOVET TAKVE PEREJTI OT OTRICATELXNOGO ZNA^ENIQ K POLOVITELXNOMU , NE OBRA]AQSX W NULX.

rIS. 15

48

sLEDU@]IJ PRIMER POKAZYWAET, ^TO W USLOWII TEOREMY NELXZQ ZAMENITX OTRE - ZOK NA DWA NEPERESEKA@]IHSQ OTREZKA.

pRIMER 1. f(x) = −1 NA [0; 1] I = 1 NA [2; 3] .

tEOREMA 4 (O PROMEVUTO^NOM ZNA^ENII). pUSTX FUNKCIQ f(x) NEPRERYWNA NA OTREZKE [a, b], A — NEKOTOROE ^ISLO, LEVA]EE MEVDU f(a) I f(b). tOGDA NAJDETSQ TAKAQ TO^KA c (a, b), ^TO f(c) = A.

dLQ DOK–WA DOSTATO^NO PRIMENITX TEOREMU 3 K FUNKCII g(x) = f(x) − A.

tAKIM OBRAZOM, NEPRERYWNAQ W PROMEVUTKE FUNKCIQ, PEREHODQ OT ODNOGO ZNA- ^ENIQ K DRUGOMU, HOTQ BY ODIN RAZ PRINIMAET KAVDOE PROMEVUTO^NOE MEVDU NIMI ZNA^ENIE. iNYMI SLOWAMI, ZNA^ENIQ, PRINIMAEMYE NEPRERYWNOJ FUNKCIEJ f(x), KOGDA x IZMENQETSQ W KAKOM-LIBO PROMEVUTKE X, SAMI TAKVE ZAPOLNQ@T SPLO[X NEKOTORYJ PROMEVUTOK Y .

tEOREMA 5 (wEJER[TRASSA OB OGRANI^ENNOSTI). nEPRERYWNAQ NA KOMPAKTE FUNKCIQ OGRANI^ENA NA NEM .

dOK–WO. pUSTX K E R, K — KOMPAKT, f : E → R — NEPRERYWNAQ NA K FUNKCIQ. pO OPREDELENI@ NEPRERYWNOJ FUNKCII NA PODMNOVESTWE OGRANI^ENIE

f K NEPRERYWNO W L@BOJ TO^KE a K. s CELX@ UPRO]ENIQ OBOZNA^ENIJ BUDEM

S^ITATX, ^TO f K = f, T.E. E = K.

eSLI a — PREDELXNAQ TO^KA K, TO lim f(x) = f(a). pO TEOREME O LOKALXNOJ

x→a

OGRANI^ENNOSTI FUNKCII, IME@]EJ PREDEL, NAJDETSQ OKRESTNOSTX U(a) TO^KI a, W KOTOROJ FUNKCIQ f OGRANI^ENA. eSLI a — IZOLIROWANNAQ TO^KA K, TO PO OPREDELE- NI@ IZOLIROWANNOJ TO^KI NAJDETSQ TAKAQ OKRESTNOSTX U(a), ^TO U(a) ∩K = {a}, A ZNA^IT, FUNKCIQ f OGRANI^ENA W U(a). sOWOKUPNOSTX TAKIH OKRESTNOSTEJ DLQ WSEH TO^EK K OBRAZUET EGO POKRYTIE. pO OPREDELENI@ KOMPAKTA MOVNO WYDELITX KO -

NE^NOE PODPOKRYTIE U(an), n = 1, N. w KAVDOJ IZ OKRESTNOSTEJ U(an) MNOVESTWO ZNA^ENIJ FUNKCII f(x) OGRANI^ENO, T.E. Cn R x U(an) |f(x)| 6 Cn. pO\TOMU

x K |f(x)| 6 C = max{C1; C2; . . . ; CN },

^TO, PO OPREDELENI@, OZNA^AET, ^TO FUNKCIQ f OGRANI^ENA NA K. .

sU]ESTWENNYM USLOWIEM W \TOJ TEOREME QWLQETSQ NEPRERYWNOSTX FUNKCII IMEN - NO NA KOMPAKTE. nEPRERYWNOSTX NA INTERWALE NE OBESPE^IWAET OGRANI^ENNOSTI FUNKCII. tAK, PRI x (0, π/2) FUNKCIQ tg x NEPRERYWNA, NO NE OGRANI^ENA. dLQ RAZRYWNOJ FUNKCII TEOREMA TAKVE NE WERNA: NAPRIMER, FUNKCIQ tg x NE OGRANI-

^ENA NA [π/4; 3π/4].

oTMETIM, ^TO OTREZOK ESTX KOMPAKT, A ZNA^IT, \TA I SLEDU@]AQ TEOREMY WERNY DLQ OTREZKA.

tEOREMA 6 (wEJER[TRASSA O DOSTIVIMOSTI NAIBOLX[EGO I NAIMENX-

[EGO ZNA^ENIJ). eSLI FUNKCIQ NEPRERYWNA NA KOMPAKTE, TO NA \TOM KOMPAKTE ESTX TO^KA, GDE FUNKCIQ PRINIMAET NAIBOLX[EE ZNA^ENIE NA \TOM KOMPAKTE , I ESTX TO^KA, GDE FUNKCIQ PRINIMAET NAIMENX[EE ZNA^ENIE.

dOK–WO. pUSTX K R — KOMPAKT, f — NEPRERYWNAQ NA K FUNKCIQ. sO- GLASNO TEOREME 5 MNOVESTWO ZNA^ENIJ FUNKCII f(x) NA K OGRANI^ENO, A SOGLAS-

NO TEOREME O TO^NOJ GRANI ONO IMEET TO^NU@ WERHN@@ GRANX M = sup f(x),

x K

49

PRI^EM M R. pREDPOLOVIM, ^TO x K f(x) < M, T.E. FUNKCIQ f(x) NE DOSTIGAET NA K SWOEJ TO^NOJ WERHNEJ GRANI. tOGDA WSPOMOGATELXNAQ FUNKCIQ

g(x) = 1/ M − f(x) , x K POLOVITELXNA WO WSEH TO^KAH K I W SILU TEOREMY O NEPRERYWNOSTI ARIFMETI^ESKIH OPERACIJ NEPRERYWNA W KAVDOJ TO^KE K. pO TEOREME 5 FUNKCIQ g(x) TAKVE OGRANI^ENA NA K, T.E. x K g(x) 6 γ, PRI^EM γ > 0. nO TOGDA f(x) 6 M − 1/γ < M, T.E. ^ISLO M − 1/γ QWLQETSQ WERHNEJ GRANX@ RASSMATRIWAEMOGO MNOVESTWA ZNA^ENIJ FUNKCII f NA K, A \TO PROTIWORE^IT OPREDELENI@ TO^NOJ WERHNEJ GRANI MNOVESTWA KAK NAIMENX[EJ IZ WERHNIH GRANEJ . iZ \TOGO PROTIWORE^IQ SLEDUET, ^TO NA K NAJDETSQ TAKAQ TO^KA x , DLQ KOTOROJ f(x ) = M, T.E. FUNKCIQ PRINIMAET W \TOJ TO^KE KONE^NOE NAIBOLX[EE ZNA^ENIE .

aNALOGI^NYM PUTEM MOVNO DOKAZATX, ^TO NA K NAJDETSQ TAKAQ TO^KA x , W KOTOROJ FUNKCIQ f(x) PRINIMAET KONE^NOE NAIMENX[EE ZNA^ENIE. .

gEOMETRI^ESKAQ INTERPRETACIQ TEOREMY 6 PRIWEDENA NA RIS. 16. nAIMENX[EE I NAIBOLX[EE ZNA^ENIQ OBOZNA^ENY SOOTWETSTWENNO m I M.

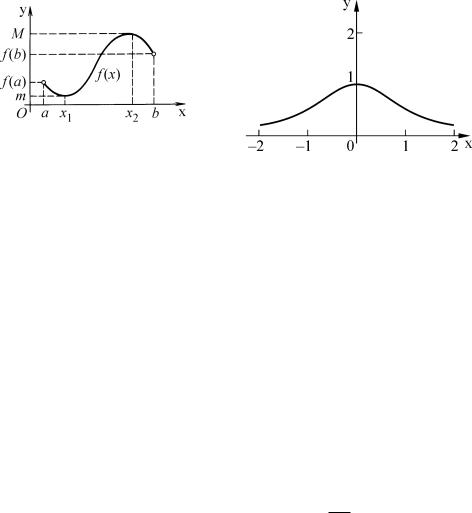
sU]ESTWENNYM USLOWIEM W \TOJ TEOREME (KAK I W PREDYDU]EJ) QWLQETSQ NEPRERYWNOSTX FUNKCII IMENNO NA KOMPAKTE (OTREZKE). dAVE SO^ETANIE NEPRERYWNOSTI I OGRANI^ENNOSTI NE GARANTIRUET DOSTIVENIQ FUNKCIEJ NAIMENX[EGO I NAIBOLX - [EGO ZNA^ENIJ: NA R FUNKCIQ 1/(1 + x2) OGRANI^ENA I NEPRERYWNA KAK \LEMENTARNAQ, NO NE DOSTIGAET NAIMENX[EGO ZNA^ENIQ (SM. RIS. 17).

iZ TEOREMY 6 I TEOREMY 4 O PROMEVUTO^NOM ZNA^ENII FUNKCII POLU^AEM

CLEDSTWIE 1. eSLI FUNKCIQ f NEPRERYWNA NA OTREZKE [a, b], TO OBRAZ OTREZKA

[a, b] PRI OTOBRAVENII f ESTX OTREZOK [m, M], GDE m = min f(x) I M = max f(x) —

x [a,b] x [a,b]

NAIMENX[EE I NAIBOLX[EE ZNA^ENIQ FUNKCII f NA OTREZKE [a, b].

|TO SLEDSTWIE ILL@STRIRUET RIS. 16: MNOVESTWO ZNA^ENIJ FUNKCII, NEPRERYWNOJ NA NEKOTOROM OTREZKE [a, b], SPLO[X ZAPOLNQET OTREZOK [m, M].

17 tO^KI RAZRYWA FUNKCIJ

pRIMERY: 1) sign x, a = 0; 2) ln x, a < 0, a = 0; 3) sinx x , a = 0.

tO^KU a R NAZYWA@T TO^KOJ RAZRYWA FUNKCII f : E → R, ESLI

1)ONA PREDELXNAQ TO^KA MNOVESTW E ∩ (−∞; a) I E ∩ (a; +∞) ,

2)FUNKCIQ f NE QWLQETSQ NEPRERYWNOJ W \TOJ TO^KE.

50