
MAiu9
.pdf
pEREHODQ K PREDELU PRI x3 → x0 W (1) I ISPOLXZUQ SU]ESTWOWANIE PROIZWODNOJ f0(x0), POLU^AEM NERAWENSTWO
f(x0) − f(x1) |
6 f0(x0). |
(2) |
x0 − x1 |
|
|
|TO NERAWENSTWO OZNA^AET, ^TO NAKLON HORDY, PROHODQ]EJ ^EREZ TO^KI A(x1; f(x1)) I B(x0; f(x0)) NE BOLX[E NAKLONA KASATELXNOJ W TO^KE B. a ZNA^IT TO^KA A LEVIT
NE NIVE KASATELXNOJ. i \TO WERNO DLQ L@BOJ TO^KI x1 (a; x0). |
|
|
|
|||||||||
rAWENSTWO W (2) OZNA^AET, ^TO TO^KA A LEVIT NA KASATELXNOJ. |
pOKAVEM, ^TO |
|||||||||||
\TO NEWOZMOVNO. rASSMOTRIM PROIZWOLXNU@ TO^KU x4 (x1, x0) I OBOZNA^IM |
||||||||||||
|
k1 = |
f(x4) − f(x1) |
, |
k2 = |
f(x0) − f(x4) |
. |
|
|
|
|||
|
|
x4 − x1 |
|
|
|
x0 − x4 |
|
|
|
|||
tOGDA IZ NERAWENSTWA (1) SLEDUET, ^TO k1 6 k2 I PO\TOMU |
|
|
|
|||||||||
f0(x0) = |
f(x0) − f(x1) |
= |
f(x0) − f(x4) + f(x4) − f(x1) |
|
= |
|||||||
|
|
|
|
|||||||||
|
x0 − x1 |
|
|
x |
|
|
||||||
|
|
x0 − 1 |
|
|||||||||
= |
k2(x0 − x4) + k1(x4 − x1) |
6 k2. |
|
(3) |
||||||||
|
|
|
|
|
|
x0 − x1 |
|
|
|
|||
tAK KAK NERAWENSTWO (2) BYLO DOKAZANO DLQ L@BOJ TO^KI x1 (a; x0), TO k2 6 oB_EDINQQ \TO NERAWENSTWO S NERAWENSTWOM (3), POLU^AEM RAWENSTWO k2 = tAKIM OBRAZOM, WSE TO^KI (x4; f(x4)), x4 (x1, x0), LEVAT NA KASATELXNOJ, T.E. GRAFIK FUNKCII f NA INTERWALE ESTX PRQMAQ, NO \TO PROTIWORE^IT
STROGOJ WYPUKLOSTI FUNKCII f NA (a; x0). pO\TOMU TO^KI GRAFIKA FUNKCII SLEWA OT x0 LEVAT STROGO NAD KASATELXNOJ.
rASSUVDAQ ANALOGI^NO, POLU^IM, ^TO TO^KI SPRAWA OT x0 LEVAT POD KASATELX- NOJ. .
pRIMER 2. fUNKCIQ
|
sh x |
PRI |
x > 0 |
f(x) = |
ln(1 − x) |
PRI |
x < 0, |
PRI PEREHODE ARGUMENTA x ^EREZ TO^KU x = 0 IZMENQET NAPRAWLENIE STROGOJ WY- PUKLOSTI (RIS. 46), POSKOLXKU PRI x < 0 f00(x) = −1/(1 −x)2 < 0 I f00(x) = sh x > 0 PRI x > 0. oDNAKO DANNAQ FUNKCIQ NE IMEET W \TOJ TO^KE PROIZWODNOJ (NI KONE^- NOJ, NI BESKONE^NOJ), A EE GRAFIK NE IMEET W SOOTWETSTWU@]EJ TO^KE KASATELXNOJ .
rIS. 46
dEJSTWITELXNO, IMEEM f−0 (0) = −1 6= f+0 (0) = 1 I PO\TOMU GRAFIK FUNKCII IMEET TOLXKO ODNOSTORONNIE KASATELXNYE W TO^KE (0; f(0) = 0), KOTORYE OBRAZU@T UGOL,
91
OTLI^NYJ OT 0 ILI π (SM. RIS. 46). nAPOMNIM, ^TO TAKU@ TO^KU NAZYWA@T UGLOWOJ TO^KOJ GRAFIKA FUNKCII. tO^KU x = 0 MY NE NAZYWAEM TO^KOJ PEREGIBA, TAK KAK NE WYPOLNQETSQ ODNO IZ USLOWIJ NA[EGO OPREDELENIQ .
wOPROS: mOVET LI TO^KA PEREGIBA BYTX TO^KOJ \KSTREMUMA ?
tEOREMA 6 (NEOBHODIMOE USLOWIE SU]ESTWOWANIQ TO^KI PEREGIBA).
eSLI FUNKCIQ f(x) DIFFERENCIRUEMA W NEKOTOROJ OKRESTNOSTI TO^KI PEREGIBA x0 I U NEE SU]ESTWUET KONE^NAQ WTORAQ PROIZWODNAQ W TO^KE x0, TO f00(x0) = 0.
dOK–WO. pO TEOREME 2 (^ASTX 2) PROIZWODNAQ f0(x) FUNKCII f(x) UBYWAET SLE-
WA OT TO^KI PEREGIBA x0 I WOZRASTAET SPRAWA ILI, NAOBOROT, WOZRASTAET SLEWA I UBYWAET SPRAWA. pO\TOMU FUNKCIQ f0(x), BUDU^I DIFFERENCIRUEMOJ, A ZNA^IT, NE-
PRERYWNOJ W TO^KE x0, IMEET W \TOJ TO^KE LOKALXNYJ \KSTREMUM. iZ NEOBHODIMOGO USLOWIQ \KSTREMUMA ZAKL@^AEM, ^TO f00(x0) = 0. .
tO^KI, W KOTORYH WTORAQ PROIZWODNAQ FUNKCII RAWNA NUL@ , BESKONE^NA ILI NE SU]ESTWUET, NAZYWA@T KRITI^ESKIMI TO^KAMI 2–GO PORQDKA FUNKCII.
tEOREMA 7 (PERWYJ DOSTATO^NYJ PRIZNAK SU]ESTWOWANIQ TO^KI PE-
REGIBA). pUSTX FUNKCIQ f(x) NEPRERYWNA W TO^KE x0, IMEET PERWU@ I WTORU@ PROIZWODNU@ W WYKOLOTOJ OKRESTNOSTI U˙ (x0) \TOJ TO^KI I SU]ESTWUET KONE^NAQ
ILI BESKONE^NAQ PROIZWODNAQ f0(x0). tOGDA
1) ESLI WTORAQ PROIZWODNAQ f00(x) MENQET ZNAK PRI PEREHODE ARGUMENTA x ^EREZ
ZNA^ENIE x0, TO x0 QWLQETSQ TO^KOJ PEREGIBA FUNKCII f(x);
2) ESLI ZNAK f00(x) NE MENQETSQ PRI PEREHODE ^EREZ x0, TO x0 NE QWLQETSQ TO^KOJ PEREGIBA FUNKCII f(x).
dOK–WO. tAK KAK SU]ESTWUET KONE^NAQ ILI BESKONE^NAQ PROIZWODNAQ f0(x0), TO
W TO^KE |
U GRAFIKA FUNKCII SU]ESTWUET KASATELXNAQ |
|
|
x0; f(x0) |
. kROME TOGO, PO |
USLOWI@ TEOREMY f00(x) |
NE MENQET ZNAK W NEKOTOROM INTERWALE SLEWA OT x0 I W |
|
NEKOTOROM INTERWALE SPRAWA OT x0.
1) eSLI ZNAKI W \TIH INTERWALAH RAZNYE, TO W SILU TEOREMY 3 NAPRAWLENIE STROGOJ WYPUKLOSTI FUNKCII f(x) W NIH RAZNOE, A ZNA^IT, x0 QWLQETSQ TO^KOJ PEREGIBA FUNKCII f(x).
2) eSLI ZNAK ODIN I TOT VE, TO NAPRAWLENIE STROGOJ WYPUKLOSTI ODINAKOWOE , I x0 NE QWLQETSQ TO^KOJ PEREGIBA. .
tEOREMA 8 (WTOROJ DOSTATO^NYJ PRIZNAK SU]ESTWOWANIQ TO^KI PERE-
GIBA). pUSTX FUNKCIQ f(x) IMEET W OKRESTNOSTI TO^KI x0 PROIZWODNYE DO PO- RQDKA n − 1 (n > 2) I PROIZWODNU@ PORQDKA n W TO^KE x0, PRI^EM f00(x0) = . . . = f(n−1)(x0) = 0, A f(n)(x0) 6= 0. tOGDA PRI NE^ETNOM n x0
FUNKCII f(x), A PRI ^ETNOM n NE QWLQETSQ.
dOK–WO. pO FORMULE tEJLORA PORQDKA n W TO^KE x0 (a, b) IMEEM
|
|
f |
(n) |
||
f(x) = f(x0) + f0(x0)(x − x0) + |
(x0) |
(x − x0)n + o (x − x0)n I PO\TOMU |
|||
|
n! |
||||
f00(x) = |
f(n)(x0) |
(x − x0)n−2 + o (x − x0)n−2 , |
|||
(n − 2)! |
|||||
92

GDE ZNAK PRAWOJ ^ASTI OPREDELQETSQ PERWYM SLAGAEMYM . eSLI n NE^ETNO, TO W
OKRESTNOSTI U(x0) WTORAQ PROIZWODNAQ f00(x) PRI PEREHODE ARGUMENTA x ^EREZ ZNA-
^ENIE x0 WMESTE S SOMNOVITELEM (x−x0)n−2 MENQET ZNAK. pO TEOREME 7 x0 — TO^KA PEREGIBA FUNKCII f(x). eSLI VE n ^ETNO, TO f00(x) W WYKOLOTOJ OKRESTNOSTI U˙ (x0)
SOHRANQET ZNAK, A ZNA^IT, TO^KA x0 NE BUDET TO^KOJ PEREGIBA.
27.2oB]AQ SHEMA POSTROENIE GRAFIKA FUNKCII
pOSTROENI@ GRAFIKA FUNKCII (TO^NEE, EGO \SKIZA) PRED[ESTWUET ISSLEDOWANIE FUNKCII, WKL@^A@]EE W SEBQ SLEDU@]IE \TAPY:
1)USTANOWLENIE OBLASTI OPREDELENIQ FUNKCII, SWOJSTW ^ETNOSTI (NE^ETNOSTI) I PERIODI^NOSTI FUNKCII;
2)POISK TO^EK RAZRYWA FUNKCII, WY^ISLENIE W NIH I W KONCEWYH TO^KAH OBLA - STI OPREDELENIQ ODNOSTORONNIH PREDELOW FUNKCII , NAHOVDENIE WERTIKALXNYH ASIM- PTOT;
3)WY^ISLENIE PROIZWODNOJ, POISK KRITI^ESKIH TO^EK 1 PORQDKA, WY^ISLENIE ZNA^ENIJ FUNKCII W KRITI^ESKIH TO^KAH;
4)WY^ISLENIE WTOROJ PROIZWODNOJ, POISK KRITI^ESKIH TO^EK 2 PORQDKA, WY^I- SLENIE ZNA^ENIJ FUNKCII W \TIH TO^KAH;
5)ISSLEDOWANIE POWEDENIQ FUNKCII PRI x → ±∞, T.E. NAHOVDENIE NAKLONNYH
ILI GORIZONTALXNYH ASIMPTOT GRAFIKA FUNKCII.
rEZULXTATY PERE^ISLENNYH \TAPOW CELESOOBRAZNO ZANOSITX W SWODNU@ TABLICU , PERWAQ KOLONKA KOTOROJ SODERVIT ZNA^ENIQ ARGUMENTA x, SOOTWETSTWU@]IE GRANI- CAM PROMEVUTKOW OBLASTI OPREDELENIQ FUNKCII , EE TO^KAM RAZRYWA, KRITI^ESKIM TO^KAM 1 I 2 PORQDKA, A TAKVE WSEM INTERWALAM OBLASTI OPREDELENIQ FUNKCII MEVDU \TIMI TO^KAMI. tO^KI, KOTORYE ZANOSQTSQ W \TU TABLICU NAZYWA@T HA-
RAKTERNYMI. w SLU^AE ^ETNOSTI ILI NE^ETNOSTI FUNKCII W TABLICU ZANOSQT TOLXKO TO^KI I INTERWALY IZ PRAWOJ POLUPLOSKOSTI I ODIN PRAWYJ INTERWAL IZ LEWOJ POLUPLOSKOSTI. w SLU^AE PERIODI^NOSTI FUNKCII W TABLICU ZANOSQT TOLXKO
TE TO^KI I INTERWALY, KOTORYE NEOBHODIMY DLQ POSTROENIQ GRAFIKA NA PERIO - DE. wTORAQ KOLONKA SODERVIT ZNA^ENIQ FUNKCII f(x) W HARAKTERNYH TO^KAH. w TRETX@ I ^ETWERTU@ KOLONKI ZANOSQT ZNA^ENIQ ILI ZNAKI f0(x) I f00(x) W WYDE- LENNYH TO^KAH I INTERWALAH. pQTAQ KOLONKA SODERVIT KRATKU@ HARAKTERISTIKU POWEDENIQ FUNKCII I OSOBENNOSTEJ EE GRAFIKA, A [ESTAQ — FRAGMENTY GRAFIKA W OKRESTNOSTI OTME^ENNYH TO^EK I W UKAZANNYH INTERWALAH .
nEPOSREDSTWENNOE POSTROENIE GRAFIKA FUNKCII NA^INAETSQ S POSTROENIQ KASA - TELXNYH W HARAKTERNYH TO^KAH W WIDE NEBOLX[IH OTREZKOW (TAM, GDE ONI SU]ESTWU- @T) I S POSTROENIQ ASIMPTOT. pOSLE ^EGO POSTROENIE GRAFIKA FUNKCII SWODITSQ K ”SGLAVIWANI@” LOMANNOJ, POLU^ENNOJ IZ OTREZKOW KASATELXNYH I ASIMPTOT .
pRIMER 3. rASSMOTRIM POSLEDOWATELXNOSTX WYPOLNENIQ UKAZANNYH \TAPOW I ZAPOLNENIQ SWODNOJ TABLICY PRI ISSLEDOWANII FUNKCII
p
f(x) = 3 x(x − 1)2.
1. fUNKCIQ OPREDELENA NA WSEJ ^ISLOWOJ OSI I NE QWLQETSQ ^ETNOJ , NE^ETNOJ ILI PERIODI^ESKOJ (\TO FUNKCIQ OB]EGO WIDA).
93

2. fUNKCIQ NE IMEET TO^EK RAZRYWA (A SLEDOWATELXNO, I WERTIKALXNYH ASIM- PTOT) I NEPRERYWNA NA WSEJ ^ISLOWOJ OSI. 3. pROIZWODNAQ FUNKCII f(x)
f0(x) = |
3x − 1 |
||
|
|
||
3p3 x2(x − 1) |
|||
|
|||
W TO^KE x0 = 1/3 RAWNA NUL@, A W TO^KAH x1 = 0 I x2 = 1 — BESKONE^NA. iSSLEDUEM POWEDENIE PROIZWODNOJ f0(x) W OKRESTNOSTI \TIH KRITI^ESKIH TO^EK FUNKCII f(x). tAK KAK
|
|
|
|
|
|
|
lim f0(x) = + |
∞ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
TO FUNKCIQ IMEET WERTIKALXNU@ KASATELXNU@ W TO^KE x1 = 0. pOSKOLXKU |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
lim |
f0(x) |
= |
|
|
lim |
|
|
|
|
3x − 1 |
|
= |
−∞ |
, |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
3 |
|
x2(x − 1) |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x→1−0 |
|
|
|
x→1−0 3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
lim |
f0(x) |
= |
|
|
lim |
|
|
p3x |
− |
1 |
|
|
= + |
∞ |
, |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
x→1+0 |
|
|
|
x→1+0 3p3 x2(x − 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
TO^KA x2 = 1 ESTX TO^KA WOZWRATA (ZAOSTRENIQ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
4. wTORAQ PROIZWODNAQ FUNKCII f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
f00(x) = − |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
3 |
|
5 |
|
|
|
|
4 |
|
|
|
|
|
|
|
x2 = 1 |
|
|
|
|
. |
|||||||||||||
NI W ODNOJ TO^KE NE OBRA]AETSQ W NULX, |
|
p |
|
|
|
|
|
|
x1 = 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
9 |
|
|
x (x − 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A W TO^KAH |
|
|
|
|
|
I |
|
|
|
|
|
|
|
NE SU]ESTWUET |
|
||||||||||||
5. tAK KAK PREDELY |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2/3 |
|
|
|
|
|
|
|
||||||||
|
|
|
f(x) |
3 |
|
x(x |
|
|
|
1)2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||
|
x→∞ |
x |
x→∞ p |
|
x− |
|
|
|
|
|
x→∞ 1 − x |
|
|
|
|
|
|
|
|
||||||||||||||||||||
I |
k = lim |
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
= 1 |
|
|
|
|
||||||||||
− |
|
x→∞ p |
− − |
|
x→∞ |
|
1 − x |
|
|
− |
|
||||||||||||||||||||||||||||
x→∞ |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2/3 |
|
|
|||
b = lim |
f(x) |
kx = lim |
3 x(x |
|
1)2 |
|
|
x |
|
= |
|
lim x |
|
|
|
|
|
|
|
|
|
|
|
|
1 = |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
x→∞ |
|
3 |
−x |
= −3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
x |
2 |
|
1 |
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
SU]ESTWU@T, GRAFIK FUNKCII f(x) IMEET DWUSTORONN@@ NAKLONNU@ ASIMPTOTU S URAWNENIEM y = x − 2/3.
s ISPOLXZOWANIEM SWODNOJ TABLICY 1 NA RIS. 47 POSTROEN GRAFIK ISSLEDUEMOJ FUNKCII, A TAKVE GRAFIKI EE PERWOJ I WTOROJ PROIZWODNYH .
94
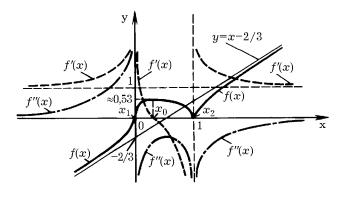
tABLICA 1
|
f (x) |
f 0(x) |
f 00(x) |
kRATKAQ |
fRAGMENT |
x |
HARAKTERISTIKA |
||||
|
|
|
|
POWEDENIQ FUNKCII |
GRAFIKA |
|
|
|
|
|
|
|
|
|
|
|
|
(−∞, 0) |
% |
+ |
+ |
wOZRASTANIE, |
|
WYPUKLOSTX |
|
||||
|
|
|
|
WNIZ |
|
|
|
|
|
|
|
x1 = 0 |
0 |
+∞ |
@ |
tO^KA PEREGIBA |
|
S WERTIKALXNOJ |
|
||||
|
|
|
|
KASATELXNOJ |
|
|
|
|
|
|
|
(0, 1/3) |
% |
+ |
− |
wOZRASTANIE, |
|
WYPUKLOSTX |
|
||||
|
|
|
|
WWERH |
|
|
|
|
|
|
|
x0 = 1/3 |
≈ 0,53 |
0 |
− |
mAKSIMUM S |
|
GORIZONTALXNOJ |
|
||||
|
|
|
|
KASATELXNOJ |
|
|
|
|
|
|
|
(1/3, 1) |
& |
− |
− |
uBYWANIE, |
|
WYPUKLOSTX |
|
||||
|
|
|
|
WWERH |
|
|
|
|
|
|
|
x2 = 1 |
0 |
∞ |
@ |
mINIMUM S |
|
WERTIKALXNOJ |
|
||||
|
|
|
|
KASATELXNOJ |
|
|
|
|
|
(TO^KA WOZWRATA) |
|
|
|
|
|
|
|
(1, +∞) |
% |
+ |
− |
wOZRASTANIE, |
|
WYPUKLOSTX |
|
||||
|
|
|
|
WWERH |
|
|
|
|
|
|
|
rIS. 47
iZLOVENNYJ METOD POSTROENIQ GRAFIKOW FUNKCIJ PO HARAKTERNYM TO^KAM MO - VET BYTX OBOB]EN NA SLU^AJ PARAMETRI^ESKI ILI NEQWNO ZADANNOJ FUNKCII . pRI \TOM W SLU^AE PARAMETRI^ESKI ZADANNOJ FUNKCII ZAPOLNQETSQ TABLICA ANALOGI^ - NAQ TABLICE 1, NO SODERVA]AQ E]E ODIN STOLBEC, STOQ]IJ SLEWA. w NEGO ZANOSQTSQ ZNA^ENIQ PARAMETRA t W HARAKTERNYH TO^KA, A TAKVE INTERWALY MEVDU NIMI. w SLU^AE NEQWNO ZADANNOJ FUNKCII POHOVU@ TABLICU ZAPOLNITX NELXZQ , TAK KAK PRO- IZWODNYE yx0 , yxx00 x, TAK I OT y. nO PLOSKOSTX xOy MOVNO RAZREZATX
95
NA OBLASTI, GDE \TI PROIZWODNYE IME@T POSTOQNNYJ ZNAK, A ZNA^IT, ISSLEDUEMAQ FUNKCIQ IMEET TOT ILI INOJ TIP MONOTONNOSTI I WYPUKLOSTI . iSPOLXZQ \TU IN- FORMACI@, HARAKTERNYE TO^KI SOEDINQ@T DUGAMI GRAFIKA NEQWNO ZADANNOJ FUNK - CII. w SOWOKUPNOSTI \TI DUGI OBRAZU@T LINI@, KOTORAQ ZADAETSQ URAWNENIEM NEQWNO ZADANNOJ FUNKCII.
27.3nAIBOLX[EE I NAIMENX[EE ZNA^ENIQ FUNKCII W PRO -
MEVUTKE
pUSTX FUNKCIQ f(x) NEPRERYWNA NA OTREZKE [a, b]. tOGDA, SOGLASNO TEOREME wEJER- [TRASSA, ONA DOSTIGAET NA \TOM OTREZKE SWOIH NAIBOLX[EGO M I NAIMENX[EGO m ZNA^ENIJ. eSLI FUNKCIQ DOSTIGAET ODNO IZ \TIH ZNA^ENIJ WNUTRI OTREZKA , TO SO- OTWETSTWU@]AQ TO^KA ESTX TO^KA LOKALXNOGO \KSTREMUMA FUNKCII f(x). pO\TOMU, DLQ NAHOVDENIQ NAIBOLX[EGO I NAIMENX[EGO ZNA^ENIJ FUNKCII f(x), NEPRERYWNOJ NA OTREZKE [a, b], NEOBHODIMO:
1)NAJTI WSE KRITI^ESKIE TO^KI FUNKCII, POPADA@]IE W INTERWAL (a, b);
2)WY^ISLITX ZNA^ENIQ FUNKCII WO WSEH UKAZANNYH KRITI^ESKIH TO^KAH ;
3)WY^ISLITX ZNA^ENIQ f(a) I f(b) FUNKCII NA KONCAH OTREZKA;
4)IZ WSEH POLU^ENNYH ZNA^ENIJ FUNKCII WYBRATX NAIBOLX[EE I NAIMENX[EE . oTMETIM, ^TO ZDESX PROWERQETSQ TOLXKO NEOBHODIMOE USLOWIE \KSTREMUMA , PROWE- RQTX DOSTATO^NOE USLOWIE NE NUVNO.
pRIMER 4. nAJDEM NAIBOLX[EE M I NAIMENX[EE m ZNA^ENIQ FUNKCII
f(x) = 2x3 − 3x2 − 36x − 8
NA OTREZKE [−3, 6]. sNA^ALA WY^ISLIM PROIZWODNU@
f0(x) = 6x2 − 6x − 36 = 6(x + 2)(x − 3).
oBE STACIONARNYE TO^KI x = −2 I x = 3 \TOJ FUNKCII PRINADLEVAT ZADANNOMU OTREZKU. zNA^ENIQ FUNKCII W STACIONARNYH TO^KAH I NA KONCAH OTREZKA :
f(−3) = 19, f(−2) = 36, f(3) = −89, f(6) = 100.
oTS@DA WIDNO, ^TO NAIBOLX[EGO ZNA^ENIQ FUNKCIQ DOSTIGAET NA ODNOM IZ KONCOW OTREZKA, T.E. M = f(6) = 100, A NAIMENX[EGO ZNA^ENIQ m = f(3) = −89 — W ODNOJ IZ STACIONARNYH TO^EK, KOTORAQ, O^EWIDNO, QWLQETSQ TO^KOJ MINIMUMA DANNOJ FUNKCII. .
27.4iSSLEDOWANIQ FUNKCIJ, ZADANNYH PARAMETRI^ESKI
pRIMER 5. pUSTX ZAWISIMOSTX y OT x ZADANA W WIDE
|
x(t) = |
|
t |
|
|
|
|
|
|
t |
R 1 . |
||
1 |
|
2 |
||||
|
|
+ t3 |
, |
|
||
y(t) = |
|
t |
|
, |
\ {− } |
|
|
|
3 |
||||
|
|
|
|
|
|
|
|
|
1 + t |
|
|
||
|
|
|
|
|
|
|
96
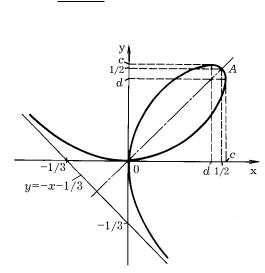
iMEEM
t→−1−0 |
( ) = +∞ |
t→−1+0 |
−∞ |
, |
t→−1−0 |
−∞ |
, |
t→−1+0 |
∞ |
lim |
x t |
, lim x(t) = |
|
lim y(t) = |
|
lim |
y(t) = + . |
kROME TOGO, PRI t0 = 0 x(t0) = y(t0) = 0 I PRI t → ∞ x(t) → 0 I y(t) → 0, T.E. KRIWAQ DWAVDY PROHODIT ^EREZ NA^ALO KOORDINAT .
nAJDEM PROIZWODNYE:
y0 |
= t |
2 − t3 |
, |
y00 |
= 2 |
(1+t3)4 |
. |
|
|
||||||
x |
|
1 − 2t3 |
|
xx |
(1 − 2t3)3 |
||
|
|
|
|
||||
rIS. 48
97
