
- •Электромагнетизм Некоторые сведения из математики
- •Лекция 1 электростатика
- •Лекция 2
- •1) Поле равномерно заряженной бесконечной плоскости.
- •2) Поле двух бесконечных параллельных плоскостей, заряженных равномерно разноимёнными зарядами с плотностями и .
- •Теорема Остроградского – Гаусса в дифференциальной форме.
- •Лекция 3 Проводники в электрическом поле
- •Электрическое поле у поверхности проводника
- •Силы, действующие на поверхность проводника
- •Свойства замкнутой проводящей оболочки
- •Общая задача электростатики. Уравнение Пуассона
- •Электроёмкость Электроёмкость уединённого проводника
- •Лекция 4 Электрическое поле в диэлектрике Электрический диполь в электрическом поле
- •Сила, действующая на диполь в электрическом поле
- •Поляризация диэлектрика
- •Вектор электрического смещения
- •Поле на границе раздела диэлектриков
- •Поле на границе проводник – диэлектрик
- •Некоторые важные следствия по теме:
- •Лекция 5 Энергия электрического поля
- •Постоянный электрический ток –
- •Уравнение непрерывности
- •Разветвлённые цепи
- •Закон Джоуля–Ленца
- •1). Однородный участок цепи
- •2). Неоднородный участок цепи
- •Лекция 6 Магнитное поле в вакууме
- •Магнитное поле равномерно движущегоя заряда
- •Закон Био – Савара
- •Основные законы магнитного поля
- •1). Магнитное поле прямого тока I:
- •2). Магнитное поле соленоида, по которому протекает ток I:
- •3). Магнитное поле тороида:
- •Лекция 7 Проводники с током в магнитном поле Закон Ампера
- •Момент сил, действующих на контур с током
- •Магнитное поле в веществе
- •Вектор вектор напряжённости магнитного поля
- •Магнитное поле на границе раздела магнетиков
- •Лекция 8
- •Движение заряженных частиц в электрическом и
- •Магнитном полях
- •Движение заряженных частиц в постоянном магнитном поле
- •Отклонение движущихся заряженных частиц электрическим и магнитным полями
- •Ускорители заряженных частиц
- •Преобразования Лоренца для электрических и магнитных полей
- •Электромагнитная индукция
- •Природа электромагнитной индукции
- •Явление самоиндукции
- •Взаимная индукция
- •Энергия магнитного поля
- •Магнитное давление
- •Лекция 10 Уравнения Максвелла для электромагнитного поля
Лекция 2
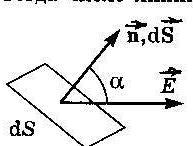 Число
линий, пронизывающих элементарную
площадкуdS
, нормаль
Число
линий, пронизывающих элементарную
площадкуdS
, нормаль
![]() которой составляет уголα
с вектором
которой составляет уголα
с вектором
![]() определяют как
определяют как![]() .
Эту величину называют потоком
.
Эту величину называют потоком![]() вектора
вектора![]() сквозь площадкуdS:
сквозь площадкуdS:
![]() .
.
Если имеется
некоторая произвольная поверхность S
, то поток вектора
![]() сквозь неё
сквозь неё
![]() .
.
Эта величина
алгебраическая. В случае замкнутых
поверхностей, положительное направление
нормали
![]() принято выбиратьнаружу
области, охватываемой этими поверхностями
(внешняя нормаль).
принято выбиратьнаружу
области, охватываемой этими поверхностями
(внешняя нормаль).
Теорема
Остроградского – Гаусса:
поток вектора напряжённости
электростатического поля в вакууме
сквозь произвольную замкнутую поверхность
равен отношению алгебраической суммы
электрических зарядов, находящихся
внутри этой поверхности, к электрической
постоянной
![]() .
.
![]() .
.
Если заряды
распределены непрерывно с объёмной
плотностью
![]() ,
зависящей от координат, то
,
зависящей от координат, то
![]() ,
,
Где интегрирование производится только по объёму, заключённому внутри замкнутой поверхности S.
Если поле создаётся
системой точечных зарядов
![]() , то
, то![]() .
Тогда
.
Тогда
![]() .
.
Само поле
![]() зависит от
конфигурации всех зарядов, а поток
зависит от
конфигурации всех зарядов, а поток
![]() сквозь
произвольную замкнутую поверхностьS
определяется только алгебраической
суммой зарядов внутри
поверхности
S.
сквозь
произвольную замкнутую поверхностьS
определяется только алгебраической
суммой зарядов внутри
поверхности
S.
Применение теоремы Остроградского – Гаусса.
1) Поле равномерно заряженной бесконечной плоскости.
Бесконечная
плоскость заряжена с постоянной
поверхностной плотностью
![]() . Линии напряжённости перпендикулярны
рассматриваемой плоскости и направлены
от неё в обе стороны.
. Линии напряжённости перпендикулярны
рассматриваемой плоскости и направлены
от неё в обе стороны.
В качестве Гауссовой поверхности примем поверхность цилиндра, образующие которого перпендикулярны заряженной плоскости и лежат по разные стороны от неё.
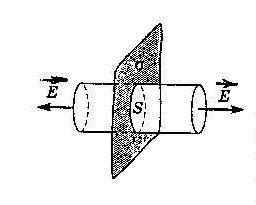
Поток через боковую
поверхность цилиндра равен нулю. Поэтому
полный поток через всю поверхность
![]() .
Внутри цилиндра заключён заряд
.
Внутри цилиндра заключён заряд![]() .
.
По теореме
Остроградского – Гаусса
![]() .
.
Полученный результат справедлив только для бесконечной плоской поверхности, однако он приближённо справедлив и для области, прилегающей к средней части конечной равномерно заряженной плоской поверхности, вдали от её краёв.
2) Поле двух бесконечных параллельных плоскостей, заряженных равномерно разноимёнными зарядами с плотностями и .
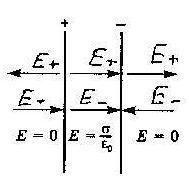 Это
поле можно легко найти как суперпозицию
полей, создаваемых каждой из плоскостей
в отдельности.
Это
поле можно легко найти как суперпозицию
полей, создаваемых каждой из плоскостей
в отдельности.
Поле сосредоточено между плоскостями и является однородным в этой области.
3)
Поле бесконечного круглого цилиндра
радиуса R
(или бесконечной нити), заряженного
равномерно по поверхности так, что на
единицу длины приходится заряд
![]() .
.
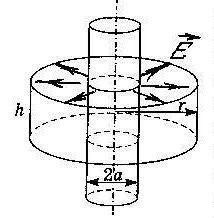
Из соображений
симметрии следует, что поле здесь имеет
радиальный характер, т.е. вектор
![]() в каждой точке перпендикулярен оси
цилиндра, а модуль вектора
в каждой точке перпендикулярен оси
цилиндра, а модуль вектора![]() зависит только от расстоянияr
до оси цилиндра.
зависит только от расстоянияr
до оси цилиндра.
Возьмём замкнутую
Гауссову поверхность в форме коаксиального
прямого цилиндра радиуса r
и высотой
h
. Тогда
![]() , а
, а![]() .
.
По теореме
Остроградского – Гаусса
![]()
для
![]() иЕ
= 0 при r
< R
т.к. внутри цилиндра зарядов нет. Внутри
равномерно заряженного по поверхности
круглого бесконечного цилиндра поля
нет.
иЕ
= 0 при r
< R
т.к. внутри цилиндра зарядов нет. Внутри
равномерно заряженного по поверхности
круглого бесконечного цилиндра поля
нет.
4) Поле сферической поверхности радиусом R, заряженной равномерно зарядом q.
Это поле центрально
симметричное. Возьмём в качестве
замкнутой Гауссовой поверхности
концентрическую сферу радиусом r
> R.
Тогда
![]() .
.
По теореме
Остроградского – Гаусса
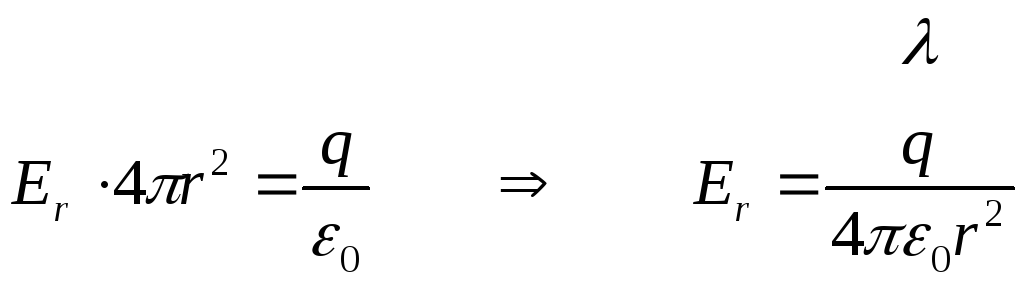 .
.
При r < R замкнутая поверхность не содержит внутри зарядов и поэтому внутри заряженной сферы Е = 0.
5)
Поле равномерно заряженного шара.
Пусть заряд q
равномерно распределён по шару радиусом
R.
Здесь
поле также центрально симметричное.
Вне шара (r
> R)
поле такое же как от заряженной сферы
или точечного заряда
![]() .
.
Внутри шара для
замкнутой поверхности в виде сферы
радиусом r
< R
имеем
![]() и
и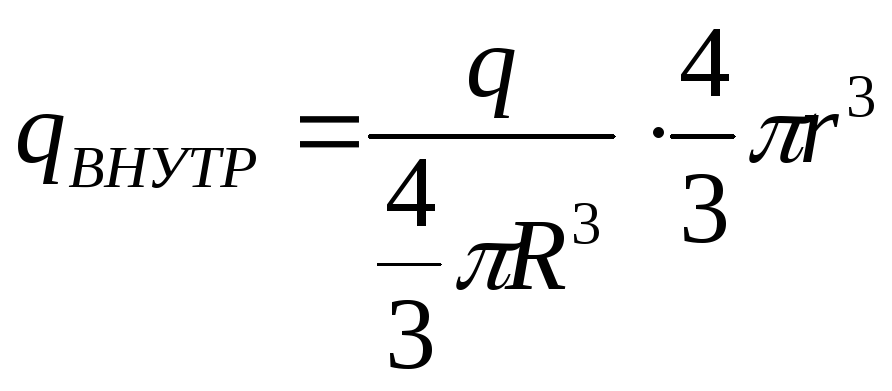 .
.
По теореме
Остроградского – Гаусса
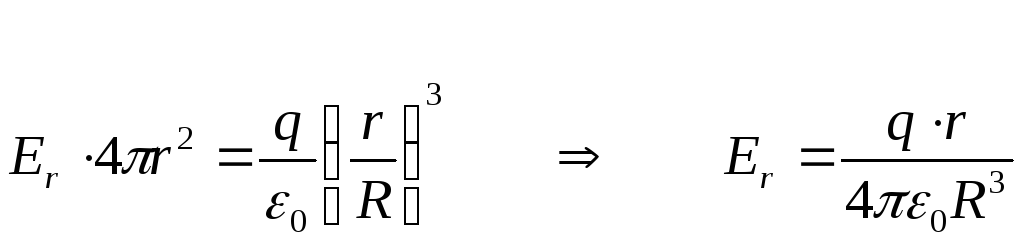
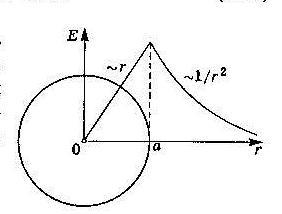
Внутри шара напряжённость растёт линейно с расстоянием r от его центра.
