Методические указания

Тогда количество информации, содержащееся в одном сообщении, будет:

m

=−n∑ p(xi )log p(xi ) [дв.ед.].

i=1

Количество информации, приходящееся на один элемент сообщения, называют удельной информативностью или энтропией:

Энтропия характеризует степень или меру неопределенности источника сообщений с заданным алфавитом. Чем больше энтропия, тем больше информации несет в себе сообщение источника, тем большая неопределенность снимается при получении сообщения.

Выражение (2.1) представляет собой классическую формулу Шеннона для определения энтропии сообщения с неравновероятным и независимым распределением символов. Эта формула получена в развитие формулы Хартли, предложенной для определения количества информации в сообщении с равновероятным и независимым распределением символов.

Приведенная формула К. Шеннона переходит в формулу Хартли при равных вероятностях символов, образующих сообщение, то есть при

Соотношение энтропии и количества информации.

Если энтропия является мерой неопределенности случайного состояния некоторой системы, то количество информации характеризует меру уменьшения или снятия неопределенности состояния этой системы. ЭнтропияH(X ), выра-

жающая среднюю неопределенность состояния системы, является априорной характеристикой и может быть вычислена до эксперимента, если известна статистика состояний. Количество же информации I(X ) определяется апостери-

орно, т.е. в результате эксперимента. Численное совпадение H(X ) и I(X )

22

возможно лишь в том случае, если эксперимент полностью снимает априорную неопределенность.

Энтропию H(X ) можно рассматривать и как некоторую простейшую число-

вую характеристику случайной величины x и ее законов распределения. Выражение (2.1) раскрывает смысл энтропии как статистического параметра случайной величины, о чем уже было сказано. Если пренебречь математическими строгостями, то выражение (2.1) может быть получено, исходя из того, что энтропия представляет собой среднее количество информации, приходящееся на один отсчет.

Как было ранее показано, в случае равновероятного и независимого распределения символов x (или уровней сигналов S ) энтропия имеет следующее выражение:

H0 (X ) =logm =−log p(S) [отсчетдв.ед. ], где S x .

При неравновероятном и независимом распределении символов, в соответствии

с определением энтропии, необходимо определить среднее значение величи-

ны−log p(S) .

Если в общем случае математическое ожидание определяется как

m'

MO = ∑ p(a j ) a j ,

j =0

то в рассматриваемом случае:

m

H(S) =− ∑ p(S j ) log p(S j ) ,

j =0

где p(S j )соответствует величине p(аj ), а −log p(S j ) — величине аj .

Выражение (2.1) может быть получено также в результате следующих упрощенных рассуждений:

m

= − ∑ p(S j ) log p(S j ),

j =1

23

m

где ∑ p(S j )=1, причем множитель −log p(S j ) внесен под знак суммы на j =1

основании того, что все p(S j ) одинаковы. Приведенное при этом выражение

совпадает с выражением (2.1), полученным в результате более строгого доказа-

тельства, вследствие чего может быть использовано для определения величины

H1(S) .

2.5. Определение количества информации в сообщении, состоящем из неравновероятных и зависимых символов. (Случай 3).

В реальных условиях символы (отсчеты), образующие сообщения, взаимосвязаны, что необходимо учесть в выражении для энтропии. Величина энтропии H2 (S) с учетом взаимосвязи между двумя символами может быть выражена

по аналогии с выражением (2.1.) и представлена в виде:

В случае учета взаимосвязи между любимы тремя символами энтропия будет иметь вид:

В общем случае, при учете взаимосвязи между r – символами, получим:

при

24

∑∑K∑ p(S j ,Sp ,K,Sl)=1.

j p l

По мере учета взаимосвязи между символами степень неопределенности уменьшается, в связи с чем имеет место соотношение:

2.6. Относительная энтропия и избыточность сообщений (сигна-

лов).

Приведенное соотношение (2.5) является следствием того, что при нарушении равновероятностного закона распределения символов, образующих сообщения, либо при учете статистической взаимосвязи между символами неопределенность сообщений (сигналов) падает, а следовательно, уменьшается и энтропия. Идеальные сообщения, имеющие максимальную энтропию, являются оптимальными в том смысле, что в них на один символ (элемент, уровень сигнала) приходится наибольшее количество информации.

В реальных сообщениях символы всегда коррелированы между собой, вследствие чего количество информации, приходящееся на один символ (энтропия), будет меньше, чем для идеальных сообщений. Соотношение реальных и оптимальных сообщений может быть выражено посредством коэффициента сжатия

(относительной энтропии) μ(S)или коэффициента избыточности

ство (2.6) показывает, какую часть энтропия реальных сообщений составляет от энтропии оптимальных сообщений, а также какую часть длина оптимальных сообщений составляет от длины реальных сообщений.

Равенство (2.6) указывает на то, что одно и то же количество информации I(S)может содержаться в сообщении, состоящем из nr символов с энтропией

Hr (S) или из n0 символов с энтропией H0 (S)т.е.

I(S) =nr Hr (S) =n0 H0 (S)

Коэффициент избыточности может быть представлен в виде:

25

Коэффициент избыточности показывает, какая часть реального сообщения, передаваемого или оптимального, могла бы не передаваться, если учесть вероятностные характеристики сообщения на приемном конце. Одновременно с этим этот коэффициент показывает, какая часть символов реального сообщения является излишней.

Из выражения (2.7) следует:

а) уменьшить избыточность можно за счет увеличения энтропии сообщений, что связано с приближением к равновероятностному закону распределения символов; б) увеличение избыточности приводит к увеличению времени передачи инфор-

мации, так как nr > n0 ;

в) наличие избыточных символов при одном и том же количестве информации, содержащемся в сообщении, повышает верность передачи сообщений.

Таким образом, основными параметрами теории информации являются: 1. Энтропия для случаев:

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

∑∑K∑ p(S j ,Sp ,K,Sl)=1.

j p l

H0(S) > H1(S) > H2 (S) >KHr (S).

26

2. Относительная энтропия и избыточность:

μ(S)= Hr (S) ; ϕ(S)=1−μ(S).

H0 (S)

3. Пропускная способность и скорость передачи информации:

2.7. Энтропия и ее основные свойства.

Энтропия — мера неопределенности случайной величины с конечным числом исходов, определяемая как среднее количество информацииI(S), приходящееся на один символ сообщения (элемент сигналаS ).

При равновероятном и независимом распределении символов (элементов сигнала) выражается как

H0 (S) = I(nS) [символдв.ед. ],

а при неравновероятном и независимом распределении символов

i=1

где m — число символов сообщения (элементов сигнала); p(Si ) — вероятность исхода величины Si .

Энтропия, как численная величина, — величина вещественная, ограниченная и неотрицательная. Для подтверждения этого воспользуемся выражением (2.1):

H(X ) =− m p(x )log p(x ),

∑ i i i=1

которое характеризует математическое ожидание частных состояний системы. а) Энтропия — величина вещественная, поскольку принимает значение, равное нулю только в случае детерминированного состояния системы.

27

Пусть вероятность одного из состояний системы p(x) =1, тогда вероятности всех других состояний p(x j ) =0.

В этом случае, согласно (2.1.):

H(X ) = p(xi )log p(xi ) − ∑ p(x j )log p(x j )

j=1 j≠i

Первое слагаемое в правой части равно нулю, так как 1 log1=0. Второе слагаемое правой части при p(x j ) →0 также обращается в нуль. Действительно

сумма всех слагаемых также равна нулю.

б) Энтропия — величина ограниченная , поскольку имеет предельное значение максимума каждое из слагаемых − p(xi )log p(xi ).

Действительно, беря производную от этого выражения и приравнивая ее к нулю, получаем:

p(xi ) e =1 и p(xi ) =1e =0,37 , вследствие чего значение p(xi ), при котором слагаемые имеют максимум, будет

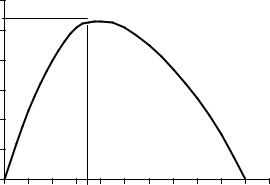
p(xi )log p−1(xi ) =1e loge =0,531.

График изменения слагаемых приведен на рис.2.1.

28

2). Величина энтропии H1(X ) = H(X )min =0, если исходы символов известны заранее, то есть, если известно, что p(x0 ) =0 и p(x1) =1, то

H1(X ) =−0log0 −1log1=0.

В этом случае неопределенность в сообщении, то есть неопределенность в выборе символов отсутствует, вследствие чего энтропия сообщения равна нулю. 3). Задавая различные значения p(x0 ) и p(x1) , можно определить характер

изменения H1(X ) , например, при p(x0 ) =0,25 и p(x1) =0,75, получим

H1(X ) =−0,25log0,25−0,75log0,75 0,8 [символдв.ед. ]. При p(x0 ) =0,01и p(x1) =0,99 найдем

H1(X ) =−0,01log0,01−0,99log0,99 0,08 [символдв.ед. ].

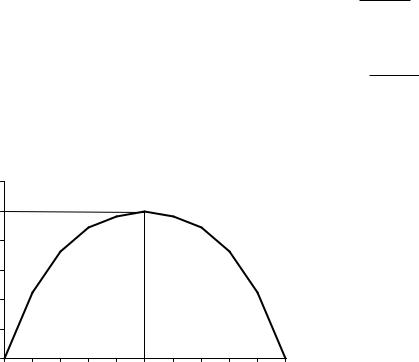
График изменения энтропии для рассмотренного случая приведен на рис.2.2.

4). В общем случае энтропия H1(X ) , как статистический параметр, характери-

зует степень неопределенности некоторой системы с m различными состояниями при максимальном значении энтропии:

Совместная энтропия статистически независимых источников.

30

Пусть имеются два статистически независимых источника X и Y, причем мно-

Откуда следует, что совместная энтропия статистически независимых источников равна сумме энтропий этих источников. Этот вывод распространяется и на большее число статистически независимых источников.

Условная энтропия статистически зависимых источников.

Для оценки количества информации, создаваемого статистически зависимыми источниками, может быть использована так называемая условная энтропия.

Пусть имеются два статистически зависимых источника сообщений X и Y, каждый из которых характеризуется условиями, изложенными выше.

Если источники X и Y коррелированы, то это означает, что между сигналами этих источников xi и y j существует взаимосвязь, при которой любому значе-

нию, например xk (рис.2.3), могут соответствовать с различной степенью веро-

ятности различные значения сигналов источника Y, т.е.

p(y1 / x1);K; p(y j / xi );K; p(ym / xn ).

31