1.Отображения. Виды отображений. Композиция отображений. Примеры.

1) f:XY – отображение с областью задания X и областью значений Y, если xX  f(x)Y.

2) Пусть f:XY – отображение, если Y=X, то f – преобразование мн-ва X. 3) –– Imf={f(x)| xX} – образ мн-ва X при действии отобр. f. 4) –– f^1(y)={xX| f(x)=y}– преобразование элемента y при отображении f. 5) Отобр. f:XY – сюрьективно (отображение на), если Imf=Y (т.е. yY  xX: f(x)=y). 6) Отобр. f:XY – инъективное, если x=x  f(x)f(x), где x,xX.

7) Отобр. f:XY – биективное, если f – сюрьективно и инъективно. 8) Пусть f:XY и g:AB – отображения; f и g одинаковые (совпадают), если: 1. X=A, Y=B и 2. f(x)=g(x) xX. Пр.: f:RR (x|x²), g:RR₊ (x|x²), H:R₊R₊ (x|x²), т.е. f,g,h – все разные.

9) e_x – единичное (тождественное) преобразования мн-ва X, если e_x:XX (x|x). 10) ] f:UV, g:VW, то fg:UW (ug(f(u)) – композиция отобр. f и g). Замеч.: f:XX, g:XX, тогда, вообще говоря, fggf. Пр.: f:a|b, b|a и g:a|a, b|a, X={a,b}, тогда fg: a|b, b| b и gf:a|a, b|a. 11) ] f:XY, g:YX, если fg=e_Y и gf=e_X, то отображение g – обратное к f и обозначается f^1. 12) 1.] X – конечное мн-во, |X| - мощность мн-ва X и равна числу элементов этого мн-ва (X=|X|); 2. мн-ва X и Y равномощны, если :XY: – биективно; 3. мн-во X – счетное, если X и N – равномощны.

2. Обратное отображение. Критерий обратимости отображения.

Утв.: Отображение f:XY – обратно  f– биективно. ◄Для док-ва потребуется Лемма. L1: Если f:XY, g:YX, т.ч. fg=e_Х, то f– инъективно, g– сурьективно ■ Покажем, что f– инъективно. Допустим, что f– не инъективно, т.е.  x,xX, т.ч. f(x)=f(x) (x=x). Тогда x=e_X(x)=g(f(x))=g(f(x))= =e_X(x)=x, т.е. получено противоречие с условием допущения (xx), т.е. f– инъективно. Покажем, что g– сурьективно. ] xX (произвольное). Заметим, что xe_X(x)=gf(x)=g(f(x))=x. Рассмотрим y=f(x)Y, тогда g(y)=g(f(x))=e_X(x)=x  по определению g– сурьективно. ■ Докажем утверждение:  т.е. из обратимости f  f– биективно. Но т.к. f– обратимо, то  g:YX: g– обратное к f, т.е. fg=e_Y и gf=e_X  по L1 g– инъективно и f– сурьективно (fg=e_Y), g– сурьективно и f– инъективно (gf=e_X)  f– биективно.  Покажем, что если f– биективно, то f– обратимо. Т.к. f– биективно, то yY xX: f(x)=y. Рассмотрим отобр. g: YX (y|x: f(x)=y). Но gf(x)=g(y)=x, т.е. gf=e_X, и fg(y)=f(x)=y, т.е. fg=e_Y. По определению g – обр. отобр. к f, т.е. f– обратно►. Св-ва: 1. f: XY – биективно  f^1– биективно. 2. f:XY, h:YZ – биективное отображение (обратимо), тогда hf– биективно (обратимо) и (hf )^1=f^-1h^1◄Доказывается с помощью полной росписи определения биективности и обратимости►. Пр.: 1) Z, Q – счетные мн-ва,  : ZN – биективно,  g: QN – биективно, но NZQ ( ) ◄►. 2) R – несчетное мн-во.

3. Бинарные отношения на мн-вах. Отношение эквивалентности. Примеры.

Def: ] X и Y –мн-ва. Всякое подмножество OXY– бинарное отношение между мн-вами X и Y. Если Y=X, то OXX – бинарное отношение на мн-ве X. Говорят, что эл-нт xX находится в отношении O с элементом yY, если (x,y)O. Иногда в качестве отношения используют обозначение напр., S т.е. элементнт x находится в отн. S с эл-том y (обозн. xSy), если (x,y)O_SXY. Пр.: 1. X=Y=R, рассмотрим отношение <. a<b, т.е. (a,b)O <, если число a меньше b; O_<={(a,b)| a,bR и a меньше b}.

– обозначение отношения на X. О_– само отношение на X (т.е. О_XX), (x,y)О_. Пр.: 2. Бинарное отношение на X, |X|=3. ]X={1,2,3}. Обозначим это отношение через :

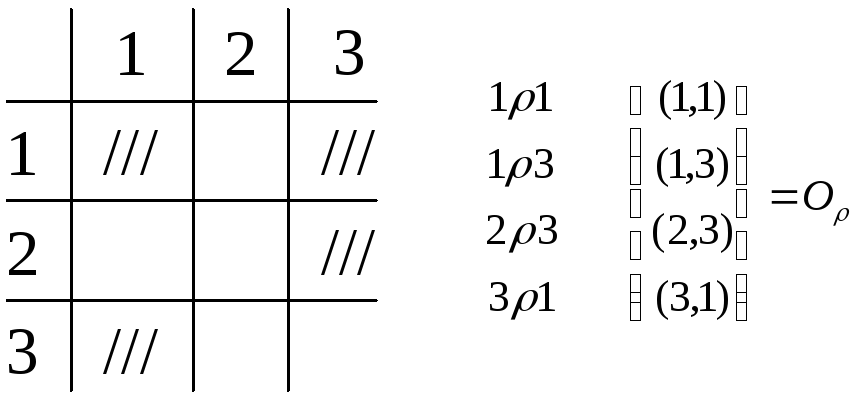
Def: Бинарное отношение  на мн-ве X называется отношением эквивалентности, если 1) xX xx (т.е. (x,x)O_)– рефлективность; 2) если xy, то yx (т.е. (x,y)O_, то (y,x)O_)– симметричность; 3) если xy, yz, то xz (т.е. если (x,y)O_ и (y,z)O_, то (x,z)O_)– транзитивность. Def: ]  отношение эквивалентности на мн-ве X. Мн-во x={yX| yx} называется классом эквивалентности, причем любой элемент из x– называется представителем класса эквивалентности. Утв.: ]  – отношение эквивалентности на X, х и хX, тогда x=x  xx◄ ] xx, пусть xx, тогда из xx  xx ^транз xx  xx  xx . Т.к. из xx  xx, то выполняя аналогичные преобразования получим xx, т.е. x=x. , т.е. xx и xx, то xx(по определению). ► Из x=x след.: axx.