Шпоры по дискре (3 семестр)
.doc|
ОГЛАВЛЕНИЕ 1. Определение поля. Обратимые элементы. Критерий поля. Примеры полей. 2. Поле частных коммутативного кольца без делителей нуля. 3. Простые поля. Классификация простых полей. 4. Расширения полей. Конечное расширение поля. 5. Степень конечного расширения поля. Теорема о башне полей (без доказательства). Примеры. 6. Простое расширение поля. Алгебраическое и трансцендентное расширения полей. 7. Классификация простых расширений полей. 8. Поле разложения многочлена. Существование и единственность поля разложения многочлена. 9. Конечные поля. Свойства конечных полей. 10. Способы вычисления обратного элемента конечного поля. 11. Существование и единственность конечного поля. 12. Х-матрицы над полем. Элементарные преобразования. Канонический вид Х-матрицы. 13. Существование канонического вида Х-матрицы. 14. Инвариантные делители Х-матрицы. Свойства инвариантных делителей. 15. Единственность канонического вида Х-матрицы. 16. Подобие матриц над полем. Критерий подобия матриц над полем. 17. Сопровождающая матрица многочлена над полем и ее свойства. 18. Существование и единственность представления матрицы над полем в 1~ нормальной форме. 19. Существование и единственность представления матрицы над полем во 2- Й нормальной форме. 20. Минимальный многочлен линейного преобразования и способы его вычисления. 21. Граф линейного преобразования линейного пространства над конечным полем. Циклы и деревья. 22. Свойства графа линейного преобразования, заданного с помощью нильпотентной матрицы. 23. Построение графа линейного преобразования, заданного с помощью нильпотентной матрицы. 24. Свойства графа линейного преобразования, заданного с помощью обратимой матрицы. 25. Цикловые термы. Сведение задачи построения графа линейного преобразования, заданного с помощью обратимой матрицы, к задаче построения графа линейного преобразования, заданного с помощью сопровождающей матрицы степени неприводимого многочлена. |
26. Построения графа линейного преобразования, заданного с помощью сопровождающей матрицы степени неприводимого многочлена (без доказательства). 27. Линейные рекуррентные последовательности (ЛРП) над конечным полем. Характеристический многочлен ОБОЗНАЧЕНИЯ .АВ – А подмножество В А<В – А подполе В a|b – a делит b degA – степень А - отношение эквивалентности АВ – А подобно В – изоморфизм
charP – характеристика поля Р [P’:P] – степень расширения P’ поля P
Re – реальная часть комплексного числа Im – мнимая часть комплексного числа НОК – наименьшее общее кратное НОД – наибольший общий делитель |P| - число элементов в Р Р\{0} – Р=<M> - Р порождено М А~В – А эквивалентна В А* - обратимая к А
Р[x] – множество многочленов над полем P S(f()) – сопровождающая матрица многочлена f() (V,E) – граф, V – множество вершин, E – множество ребер |
|
1. (1 из 1) Определение поля. Обратимые элементы. Критерий поля. Примеры полей. |
2. (1 из 3) Поле частных коммутативного кольца без делителей нуля. |
|
Определение:
1)
2)
Пример поля:
1.
2.
3. Единица относительно
4.
Определение:
!!операции определены те же, что и над полем!!
Утверждение (Критерий):
Пусть
1.
2.
◄Надо доказать►
|
Определение:
Пусть
1.
2.
Изоморфное вложения
Теорема:
◄1. Рассмотрим множество
На множестве
|
|
2. (2 из 3) Поле частных коммутативного кольца без делителей нуля. |
2. (3 из 3) Поле частных коммутативного кольца без делителей нуля. |
|
а)
б)
Проверим корректность
задания этих операций:
Непосредственной проверкой
покажем, что
— коммутативное кольцо; —
—
[…] – означает, что в качестве элемента выступает класс Покажем,
что
Рассмотрим
- изоморфизм
-сюрьективность:
-гомоморфизм:
|
Далее
заметим, что
Таким
образом
2. Докажем единственность: Пусть
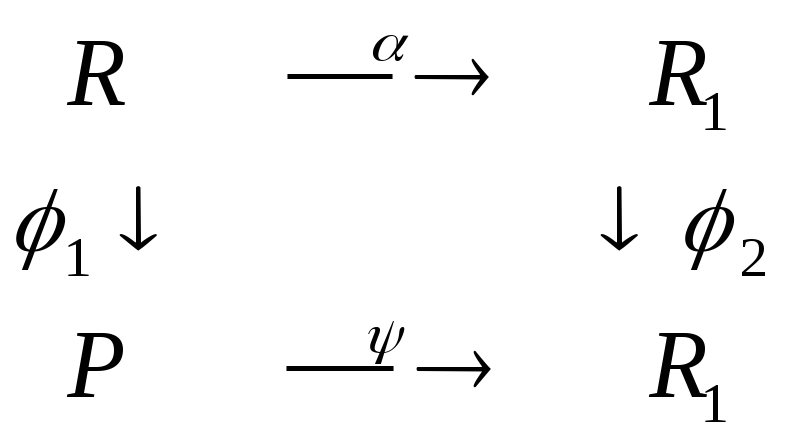
Другими словами имеет место диаграмма:
Рассмотрим
отображение
Непосредственной
проверкой покажем, что
|
|
3. (1 из 1) Простые поля. Классификация простых полей. |
3. (2 из 3) Простые поля. Классификация простых полей. |
|
Определение:
Поле
Зам Минимальное число элементов в поле – два (ноль и единица)
Определение:
Обозначения:
Пример:
1)
Таким образом
2)
Свойства характеристики поля:
1° Если
◄
2° Если ◄Доказательство следует из того,что единичные элементы поля и подполя совпадают► Пример:
1)
|
Лагранжа
2)
Утв. 1:
◄Пусть
Докажем, что
Утв. 2: (какие простые поля сущ-ют)
Пусть
1)
2)
◄Рассмотрим
Пример:
|
|
3. (3 из 3) Простые поля. Классификация простых полей. |
4. (1 из 1) Расширения полей. Конечное расширение поля. |
|
Проверить, что
Найдем
Возможны два случая:
1)
Но
Но поле частных
2)
Рассмотрим
Т
Но
|
Определение:
Пусть
Определение:
Пусть
Обозначение:
Утверждение:
◄1)
2)
Но
Определение:
Расширение
Замечание:
|


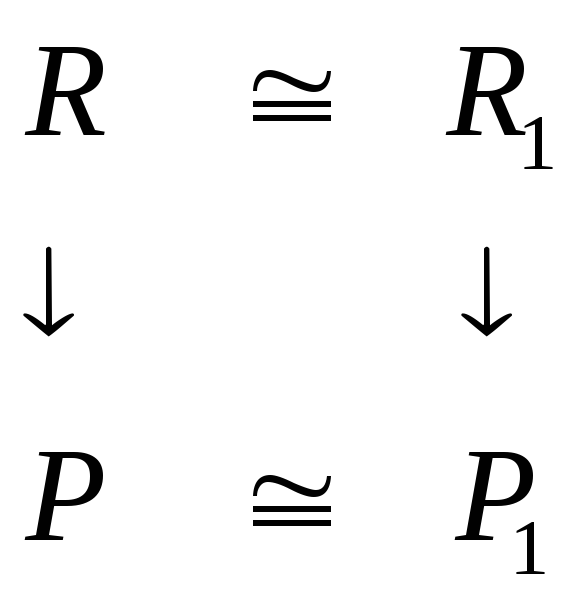 (поле частных единственно с точностью
до изоморфизма.)
(поле частных единственно с точностью
до изоморфизма.)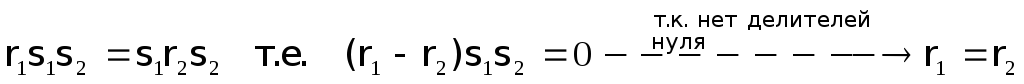 Мы получили противоречие.
Мы получили противоречие.
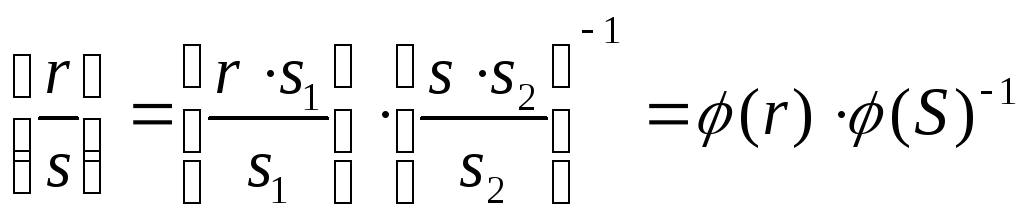
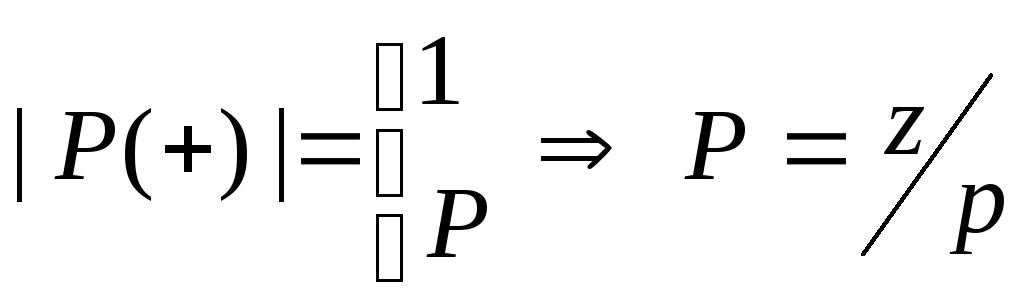
 огда
огда