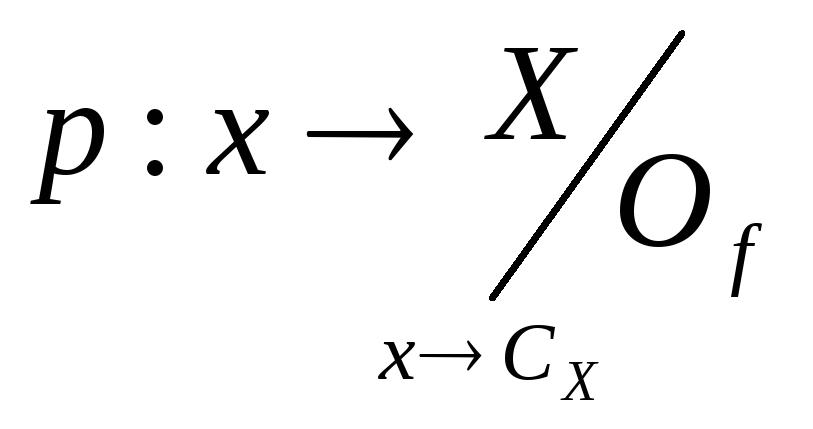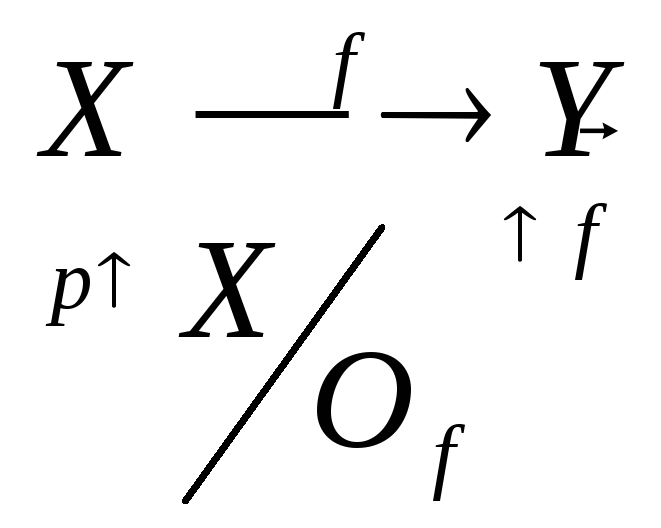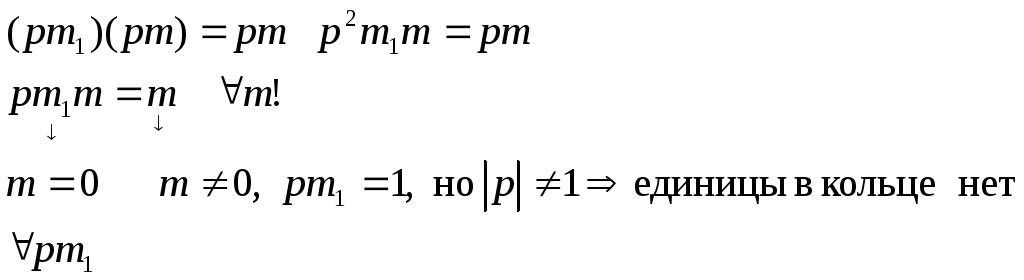Шпоры по дискре (2 семестр)
.doc|
1. (1 из 1) Понятие множества. Операции над множествами. Примеры. |
2. (1 из 2) Отображения. Виды отображений. Ассоциативность композиции отображений. |
|
Опр: Мн-во – это совокупность некоторых объектов. Опр: 1). S T, т.е. sS, sT; 2). S=T, т.е. S T и T S; 3). - пустое мн-во; 4). S T={xxS и xT}; 5). S T={xxS xT}; 6). S\T={xxS xT}; 7). X*Y – декартово произведение – это новое множество, состоящме из: X*Y={(x,y)xX, yY}; 8). X – конечное множество и Х - количество элементов множества X (конечное). Пр.: X, Y – конечное, Х=n, Y=m; X*Y=nm. XY=n+m — XY.
|
Отображение: Опр1: f:XY – отображает с области знач. Y и области определения Х, если каждому элементу хХ поставлен в соответствие единственный элемент из множества Y – f(x); Опр2: Если Y=X, то f называется преобразованием множества Х; Опр3: Im (образ) f={f(x)xX} – образ множества Х при действ. отобр. f; f —1(y)={xXf(x)=y} – полный прообраз элемента yY; Опр4: f: XY – сюрьективное (или отображение на), если Im f=Y, т.е. yY xX: f(x)=y;
Опр5: Отображение f: XY – инъективное (отображение в), если из xx` f(x)f(x`), x, x` X; Опр6: Отображение f: XY – биективное отображение, если f - сюрьективное и f – инъективное, т.е. взаимнооднозначное отображение.
Опр7: Отображение f:
XY
, g:
а).
б). xX, f(x)=g(x). Пример:
Опр8: eX: XX – единичное отображение на множествово Х, если xX, eX(x)=x.
|
|
2. (2 из 2) Отображения. Виды отображений. Ассоциативность композиции отображений. |
3. (1 из 1) Обратное отображение. Критерий обратимости отображения. |
|
Опр9: f: XY, g: X`Y. Если X` X, то g – ограничением f на Х` и f – продолжением g, если g(x)=f(x), xX`. Опр10: Произведение (композиция) отображение g: UV, f: VW называется fog: UW: fog(u)=f(g(u)) uU Утв: Композиция отображений – ассоциативно, т.е. если h:UV, g:VW, f:WT, то f(gh)=(fg)h. Доказательство: nU f(gh)(u)=f((gh)u)=f(g(h(u)))=fg(h(u))=((fg)h)(u). # Св-во: f: XX, g: XX. Композиция отображение вообще говоря не коммутативна, т.е. f*gg*f.
|
Определение: Обратные отображения.
Пусть
Утв: Обратное отображение единственное.
Док-во: От противного
Утв: Отображение
Док-во: Лемма 1: Если
а) Допустим, что
б)
Пусть
|
|
4. (1 из 1) Критерий обратимости отображения для случай конечного множества. |
5. (1 из 2) Бинарные отношения на множествах. Отношение эквивалентности. Примеры. |
||||||||||||||||
|
“ Т.к.
“ Следствие
1° Если
Следствие
2°
Утверждение. Если
Доказательство: Надо
показать, что
Т.к.
Пусть
Рассмотрим
|
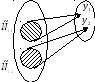
Определение: Множества X и Y имеют одинаковую мощность (или равномощны), если существует φ: X→Y такое, что φ-биективно. Множество М счетное, если М и N0 равномощны. Отношение на множестве. Определение: Пусть X,Y – множества. Всякое
Если
Х = Y, то O
- бинарное отношение на Х. Элемент х Пример:
“<” бинарное отношение на R,
такое, что
Пример:
1-a коорд.
Пример:
a b c a
b
c
Определение: Бинарное отношение “~” на множестве Х называется отношением эквивалентности, если:
|
|
5. (2 из 2) Бинарные отношения на множествах. Отношение эквивалентности. Примеры. |
6. (1 из 1) Разбиение множества и классы эквивалентности. |
||||||||||||||||||||||||||||||||
|
3)
Пример: 1. Выполняется. 2.
3.
Пример:
Т
a b c a
b
c
a b c a
b
c
|
Определение:
Множество
Свойства отношения эквивалентности.
1° Множество классов эквивалентности
по отношению “~” на множестве Х –
разбиение множества Х есть разбиение
множества
!
1)
2)
Док-во:
Допустим, что классы эквивалентности пересекаются:
Пример: a, b, c – множество {a}, {b,c}- классы эквивалентности {a, b, c} = X
X = {a}
|
|
7. (1 из 1) Основное свойство отношения эквивалентности. |
8. (1 из 1) Фактор-множество. Примеры. |
|
Свойство 2°
Пусть
Док-во: Рассмотрим
отношение
Покажем, что
а)
б)
в)
|
Определение
Разбиение множества X
соответствующее некоторому отношению
эквивалентности
Обозначается
Пример:
О
Можно
ввести:
Пример: Все студенты одинакового роста.
а) Доказано для
б) Для n студентов доказано. Докажем для n+1. Возьмем других n студентов:
|
|
9. (1 из 2) Алгебраические структуры- Определения и примеры полугрупп и моноидов. |
9. (2 из 2) Алгебраические структуры- Определения и примеры полугрупп и моноидов. |
|
Основные алгебраические структуры Определение:
n-арной операцией
на множестве A называется
любое отображение
Если n=2, то
n=1 – унарная операция
n=0 – считается, что Далее будем рассматривать бинарные операции. Определение:
Множество A с заданными
на нём бинарными
Далее будем рассматривать алгебры с 1 или 2мя бинарными операциями. Определение:
Бинарная операция “*” заданная на
множестве A ассоциативна,
если
Определение:
Определение: X(*) – полугруппа, если “*” – ассоциативно. X(*) – моноид, если 1) X(*) полугруппа 2)
Свойство:
Если в
Док-во:
Допустим
|
Пример:
“*” – коммутативна, не ассоциативно. 1)
2) |
|
10. (1 из 1) Определения и примеры групп. |
11. (1 из 1) Определения и примеры колец. |
|
|
Определение. Группой называется непустое множество А с бинарной алгебраической операцией (*) (будем называть умножением) такой, что выполняются следующие аксиомы: 1.
2.
3.
4.
Определение. Группа называется коммутативной, если выполняется аксиома коммутативности: 5.
Примеры групп. 1.
2.
3.
4.
|
Определение Кольцо – множество с двумя бинарными операциями К(+,*);
Если К(*) – моноид, то К(+,*) – кольцо с единицей
Если
Пример:
а)
б) ассоциативность. в)
Найдем единичный элемент в pZ
относительно «
|
|



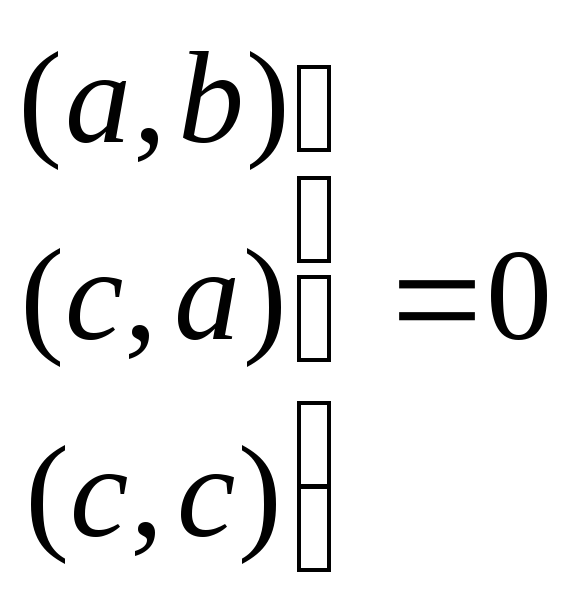 П
П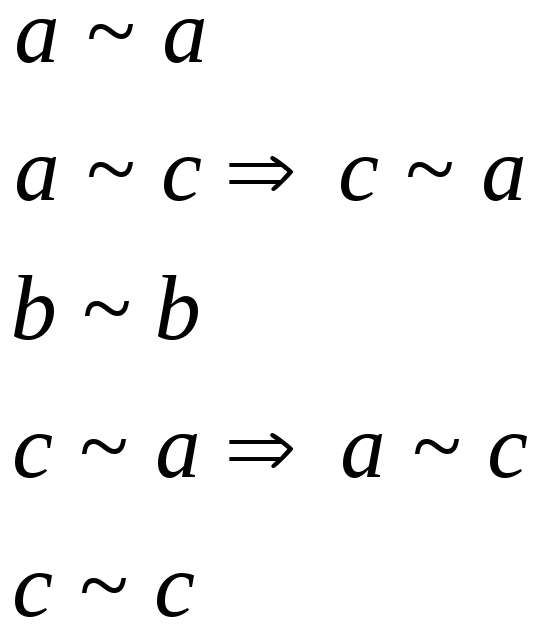
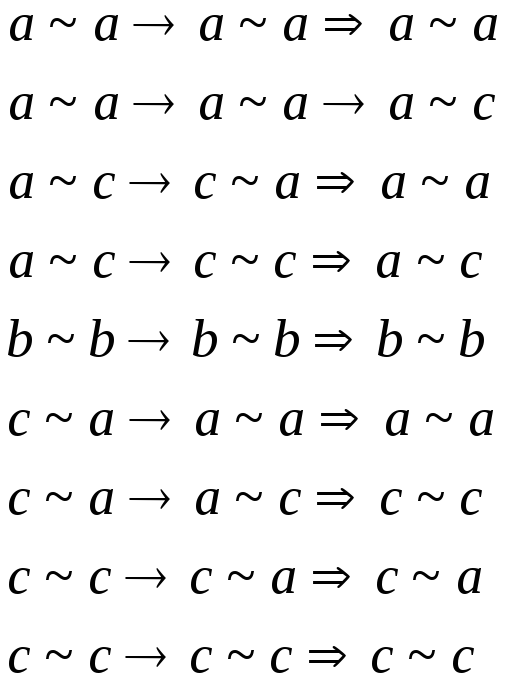
 чевидно,
что
чевидно,
что