Теоретическое распределение дискретной случайной величины

					…
					…

Таблица 2

Эмпирическое распределение дискретной случайной величины

x	0	1	2	3	4	5

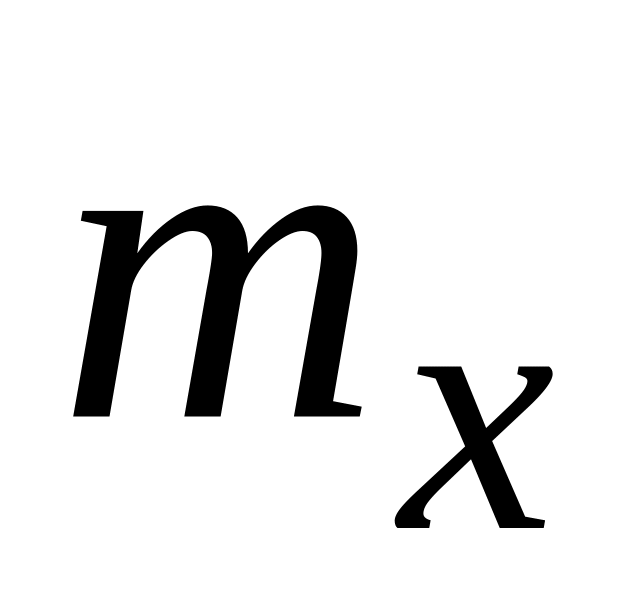
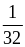
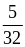
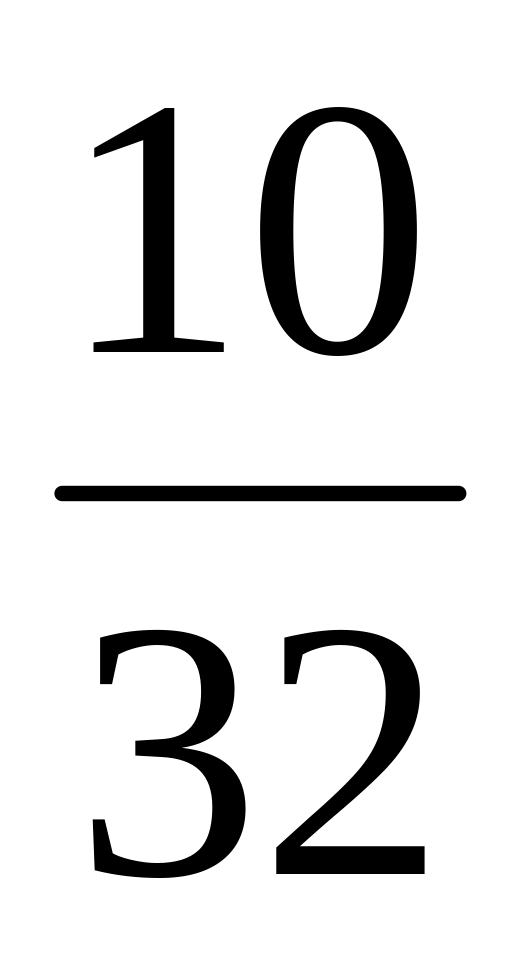
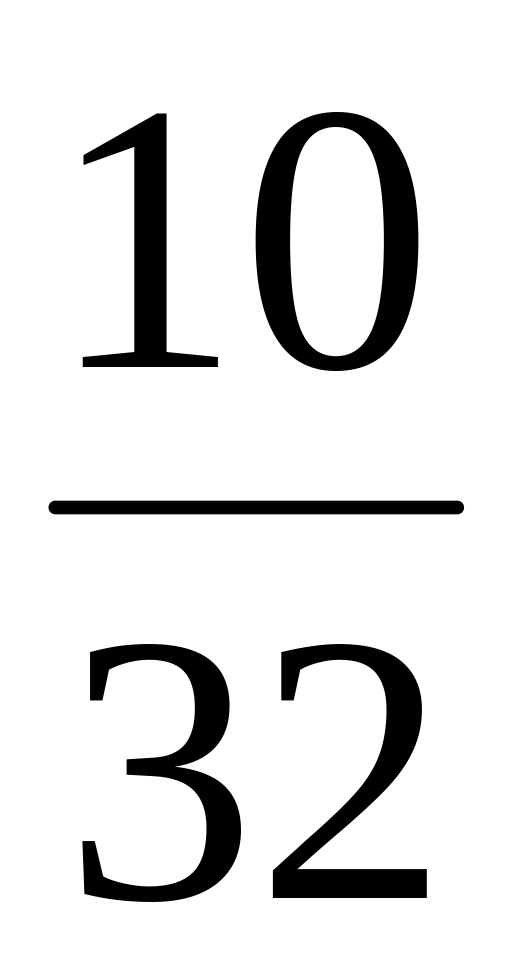
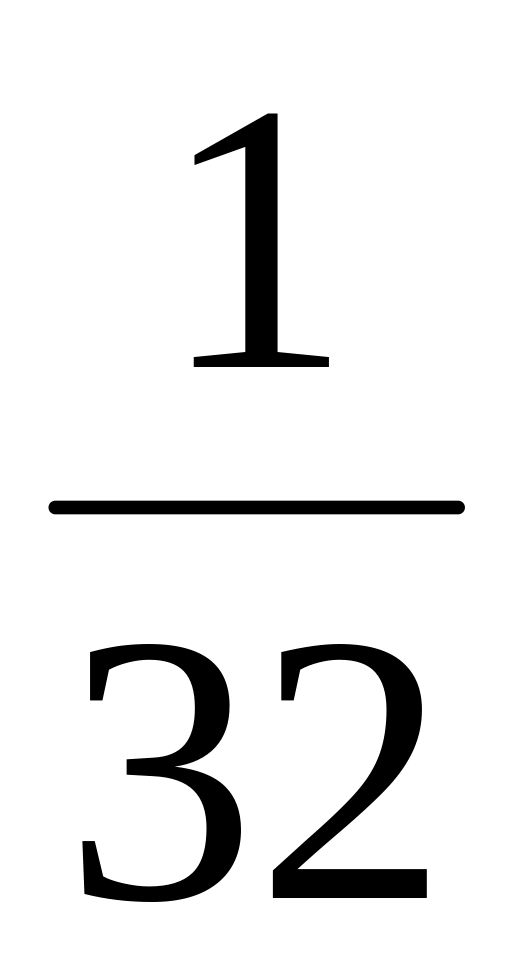
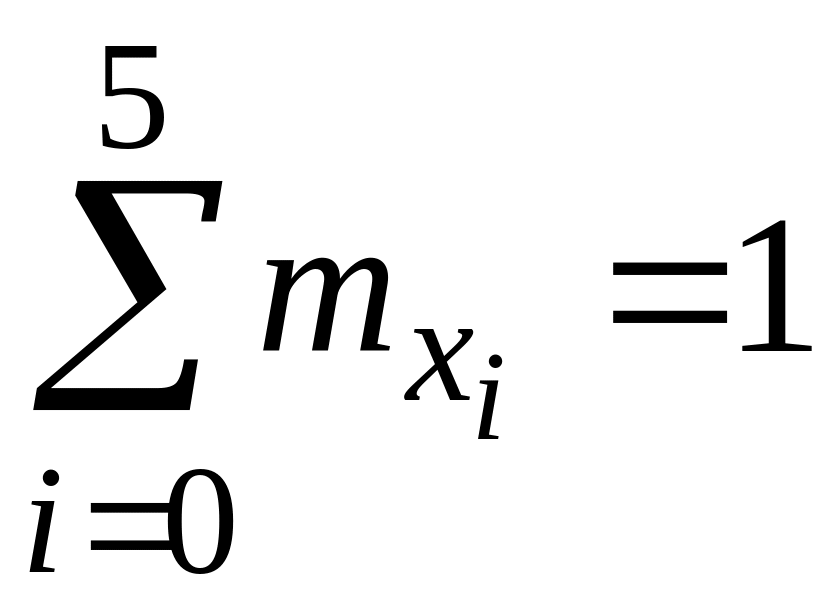
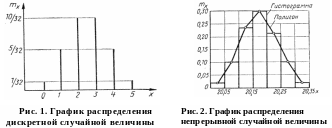
Если случайная величина является непрерывной, то возникает затруднение представить ее распределение в виде таблицы или графика, даже если значения случайной величины лежат в весьма узком интервале. Поэтому на практике при изучении случайных величин непрерывного типа их полученные значения разбивают на интервалы (разряды) с таким расчетом, чтобы величина интервала была несколько больше цены деления шкалы измерительного инструмента и таким образом компенсировалась бы погрешность измерений. Затем подсчитывают частоты не по действительным значениям случайной величины, а по интервалам, т. е. имеют дело не с частотами наблюденных значений случайной величины непрерывного типа, а с частотами значений их, лежащих в границах установленного интервала. Поэтому таблица эмпирического распределения случайной величины непрерывного типа будет иметь вид табл. 3.

Эмпирическое распределение случайной величины непрерывного типа (см. табл. 3) может быть представлено в виде ступенчатого графика или в виде ломаной кривой (рис. 2). Ступенчатый график называется гистограммой распределения, а ломаная кривая — полигоном распределения или эмпирической кривой распределения.

Таблица 3

Эмпирическое распределение случайной величины непрерывного типа

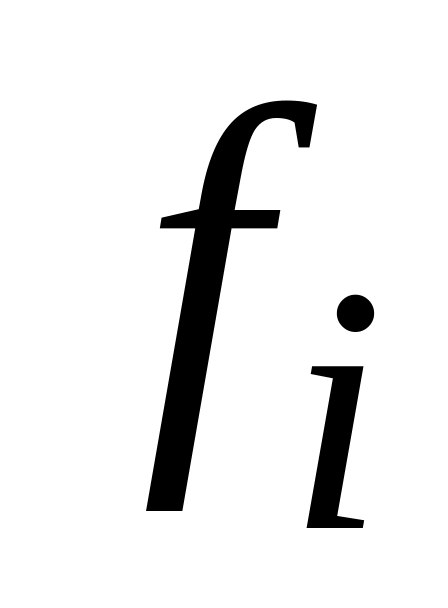
Интервалы значений x	Частота	Частость
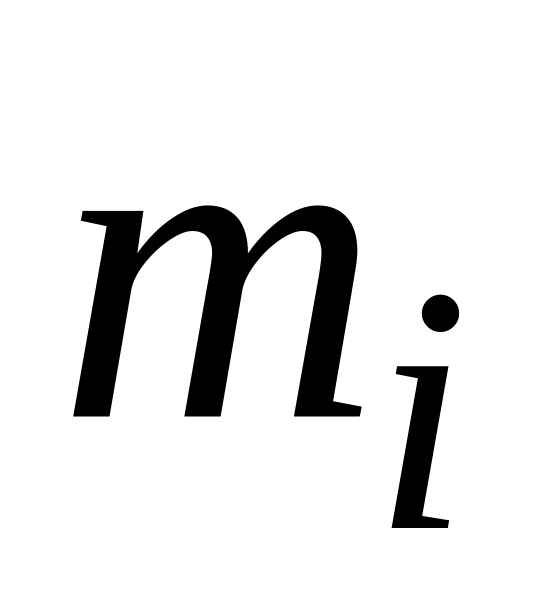
20—20,05	2	0,02
20,05—20,10	10	0,10
20,10—20,15	24	0,24
20,15—20,20	30	0,30
20,20—20,25	22	0,22
20,25—20,30	10	0,10
20,30—20,35	2	0,02

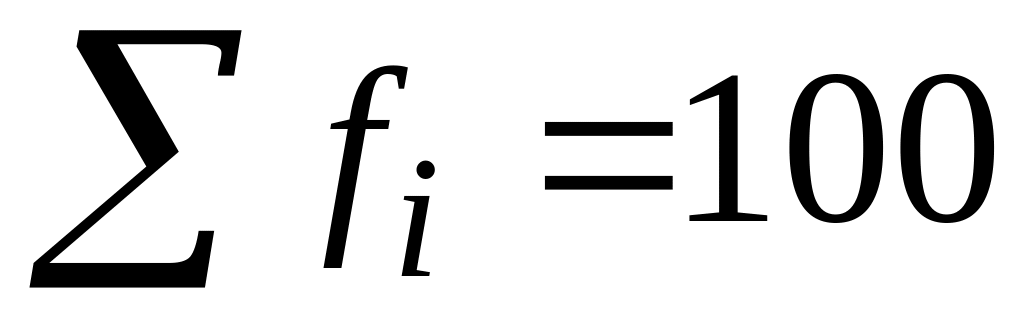
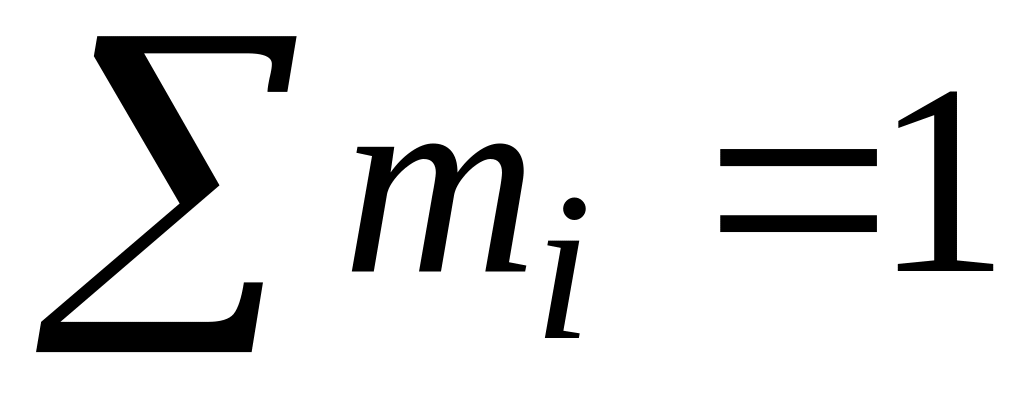
При изучении случайных величин непрерывного типа пользуются понятием функции распределения.

Пусть X — случайная величина, а х — какое-либо действительное число: при этом X < х и этому событию отвечает вероятность Р(X < х), которая, очевидно, является функцией х, т. е.

Р(X < х) = F(х).

F(х) называется функцией распределения вероятностей случайной величины или интегральной функцией распределения. Таким образом, интегральная функция распределения определяет вероятность того, что случайная величина X при испытаниях примет значение меньше произвольно изменяемого действительного числа х (- ∞ < х < + ∞). Случайная величина считается заданной, если известна ее функция распределения.

Для дискретной случайной величины интегральная функция распределения F(х) легко определяется по таблице или графику распределения. Например, по графику (см. рис. 1) F(х) для любого значения х равна сумме вероятностей тех значений X, которые лежат левее точки х. В частности, для X < 3:

F(3) = Р(Х<3) = Р(х=0) + Р(х= 1) + Р (х = 2) = .

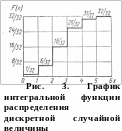
Интегральную функцию распределения можно представить в виде графика, если по оси абсцисс откладывать значения х, а по оси ординат — значения F(х) = Р(X < х). Для дискретной случайной величины график интегральной функции распределения будет иметь вид ступенчатой кривой. Для распределения согласно табл. 2 этот график будет иметь вид, изображенный на рис. 3. Ординаты кривой для любого значения х будут представлять сумму вероятностей предшествующих значений

F(х) = Р(X < х).

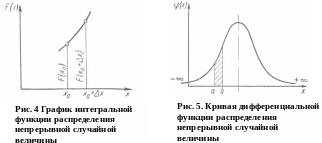
Для непрерывной случайной величины график интегральной функции распределения будет иметь вид не ступенчатой, а монотонно возрастающей кривой, имеющей касательную к каждой точке (рис. 4).

Интегральная функция распределения F(х) непрерывной случайной величины является дифференцируемой функцией. Первая производная от интегральной функции называется дифференциальной функцией распределения, или плотностью вероятности. Обозначим ее через φ(x). Тогда, исходя из определения производной, можно, написать

или, учитывая что F(х₀ + Δx) - F(х₀) = P(x₀ ≤ X < х₀ + Δx)

.

Таким образом, плотность вероятности φ(x) есть предел отношения вероятности того, что случайная величина X при испытаниях примет значение, лежащее в границах от х₀ до х₀ + Δx к величине интервала Δx, когда величина Δx стремится к нулю. F(х) является первообразной функцией по отношению к φ(x), поэтому вероятность того, что случайная величина X при испытаниях примет значение, лежащее в границах от a до b, равна определенному интегралу в пределах от a до b от плотности вероятности φ(x):

.

Дифференциальную функцию распределения непрерывной случайной величины, можно выразить в виде кривой, имеющей ту или иную форму. Например, при выполнении определенных условий дифференциальная функция распределения φ(x) непрерывной случайной величины может иметь вид холмообразной кривой (рис. 5). В данном случае вероятность

будет представлять площадь криволинейной трапеции с основанием ab, ограниченной сверху дифференциальной кривой распределения. Это следует из геометрической интерпретации определенного интеграла. Очевидно, что если случайная величина X изменяется в пределах ±∞, то вероятность того, что она при испытании примет любое значение в интервале ±∞, равна 1, т. е.

.

При наличии тех или иных условий возникновения значений случайных величин их распределения могут подчиняться вполне определенным законам. Ниже приведены законы распределения случайных величин, рассматриваемых в теории вероятностей, имеющие наибольшее практическое применение в машиностроении.