Министерство высшего и среднего специального образования РСФСР

Пермский политехнический институт

Кафедра математического анализа

Утверждено

на заседании кафедры

28 Марта 1987 г.

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методическая разработка

для самостоятельной работы студентов

и задания для расчетно-графической работы

Часть 3

Пермь 1988

ПРОВЕРКА ПАРАМЕТРИЧЕСКИХ СТАТИСТИЧЕСКИХ ГИПОТЕЗ.

Результаты наблюдений над случайными величинами используются для проверки правильности предположений относительно распределения генеральной совокупности. Всякое предположение о значениях параметров распределения или о виде закона распределения наблюдаемой случайной величины называют статистической гипотезой. Гипотеза называется параметрической, если предположения касаются значений параметров распределения, и – непараметрической, если содержит предположения о виде закона распределения. Проверяемая гипотеза называется нулевой и обозначается Нₒ. Нулевые гипотезы обычно утверждают, что различия между сравниваемыми величинами (параметрами или функциями распределения) отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями выборки. Наряду с гипотезой Нₒ рассматривают одну из альтернативных гипотез H, конкурирующих с Нₒ в том смысле, что если нулевая гипотеза отвергается, то принимается альтернативная. Например, если проверяется гипотеза о равенстве параметра Θ некоторому значению Θₒ, т.е. Н: Θ = Θₒ, то в качестве альтернативной гипотезы можно рассмотреть одну из следующих:

H:Θ≠Θₒ ; : Θ>Θₒ ; : Θ<Θₒ ; : Θ=Θ (Θ≠Θₒ)

Выбор альтернативной гипотезы определяется конкретным содержанием задачи.

Задача статистической проверки гипотезы состоит в том, чтобы сформулировать такое правило, которое позволяло бы по результатам наблюдений принять или отклонить эту гипотезу. Правило, согласно которому проверяемая гипотеза Нₒ принимается или отвергается, называется статистическим критерием (или просто критерием) проверки гипотезы Нₒ. Так как решение принимается на основе выборки, необходимо выбрать подходящую выборочную статистику критерия, являющуюся функцией наблюдаемых значений, точное или приближенное распределение которой известно. При проверке простой параметрической гипотезы (гипотезы, содержащей предположение об одном значении параметра) в качестве статистики критерия выбирают ту же статистику, что и для оценки этого параметра

Пусть для проверки некоторой нулевой гипотезы Нₒ относительно параметра распределения служит выборочная статистика К. Предположим, что плотность распределения вероятностей выборочной статистики К при условии справедливости проверяемой гипотезы Нₒ равна , и имеет вид, изображенный на рисунке, а математическое ожидание статистики равно Кₒ. Тогда вероятность того, что случайная величина К попадет в произвольный интервал , можно найти по формуле: .

З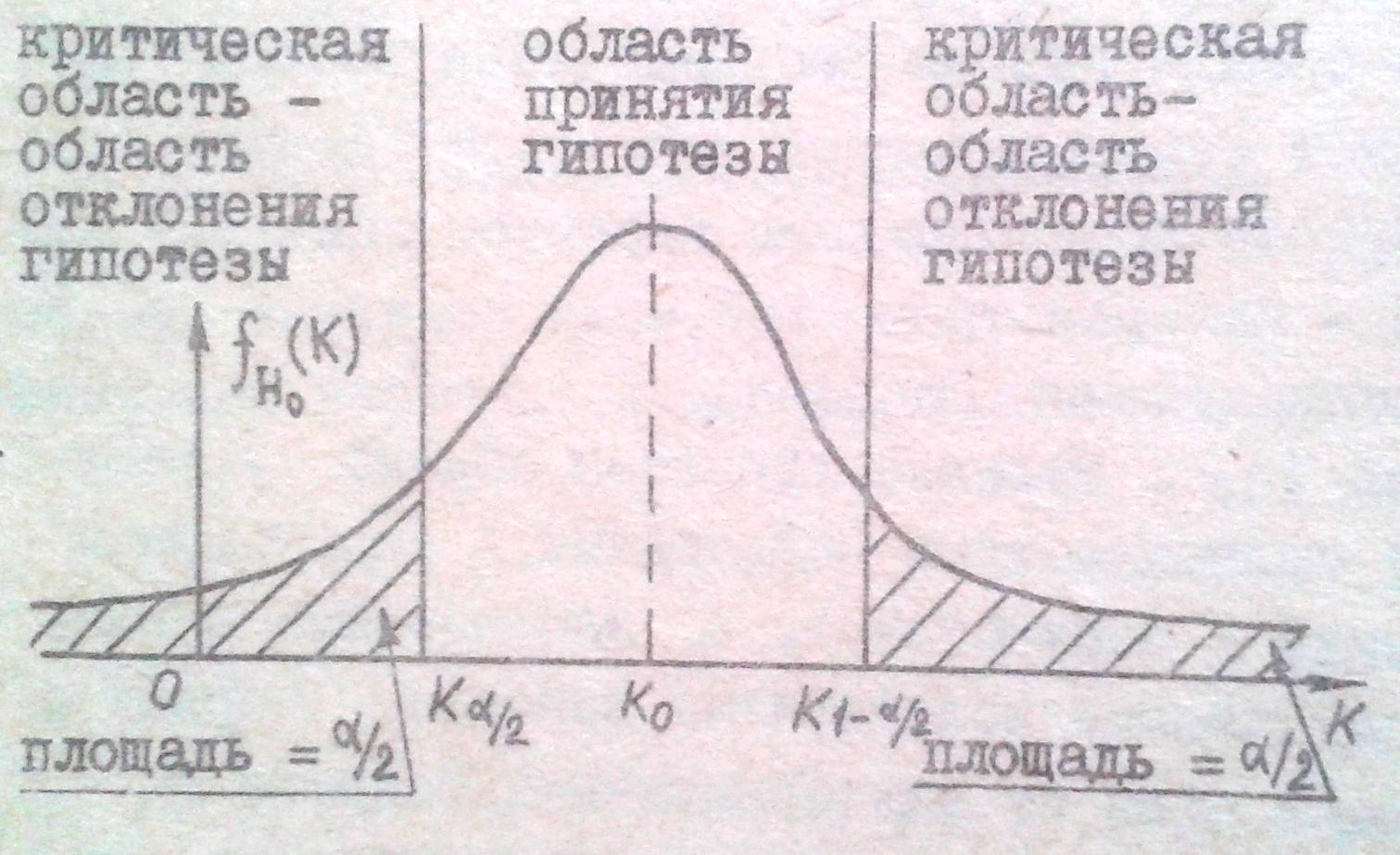ададим эту вероятность равной и вычислим квантили К-распределения и :

,

.

Следовательно, вероятность того, что случайная величина будет находится внутри интервала , равна , а вероятность того, что она окажется вне этого интервала, равна.

Зададим вероятность настолько малой, чтобы попадание К за пределы интервала можно было считать маловероятным событием. Тогда, из принципа практической невозможности маловероятных событий, можно считать, что если нулевая гипотеза справедлива, то при проверки ее с помощью критерия К наблюдаемое его значение (вычисленное по данным выборки), должно обязательно попасть внутрь интервала . Поэтому этот интервал называют областью допустимых значений критерия, при которых нулевая гипотеза не отклоняется, или областью согласия с гипотезой.

Если же наблюдаемое значение критерия К попадет за пределы рассматриваемого интервала, то это означает, что произошло маловероятное событие, т.е. что проверяемая нулевая гипотеза с вероятностью неверна. В связи с этим, области: и называются областями отклонения проверяемой нулевой гипотезы или критической областью критерия К.

Вероятность называют уровнем значимости. Уровень значимости определяет «размер» критической области. Положение критической области на множестве значений статистики К зависит от формулировки альтернативной гипотезы H. Например, если проверяется гипотеза Нₒ: Θ = Θₒ, а альтернативная гипотеза формулируется как H:Θ>Θₒ (Θ<Θₒ), то критическая область располагается справа (слева) от математического ожидания Кₒ статистики К и называется односторонней (см. рисунок). В этом случае критерий К также называется односторонним (правосторонним или левосторонним). Если альтернативная гипотеза формулируется как H:Θ≠Θₒ , то критическая область размещается по обе стороны от Кₒ и называется двусторонней. Соответственно и критерий К в этом случае называют двусторонним.

Квантили и в этих случаях определяются из условий:

и

.

Таким образом, проверка параметрической статистической гипотезы при помощи критерия значимости (критерия, основанного на использовании заранее заданного уровня значимости) может быть разбита на следующие этапы:

1. Формулировка проверяемой (Нₒ) и альтернативной (H) гипотез;

2. Назначение уровня значимости ;

3. Выбор статистики критерия для проверки гипотезы Нₒ;

4. Определение закона распределения статистики при условии справедливости гипотезы Нₒ;

5. Определение вида критической области (одно- или двусторонняя);

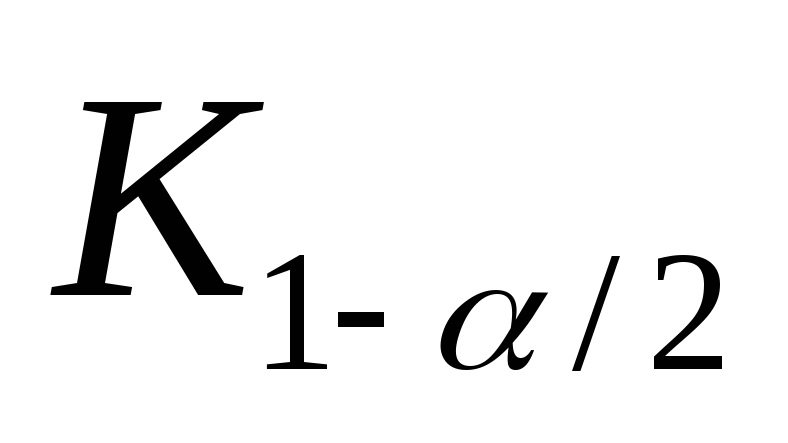6. Нахождение квантилей и или , 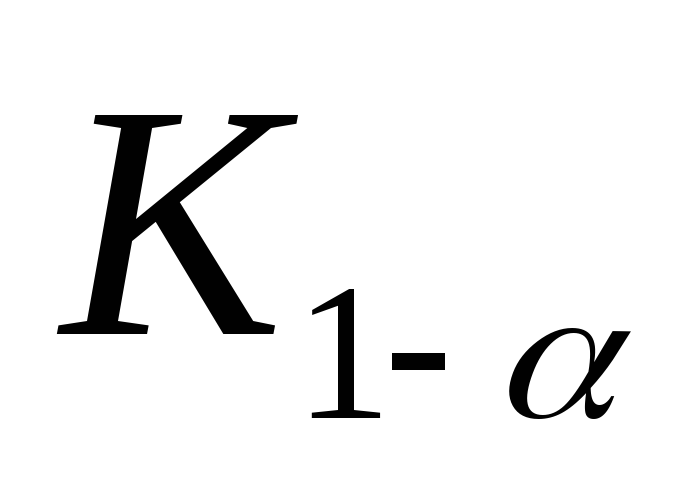в зависимости от вида критической области;

7. Вычисление выборочного значения статистики критерия по данным выборки;

8. Принятие решения о согласии опытных данных с нулевой гипотезой и принятия ее или об отклонении выдвинутой гипотезы.

Пример 1. Техническая норма предусматривает в среднем 40 с. На выполнение определенной технической операции, поступили сигналы, что они в действительности затрачивают на эту операцию больше времени. Для проверки произведены измерения времени выполнения этой технической операции у 16 работниц т получены следующие результаты:

с.(среднее время заполнения операции);

.

Можно ли по имеющимся хронометрическим данным на уровне значимости отклонить гипотезу о том, что действительно среднее время исполнения этой технической операции соответствует норме?

Решение. Из условия следует, что нам надо проверить нулевую гипотезу Нₒ:m=40 с. (техническая норма установлена верно) против альтернативной гипотезы H:m > 40 с. (техническая норма установлена неверно). Для проверки данной нулевой гипотезы применим t-критерий значимости с правосторонней критической областью.

Вычислим наблюдаемое значение t-критерия.

По таблице квантилей распределения Стьюдента по уровню значимости и числу степеней свободы находим значение , удовлетворяющее условию . Это значение .

Так как , то нет оснований для отклонения нулевой гипотезы (пересмотра технической нормы времени исполнения данной операции). Таким образом, мы доказали, что разность между средним временем (по хронометражу), затрачиваемым на данную техническую операцию, и нормой времени существенно незначима (случайна).

Пример 2. Выборка 50 электроламп завода А показала среднюю продолжительность работы ч. со средним квадратическим отклонением 80 ч, а такая же по объему выборка того же типа ламп завода ч со средним квадратическим отклонением 994 ч. Проверить гипотезу о том, что эти заводы выпускают лампы одинакового качества (средний срок службы лам обоих заводов одинаков). Уровень значимости принять равным 0,05.

Решение. Так как объемы выборок достаточно велики, то предложив, что продолжительность работы электроламп, выпускаемых заводами А и Б, являются случайными величинами, имеющими нормальное распределение: и , причем , а и неизвестны. Согласно условию, нам необходимо проверить нулевую гипотезу Нₒ:=(средний срок службы ламп, выпускаемых заводами А и Б, одинаков) против альтернативной гипотезы H:>(лампы, выпускаемые заводом А, имеют большой срок службы).

Для проверки нулевой гипотезы применим правосторонний u-критерий. Вычислим наблюдаемое значение статистики

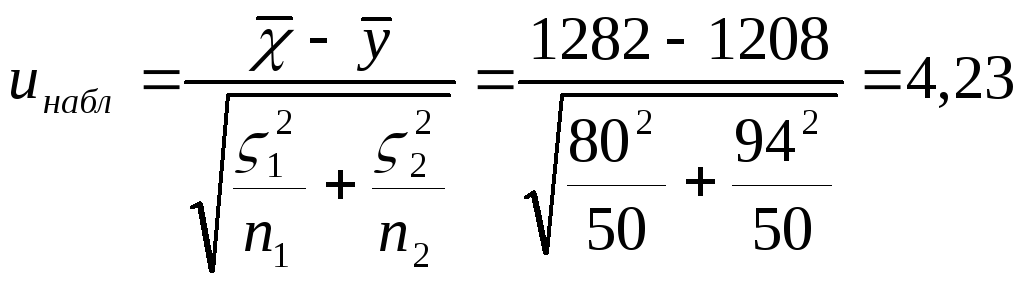
По таблице значений функции Лапласа найдем критическую точку (квантиль) , удовлетворяющую условию

. Это значение равно 1,64. Так как , то нулевая гипотеза отклоняется в пользу альтернативной. Другими словами, считается «статистически доказанным», что срок службы ламп, выпускаемых заводом А, больше срока службы ламп, выпускаемых заводом Б.

Пример 3. Точность работы станка-автомата проверяется по дисперсии контролируемого размера деталей, которая не должна превышать . Взята проба из 11 случайно отобранных деталей, и получены следующие результаты (в миллиметрах): 100,6; 99,6; 100,0; 100,1; 100,3; 100,0; 99,9; 100,2; 100,4; 100,6; 100,5. На основании имеющихся данных проверить, обеспечивает ли станок заданную точность. Уровень значимости принять равным 0,05.

Решение. Из условия следует, что нам необходимо проверить нулевую гипотезу (станок обеспечивает заданную точность) против альтернативной гипотезы (станок не обеспечивает заданную точность). Альтернативная гипотеза сформулирована в виде , так как мы не считаем . Если в действительности т окажется, что , то это означает, что станок хорошо налажен и выпускает детали более высокого качества, чем предполагалось.

Найдем точечные оценки параметров нормального закона:

Для проверки нулевой гипотезы применим критерий с правосторонней критической областью. Вычислим наблюдаемое значение тестовой статистики:

.

По таблицам квантилей -распределения по заданному уровню значимости и числу степеней свободы находим критическую точку , удовлетворяющую условию . Это значение равно 18,307.

Так как , нулевая гипотеза отклоняется в пользу альтернативной. Это значит, что станок не обеспечивает заданной точности и требует подналадки.

Пример 4. Двумя методами произведены измерения одной и той же физической величины. Первым методом эта величина измерялась 10 раз. Получены следующие результаты:

.

Вторым методом эта же величина измерялась 8 раз. Получены следующие результаты:

.

М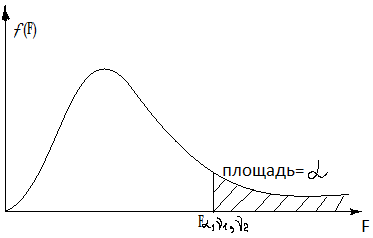ожно ли считать, что оба метода обеспечивают одинаковую точность. Уровень значимости принять . Предполагается, что результаты измерений распределены нормально и выборки независимы

Решение. Из условия следует, что нам необходимо проверить нулевую гипотезу (оба метода обеспечивают одинаковую точность) против альтернативной гипотезы (второй метод измерения обеспечивает более высокую точность).

Вычислим наблюдаемые значения F-критерия:

,

По таблице квантилей F-распределения по уровню значимости и числу степеней свободы и находим критическую точку .

Так как, то нет основания для отклонения нулевой гипотезы. Другими словами, имеющаяся информация о точности этих методов не дает основания считать, что второй метод измерения лучше первого.

ОШИБКИ, ДОПУСКАЕМЫЕ ПРИ ПРОВЕРКЕ СТАТИСТИЧЕСКИХ ГИПОТЕЗ.

При проверке статистических гипотез всегда существует риск принятия ложного решения. Пусть выборочное значение статистики попадет в критическую область и в соответствии с критерием гипотеза Нₒ отклоняется. Если тем не менее эта гипотеза верна, то принимаемое решение ошибочно. Ошибка, совершаемая при отклонении правильной нулевой гипотезы Нₒ называется ошибкой первого рода. Очевидно, вероятность допустить ошибку первого рода равна вероятности попадания статистики критерия в критическую область, т.е. равна уровню значимости .

Ошибка второго рода происходит в том случае, если гипотеза Нₒ принимается, но она неверна, а верна в действительности альтернативная гипотеза . Вероятность совершения ошибки второго рода принято обозначать и можно вычислить по формуле:

,

Если критерий К левосторонний. Геометрическая интерпретация ошибок первого и второго рода дана на рисунке:

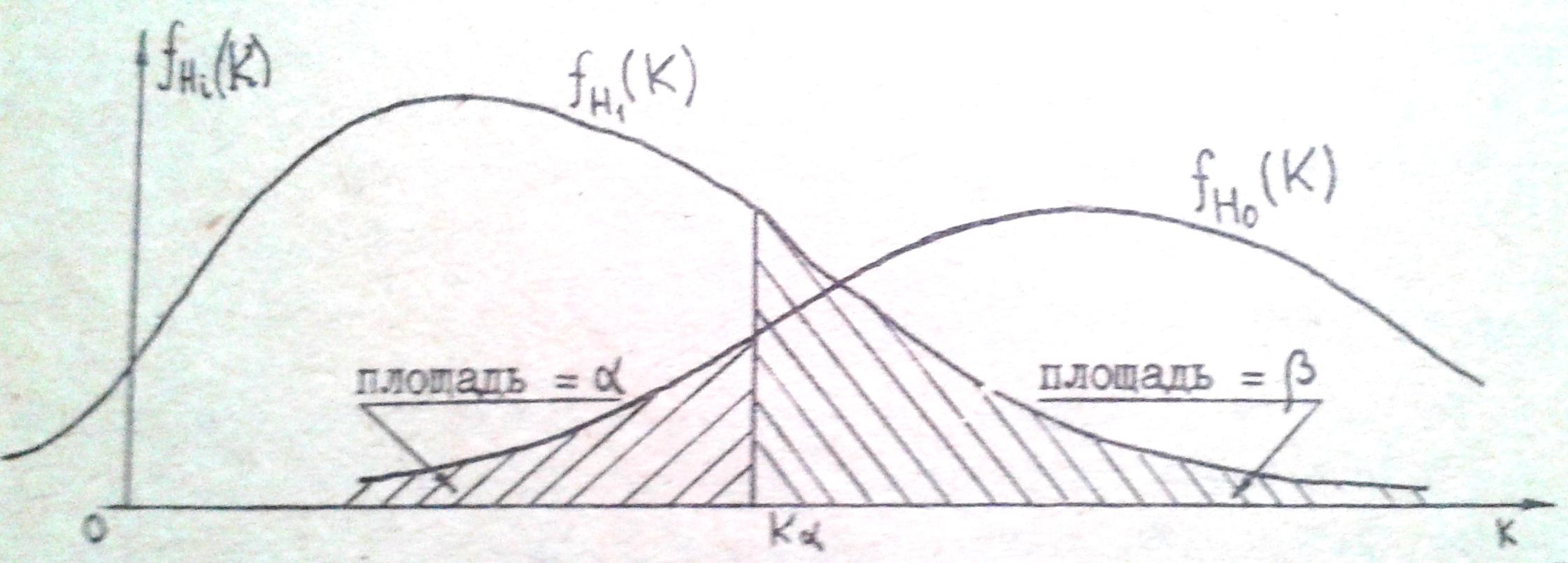
Из рисунка видно, что уменьшая вероятность совершения одной ощибки, мы тем самым увеличиваем вероятность другой ошибки. При этом выполняются следующие предельные соотношения:

, .

Доказательства этих соотношений мы не приводим. Первые два равенства говорят о том, что статистические доказательства истинности гипотез и становятся достоверными только при бесконечно большом объеме выборки и единственным способом одновременного уменьшения вероятностей ошибок первого и второго рода является увеличение объема выборки. Последнее равенство говорит о том, что уменьшая вероятность ошибки первого рода до нуля, мы при фиксированном объеме выборки допускаем неограниченный риск сделать ошибку второго рода.

Как же следует выбирать уровень значимости статистических критериев? Ответ на этот вопрос зависит от потерь, вызываемых ошибками первого и второго рода. Если совершение ошибки первого рода приведет к большим потерям по сравнению с потерями, вызываемыми совершением ошибки второго рода, то следует принят по возможности меньшее значение . При этом нельзя выбирать , так как будут приниматься все нулевые гипотезы, в том числе и неправильные, т.е. с практической достоверностью будут допускаться ошибки второго рода.

Рассматриваемые здесь критерии значимости – это односторонние действующие критерии, так как с их помощью принимается (с заранее фиксированным риском) только одно решение: «Отклонить проверяемую нулевую гипотез». Если же нет оснований отклонить нулевую гипотезу данным критериям, то утверждается, что данные выборки не противоречат выдвинутой гипотезе (согласуются с ней). Статистические критерии значимости не позволяют принять решение: «Нулевая гипотеза является правильно», так как при применении указанных критериев вероятность принятия ложной нулевой гипотезы остается неизвестной.

Практик-экспериментатор, как правильно, хочет проверить, дают ли результаты эксперимента право отклонить нулевую гипотезу, с тем чтобы принять вместо нее альтернативную, которую он отстаивает (новая технология производства, усовершенствование некоторого узла и т.д.). Доказательство истинности нулевой гипотезы (например, подтверждения эффективности старой технологий) его не интересует. Поэтому в большинстве случаев для практических приложений достаточно статистических критериев значимости, позволяющих только отклонять выдвинутую нулевую гипотезу с фиксированной малой вероятностью отклонить верную гипотезу.

Выбор уровня значимости до некоторой степени произволен. Стало обычным выбирать в качестве одно из стандартных значений: 0,005; 0,01; 0,05; 0,10; это, однако, не означает, что нельзя выбирать, например, . Принятая стандартизация позволяет сократить объем таблиц критических значений (квантилей) статистических критериев.

Необходимо учитывать такие, что чем меньше значимости , тем труднее отклонить нулевую гипотезу. Поэтому не следует стремиться выбирать уровень значимости слишком малым.