- •1.Финитные функции.
- •2. Свертка финитных функций
- •3. Линейные операторы и функционалы в пространстве финитных функций.
- •4.Определение обобщенной функции. Примеры обобщенных функций.
- •5.Определение обобщенной функции. Алгебраические действия над обобщенными функциями.
- •6.Дифференцирование обобщенных ф-ций
- •7.Интегрирование обобщенных функций.
- •8. Носители обобщенных функций.
- •9. Нелинейные эволюционные операторы с обобщенными импульсными характеристиками: основные определения и свойства.
- •11. Композиция эволюционных операторов
- •12.Композиция эволюционных операторов Вольтерра-Винера.
- •13.Нелинейные эволюционные операторы с обобщенными спектральными характеристиками: основные пространства, обобщенное преобразование Лапласа.
- •14.Квазиобращение эволюционных операторов с обобщенными спектральными характеристиками.
11. Композиция эволюционных операторов
Пусть
А и В – эволюционные операторы кратностей
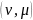 и
и
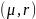 соответственно:
соответственно:
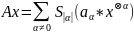 ,
,
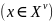 ,
,
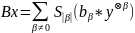 ,
,
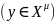 .
.
Рассмотрим композицию операторов B○A:
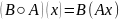 ,
.
,
.
Теорема (о композиции эволюционных операторов).
Композиция
С= B○A
эволюционных операторов В и А кратностей
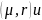 соответственно, где
соответственно, где
, ,
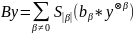 ,
.
,
.
является эволюционным оператором
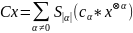 ,
,
,
,
импульсные характеристики вычисляются по формуле
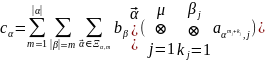
Следствие
1 (когда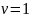 ).
).
Композиция
С= B○A
эволюционных операторов В и А кратностей
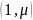 соответственно, где
соответственно, где
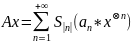 ,
,
 ,
,
, .
является эволюционным оператором
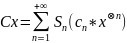 ,
,
,
,
импульсные характеристики которого вычисляются по формуле
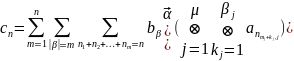 (
),
(
),
Где
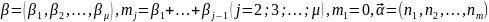 ,
,
 j-ая
j-ая
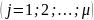 компонента импульсной характеристики
компонента импульсной характеристики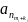
Следствие
2 (когда
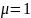 )
)
Композиция
С= B○A
эволюционных операторов В и А кратностей
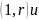
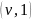 соответственно, где
соответственно, где
, ,
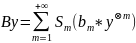 ,
,
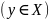 .
.
является эволюционным оператором
, ,
импульсные характеристики вычисляются по формуле
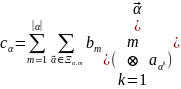
Следствие
3 (когда и
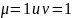 ,
получаем следствие о композиции
эволюционного оператора порядка
,
получаем следствие о композиции
эволюционного оператора порядка
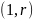 и оператора Вольтера-Винера ).
и оператора Вольтера-Винера ).
Композиция
С= B○A
эволюционных оператора В порядка
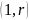
,
и оператора Вольтера-Винера А
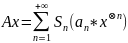 ,
,
,
,
является эволюционным оператором
, ,
импульсные характеристики которого вычисляются по формуле
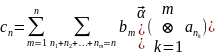 (
),
где
(
),
где
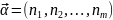 .
(1)
.
(1)
12.Композиция эволюционных операторов Вольтерра-Винера.
Пусть А и В – эволюционные операторы кратностей и соответственно:
, ,
, . Рассмотрим композицию операторов B○A:
, .Причём y=Ax.
Теорема(о композиции эволюционных операторов).
Композиция
С=B○A
эволюционных операторов В и А кратностей
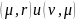 соответственно,
где
соответственно,
где
, ,
, .
является эволюционным оператором
, ,
импульсные характеристики вычисляются по формуле
Теорема (о композиции эволюционных операторов Вольтера-Виннера) Композиция С=B○Aоператоров Вольтера-Винера В и А:
, ,
,
является оператором Вольтера-Винера
, ,
импульсные характеристики которого вычисляются по формуле :
( ), где .
13.Нелинейные эволюционные операторы с обобщенными спектральными характеристиками: основные пространства, обобщенное преобразование Лапласа.
Пусть
принадлежит пространству
.
Через
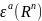 обозначается совокупность всех бесконечно
дифференцируемых функций φ
на пространстве Rn,
удовлетворяющих условию:
обозначается совокупность всех бесконечно
дифференцируемых функций φ
на пространстве Rn,
удовлетворяющих условию:
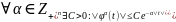
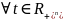 ,
,
где |t| = t1 + t2 + … + tn.
Рассмотрим
тензорное
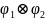 произведение функций
произведение функций
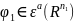 и
и
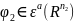
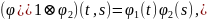 где
где
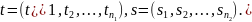
Объединим
пространства
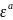 (Rn)
с условием, что a
< c
(R),
т.е.
(Rn)
с условием, что a
< c
(R),
т.е.
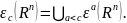 Обозначим полученную совокупность
через
Обозначим полученную совокупность
через
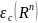 .
.
Определение.
Обобщенной функцией экспоненциального
роста на Rn
степени с
(c
из Rn)
называется любой нелинейный непрерывный
функционал на пространстве
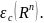
Определение.
Преобразованием Лапласа обобщенной
функции называется функция
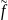 ,
определяемая на множестве
,
определяемая на множестве
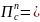 равенством
равенством
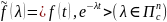 (1)
(1)
где
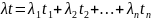 .
.
Так
как функция
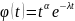 принадлежит пространству
для любого
принадлежит пространству
для любого
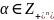 , то из (1) следует, что
, то из (1) следует, что
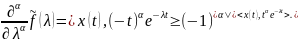
Примеры преобразований Лапласа от некоторых функций.
Пример 1. Пусть f = θ – функция Хевисайда. Тогда имеем:
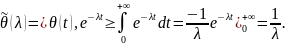
Пример
2. Пусть f
= δ – дельта-функция. Тогда имеем:
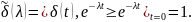
Рассмотрим свойства преобразований Лапласа.
1.Преобразование
Лапласа от производных обобщенной
функции имеет вид:
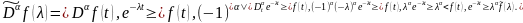
2.
Преобразование Лапласа тензорного
произведения обобщенных функций
вычисляется по формуле

3. Преобразование Лапласа свертки обобщенных функций будет равно