
- •1.Финитные функции.
- •2. Свертка финитных функций
- •3. Линейные операторы и функционалы в пространстве финитных функций.
- •4.Определение обобщенной функции. Примеры обобщенных функций.
- •5.Определение обобщенной функции. Алгебраические действия над обобщенными функциями.
- •6.Дифференцирование обобщенных ф-ций
- •7.Интегрирование обобщенных функций.
- •8. Носители обобщенных функций.
- •9. Нелинейные эволюционные операторы с обобщенными импульсными характеристиками: основные определения и свойства.
- •11. Композиция эволюционных операторов
- •12.Композиция эволюционных операторов Вольтерра-Винера.
- •13.Нелинейные эволюционные операторы с обобщенными спектральными характеристиками: основные пространства, обобщенное преобразование Лапласа.
- •14.Квазиобращение эволюционных операторов с обобщенными спектральными характеристиками.
5.Определение обобщенной функции. Алгебраические действия над обобщенными функциями.
Пусть – пр-во финитных функций.
Опр. Линейный непрерывный функционал на пр-ве наз. обобщенной функцией (на числовой оси ).
– пр-во обобщенных функций (сопряженное к ).
Число
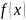 наз. значением обобщенной ф-ции
на финитной ф-циии
наз. значением обобщенной ф-ции
на финитной ф-циии
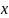 , и обознач.:
, и обознач.:
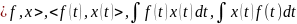
В пр-ве определены операции сложения и умножения на число:
1)
Если
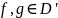 ,
то
,
то
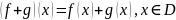
2)
Если
–
число и
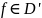 ,
то
,
то
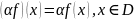
Док-ва, что так
определенные функционалы
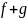 и
и
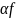 линейны и непрерывны в пр-ве
,
т.е. явл. обобщенными ф-циями, легко
следуют из определений.
линейны и непрерывны в пр-ве
,
т.е. явл. обобщенными ф-циями, легко
следуют из определений.
Из последнего
рав-ва следует :
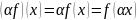 .
.
Так, если
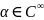 и
- обобщенная ф-ция, то
и
- обобщенная ф-ция, то
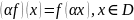 (1)
(1)
Т.к. произведение бесконечно дифференцируемой ф-ции на финитную ф-цию явл. финитной ф-цией, то рав-во (1) корректно. Докажем, что оно определяет обобщенную ф-цию . Т.к. – обобщенная ф-ция, то
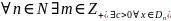 :
:
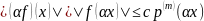 ,
(2)
,
(2)
где
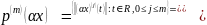
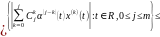
 .
.
Подставляя это
нер-во в (2) получим,
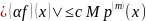
Отсюда следует, что – обобщенная ф-ция.
3)
Рассмотрим
операцию замены переменной. Пусть
 – биективная бесконечно дифференцируемая
ф-ция на числовой прямой. Если
– непрерывная ф-ция на числовой прямой,
то для
– биективная бесконечно дифференцируемая
ф-ция на числовой прямой. Если
– непрерывная ф-ция на числовой прямой,
то для
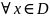 имеем:
имеем:
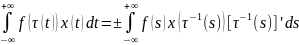 (3)
(3)
где берется знак
+, если
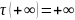 ,
и знак -, если
,
и знак -, если
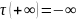 .
Обозначим
.
Обозначим
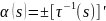 .
.
Тогда (3):
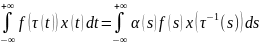
Если
– регулярная обобщенная ф-ция, порожденная
ф-цией
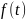 ,
а
,
а
 – регулярная обобщенная ф-ция, порожденная
ф-цией
– регулярная обобщенная ф-ция, порожденная
ф-цией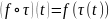 (
(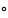 - операция композиции), то получим
- операция композиции), то получим
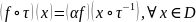 (4)
(4)
Так, композицией
обобщенной ф-ции
и
биективной ф-ции
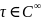 (бесконечно
дифференцируемая)
наз. обобщенная ф-ция
,
которая удовлетворяет соотношению (4).
(бесконечно
дифференцируемая)
наз. обобщенная ф-ция
,
которая удовлетворяет соотношению (4).
Обобщенная ф-ция
обозначается также
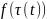 ,
а про ф-цию
,
а про ф-цию
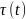 говорят, что она осуществляет замену
аргумента в обобщенной ф-ции
.
говорят, что она осуществляет замену
аргумента в обобщенной ф-ции
.
6.Дифференцирование обобщенных ф-ций
Одной из наиболее важнейших операций над обобщенными ф-ми явл операция дифф-ния.
Пусть f
– регулярная обобщённая ф-ция, порожденная
непрерывно дифференцируемой на числовой
оси функцией f(t).
Тогда
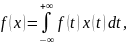
 .
Применяя ф-лу интегрирования по частям,
получим:
.
Применяя ф-лу интегрирования по частям,
получим:
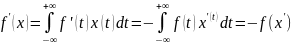 ,
.
,
.
Опр.
Производной
обобщённой ф-ции f
называется обобщенная функция
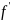 ,
определяемая равенством
,
определяемая равенством
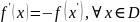 (1)
(1)
Понятие производной ф-ции определено для любой обобщённой ф-ции. Оператор дифферен-ния обобщенной ф-ций (D) – это оператор, сопоставляющий любой обоб. ф-ции ее производную. D – линейный оператор, обладает след. св-ми:
1.однородность:
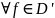 и
и
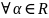
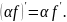
2.аддитивность:

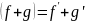 .
.
D – лин-ый оператор, действующий из про-ства в прос-во .
Cправедлива
cледующая
ф-ла
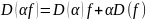 (2)
(2)
Д-во:
,
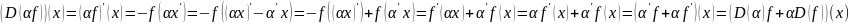
Примеры. 1) Пусть
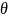 – регулярная обоб ф-ция, порожденная
ф-ей Хевисайда
– регулярная обоб ф-ция, порожденная
ф-ей Хевисайда
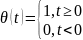 ,
тогда
,
тогда
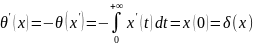 ,
т.е.
,
т.е.

2)sgn
– регулярная обоб ф-ция, порожденная
ф-ей
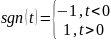 ,
,
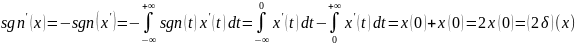 ,
т.е.
,
т.е.
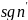 =
=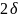 .
.
3)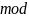 - регулярная обоб ф-ция, порожденная
ф-ей
- регулярная обоб ф-ция, порожденная
ф-ей
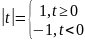 ,
тогда
,
тогда
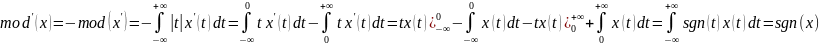 ,
т.е.
,
т.е.
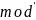 =
=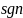 .
.
Опр.
Производной второго порядка обобщённой
ф-ии
наз обобщённая ф-ция
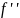 ,
являющаяся производной от производной
,
являющаяся производной от производной
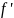 первого порядка обоб ф-ии
,
т.е.
первого порядка обоб ф-ии
,
т.е.
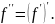
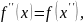 тогда
тогда
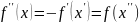 .
.
Пример.
из примера 2) и 3) =>
=
и
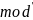 =
=> mod’’=(mod’)’=sgn’=2
.
Оператор, сопостовляющий любой обоб
ф-ии ее 2-ую производную, будем обозначать
=
=> mod’’=(mod’)’=sgn’=2
.
Оператор, сопостовляющий любой обоб
ф-ии ее 2-ую производную, будем обозначать
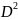
Опр.
Производной n-ого
порядка обобщённой ф-ции
наз обобщённая ф-ция
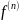 ,
явл производной от производной (n-1)-го
порядка
,
явл производной от производной (n-1)-го
порядка
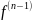 обобщённой ф-ции, т.е.
обобщённой ф-ции, т.е.
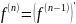 .
.
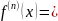 .
Линейный оперетор, сопост-ий обоб щённой
ф-ции ее n-ую
производную -
.
Линейный оперетор, сопост-ий обоб щённой
ф-ции ее n-ую
производную -
 .
.
