
- •1.Финитные функции.
- •2. Свертка финитных функций
- •3. Линейные операторы и функционалы в пространстве финитных функций.
- •4.Определение обобщенной функции. Примеры обобщенных функций.
- •5.Определение обобщенной функции. Алгебраические действия над обобщенными функциями.
- •6.Дифференцирование обобщенных ф-ций
- •7.Интегрирование обобщенных функций.
- •8. Носители обобщенных функций.
- •9. Нелинейные эволюционные операторы с обобщенными импульсными характеристиками: основные определения и свойства.
- •11. Композиция эволюционных операторов
- •12.Композиция эволюционных операторов Вольтерра-Винера.
- •13.Нелинейные эволюционные операторы с обобщенными спектральными характеристиками: основные пространства, обобщенное преобразование Лапласа.
- •14.Квазиобращение эволюционных операторов с обобщенными спектральными характеристиками.
9. Нелинейные эволюционные операторы с обобщенными импульсными характеристиками: основные определения и свойства.
Пусть
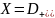 –
пр-во финитных слева бесконечно
дифференцируемых функции на числовой
оси. Зафиксируем натуральное число
–
пр-во финитных слева бесконечно
дифференцируемых функции на числовой
оси. Зафиксируем натуральное число
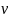 и рассмотрим
и рассмотрим
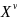 –
-cтепень
пр-ва
–
-cтепень
пр-ва
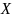 .
.
Обозначим через
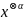 тензорную степень мультииндекса
тензорную степень мультииндекса
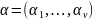 вектор-функций
вектор-функций
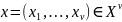 :
:
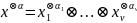
Пусть
и
 – натуральные числа,
– натуральные числа,
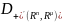 – пр-во всех обобщенных –мерных
вектор-функций на пр-ве
– пр-во всех обобщенных –мерных
вектор-функций на пр-ве
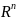 с носителем на
с носителем на
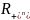 .
.
Пусть
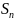 – оператор сокращения переменных
степени
:
– оператор сокращения переменных
степени
:
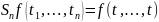 ,
где
–
-мерная
вектор-функция на пр-ве
.
,
где
–
-мерная
вектор-функция на пр-ве
.
Опр.
Эволюционным оператором кратности
 наз. оператор
наз. оператор
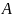 ,
действующий по формуле
,
действующий по формуле
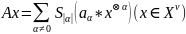
где суммирование
ведется по мультииндексам
не равным нулю,
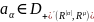 ,
-
,
-
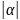 -мерная
свертка.
-мерная
свертка.
Опр. Эволюционный оператор кратности (1, 1) наз. оператором Вольтерра-Винера.
Опр.
Обобщенную вектор-функцию
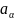 наз. импульсной характеристикой
мультииндекса
эволюц. оператора
.
наз. импульсной характеристикой
мультииндекса
эволюц. оператора
.
Опр.
Семейство
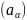 – семейством импульсных характеристик
оператора
.
– семейством импульсных характеристик
оператора
.
Опр.
Оператор
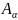 ,
определяемый рав-вом
,
определяемый рав-вом
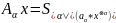 наз. –й компонентой
оператора
.
наз. –й компонентой
оператора
.
Опр. Если
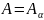 ,
то
наз. однородным
эволюционным оператором степени
.
,
то
наз. однородным
эволюционным оператором степени
.
Опр.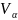 – мн-во эволюционных операторов степени
.
– мн-во эволюционных операторов степени
.
Св-ва оператора
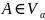 :
:
1)
Линейность и непрерывность относительно
-й тензорной степени: отображение
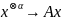 линейно и непрерывно.
линейно и непрерывно.
2)
Сохранение нуля:
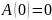
3)
Однородность степени
:
для
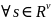 и
и
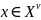 имеет место
рав-во
имеет место
рав-во
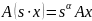 ,
,
где
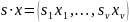 ,
,
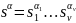
4)
Причинность: если
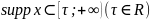 ,
то
,
то
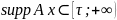
Опр.
Для любого фиксированного нат. числа
определим оператор
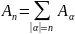 ,
который наз. однородной компонентой
–й степени эволюционного оператора
.
,
который наз. однородной компонентой
–й степени эволюционного оператора
.
Опр.
Оператор
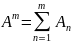 – наз. полиномиальной компонентой
степени
оператора
.
– наз. полиномиальной компонентой
степени
оператора
.
Опр.
Полиномиальные операторы степени 1 наз.
линейными эволюционными операторами.
Они имеют след. вид:
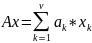 ,
,
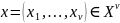
Примером
линейного эволюц. оператора кратности
(2,1) явл. оператор
суммирования
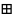 :
положим
:
положим
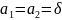 (
- ф-ция Дирака), тогда
(
- ф-ция Дирака), тогда
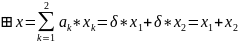
Оператор умножения
 явл. уже однородным эволюц. оператором
степени 2 кратности (2,1): положим
явл. уже однородным эволюц. оператором
степени 2 кратности (2,1): положим
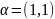 и
и
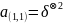 ,
тогда
,
тогда
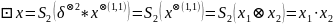
10.
Тензорное произведение эволюционных
операторов.
Рассмотрим
вначале тензорное произведение реакций
двух эволюц операторов:
Пусть А и В
– эволюц операторы кратностей
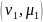 и
и
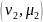 соотв-нно:
соотв-нно:
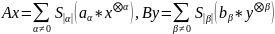 И
пусть
И
пусть
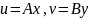 -реакций операторов А и В соотв-нно на
входные воздействия
-реакций операторов А и В соотв-нно на
входные воздействия
 .
Рассмотрим
тензорное произ-ние
.
Рассмотрим
тензорное произ-ние
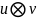 .
В силу билинейности и непрерывности
тензорного произведения имеем:
.
В силу билинейности и непрерывности
тензорного произведения имеем:
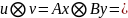 где
где
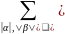 -оператор
сокращения переменных, действие которого
на произвольную ф-цию f,
имеющей
-оператор
сокращения переменных, действие которого
на произвольную ф-цию f,
имеющей
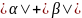 независимых переменных, определяется
формулой
независимых переменных, определяется
формулой
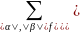
Лемма1:Пусть
a
и b-
финитные слева обобщённые вектор-функции
n
и m
переменных соответственно, w
и z-
финитные слева скалярные обобщённые
функции n
и m
переменных соответственно.Тогда
сараведливо следующее равенство: (a*w)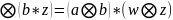 (2).
(2).
Применяя
равенство (2) к соотношению (1),получаем
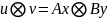 =
=
Полагая
же в равенстве (3) y=x,
имеем: =
=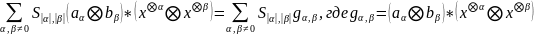 Теорема
(о тензорном произведении реакций двух
эволюционных операторов):
пусть А и В – эволюционные операторы:
Теорема
(о тензорном произведении реакций двух
эволюционных операторов):
пусть А и В – эволюционные операторы:
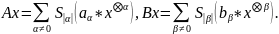 Тогда
справедлива формула:
Тогда
справедлива формула:
 (4)
(4)
_______________________________
Опр:
Композицией мультииндекса
 будем наз-ть такой конечный набор
мультииндексов
будем наз-ть такой конечный набор
мультииндексов
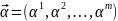 ,
где
,
где
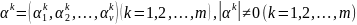 ,
таких, что для любого
,
таких, что для любого
 выполняется рав-во
выполняется рав-во
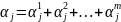 т.е.
т.е.
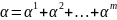 .
Мультииндексы
.
Мультииндексы
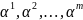 наз-ся частями
композиции
наз-ся частями
композиции
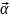 .
Множество
всех композиций мультииндекса
с m
частями будем обозначать
.
Множество
всех композиций мультииндекса
с m
частями будем обозначать
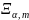 .
.
