§5. Основные задачи, связанные с прямой.

1. Угол между прямыми.

Рассмотрим две прямые l₁ и l₂ . Если эти прямые заданы своими общими уравнениями, то

косинус угла между ними может быть найден как косинус угла между их нормалями или направляющими векторами с помощью скалярного произведения: .

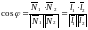Замечание. Направляющий вектор из нормального (и наоборот) легко получить следующим образом:

В случае задания прямых уравнениями с угловым коэффициентом, имеем соотношение:

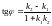
2. Условия параллельности и ортогональности двух прямых.

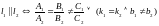
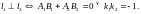
3. Расстояние от точки до прямой.

Вычислим расстояние от произвольной точки плоскости M^*(x^*, y^*) до прямой l: Ax+By+C = 0.

Пусть М(х,у) − произвольная точка прямой, − нормаль (рис.4).

Расстояние от т.M^* до прямой, очевидно, равно модулю проекции

•М^* вектора 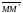на вектор нормали:

М

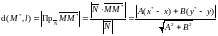
Т.к. точка 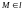, то Ах + Ву = − С и окончательно получаем:

Рис.4

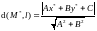
Замечание. Знак выражения Ах^*+Ву^*+С меняется при переходе точки через прямую.

§6. Алгебраические линии на плоскости.

Линии, описываемые алгебраическим уравнением n −го порядка от двух переменных, называют линиями или кривыми n −го порядка на плоскости.

Линии 1 – го порядка описываются уравнением Ах + Ву + С = 0 (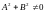 ) представляют собой прямые.

Уравнения 2 – го порядка : 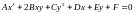,( 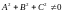) называют

кривыми 2 – го порядка и представляют собой целое семейство плоских кривых.

§7. Окружность.

Определение. Окружность − геометрическое место точек плоскости, равноудаленных от

заданной фиксированной точки плоскости, называемой центром окружности. Расстояние от

точек окружности до центра – радиус окружности.

Если центр окружности находится в т. М₀(х₀,у₀), а радиус равен r, то уравнение окружности может быть написано в следующем виде:

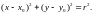
§8. Эллипс.

Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная.

Для вывода уравнения эллипса выберем фокусы в точках F₁(-c,0) и F₂(c,0) (c > 0) , а сумму расстояний обозначим через 2а (2a >2 c). Пусть М(х,у) – произвольная точка эллипса. Тогда:

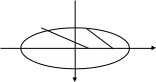y

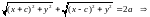
b М

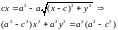
−a F₁ F₂ a x Обозначив a² − c² = b² , окончательно

−b получим:

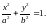
рис.5

Числа a и b называются полуосями эллипса (точки пересечения эллипса с осями координат имеют своими координатами числа а и b (рис.5)).

Отношение расстояния между фокусами эллипса к длине большой оси называется эксцентриситетом эллипса: 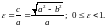Эксцентриситет характеризует форму

эллипса. При ε = 0 эллипс превращается в окружность, при ε = 1 − вырождается в отрезок.

Написанное выше уравнение называется каноническим уравнением эллипса. (Вообще, в геометрии словами каноническое уравнение, обычно, называют уравнение, содержащее в явном виде все основные геометрические характеристики объекта. См. например, каноническое уравнение прямой (§4))

Это уравнение является частным случаем уравнения 2 – го порядка (§6). Нетрудно видеть,

что любое уравнение 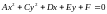представляет собой эллипс при условии

AC > 0. (Более общие условия будут выведены позже)

Пример. 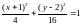− эллипс

с центром в т.(−1,2) и полуосями 2 и 4. 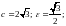F₁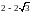(−1, ) и F₂(−1, ).

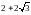Замечания. 1) Фокусы эллипса всегда расположены на больших полуосях .

2) Если правая часть = 0, то вырожденный эллипс (точка), если = −1 – мнимый эллипс.