- •Глава I. Векторная алгебра.
- •§1. Векторы в пространстве. Основные определения.
- •§2. Линейные операции над векторами.
- •I. Сложение векторов.
- •I I. Умножение вектора на число.
- •§3. Проекция вектора на ось.
- •§4. Линейно зависимые и линейно независимые системы векторов.
- •§5. Базис. Координаты. Размерность.
- •§6. Скалярное произведение.
- •§7. Скалярное произведение в координатной форме.
- •§8. Направляющие косинусы вектора.
- •§9. Ориентация базиса в пространстве.
- •§10. Векторное произведение.
- •§11. Смешанное произведение трех векторов.
- •Глава II. Аналитическая геометрия на плоскости и в пространстве.
- •§1. Декартова система координат.
- •§2. Простейшие задачи аналитической геометрии.
- •§2. Аналитическая геометрия на плоскости.
- •§3. Прямая на плоскости.
- •§4. Специальные виды уравнения прямой.
- •§5. Основные задачи, связанные с прямой.
- •§6. Алгебраические линии на плоскости.
- •§7. Окружность.
- •§8. Эллипс.
- •§9. Гипербола.
- •§10. Парабола.
- •§11. Кривые второго порядка – заключение.
- •§12. Аналитическая геометрия в пространстве.
- •§13. Плоскость в пространстве.
- •§14. Специальные случаи уравнения плоскости.
- •§15. Основные задачи, связанные с плоскостью.
- •§16. Прямая в пространстве.
- •§17. Основные задачи.
- •§18. Поверхности в пространстве.
- •§19. Поверхность вращения.
- •§20. Проекция линии пересечения двух поверхностей на координатную плоскость.
- •§21. Поверхности второго порядка. Исследование методом сечений.
- •§22. Эллипсоид.
- •§23. Гиперболоиды и конус.
- •§24. Параболоиды.
§12. Аналитическая геометрия в пространстве.
Поверхности в пространстве задаются
либо уравнением с тремя переменными:
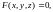
либо в
параметрической форме:
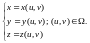
Линии в пространстве задаются пересечением двух поверхностей, или параметрически:
т.е.
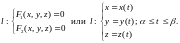
При решении задач в пространстве особенно важно знать геометрический смысл параметров, входящих в уравнения.
§13. Плоскость в пространстве.
Определение. Плоскостью называется геометрическое место концов векторов, имеющих общее начало и ортогональных данному ненулевому вектору, называемому нормальным вектором плоскости.
Для вывода
уравнения плоскости Р зафиксируем
т.
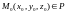 и нормальный вектор
и нормальный вектор
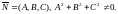 (рис.8).Тогда
(рис.8).Тогда
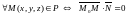 .
Отсюда получаем:
.
Отсюда получаем:
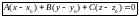 − уравнение плоскости, проходящей
через
− уравнение плоскости, проходящей
через
т.
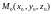 и ортогональной вектору
и ортогональной вектору
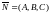 .
.
Если раскрыть
скобки и обозначить
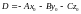 ,
то получим общее уравнение плоскости:
,
то получим общее уравнение плоскости:
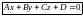
Замечание. И в общем уравнение плоскости коэффициенты А, В и С являются координатами
вектора нормали.
§14. Специальные случаи уравнения плоскости.
Уравнение плоскости, проходящей через три точки.
Пусть тт.
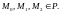 Необходимым и достаточным условием
принадлежности т. М той же плоскости
является компланарность векторов
Необходимым и достаточным условием
принадлежности т. М той же плоскости
является компланарность векторов
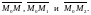 В свою очередь, условие компланарности
(гл.I,§11,св.2) приводит к
следующему уравнению:
В свою очередь, условие компланарности
(гл.I,§11,св.2) приводит к
следующему уравнению:
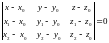
Уравнение плоскости в отрезках.
Возьмем в качестве предыдущих точек точки пересечения с осями координат:
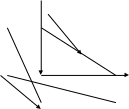 z
z
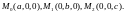
c Уравнение плоскости примет вид:
• М0
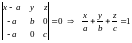
b y
a
х рис.8
§15. Основные задачи, связанные с плоскостью.
Условия параллельности, перпендикулярности, угол между плоскостями.
Даны две плоскости:

Все перечисленные условия следуют из геометрического смысла коэффициентов (§13).
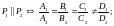


Расстояние от точки до плоскости.
Вычисляется так же, как в случае прямой
на плоскости (§5). Пусть
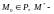 произвольная
точка пространства. Расстояние от точки
до плоскости равно модулю проекции
произвольная
точка пространства. Расстояние от точки
до плоскости равно модулю проекции
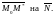
После
простых преобразований получим
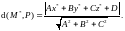
(#) III. Связка и пучок плоскостей.
Определение1. Множество плоскостей, проходящих через единственную общую точку М0 , называется связкой плоскостей с центром в т. М0 ( Обозначение − S(M0)).
Рассмотрим три плоскости, принадлежащие S(M0):
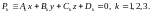 ……………………..(*)
……………………..(*)
Теорема. Уравнение
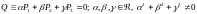 описывает связку плоскостей с центром
в данной точке.
описывает связку плоскостей с центром
в данной точке.
{Нужно доказать 2 утверждения: 1)
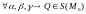 2)
2)
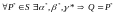 .
.
Так как все слагаемые Q равны нулю в т. М0 , то и Q = 0 в этой точке.
Так как СЛАУ (*) имеет единственное решение (x0,y0,z0), то из правила Крамера следует,
что определитель системы отличен от
нуля, т.е. векторы
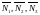 линейно независимы и
линейно независимы и
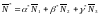 .
Значение D = D*
, т.к. все плоскости проходят через т. М0
}
.
Значение D = D*
, т.к. все плоскости проходят через т. М0
}
Определение2. . Множество плоскостей, проходящих через общую прямую – ось плоскостей,
называется пучком плоскостей.
Теорема. Уравнение пучка плоскостей имеет вид:
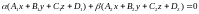 ,
при условии
,
при условии