Раздел 1. Теория пределов

§1.1. Предел и непрерывность функции

1. Предел функции в точке

2. Непрерывность функции в точке

3. Точки разрыва

4. Вычисление пределов

Предел функции — одно из основных понятий современной математики. С его помощью вводятся многие другие важные математические понятия.

ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ

Под пределом переменной понимают такую постоянную, к которой неограниченно приближается эта переменная: начиная с некоторого момента ее значения отличаются от данной постоянной на величину, модуль которой меньше лю­бого положительного числа, каким бы малым оно ни было. Другими словами, в изменении переменной величины можно указать такой момент, начиная с которого модуль раз­ности переменной и постоянной становится и остается меньше любого, сколь угодно малого положительного числа.

Введем понятие предела функции y=f(x), определенной в некотором интервале, содержащем точку х=а (в самой точке х=а заданная функция может быть и не определена).

Число b называют пределом функции y=f(x) при х, стремящемся к а (или в точке а), если для любого числа ε > 0 существует такое число δ > 0, что при всех х, удовлетворяющих условию 0 < |х - а| < δ, (1)

выполняется неравенство | f (x) – b | < ε. (2)

Употребляются следующие обозначения для предела функции при х, стремящемся к а:

Отметим, что х стремится к а произвольным образом: аргумент х может принимать значения или меньше а, или больше а, или те и другие (х<а и х>а). Выясним геометрический смысл понятия предела функции y = f(x) в точке х=а, воспользовавшись ее графиком (рис. 1).

Н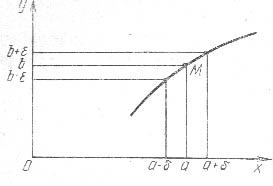 еравенство (1) означает, что точка х отстоит от точки а на расстоянии, меньшем δ, т. е. принадлежит интервалу (а - δ; а + δ) или δ-окрестности точки а на оси Ох. Эту окрестность обозначают через О (а, δ). Из неравенства (2) видно, что значения функции y=f(x) при указанных значениях аргумента х попадают в интервал (b - ε; b + ε) оси Оу, т. е. принадлежат ε-окрестности точки b на этой оси. Эту окрестность обозначим 0(b, ε). Следовательно, если , то точка М графика этой функции будет находиться в полоске шириной 2ε, ограниченной прямыми у = b - ε, у = b + ε для всех значений х, отстоящих от точки а меньше, чем на δ. Другими словами, если когда х попадает в δ-окрестность точки a, f(x) находится в ε-окрестности точки b.

Таким образом, выражение «функция f(x) в точке х=а имеет предел b» означает следующее: если значения аргу­мента достаточно мало отличаются от числа а, то соответ­ствующие значения функции f(x) достаточно мало отлича­ются от числа b. Иначе говоря, если значения аргумента неограниченно приближаются к постоянной а, то соответствующие значения функции неограниченно приближаются к постоянной b.

Из определения предела функции следует, что предел постоянной равен этой постоянной: (3)

Рассматривают также односторонние пределы функции f(x) в точке х=а: предел слева (когда х стремится к а, оставаясь меньше а) и предел справа (когда х стремится к а, оставаясь больше а). Для этих пределов вводят обозначения:

и

Запись x→a - 0 означает, что х стремится к а, оставаясь меньше а, а запись х→а + 0 — что х стремится к а, оставаясь больше а. Когда а = 0, вместо 0—0 пишут —0, вместо 0 + 0 пишут +0, поэтому обозначения односторонних пределов принимают вид: и

Сформулируем определения односторонних пределов функции f(x).

Число b ₁ называют пределом слева функции f(x) в точке а, если для любого числа ε >0 существует такое δ>0, что |f(x)-b₁ | < ε (4)

при всех х, удовлетворяющих условию а — δ < х < а. (5)

Этот односторонний предел обозначают так

Число b₂ называют пределом справа функции f(x) в точке а, если для любого числа ε > 0 существует такое δ > 0, что | f(x) – b₂ | < ε (6)

при всех х, удовлетворяющих условию а < х < а + δ.

Этот односторонний предел обозначают так (7)

Очевидно, если односторонние пределы равны, т. е. b₁ = b₂ (см. рис. 2А), предел функции f(x) в точке х = а существует и равен этим односторонним пределам. В самом деле, если b₁ = b₂= b и выполняются неравенства (4) — (7), то будет выполняться и неравенство (2) при условии (1):

Е сли односторонние пределы различны (рис. 2Б) или хотя бы один из них не существует, то не существует и предел функции в точке х = а.

Рис. 2А Рис. 2Б

НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ

Непрерывность функции является важным математическим понятием. Функцию считают непрерывной, если при постепенном (непрерывном) изменении аргумента значения ее меняются также постепенно, без скачков. Наглядному представлению о непрерывности функции способствует ее график, который можно построить, не отрывая карандаш от бумаги. Если функция имеет разрыв, то начертить таким образом ее график не представляется возможным.

Функцию y=f(x), определенную на интервале (a; b), называют непрерывной в точке х₀ из (a; b), если предел этой функции в точке х₀ равен ее значению при х = х₀ :

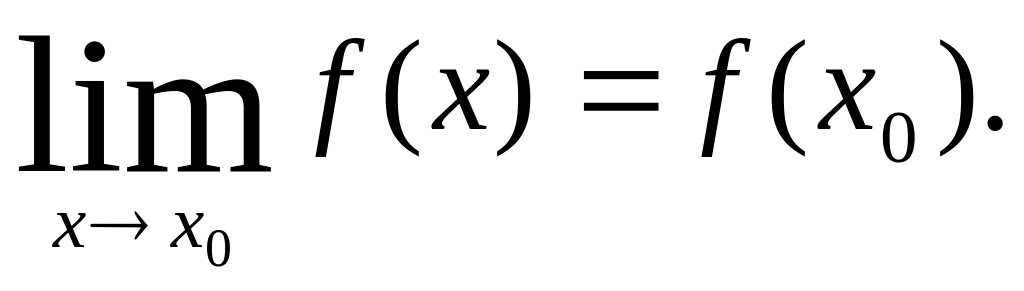(1)

ТОЧКИ РАЗРЫВА ФУНКЦИИ

Рассмотрим функцию y=f(x), определенную на интервале (a; b), кроме, может быть, точки Значение аргумента х₀ называют точкой разрыва данной функции, если в ней функция определена, но не является непрерывной или не определена в этой точке. Говорят, что функция имеет разрыв при х = х₀ .

Среди точек разрыва функции различают - точки устранимого разрыва, - точки разрыва первого рода, - точки разрыва второго рода.

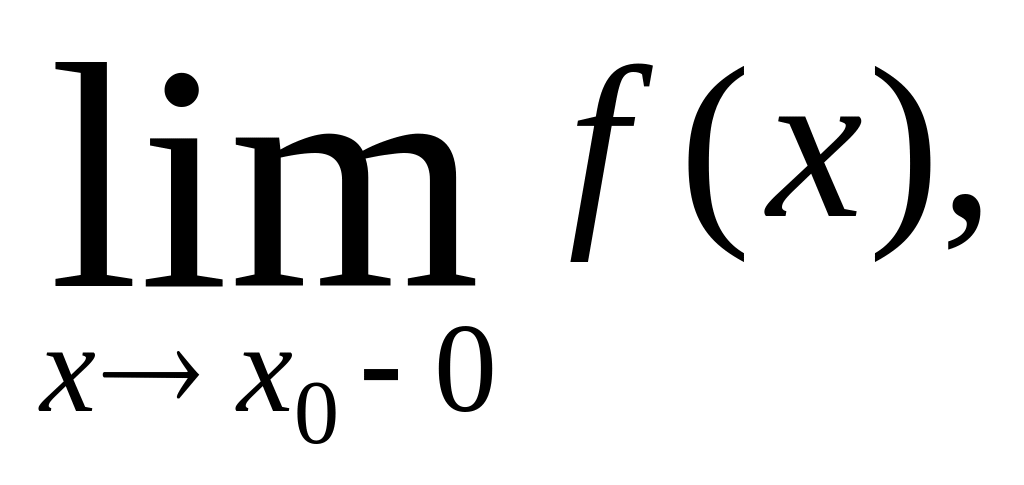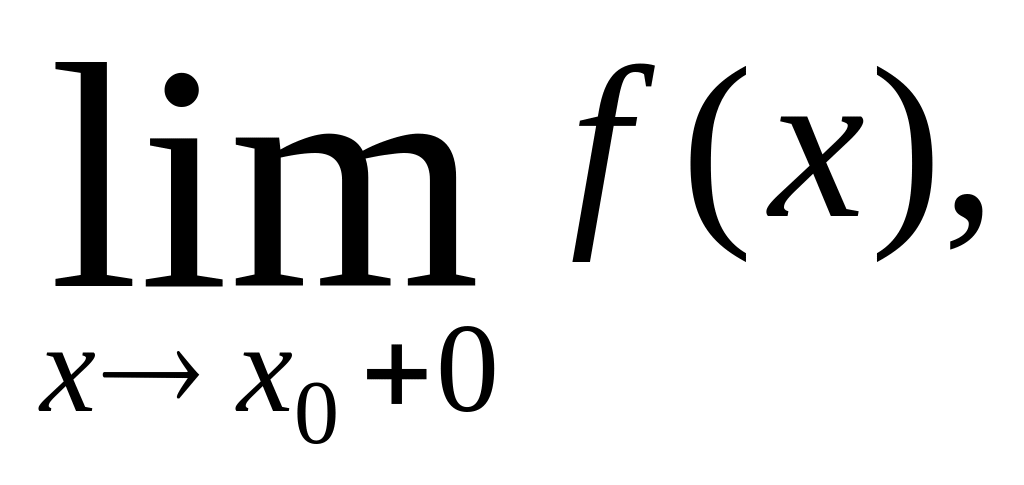• Если функция y=f(x) разрывна в точке х₀ и имеет в ней конечные равные односторонние пределы f (x₀ – 0) = f (x₀ +0) = то х₀ называют точкой устранимого разрыва.

• Если х₀ – точка разрыва функции y=f(x) и существуют конечные односторонние пределы f (x₀ – 0) и f (x₀ +0), причем f (x₀ – 0) ≠ f (x₀ +0), то х₀ называют точкой разрыва первого рода. Разность f (x₀ +0) - f (x₀ – 0) называют скачком функции f(x) в точке х₀.

• Если х₀ – точка разрыва функции y=f(x) и хотя бы один из односторонних пределов либо является бесконечным, либо не существует, то х₀ называют точкой разрыва второго рода.

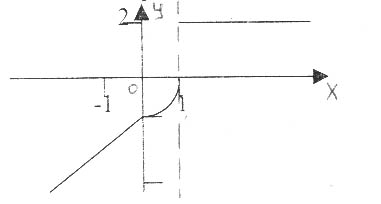
Пример 1. Функция задается различными аналитическими выражениями для различных областей изменения независимой переменной. Требуется: Найти точки разрыва функции, если они существуют; Найти скачок функции в каждой точке разрыва; Сделать чертеж. у1 = х – 1 непрерывна для всех х < 0; у2 = х2 – 1 непрерывна в каждой точке из [0; 1]; у3 = 2 непрерывна в каждой точке интервала (1; ∞). Точки, в которых функция может иметь разрыв, это точки х1 = 0 и х2 = 1, где функция меняет свое аналитическое выражение. Исследуем точку х1 = 0: y (0) = - 1, т.е. точка х1 = 0 есть точка непрерывности функции. Исследуем точку х2 = 1: y (1) = 0, т.е. точка х2 =1 – точка разрыва первого рода. Скачок функции: 1 – 0 = 1. Сделаем чертеж:

Проверочная работа № 1

Функция задается различными аналитическими выражениями для различных областей изменения независимой переменной. Требуется:

1. Найти точки разрыва функции, если они существуют;

2. Найти скачок функции в каждой точке разрыва;

3. Сделать чертеж.

Вариант 1. y = 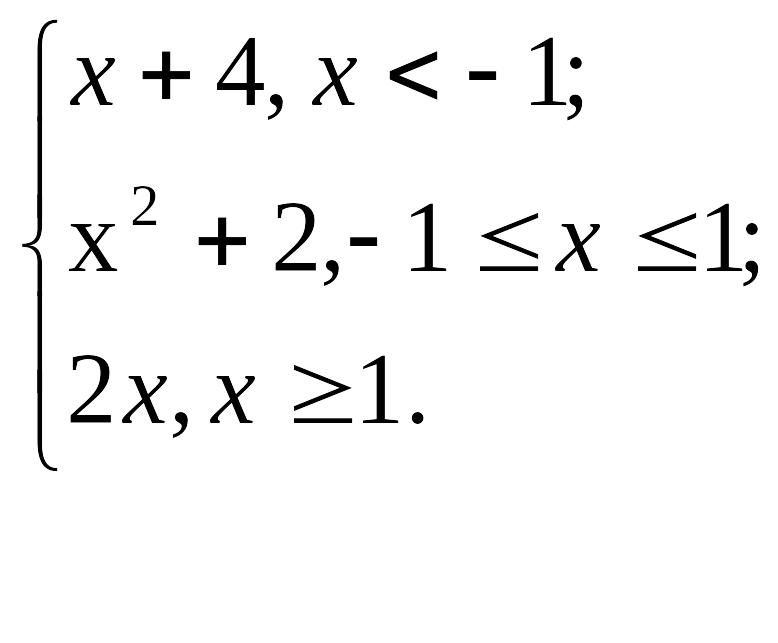Вариант 2. y =

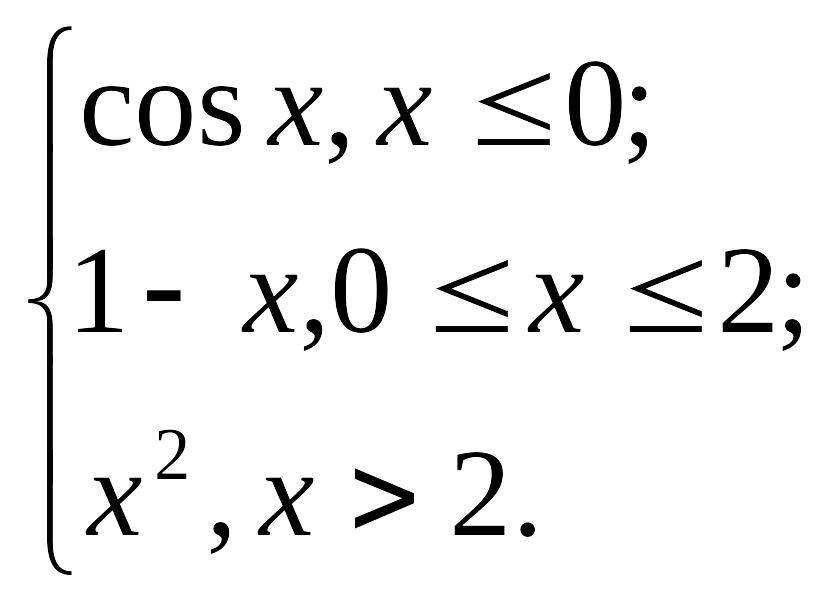
Вариант 3. y = 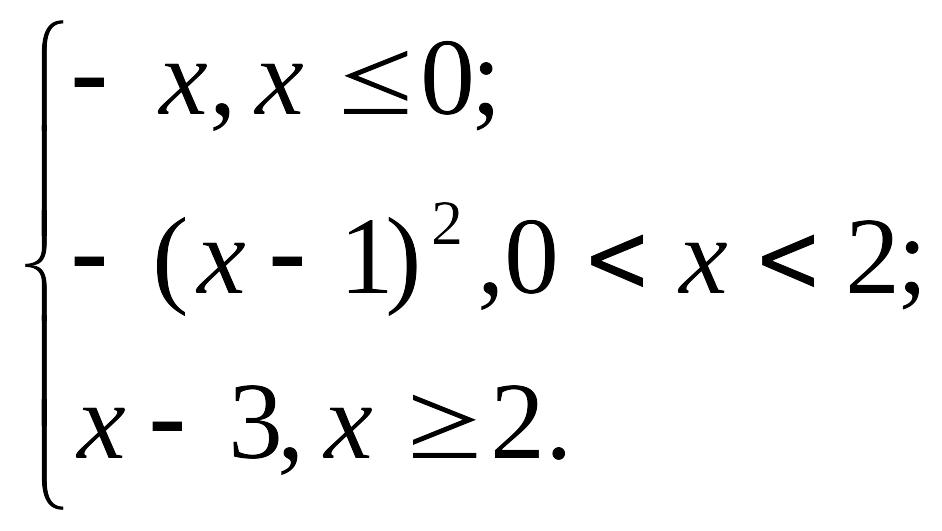Вариант 4. y =

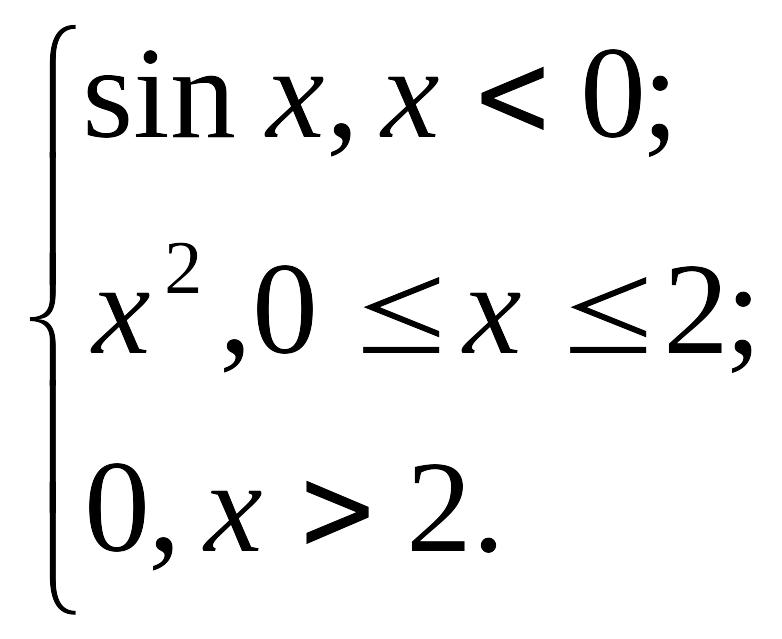
Вариант 5. y = 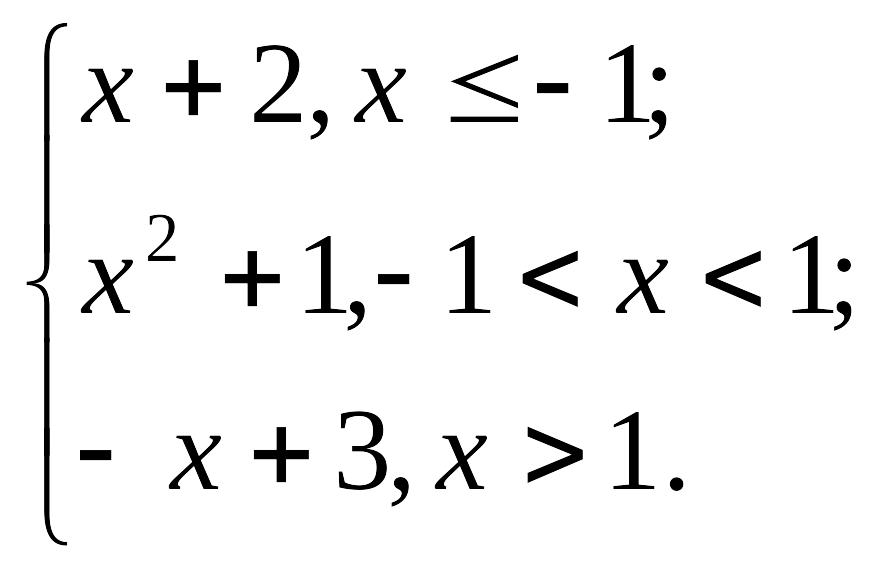Вариант 6. y =

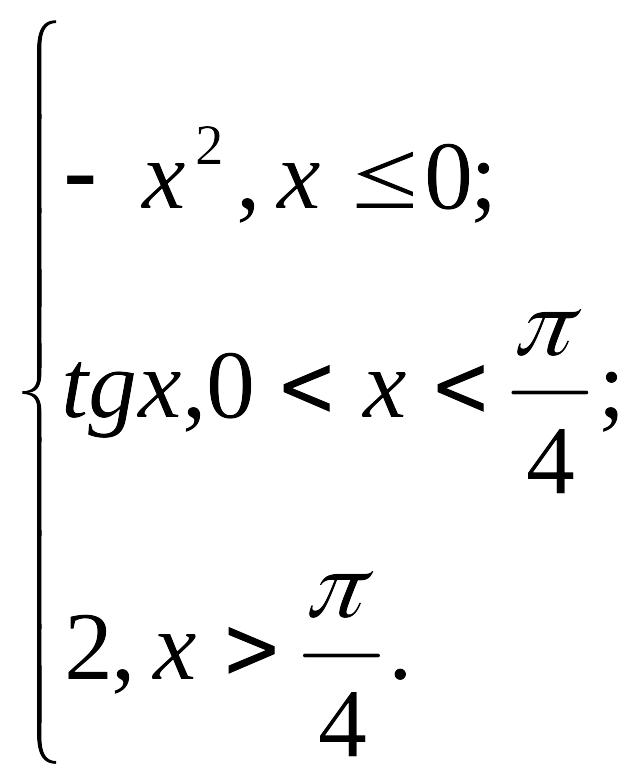
Вариант 7. y = 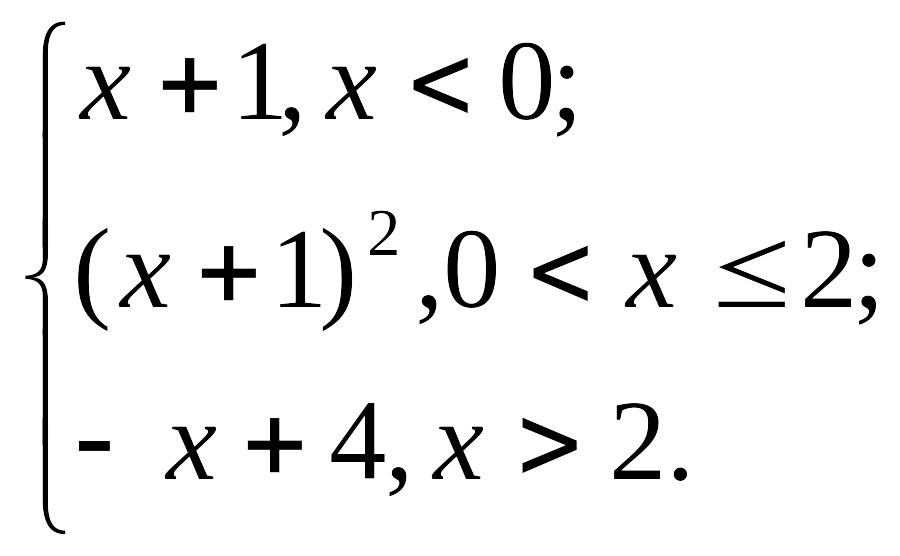Вариант 8. y =

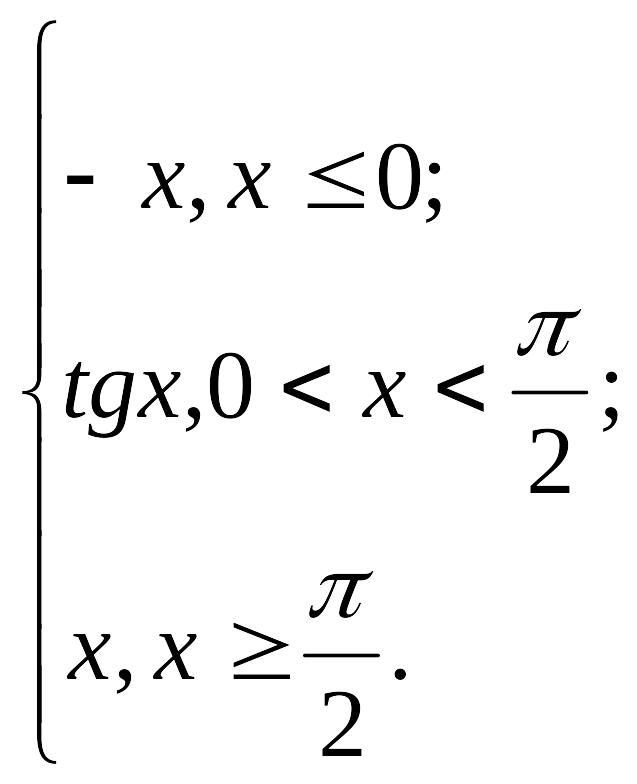
Вариант 9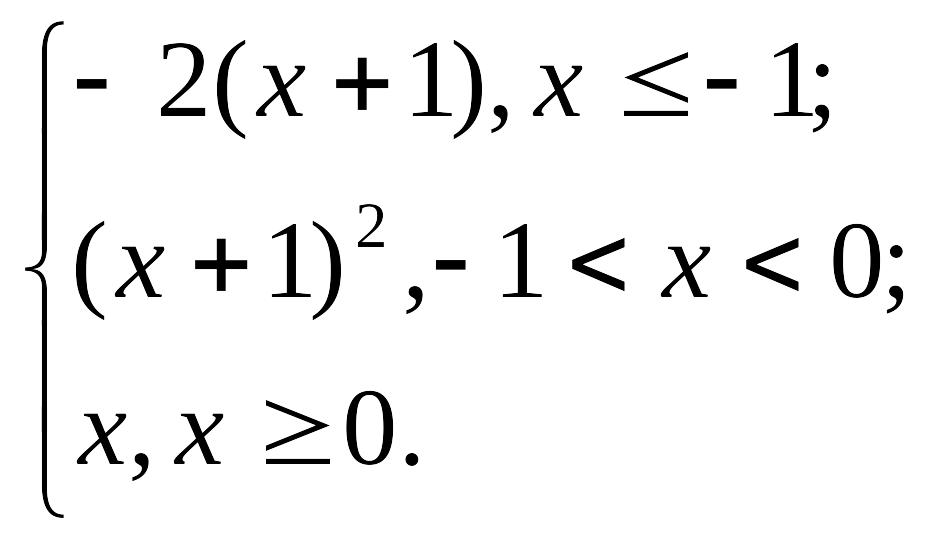. y = Вариант 10. y =