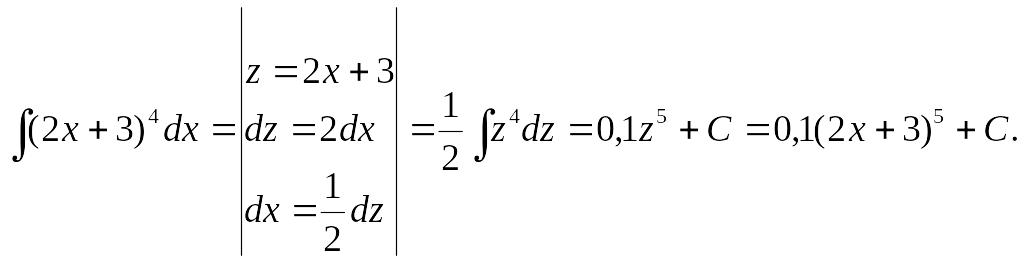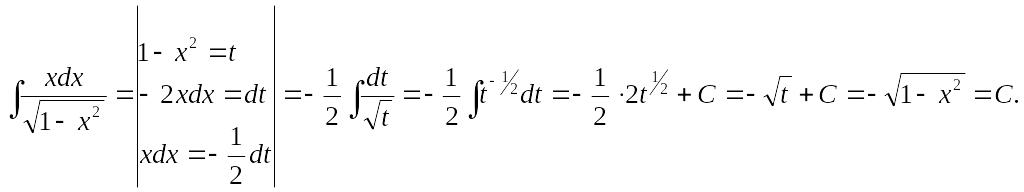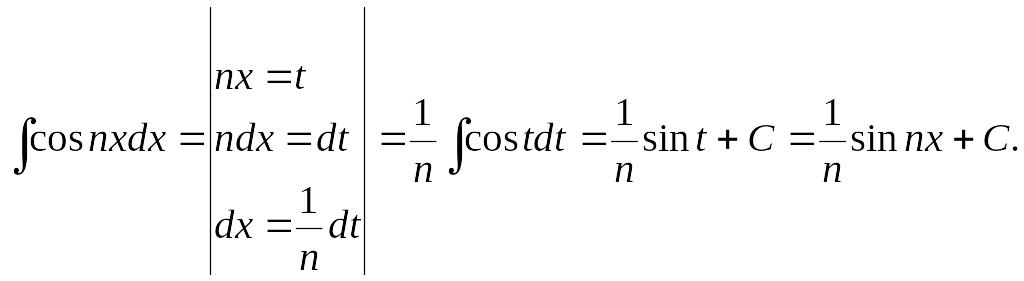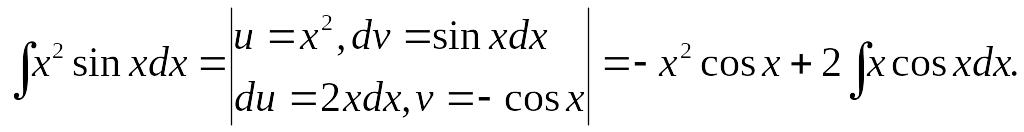§ 3.3. Основные табличные интегралы

Основные формулы интегрирования

Из определения интеграла следует, что для того чтобы проинтегрировать функцию, нужно найти ее первообразную. Для ряда функций это легко сделать, используя соответствующую формулу дифференцирования.

Например, мы знаем, что (arcsinx)' = 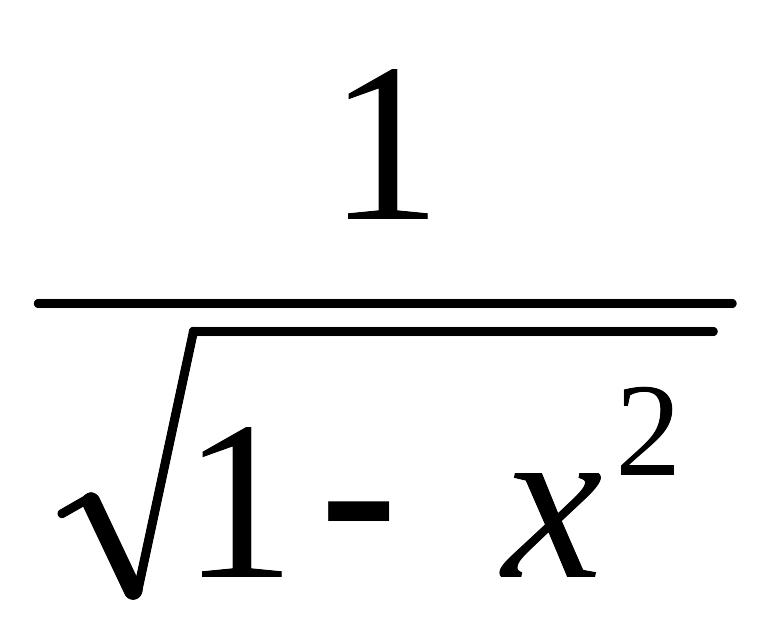; отсюда следует, что = arcsinx +С.

Итак, формулы интегрирования получаются обращением соответствующих формул дифференцирования. Выпишем в таблицу основные интегралы.

I. , при n ≠ -1. II. ; III. ;

IV. ; V. ; VI. ; VII. ; VIII. ;

IX. ; X. .

Интегралы, приведенные в этой таблице, называются табличными интегралами.

Для вывода этих формул, как уже отмечалось, используется свойство 5 неопределенного интеграла, а именно дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал — подынтегральное выражение.

Формула I справедлива при любом п, кроме п= — 1, так как в этом случае знаменатель обращается в нуль и выражение теряет смысл.

Вычисление интегралов способом приведения их к табличным с помощью преобразования подынтегрального выражения и применения свойств 2 и 3 неопределенного интеграла называется непосредственным интегрированием. При этом полезно запомнить, что (формула I при n=0).

Найти интеграл и сделать проверку. Решение. Согласно свойству 2 постоянный множитель 3 вынесем за знак интеграла; получим . Проверка. . Так как получено подынтегральное выражение, то интеграл найден правильно.

§ 3.4. Основные методы интегрирования:

ПОДСТАНОВКОЙ И ПО ЧАСТЯМ

1. Способ подстановки (замены переменной)

2. Способ интегрирования по частям

1. Способ подстановки (замены переменной)

Если заданный интеграл с помощью алгебраических преобразований трудно или невозможно свести к одному или нескольким табличным интегралам, то для его отыскания применяют особые способы, одним из которых является способ подстановки (замены переменной).

Заметим, что все способы интегрирования имеют целью свести данный интеграл к табличному с помощью тех или иных искусственных приемов.

Способ подстановки заключается в следующем: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множителя, на который всегда можно умножить и разделить подынтегральное выражение).

Например, в интеграле ∫sinxcosxdx удобно произвести замену t=sinx, так как оставшаяся часть подынтегрального выражения равна cosxdx = dt. Тогда перепишем данный интеграл в виде

∫sinx cosxdx = ∫ t dt.

Полученный интеграл является табличным; он находится по формуле I:

∫tdt=1/2 t² + C.

Далее, произведя обратную замену t = sinx, получим ответ:

½ t² + C=1/2 sin²x + C.

Решение этого примера можно кратко оформить так:

Напомним, что если при интегрировании одной и той же функции разными способами получили различные результаты, то необходимо показать, что они отличаются на постоянную величину.

Так, рассмотренный выше пример можно решить иначе, если применить формулу sin2х=2sinхcosх. Тогда получим

Результат по виду отличается от найденного ранее; однако, преобразуя первый результат, имеем

Отсюда видно, что разность функций равна 1/4, т. е. постоянному числу.

Естественно возникает вопрос: как правильно выбрать подстановку? Это достигается практикой в интегрировании. Все же можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования.

Правило интегрирования способом подстановки состоит в следующем:

1°. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).

2°. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.

3°. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.

4°. Производят замену под интегралом.

5°. Находят полученный интеграл.

6°. В результате производят обратную замену, т. е. переходят к старой переменной. Результат полезно проверить дифференцированием.

Найти неопределенные интегралы способом подстановки. 1) . Решение. Проверка. d(0,1(2x +3)5 +C) = 0,5 (2x + 3)4 (2x)'dx = (2x +3)4dx. 2) Решение. 3) Решение.

2. Способ интегрирования по частям

При интегрировании функций, содержащих произведения, логарифмы и обратные тригонометрические функции, бывает удобно воспользоваться способом интегрирования по частям.

Выведем формулу интегрирования по частям.

Интегрируя обе части равенства d(uv) = udv + v du, получим

∫d(uv)= ∫udv +∫vdu или uv= ∫udv+ ∫vdu,

откуда ∫udv = uv - ∫vdu. (1)

С помощью формулы (5) нахождение интеграла ∫udv сводится к нахождению интеграла ∫vdu, который может оказаться или проще данного, или даже известным.

При практическом использовании формулы интегрирования по частям данное подынтегральное выражение представляют в виде произведения двух сомножителей, которые обозначают u и dv. Множитель u стараются выбрать так, чтобы и' было проще, чем и.

1) Решение. Интеграл содержит произведение двух функций х и cosx. Способ подстановки не дает возможности найти этот интеграл. Обозначим х = и, cosxdx = dv; тогда dx = du; v = sinx. Применим формулу интегрирования по частям: Приняв х= и, мы получили и'= 1 и интеграл ∫vdu оказался проще, чем ∫udv. Если же в этом интеграле сделать другую замену: соsх=и, xdx=dv, то легко убедиться, что полученный интеграл окажется сложнее исходного, т. е. замена окажется неудачной. Умение определить целесообразность той или иной замены приходит с приобретением навыка. Иногда формулу интегрирования по частям приходится применять дважды. 2) Решение. Для нахождения полученного в правой части равенства интеграла снова интегрируем по частям: (см. решение примера 1) выше). В результате получаем окончательный ответ: