- •Кафедра общепрофессиональных дисциплин
- •Домашняя подготовка
- •Лабораторное занятие
- •Составление и защита отчета
- •Лабораторная работа №1 дискретизация и восстановление непрерывных сигналов
- •1 Цель работы
- •2 Теоретические основы дискретизации сигналов
- •3 Описание лабораторной установки
- •4 Домашняя подготовка к лабораторной работе
- •5 Экспериментальная часть
- •6 Содержание отчёта
- •7 Контрольные вопросы
- •Лабораторная работа №2 амплитудная модуляция
- •1 Цель работы
- •2 Элементы теории модуляции
- •Амплитудно-модулированный сигнал записывается в виде
- •В цепь затвора транзистора vт поступает сумма трёх напряжений
- •Как видно из (4), статическая модуляционная характеристика выражается формулой:
- •3 Характеристика лабораторной установки
- •4 Домашняя подготовка к лабораторной работе
- •5 Порядок выполнения лабораторной работы
- •6 Содержание отчёта
- •7 Контрольные вопросы
- •Лабораторная работа №3 детектирование амплитудно-модулированных сигналов
- •1 Цель работы
- •2 Элементы теории детектирования
- •3 Характеристика лабораторной установки
- •4 Домашняя подготовка к лабораторной работе
- •5 Порядок выполнения лабораторной работы
- •6 Содержание отчёта
- •7 Контрольные вопросы
- •Лабораторная работа №4 исследование функций автокорреляции случайных процессов
- •Цели работы
- •Некоторые сведения из теории случайных
- •Характеристика лабораторной установки
- •Подготовка к лабораторной работе
- •5 Лабораторное задание
- •Требования к отчёту
- •Контрольные вопросы
- •Лабораторная работа № 5 исследование функций взаимной корреляции случайных процессов и их производных
- •Цели работы
- •2 Некоторые сведения из теории случайных процессов
- •Функция взаимной корреляции процесса x3(t) и его производной по времени может быть представлена в виде:
- •3 Характеристика лабораторной установки
- •Подготовка к лабораторной работе
- •Лабораторное задание
- •Требования к отчету
- •Контрольные вопросы
- •Лабораторная работа № 6 исследование автокорреляционной функции суммы периодического сигнала и широкополосного шума
- •Цель работы
- •2 Автокорреляционная функция суммы сигнала
- •В этом случае смесь y(t) является нестационарным случайным процессом. Функцией корреляции смеси сигнала и шума y(t) в теории случайных процессов [3] принять считать:
- •3 Характеристика лабораторной установки
- •4 Подготовка к лабораторной работе
- •5 Лабораторное задание
- •6 Требования к отчету
- •7 Контрольные вопросы
- •Лабораторная работа № 7 оптимальная фильтрация сигналов известной формы
- •1 Цель работы
- •2 Основы теории оптимальной фильтрации детерменированных сигналов в присутствии флуктуационных помех
- •Удельная мощность помехи на выходе фильтра может быть найдена из выражения
- •3 Характеристика лабораторной установки
- •4 Подготовка к лабораторной работе
- •Лабораторное задание
- •6 Требования к отчету
- •7 Контрольные вопросы
- •Лабораторная работа № 8 исследование lc-автогенератора
- •1 Цель работы
- •Генерация гармонических колебаний
- •Характеристика лабораторной установки
- •Подготовка к выполнению работы
- •Лабораторное задание
- •6 Содержание отчета
- •7 Контрольные вопросы
Контрольные вопросы
7.1 Дать определения функции корреляции, функции ковариации, коэффициента корреляции. Указать различия между приведёнными понятиями.
7.2 Записать выражения для функции корреляции с усреднением по множеству значений и с усреднением по времени. Указать, при каких условиях результаты усреднения по множеству значений и по времени одинаковы.
|
|
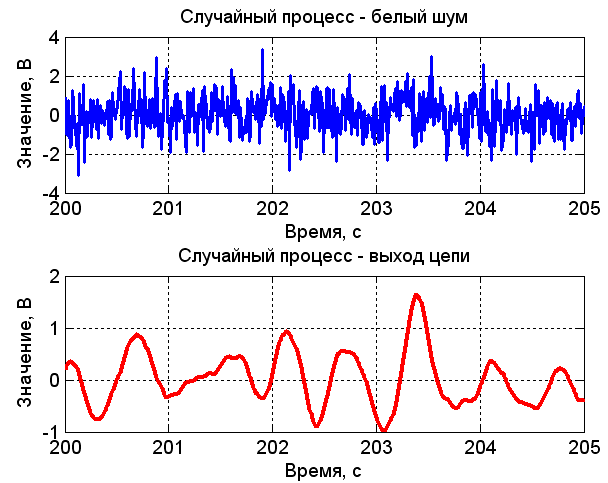
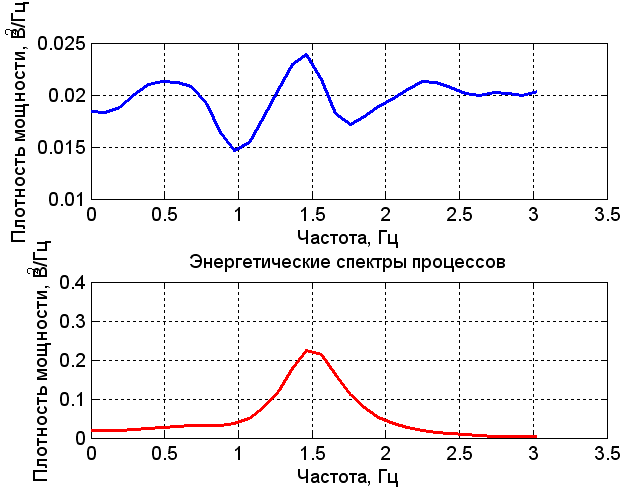
Рисунок 4 – Временные и спектральные диаграммы
при моделировании RLC-цепи
7.3 Какой может быть функциональная схема коррелометра при использовании метода усреднения по множеству реализаций?
7.4 Разработать функциональную схему коррелометра с использованием усреднения по времени, построенного на базе ЭЦВМ.
7.5 На вход линейной цепи поступает стационарный случайный процесс с известной функцией корреляции. Указать метод расчёта функции корреляции выходного процесса в стационарном режиме при известном комплексном коэффициенте передачи цепи.
7.6 Дать определение стационарного случайного процесса в узком и широком смысле.
7.7 Что такое эргодическое свойство стационарного случайного процесса? Привести пример стационарного процесса не обладающего эргодическим свойством.
7.8 Дать определение спектральной плотности мощности стационарного случайного процесса. Какими свойствами обладает спектральная плотность мощности?
7.9 Разработать функциональную схему аппаратурного метода исследования спектральной плотности мощности (анализатора спектральной плотности мощности).
7.10 Указать связь спектральной плотности мощности с функцией корреляции случайного процесса.
7.11 Перечислить основные свойства автокорреляционной функции стационарного случайного процесса, обладающего эргодическим свойством.
7.12 Дать определение времени корреляции стационарного случайного процесса. Разработать функциональную схему экспериментального измерения времени корреляции случайного процесса.
Лабораторная работа № 5 исследование функций взаимной корреляции случайных процессов и их производных
Цели работы
Исследование функций взаимной корреляции стационарных случайных процессов и их производных, изучение методов аппаратурного корреляционного анализа совокупности случайных процессов.
2 Некоторые сведения из теории случайных процессов
Функцией взаимной корреляции случайных процессов X(t) и Y(t) называется смешанный центральный момент второго порядка системы двух сечений Х(t1), Y(t2), рассматриваемый как функция моментов времени t1 и t2:
![]() (1)
(1)
где W(x1,y2) – плотность вероятности системы случайных величин X1 и Y2;
x1, y2 – значения сечений X(t1) и Y(t2) соответственно;
mx1, my2 – математические ожидания сечений X(t1) и Y(t2).
В случае стационарных и стационарно связанных случайных процессов X(t) и Y(t) функция взаимной корреляции не зависит от значений моментов времени t1 и t2, а зависит от их разности τ = t1 - t2.
Функция взаимной корреляции Кху(τ) характеризует линейную статистическую связь стационарных и стационарно связанных случайных процессов X(t) и Y(t) в зависимости от их временного сдвига относительно друг друга. В точках, где значения функции взаимной корреляции Кху(τ) равны нулю линейная зависимость Y(t) от X(t) и наоборот отсутствует.
Рассмотрим
основные свойства функции взаимной
корреляции
![]() .
Здесь угловые скобки означают вычисление
математического ожидания. Предполагается
также, что процессы X(t)
и Y(t)
имеют нулевые математические ожидания.
При выборе индексов обозначения функции
Кху(τ)
на первое
место условно ставится опережающий
процесс. Отсюда следует:
.
Здесь угловые скобки означают вычисление
математического ожидания. Предполагается
также, что процессы X(t)
и Y(t)
имеют нулевые математические ожидания.
При выборе индексов обозначения функции
Кху(τ)
на первое
место условно ставится опережающий
процесс. Отсюда следует:
![]() (2)
(2)
Таким образом перемена порядка следования индексов эквивалентна изменению знака переменной τ.
В общем случае функция корреляции Кху(τ) не является ни четной, ни нечетной функцией. Поэтому взаимная спектральная плотность мощности процессов X(t) и Y(t) в общем случае является комплексной функцией.
![]() (3)
(3)
Рассмотрим ряд конкретных функций взаимной корреляции.
В качестве первого примера найдем функцию взаимной корреляции между процессами на выходе и на входе линейной цепи. Выражение, связывающее выходной и входной процессы в указанном выше случае имеет вид:
![]() (4)
(4)
где g(t) – импульсная реакция цепи.
 (5)
(5)
Полученное выражение справедливо как для переходного, так и для стационарного режима. В стационарном режиме пределы интегрирования могут быть бесконечными, а функция корреляции не зависит от времени. Тогда:
![]() (6)
(6)
где Кх(τ) – функция автокорреляции входного процесса Х(t).
Таким образом, функция взаимной корреляции стационарных процессов на выходе и входе линейной цепи равна свертке функции корреляции входного процесса и импульсной реакции цепи.
Применяя к левой и правой части (6) преобразование Фурье в форме, представленной равенством (3), можно получить:
![]() (7)
(7)
где Syx(jω) – взаимная спектральная плотность мощности процессов Y(t) и X(t);
K(jω) – коэффициент передачи цепи;
Sx(ω) – спектральная плотность мощности процесса X(t).
Взаимная спектральная плотность мощности входного X(t) и выходного Y(t) процесса может быть получена обращением по Фурье взаимной функции корреляции Kxy(τ), которая связана с Kyx(τ) равенством (2).
 (8)
(8)
где проведена замена переменной интегрирования τ на –θ.
Используя полученное выражение и равенство (7), можно получить выражение для взаимной спектральной плотности процессов на входе и выходе линейной цепи:
![]() (9)
(9)
Полученные результаты можно использовать для исследования функции взаимной корреляции случайного процесса и его производной по времени.
Как известно из теории цепей, коэффициент передачи дифференцирующей цепи, процесс на выходе которой равен производной входного процесса, можно представить выражением:
![]() (10)
(10)
В
этом случае функция взаимной корреляции
производной случайного процесса
![]() и исходного процесса X(t)
может быть записана в виде:
и исходного процесса X(t)
может быть записана в виде:
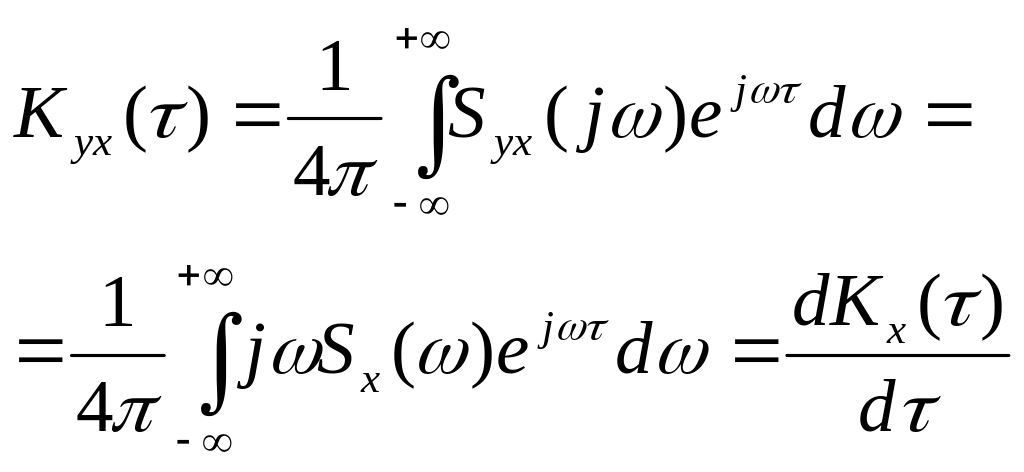 (11)
(11)
Таким образом, функция взаимной корреляции между производной и случайным процессом равна производной функции корреляции случайного процесса.
Отметим
основные свойства функции взаимной
корреляции
![]() ,
где
,
где
![]() – производная процесса X(t).
– производная процесса X(t).
Известно, что функция корреляции Kx(τ) стационарного случайного процесса является чётной функцией τ и в точке τ=0 имеет максимум, равный дисперсии. Следовательно, функция взаимной корреляции является нечетной функцией и
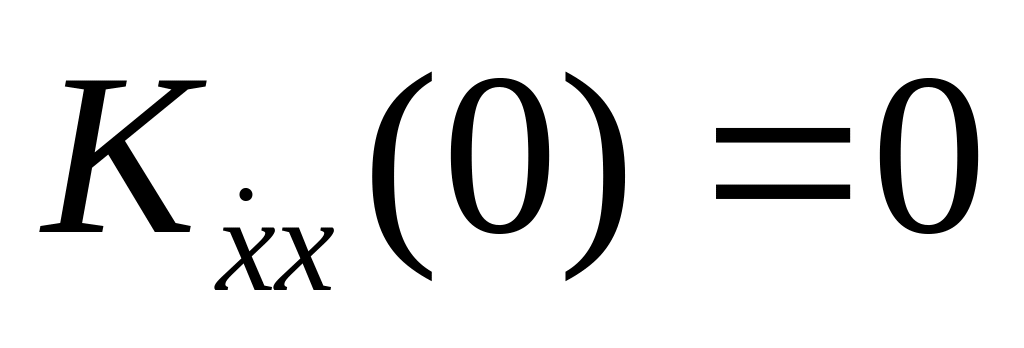 ,
то есть в одинаковые моменты времени
стационарный процесс и его производная
не коррелированны, а в случае нормального
распределения X(t)
и независимы.
,
то есть в одинаковые моменты времени
стационарный процесс и его производная
не коррелированны, а в случае нормального
распределения X(t)
и независимы.Если функция корреляции Kx(τ) недифференцируема, то случайный процесс X(t) считается недифференцируемым.
В связи с тем, что функция Kx(τ) в начале координат максимальна, то ее производная при τ = 0 равна нулю. Поэтому при монотонном характере функции корреляции Kx(τ) при τ > 0 ее производная отрицательна, а при τ < 0 положительна. В силу того, что функция корреляции Kx(τ) является четной, то функция не четна. При увеличении абсолютного значения τ функция взаимной корреляции стремится к нулю.
Рассмотрим функции взаимной корреляции случайных процессов на выходах цепей б) и в) лабораторной работы № 4 (см. рисунок 2 работы № 4) и их производных. Принципиальные схемы цепей б) и в) представлены на рисунке 1.

Рисунок 1 – Принципиальные схемы цепей, формирующих
случайные процессы X2(t) и X3(t)
Резистор R в цепи в) может быть замкнут специальным проводником.
Нормированные корреляции процессов X1(t) и X3(t) имеют вид:
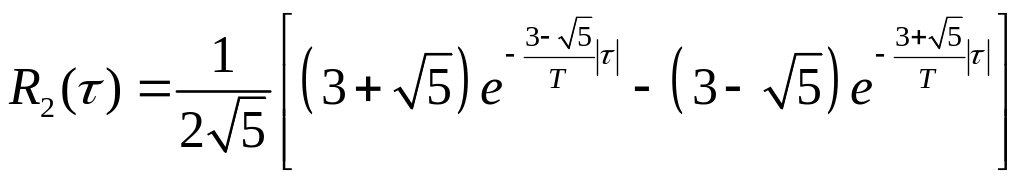 (12)
(12)
где T=RC;
![]() (13)
(13)
где
![]() ,
,
![]() ,
,
![]() ,
,
r – сопротивление потерь в катушке индуктивности цепи в).
Равенство (13) получено в предположении, что резистор R замкнут (на схеме рисунка 1,в отсутствует).
Аналогично,
функция взаимной корреляции случайного
процесса X2(t)
и его производной по времени
![]() равна:
равна:
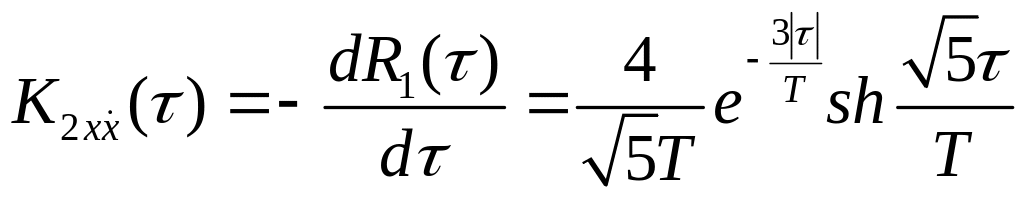 (14)
(14)
где
![]() – функция гиперболического синуса.
– функция гиперболического синуса.