5.3. Количественное определение измерительной

ИНФОРМАЦИИ

Информацию, получаемую от объектов контроля (исследо­вания), передаваемую по каналам связи, обрабатываемую и воспроиз­водимую приборами, можно определять количественно. Количественная характеристика информации не зависит от ее физического содержания, от физической природы сигналов, ее передающих, и от способов реали­зации приборов. В результате приема получателем сообщения о конт­ролируемом или изучаемом объекте, явлении, событии у него уменьша­ется степень неопределенности сведений о них или степень неопреде­ленности сложившегося у него образа изучаемого объекта. Имеются статистические характеристики этой степени неопределенности. Коли­чеством информации, содержащимся в сообщении, считается разность значений двух степеней неопределенности: 1) до получения сообще­ния; 2) после получения сообщения.

При измерениях происходит отбор, передача, обработка и воспро­изведение информации непрерывного характера, т. е. количественных значений различных непрерывных физических величин. Но чтобы по­нять, каким образом оценивается количество информации при пере­даче непрерывных сообщений, необходимо предварительно познако­миться с оценкой количества информации в дискретных сообщениях, т. е. в сообщениях об отдельных событиях или о дискретных состоя­ниях объектов. Информационные характеристики, найденные для диск­ретных сообщений, распространяются затем на непрерывные сообще­ния.

Количество информации в дискретных сообщениях. Пусть имеет­ся объект, способный принимать конечное число дискретных состоя­ний, пронумерованных числами от 1 до п. Предположим, что в сооб­щении о том, что объект находится в каком-то конкретном состоя­нии (i-м), содержится тем больше количества информации, чем бо­лее нее предел енными были сведения об объекте до получения сооб­щения, т. е. чем меньше была априорно известная получателю вероят­ность p_i того, что объект примет z'-e состояние. Итак, положим, что количество информации . в данном сообщении определяется ве­личиной 1 /р.. Далее установим, какой характер должна иметь зави­симость £j ■ от 1 /р.. Эту задачу решают на основе следующих сообра­жений.

Если некоторое сложное сообщение эквивалентно нескольким прос­тым, взятым вместе, то количество информации, содержащееся в сложном сообщении, должно быть равно сумме количеств информа­ции, содержащихся в каждом из простых сообщений. Поясним зто примером. Пусть одновременно рассматриваются два взаимно незави­симых объекта, каждый из которых может принять любое из п состоя­ний с равной вероятностью р - 1/и. Можно говорить о комбинации со­стояний обоих объектов. Число возможных комбинаций равно п², а ве­роятность любой из них р.. = 1/и². В сложном сообщении о том, что в

Ч

Данный момент имеет место определенная комбинация состояний двух объектов (одна из п² возможных), содержится столько же информа­ции, сколько в двух сообщениях: о том, что первый объект находит­ся в г-м состоянии, а второй — в /-м. Количество информации d _сп в сложном сообщении определяют величиной 1 /р_{. = и², а количество информации Cf в простом сообщении определяется величиной 1/р_} = ~ 1/р. = п. Требование

Cf , +Cf „ cs?n

сл npl np2

будет соблюдено только в том случае, если принять, что У в каждом сообщении пропорционально логарифму от 1/р.

=Ч_Р2 = !<* (1/р,) = i°e«;

^Jcn ^{= 1о}ё(1/Ру) ⁼ bgw²; ^Jnpl ^{+ J}n_V2 ^{= 21}°ё^{и =}

2 _

При этом коэффициент пропорциональности и основание логариф­ма могут бьггь любыми. Как будет показано далее, во многих случа­ях удобно пользоваться двоичными логарифмами, а коэффициент про­порциональности положить равным единице. Пока для рассматривае­мого примера убедимся, что условие (5.21) соблюдается независимо от основания логарифма. Действительно,

= 3 .

сл

Итак, количество информации в одиночном дискретном сообще­нии о событии, имеющем априорную вероятность р.,

J. = log (1/р.). (5.22)

Практически интересна не эта величина, а среднее количество ин­формации, приходящееся на одно сообщение, т. е.

■⁷= i Р: Cf = 2 в. log — = - £ рЛощ. (5.23)

i=l /=1 Р,- /=1

Здесь усреднение вьшолнено с учетом вероятности появления каж­дого из сообщений: количество информации в г-м сообщении умноже­но на весовой коэффициент р-.

Выражение в правой части (5.23) характеризует в усредненном виде неопределенность состояния данного' объекта. Эта величина на­зывается энтропией объекта. Ее принято обозначать буквой Н:

Н=- i p. logp.. (5.24)

i = 1

Для рассмотренного случая передачи сообщения получилось, что Cf ⁼ = Н. Но это равенство справедливо лишь в том случае, когда после полу­чения сообщения неопределенность сведений об объекте исчезает пол­ностью, т. е. когда каждое сообщение абсолютно достоверно. При­менительно к передаче информации зто означает, что сообщения не искажаются помехами и всегда воспринимаются получателем в таком 276

виде, в каком они были переданы. При зтом для получателя априорная вероятность того, что объект находится в i-м состоянии, равная р_{, а апостериорная вероятность этого же события после получения сооб­щения равна 1.

В общем случае нужно учитывать, что любое сообщение может быть искажено помехами и поэтому апостериорная вероятность пребы­вания объекта в i-м состоянии после получения сообщения меньше единицы. По-вццимому, получаемое при зтом количество инфор­мации меньше, чем в отсутствие помех. Обозначим передаваемые сообщения Xi, х₂, ..., x_f, ... х_п, а принимаемые у_у, у₂, ..., у., ..., у_т (в общем случае может быть т Ф п). Пусть было передано сообще­ние х_г-, а принято сообщение у_}-. Полученное при зтом частное (инди­видуальное) количество информации определим как

J(x_v У_}) = log |р (хр.)/р (х_г.)], (5.25)

где р (х•) — вероятность того, что было передано сообщение jr.;

pixPj) — условная вероятность того, что при получении сообщения

у . исходной его причиной была передача сообщения х- 7 '

По теореме Байеса, вероятность совместного наступления собы­тий x_f и у.

I J

p(x_r yj) = р(х.\У])р 0_;.) = р(у_}\х_{)р(х_{).

С учетом этого получим другое выражение, эквивалентное (5.25):

а(х_г У;) = 1оё[р(У;\Х.)1(р(у.)] . (5.26)

При отсутствии помех (искажений) передаче х. всегда соответст­вует приему, ат = п. При зтом р (х_;) = р 0_г-) = р_г-, р С*-!^-) = Р 0_г1*-)= = 1.

Тогда

3(Xj. У_{) = По­следовательно, формула (5.22) является частным случаем (5.25) и (5.26).

(5.27) 277

Среднее количество информации относительно передаваемых сооб­щений х, содержащееся в принимаемых сообщениях у, найдем, усред­нив .'/ (х.,у.) по всем возможным значениям i и/:

т п

у(х, у) = 2 2 р(х у) J (х_г у). ]= 1 i = 1

Здесь весовым коэффициентом при усреднении служит вероятность совместного наступления событий х_{, у., т. е. р(x_f, yj). Проведем не­которые преобразования:

J(x, у) = Г 2 p(x_v у.)log ^{Р (хЛу0} = ] i ' Р (х,)

= ЕЕр (х_;, у j) log р (х. | у j) - ES р (*_f, Уу) logp (х.) = / г / г

= 2 Р (уj) 2 р (Xj | Уу) log р (рс. | Уу) - 2 р (х.) log р (х.) Zp(y_f\x.).

j t ft i j

Сумма условных вероятностей р(у,-|х.) отвечает условию норми-

] I

рования,т. е.

2 р 0_;.|х.) = 1. i

Поэтому

:'/(х, у) = 2 p(yj) SpCx Iy^logpCx-lyp - / г"

- (x.)logp (x_f). i

Введем обозначение

Н(х|уу ) = — 2 р(*_г-1у_;) Iogp (х_г-|у_у). (5.28)

/

Эта величина представляет собой условную (апостериорную) энт­ропию передаваемых сообщений при приеме сообщения у.. Усредне­ние ее по всем возможным значениям у. дает среднюю условную (апостериорную) энтропию

Н(х\у) = 2р(у_/)Я(х|у_/). (5.29)

/

Величина

Н(х) = — 2 р (х_г) logр (х.) (5.30)

i

представляет собой безусловную (априорную) энтропию передавае­мых сообщений.

С учетом (5-28) - (5.30) получим

J(х, у) = Н(х) - Н(х\у). (5.₃₁)

Это означает, что в общем случае среднее количество информации относительно объекта, содержащееся в принятом сообщении, равно уменьшению средней неопределенности состояния объекта, т. е. раз­ности безусловной и условной энтропий.

Нетрудно убедиться, что в отсутствие помех (искажений) Н(х\у) = = 0. В этом случае, как показано ранее, условные вероятности равны 1. Учитывая, что log 1 = 0, придем к тому, что правые части формул (5.28) и (5.29) обращаются в нуль. Тогда среднее количество инфор­мации равно энтропии передаваемого сообщения. В общем случае Н(х\у) есть величина дезинформации, вносимой шумами.

Аналогичные преобразования можно провести, приняв за основу выражение (5.26). При зтом получим соотношение, симметричное (5.31):

J(x, у) = Н(у) - Н(у\х). (5.32)

Доказано,что всегда справедливо неравенство

J(x, у) > 0, (5.33)

т. е. среднее количество информации не может быть отрицательной величиной.

Этого нельзя сказать о частном количестве информации, получа­емой в результате однократной передачи. Значение С! (х_е yj) может ока­заться и отрицательным: дезинформация, внесенная помехами, мо­жет превысить информацию, которую несет переданное сообщение. Это бывает, когда передано X-, принято у. и при этом условная веро­ятность р (х_;| у.) меньше вероятности р (х).

Покажем, что применение двоичных логарифмов удобно при под­счете количества информации. Пусть объект имеет два возможных состояния. Тогда для передачи сообщений о состоянии объекта можно применить элементарный двухпозиционный сигнал. Если вероятнос­ти обоих состояний объекта равны между собой, т. е. р_{ = 1/2, то при пользовании двоичными логарифмами энтропия источника Н = 1. Этой же величине равно количество информации С/, если в канале нет по­мех. В данном случае один элементарный сигнал несет одну двоичную единицу информации.

С помощью к элементарных двоичных сигналов можно передать сообщения об объекте, имеющем 2^к возможных состояний. Если все эти состояния равновероятны, то каждое сообщение из к символов несет количество информации, равное к двоичным единицам. Этим объясняется удобство применения двоичных логарифмов.

Двоичная единица информации называется битом¹.

Количество информации в , непрерывных сообщениях. Рассмотрим информационные характеристики непрерывных сообщений. Если х непрерывна, она имеет бесконечное множество возможных значений. Введем для нее понятие энтропии с помощью предельного перехода.

Заменим бесконечное множество значений х некоторым числом ^значений, взятых через равные интервалы:

^Д* = (*кон - *на

гдех„„ их — начальное и конечное значения х.

НаЧ КОН

Для к-го значения измеряемой величины получим выражение х_к = = к Ах. Вероятность появления к-го значения находим из плотности распределения/^) по формуле p(x_k) ~ f(x_k)Ax.

Это выражение тем точнее, чем меньше Ах. Энтропия квантованной величины х *

Н(х*) = - Zp(x_k)logp (х_к) «-Е Axf(x_k)\og |f(x_k) Ах] =

к

= -Д* 2/(*_Л)1ов/(*_Л) - log Ах 2Дxf(x_k). к к

По условию нормирования

2Д xf(x_k) = 1.

к ^к

С учетом этого

#(¹) ~ -Д* log f(x_k) - log Ах.

к

При Ах -* 0 первое слагаемое обращается в - J f(x)\ogf(x)dx, но

х

второе стремится к бесконечности. Таким образом, предельный пере­ход пока не позволил нам ввести понятие энтропии непрерывного со­общения. Однако при определении количества информации для слу­чая, когда сигнал искажен шумами (помехами), нужно из безуслов­ной энтропии Н(х) вычесть среднюю условную Н(х\у). В этом слу­чае при квантовании* иу получается, что энтропии соответствующих кван­тованных величин Н(х*) и Н(х *|у *) имеют одинаковые составляю­щие — log Дх, которые при вычитаний взаимно компенсируются. Пре­дельный переход при Ах ->0 дает

J(x, У) = -Sf(x)logf(x)dx + x

+ Sf<y)Uf(x\y)logf(x\y)dx] dy. У *

Величину

Я_диф(х) = - j f(x) log f(x)dx (5.34)

x

назьшают априорной (безусловной) дифференциальной энтропией непрерывной величины х, а величину

^ЯдифС*1*) = -J/00[J/(x|y)log/(x|y)rfK] dy (5.35)

У *

— апостериорной (условной) дифференциальной энтропией.

Соответственно количество информации есть разность априорной и апостериорной дифференциальных энтропий

•^С*. >0 = "диф (х) - Я_диф (х|у). (5.36)

Аналогично можно получить выражение

У) = "диф О) - Я_диф (Их). (5.37)

Заметим, что дифференциальная энтропия зависит от того, в каких единицах выражена переменная. Разность энтропий не зависит от это­го, если только единицы одинаковы.

Вьюедем еще одно выражение для количества информации, отра­жающее симметричность этого критерия, т. е. то, что в величине у со­держится столько же информации о величине х, сколько в величине х о величине у. Как и в предыдущем случае, возьмем за основу соот­ношения, полученные для объектов с дискретными состояниями. Пре­образуем формулу (5.25), выражающую количество информации в одиночном сообщении при наличии помех. Умножим на p(yj) числи­тель и знаменатель дроби под знаком логарифма:

, Ур = log [р (х_{ | yj) р b>j)ip (х_г.) р О,-)] = = log [р (Х_{ , y_f)/p (X.)p (Vj)] .

Подставим полученное выражение в (5.27):

Ж у) = Е Ер(х_г-, y₇-)log [рЦ, у_})1р(х.)р(у_})]. j i

Далее найденную формулу применим к непрерывным величинам х и у, подвергнув их квантованию с шагом Ах = Ау, и совершим затем предельный переход при Ах ->0. Тогда получим

J(x, у) - И (X, j/)log [fix, y)lf(x)f(y)] dxdy. (5.38)

Во многих случаях принимаемую (воспроизводимую) величину у можно представить как сумму передаваемой (измеряемой) вели­чины х и некоторой помехи s:

У = х + s, (5.39)

причем помеха часто не зависит от х.

В этом случае условная дифференциальная энтропия #_диф (у|х) равна безусловной энтропии помехи #_ДИф (s). Покажем это. По ана­логии с (5.35)

^Ядиф01*) = - f f(x)[S f(y\x)logf(y\x)dy] dx. (5.40)

x у

Рассмотрим выражение в квадратных скобках под интегралом в правой части (5.40). Заменим переменную .у в соответствии с (5.39). При этом dy = ds. Будем иметь в виду, что данный интеграл вычисля­ется для фиксированного значения х:

S f(y\x)logf(y\x)dy = //(х + s|x)log/(x + s|x)rfs.

у s

Если значение х фиксировано, то условная вероятность обращает­ся в безусловную, т. е./(х + s|x) =/(s). Следовательно,

J/(x + s|x)log/(* + s\x)ds = //(s)log/(s)ds = - #_диф(5). s s

Тогда

Интеграл в правой части последнего выражения равен 1, поэтому

Формулу (5.37) с учетом (5.41) приведем для рассматриваемого случая к виду

•Ж У) = "дифОО - ^Ядиф • (⁵-⁴²>

Предполагаем, что при вычислении обеих энтропии — принимаемо­го сигнала и помехи — величины у и s выражаются в одинаковых еди­ницах.

Если измеряемая величина х и помеха s имеют нормальные распре­деления, то их сумма также имеет нормальное распределение. Диф­ференциальная энтропия нормально распределенной величины х, вы­численная по (5.34),

^Ядиф(^х> = (l/2)log [2neD (х)],

где D(x) — дисперсия величины х. Соответственно

Я_диф(у) = (l/2)log [2тeD (у)] = (1/2) log { 2тге [D(x) + D(s)] } ; Н ЛЛ = /OMi-.tr ГСя-оПЛМ

(5.43)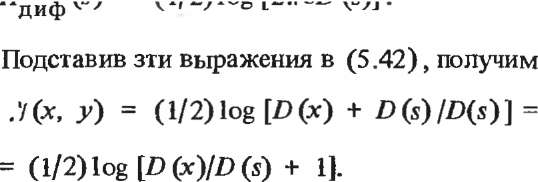

Как известно, дисперсия сигнала пропорциональна его средней мощ­ности, которую обозначим Р . Среднюю мощность помехи обозначим P_s. Тогда

«У(х, У) = (1/2) log(P_x/P_s + 1).

Напомним, что зта формула справедлива для случая, когда помеха^ является аддитивной и не зависит от сигнала, а законы их распределе­ния — нормальные.

(5.44)

До сих пор не учитывалось, что х есть функция времени, между тем рассматривалась передача отдельных сообщений о значениях не­которой непрерывной величины х. При этом величина J (х, у) трак­товалась как среднее количество информации, содержащееся в одном принятом значении у. Подразумевалось, что усреднение проводится по множеству всех возможных значений х и у с учетом законов рас­пределения каждой из величин отдельно и обеих вместе.

Теперь перейдем к рассмотрению передачи случайной функции вре­мени х (/) по каналу, в котором действует случайный шум s (t). Пусть частотный спектр процесса x(t) ограничен частотой / . Согласно тео­реме Котельникова (см. § 5.2) указанный процесс x(t) полностью определяется последовательностью ординат, взятых с интервалом Т =

= 1/2/,

В среднем передача значения одной ординаты приносит получате­лю информацию, равную ,7 (х, у). Это происходит каждые Т секунд. Значит, в единицу времени передается в среднем количество инфор­мации

С = ,У(х, у)/Т = 2f_rp3(x, у). (5.45)

Величина С называется средней скоростью передачи информации.

При независимом аддитивном шуме s(t) и нормальных распреде­лениях х и s средняя скорость передачи информации

С = f_rplog(P_xIP_s + 1). (5.46)

Связь между информационными и точностными характеристиками.

Информационные Критерии применимы не только к системам переда­чи информации, но и к измерительным приборам и системам. Погреш­ность Д есть помеха, вносящая дезинформацию. При аддитивной неза­висимой погрешности Д справедливо соотношение, аналогичное (5.42):

3 (^х> У) ^{= Я}дифО) -"„_Иф(Д). (⁵-47)

где 3 (х, j) — среднее количество информации, получаемое при од­ном измерении величины х; #д_Иф0О ^{и Я}_ДИф (Л) — дифференциаль­ные энтропии воспроизводимой величины и погрешности.

Если к тому же измеряемая величина х и погрешность Д имеют нор­мальные распределения, то количество информации можно выразить через дисперсии этих величин по аналогии с (5.43) :

9{х, у) = - log [D(x)/D (Д) + 1]. (5.48)

2

Рассматривая измеряемую величину как случайную функцию вре­мени, можем определить среднюю скорость получения информации при измерении по (5.45). Если при этомх и Д — взаимно независимые величины с нормальными распределениями, то

С = /_грlog [D (x)/D (Д ) + 1]. (5.49)