768

Раздел 9. Применение математических методов в биологии и геологии 750

ЛЕКЦИЯ 9.1. ПРИМЕНЕНИЕ МАТРИЧНЫХ МЕТОДОВ В БИОЛОГИИ. БИОЛОГИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ БИОЛОГИЧЕСКИХ СИСТЕМ 750

9.1.1. Дифференциальные уравнения в математическом моделировании биологических систем 750

ЛЕКЦИЯ 9.2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ГОРНО-ГЕОЛОГИЧЕСКИХ ЗАДАЧАХ 757

9.2.1. Общий подход к составлению математической модели 757

9.2.2. Решение одной технической задачи 757

9.2.3. Моделирование процессов при помощи дифференциальных уравнений 759

9.2.4. Решение задач горно-геологического профиля средствами теории вероятности и математической статистики 762

Контрольные вопросы и задания для самопроверки. 767

РАЗДЕЛ 9. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ В БИОЛОГИИ И ГЕОЛОГИИ

ЛЕКЦИЯ 9.1. ПРИМЕНЕНИЕ МАТРИЧНЫХ МЕТОДОВ В БИОЛОГИИ. БИОЛОГИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ БИОЛОГИЧЕСКИХ СИСТЕМ

Вспомним, какова принципиальная схема большинства биологических открытий. Интересующее нас явление многократно повторяется в разных условиях: меняется температура, давление, освещенность и т.д. Результаты наблюдений и условия опытов фиксируются в виде таблиц, схем, графиков. Как осмыслить полученную информацию, как отделить случайное от неслучайного, как поймать в этом множестве данных характерную особенность изучаемого явления? Без математической обработки результатов эксперимента здесь не обойтись. В результате такой обработки возникает экспериментальный (эмпирический) закон. Яркими примерами таких открытий, полученных в результате статистического анализа, является закон Г.Менделя, биогенетический закон, простой закон увеличения численности популяций. Однако, у экспериментальных законов есть существенный недостаток: говоря обыденным языком, они отвечают на вопрос «как?» и, как правило, не отвечают на вопрос «почему?». Возможности прогнозирования с помощью экспериментальных законов ограничены. Не зная внутренней механики процесса, не умея ответить на вопрос, почему он развивается таким, а не иным образом, мы не можем предсказать, как мог бы идти процесс в условиях, отличных от условий нашего опыта.

Итак, необходимо знание закономерностей, охватывающих широкий класс родственных явлений и отвечающих на вопрос «почему?».

Большую роль в установлении таких законов играют математические методы. Это применение математики в биологии существенным образом отличается от обработки результатов. Ведь речь идет о принципиально новом построении исследования, о математическом образе мышления при решении биологической проблемы, о математическом моделировании. Примеры такого моделирования мы и рассмотрим в сегодняшней лекции.

9.1.1. Дифференциальные уравнения в математическом моделировании биологических систем

Рассмотрим простую модель роста популяции. Если необходимые для популяции ресурсы имеются в изобилии, то естественно предположить, что скорость роста будет пропорциональна размеру популяции. Если соответствует популяции в момент времени , то такое предположение выражается дифференциальным уравнением

, (9.1.1)

где – постоянная. Предположение, приводящее к этому уравнению, состоит в том, что скорость роста на единицу популяции (удельная скорость роста) постоянна, т.е. .

Решая это линейное дифференциальное уравнение первого порядка, получаем . Если размер популяции в некоторый момент времени известен, то постоянную в решении можно определить единственным образом. Тогда решение примет вид

. (9.1.2)

Решение (9.1.2) представляет собой формулу экпоненциального роста. Если , то популяция с течением времени возрастает; если , то она остаётся на постоянном уровне; если , то популяция убывает со временем до нуля.

Пример 1. Найти решение дифференциального уравнения , удовлетворяющее начальному условию . Если обозначает размер популяции бактерий после часов роста, то чему равен размер популяции спустя 10 часов?

Решение. Общее решение уравнения имеет вид . Решением, удовлетворяющим заданному начальному условию, является . После 10 часов роста размер популяции становится равным .

Пример 2. Популяция бактерий увеличивается таким образом, что удельная скорость роста в момент (время выражается в часах) составляет величину . Допустим, что начальной популяции соответствует . Какой будет популяция после четырех часов роста и после двенадцати часов роста?

Решение. Удельная скорость роста равна . Это однородное линейное уравнение первого порядка. Интегрируя его, получаем , где – постоянная интегрирования. Отсюда . Поскольку, , имеем , и искомое решение имеет вид . Следовательно, размер популяции после четырех часов роста будет равен . Спустя двенадцать часов популяция вырастет до .

Рассмотрим модель сезонного роста. Дифференциальное уравнение первого порядка , где – положительная постоянная, можно рассматривать как простую модель сезонного роста. Скорость роста популяции становится то положительной, то отрицательной, и популяция то возрастает, то убывает. Это может вызываться такими сезонными факторами, как доступность пищи. Интегрируя данное уравнение, получаем общее решение в виде .

Следующая модель, доступная нашему рассмотрению – внутривенное питание глюкозой. Вливание глюкозы в кровеносную систему является важной лечебной процедурой. Для изучения этого процесса определим как количество глюкозы в крови пациента в момент времени . Допустим, что глюкоза вводится в кровь с постоянной скоростью (г/мин). В то же время глюкоза разлагается и удаляется из кровеносной системы со скоростью, пропорциональной имеющемуся количеству глюкозы. Таким образом, функция удовлетворяет дифференциальному уравнению , где – положительная постоянная. Это неоднородное линейное дифференциальное уравнение первого порядка. Интегрируя его, получаем . Постоянную можно выразить через начальное количество глюкозы в крови . Получим . Значит, общее решение может быть записано в виде . С увеличением времени приближается к пределу, равному . Это и есть равновесное количество глюкозы в крови.

Модель логистического роста. Скорость роста популяции в расчете на одну особь представляет собой разность между средней рождаемостью и средней смертностью. Будем считать, что средняя рождаемость выражается положительной постоянной , не зависящей от времени и размера популяции . Допустим также, что средняя смертность пропорциональна размеру популяции и потому равна , где – положительная постоянная. Это увеличение смертности с ростом популяции может происходить благодаря эффектам скученности или усиливающейся конкуренции за доступные пищевые ресурсы. В данной модели уравнение, которому подчиняется рост популяции, имеет вид или . Разделяя переменные, получаем . Так как , то, интегрируя, получим . Таким образом, . Если – размер начальной популяции, тогда . После преобразований получаем . Процесс роста, описываемый такой функцией, называется логистическим ростом, а исходное дифференциальное уравнение – логистическим. При логистическом росте популяция с увеличением времени приближается к предельному равновесному состоянию, равному . Следовательно, размер популяции прямо пропорционален средней рождаемости и обратно пропорционален средней смертности на одну особь.

Рассмотрим несколько моделей, описываемых системами дифференциальных уравнений.

Модель межвидовой конкуренции. Взаимное влияние популяций двух конкурирующих видов на скорости их роста описывает однородная линейная система . Допустим, что начальные популяции насчитывают и особей. Решая систему методом исключения, получаем , где – постоянные. Воспользовавшись начальными условиями, получаем и . Следовательно, искомое решение есть , . Вымирание первого вида происходит, когда , т.е. при единиц времени. По прошествии этого времени второй вид продолжает расти согласно уравнению . Общее решение этого уравнения показывает рост популяции второго вида после вымирания первого.

Модель взаимодействия «хищник – жертва».

Пусть функция соответствует численности вида-хищника, а – численности вида-жертвы. Предположим далее, что скорости роста их популяций описываются линейной системой Требуется определить численность популяций во все последующие моменты времени, если начальная численность популяций составляет особей. Когда наступит вымирание вида-жертвы?

Используя метод исключения, получаем общее решение системы: и . Начальные условия дают . Искомое решение системы есть , . Популяция жертв вымирает, когда , т.е. после единиц времени. Популяция хищников продолжает расти за счет других ресурсов среды и описывается уравнением . Часто, однако, бывает, что допущения, сделанные при построении модели взаимодействия видов, теряют справедливость после исчезновения одного из видов.

Модель кооперации видов (симбиоза).

Допустим, что два вида находятся в отношениях симбиоза, т.е. популяция каждого вида возрастает пропорционально численности другого, а уменьшение популяций каждого вида будем считать пропорциональным собственной численности. Моделью такого поведения популяций может служить линейная система .

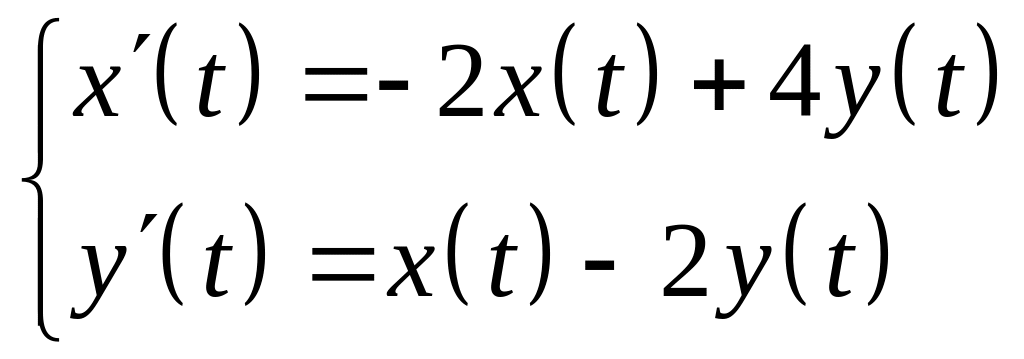Требуется найти численности видов во все последующие моменты времени, если начальные популяции насчитывают и особей.

Методом исключения находим общее решение системы и . Используя начальные условия, находим и . Искомое решение есть и . Следовательно, популяция первого вида возрастает от первоначального размера в 100 особей до предельного размера в 350 особей. Второй вид убывает от первоначального размера в 300 особей до предельного размера в 175 особей. Эти предельные размеры соответствуют равновесным популяциям двух видов, которые могут поддерживаться в данной среде.

Вернемся к уравнению (1), описывающему простую модель роста популяции. Более точное описание развития популяции дает уравнение Ферхюльста–Перла, полученное в 1845 году. Оно учитывает так называемый эффект «самоотравления» популяции или, попросту говоря, внутривидовую борьбу (конкуренция за место обитания, пищу, тесноту, распространение инфекций, и т.п.). Желая учесть этот эффект, мы должны при подсчете прироста численности популяции от величины вычесть некоторую величину ,такую, что , где функция для многих популяций может быть взята в виде произведения , где . Величина отражает снижение скорости роста из-за внутривидовой конкуренции. Но конкуренция тем выше, чем больше количество встреч между особями, а количество встреч пропорционально произведению на , т.е. . Итак, окончательно, . Здесь – коэффициент, характеризующий рождаемость. Разделив это равенство на и переходя к пределу при , стремящемся к 0, получаем , где положительны. Разделяя переменные и интегрируя, получаем . Далее, . Откуда или . Выражая отсюда , окончательно получаем . Величина имеет определенный биологический смысл – это максимальная численность популяции, теоретически возможная в данных условиях.

Мы рассмотрели далеко не все математические модели, применяемые к исследованиям в области биологии. Завершить лекцию хотелось бы высказыванием из «Теоретической биологии» Э.С.Бауэра: «Теоретическая обработка какого-либо явления заключается именно в том, что мы из большого многообразия специальных конкретных явлений абстрагируем общее закономерное и исследуем эту отвлеченную закономерность, анализируем и выявляем её различные формы. Мы допускаем определенные условия и определяем, как процесс должен протекать при данных условиях. Мы сравниваем полученный таким образом результат с данными опыта… и исследуем, действительно ли протекает процесс так, как мы это вывели из абстрагированного нами общего закона. Если полученный таким образом абстрагированный общий закон действительно оправдается, т.е. если на опыте или в эксперименте подтверждаются сделанные из него выводы…, то мы можем при его помощи… предсказать ход процессов. Тогда этот абстрактный общий закон сделается достоянием теоретической науки».