482

Раздел 4. Дифференциальные уравнения 411

ЛЕКЦИЯ 4.1. ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ 411

4.2.1. Уравнение, не содержащее искомой функции 419

4.2.2. Уравнение, не содержащее независимой переменной 420

4.2.3 Уравнение с разделяющимися переменными 421

4.2.4. Однородное уравнение 423

4.2.5. Простейшее уравнение, приводящееся к однородному 425

ЛЕКЦИЯ 4.3. ЛИНЕЙНОЕ УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА. МЕТОД ВАРИАЦИИ ПРОИЗВОЛЬНОЙ ПОСТОЯННОЙ (МЕТОД ЛАГРАНЖА). УРАВНЕНИЕ БЕРНУЛЛИ 427

4.3.1. Линейное уравнение 427

4.3.2. Метод вариации произвольной постоянной (метод Лагранжа) 432

4.3.3. Уравнение Бернулли 434

ЛЕКЦИЯ 4.4. УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ. УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. 437

4.4.1. Уравнения в полных дифференциалах 437

4.4.2. Уравнения высших порядков. Основные понятия и определения 440

ЛЕКЦИЯ 4.5. УРАВНЕНИЯ, ИНЕГРИРУЕМЫЕ В КВАДРАТУРАХ И УРАВНЕНИЯ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА 446

4.5.2. Уравнение, не содержащее искомой функции и последовательных первых производных 448

4.5.3. Уравнение, не содержащее независимой переменной 448

ЛЕКЦИЯ 4.6. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ n-ГО ПОРЯДКА 451

4.6.1. Основные понятия и определения 451

4.6.2. Однородное линейное уравнение n-го порядка 452

4.6.3. Неоднородные линейные уравнения 455

4.6.4. Метод вариации произвольных постоянных (метод Лагранжа) 456

ЛЕКЦИЯ 4.7. ЛИНЕЙНЫЕ УРАВНЕНИЯ n-ГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 459

4.7.1. Однородное уравнение 459

4.7.1.1. Построение фундаментальной системы решений и общего решения однородного линейного уравнения в случае различных корней характеристического уравнения 459

4.7.1.2. Случай наличия кратных корней характеристического уравнения 461

4.7.2. Неоднородное уравнение 463

4.7.2.1. Нахождение частного решения неоднородного уравнения методом неопределенных коэффициентов 464

ЛЕКЦИЯ 4.8. СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 467

4.8.1. Основные понятия и определения 467

4.8.2. Линейные системы дифференциальных уравнений 470

4.8.2.1. Однородные линейные системы 470

4.8.2.2. Неоднородные линейные системы 473

4.8.2.3. Метод вариации произвольных постоянных (метод Лагранжа) 475

4.8.3. Линейные системы дифференциальных уравнении с постоянными коэффициентами 476

Контрольные вопросы и задания для самопроверки 482

Раздел 4. Дифференциальные уравнения лекция 4.1. Введение. Основные понятия

^{Определение 1. Обыкновенным дифференциальным уравнением n-го порядка называется соотношение вида}

^{F(x,y,y,y,…y(n))=0, (4.1.1)}

^{где F – известная функция своих аргументов, заданная в некоторой области; x – независимая переменная; y – функция переменной x, подлежащая определению; y,y,y,…y(n) – ее производные.}

^{При этом предполагается, что y(n) действительно входит в соотношение (4.1.1), любой же из остальных аргументов функции F может в этом соотношении явно и не участвовать.}

^{Определение 2. Соотношение аналогичное (4.1.1) связывающее независимые переменные x}₁^{, x}₂^,...,x_n^{, функцию этих переменных и ее частные производные по переменным x}₁^{, x}₂^,...,x_n ^{до порядка n включительно, называется уравнением с частными производными n-го порядка.}

^{Определение 3. Всякая функция, определенная вместе с соответствующими производными (до порядка n) в некоторой области, называется решением дифференциального уравнения в этой области, если она обращает его в тождество, справедливое для всех точек упомянутой области. В частности, y = y(x) будет решением уравнения (4.1.1) в интервале (a, b), если}

^{F(x, y(x), y'(x), .... y(n)(x))  0 (x  (a, b)). (4.1.2)}

^{Процесс нахождения решений называется интегрированием дифференциального уравнения.}

К дифференциальным уравнениям приводят многие задачи из механики, физики, астрономии и других естественных наук а также многие проблемы техники. Вообще обыкновенное дифференциальное уравнение может быть получено часто из физических или геометрических соображений, либо формально исключением параметров из уравнения n-параметрического семейства функций и n равенств, полученных из него последовательным дифференцированием.

Если мы сумеем проинтегрировать полученное дифференциальное уравнение, то тем самым дадим ответы на вопросы задачи, которая привела нас к этому уравнению.

Поэтому основной задачей теории интегрирования дифференциальных уравнений является нахождение всех решений данного дифференциального уравнения и изучение свойств этих решений.

Исключительно большой интерес как для самой теории дифференциальных уравнений, так и для ее многочисленных приложений представляет задача нахождения, или хотя бы доказательство, существования решения, удовлетворяющего заданным условиям.

Заметим, что саму задачу интегрирования дифференциального уравнения можно понимать по-разному. В самой узкой постановке задачи ставится целью выражение искомых функций через элементарные. Эта задача, вообще говоря, не разрешима даже для самого простого уравнения y=f(x) ибо, как известно, не всегда первообразная элементарной функции представляет собою тоже элементарную функцию. Поэтому под символом мы будем понимать какую-нибудь фиксированную первообразную, а постоянную интегрирования будем писать отдельно.

В дальнейшем будет показано, что большое количество уравнений удается проинтегрировать в квадратурах. При этом под интегрируемостью данного уравнения в квадратурах надо понимать представление решения в виде интегралов от элементарных функций и функций, входящих в уравнение.

Однако следует отметить, что уравнения, интегрируемые в квадратурах, составляют лишь незначительную часть всех дифференциальных уравнений.

Задача общей теории дифференциальных уравнений состоит в изучении свойств функций, определяемых дифференциальными уравнениями непосредственно по виду любого заданного дифференциального уравнения, независимо от интегрируемости последнего в элементарных функциях или в квадратурах.

В соответствии со сказанным выше, уравнение первого порядка имеет вид

F(x,y,y)=0 (4.1.3)

Будем предпологать что это уравнение, разрешимо относительно производной

(4.1.4)

Наряду с этим уравнением мы часто будем рассматривать перевернутое уравнение

(4.1.4)

используя последнее в окрестности тех точек, в которых f(x, y) обращается в бесконечность.

Во многих случаях оказывается целесообразным вместо уравнений (4.1.4) и (4.1.4) рассматривать одно равносильное им дифференциальное уравнение

. (4.1.5)

Обе переменные x и y входят в это уравнение уже равноправно, и любую из них мы можем принять за искомую переменную.

Умножая обе части уравнения (4.1.5) на некоторую функцию N(x,y), получаем более симметричное уравнение:

M(x, y)dx + N(x, y)dy = 0, (4.1.6)

где M(x, y)=  f(x,y)N(x,y). Обратно, всякое уравнение вида (4.1.6) можно переписать в виде уравнений (4.1.4) или (4.1.4'), разрешая его относительно или , так что уравнение (4.1.6) равносильно следующим двум уравнениям:

(N(x,y)≠0) и 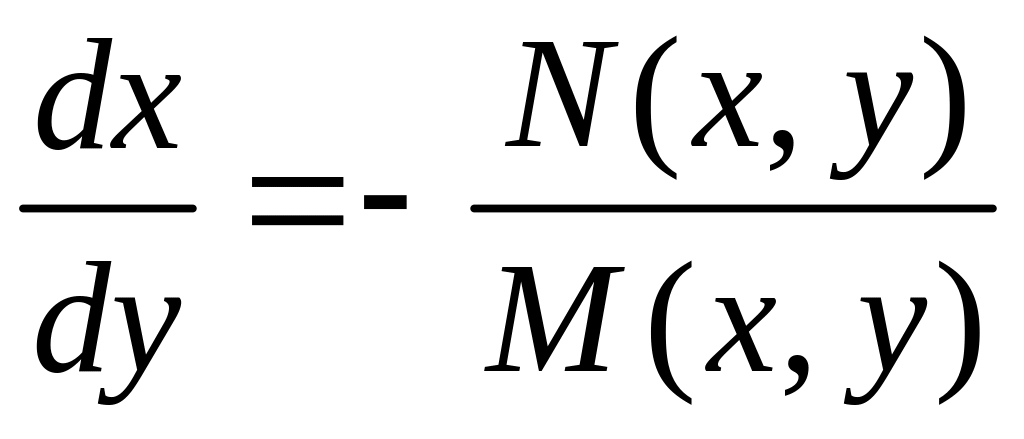(M(x,y)≠0). (4.1.7)

Предположим, что правая часть уравнения (4.1.4), f(x,y), определена на некотором подмножестве A вещественной плоскости (x,y).

Определение 4. Функцию y = y(x), определенную в интервале (a,b), мы будем называть решением уравнения (4.1.4) в этом интервале, если:

1. Существует производная y(x) для всех значений х из интервала (a,b). (Отсюда следует, что решение y = y(x) представляет собою функцию, непрерывную во всей области определения).

2. Функция y = y (x) обращает уравнение (4.1.4) в тождество:

y(x)  f(x, y(x)), (4.1.8)

справедливое для всех значений x из интервала (a,b). Это означает, что при любом x из интервала (a,b) точка [x, y(x)] принадлежит множеству A и y(x)=f(x, y(x)).

Так как наряду с уравнением (4.1.4) рассматривается перевернутое уравнение (4.1.4'), то и решения x = x(y) этого перевернутого уравнения естественно присоединять к решениям уравнения (4.1.4).

Иногда функцию y = y(x), обращающую уравнение (4.1.4) в тождество (4.1.8), т. е. решение уравнения (4.1.4), называют интегралом этого уравнения.

Далеко не всегда удается получить решение дифференциального уравнения в явном виде. Кроме того, явное задание решения и не всегда удобно для его изучения и использования. Поэтому при интегрировании уравнения во многих случаях удовлетворяются получением решения в неявном виде.

Определение 5. Уравнение

(x,y)=0 (4.1.9)

определяет в неявной форме решение уравнения (4.1.4), если оно определяет y как неявную функцию от x, y = y(x), и если эта последняя является решением уравнения (4.1.4).

В этом случае, полагая в (4.1.9) y = y(x), дифференцируя полученное тождество по x и заменяя на f(x,y), приходим к равенству

, (4.1.10)

которое должно выполняться тождественно в силу соотношения (4.1.9).

Иногда, решение уравнения (4.1.4) получается в параметрической форме.

Определение 6. Уравнения

x=(t), y=(t). (4.1.11)

определяют решение уравнения (4.1.4) в параметрической форме в интервале (t₀, t₁), если в этом интервале имеет место тождество:

. (4.1.12)

Пример. Уравнения

x=acost, y=bsint

определяют решение уравнения

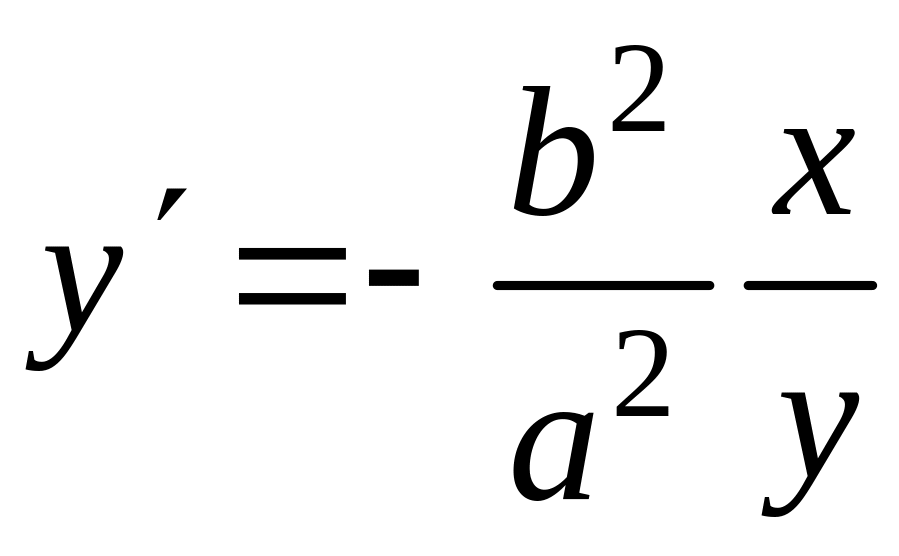
в интервале [0,2], ибо в этом интервале имеет место тождество

.

(Для t=0, t= и t=2 нужно рассматривать перевернутое тождество, соответствующее перевернутому уравнению )

Одной из важнейших задач в теории дифференциальных уравнений является так называемая задача Коши. Для уравнения (4.1.4)

,

задача Коши, или начальная задача, ставится следующим образом: среди всех решений уравнения (4.1.4) найти такое решение

y = y(x) (4.1.13)

в котором функция y(x) принимает заданное числовой значение y₀ при заданном числовом значении x₀ независимой переменной x, т.е.

y(x₀)=y₀, (4.1.14)

где x₀ и y₀ – заданные числа, так что решение удовлетворяет условию:

y = y₀ при x = x₀. (4.1.15)

При этом число y₀ называется начальным значением искомой функции, а число x₀ – начальным значением независимой переменной. В целом же числа x₀ и y₀ называются начальными данными решения (4.1.13), а условие (4.1.15) – начальным условием этого решения.

Вопрос о единственности решения задачи Коши представляет исключительный интерес как для самой теории дифференциальных уравнений, так и для ее многочисленных приложений, ибо, зная, что решение задачи Коши единственно, мы, найдя решение, удовлетворяющее заданным начальным условиям, уверены, что других решений, удовлетворяющих тем же начальным условиям, нет. В вопросах естествознания это приводит к тому, что мы получаем вполне определенный, единственный закон явления, определяемый только дифференциальным уравнением и начальным условием.

Поставим вопрос: каким условиям достаточно подченить правую часть уравнения (4.1.4) в окрестности начальных данных x₀ и y₀ чтобы решение задачи Коши удовлетворяющее начальным условиям (4.1.15) было единственным. На этот вопрос отвечает следующая теорема (теорема Пикара)

Теорема. Пусть дано уравнение

и поставлено начальное условие

y = y₀ при x = x₀

Предположим, что функция f(x,y) определена в некоторой замкнутой ограниченной области

R: ,

с точкой (x₀,y₀) внутри (а и b – заданные положительные числа) и удовлетворяет в ней следующим двум условиям:

1. Функция f(x,y) непрерывна и, следовательно, ограничена, т.е.

, (4.1.16)

где M – постоянное положительное число, (x,y) – любая точка области R;

2. Функция f(x,y) имеет ограниченную частную производную по аргументу y, т.е.:

, (4.1.17)

где K – постоянное положительное число, (x,y) – любая точка области R.

При этих предположениях уравнение (4.1.4) имеет единственное решение y=y(x), удовлетворяющее начальному условию (4.1.15). Это решение определено и непрерывно дифференцируемо в некоторой окрестности начального значения x₀ независимой переменной x, а именно оно заведомо определено в интервале

, (4.1.18)

где h есть наименьшее из чисел a и ,

. (4.1.19)

Дадим определение общего решения уравнения (4.1.4) в некоторой области D изменения переменных x,y (формулировка этого определения пренадлежит Н.П. Еругину). В качестве области D мы будем рассматривать некоторую область на плоскости (x,y), в каждой точке которой имеет место условие существования и единственности решения задачи Коши для уравнения (4.1.4). При этом область D есть либо все множество точек существования и единственности решения задачи Коши для уравнения (4.1.4), либо его часть.

Определение 7. Функцию y=(x,C), определенную в некоторой области изменения переменных x и C, имеющую непрерывную частную производную по независимой переменной x, будем называть общим решением уравнения (4.1.4) в области D, если равенство y=(x,C) разрешимо относительно произвольной постоянной C в области D, так что при любых значениях x и y, пренадлежащих области D, этим равенством определяется значение C по формуле

C=(x,y) (4.1.20)

и, если функция y=(x,C) является решением уравнения (4.1.4) при всех значениях произвольной постоянной C, доставляющих формулой (4.1.20), тогда точка (x,y) пробегает область D.

Пример. Рассмотрим уравнение . Покажим, что y=Cx (x0) является общим решением этого уравнения в области

0<x<, <y<.

Прежде всего в этой области имеет место существование и единственность решение задачи Коши (это следует из того, что правая часть уравнения непрерывна относительно x и y в этой области и в окрестности каждой точки из этой области ее частная производная по y ограничена). Далее уравнение y=Cx (x0) разрешимо в этой области относительно C и наконец, очевидно, что функция y=Cx (x0) является решением уравнения при всех значениях C. Следовательно, y=Cx (x0) есть общее решение уравнения в области 0<x<, <y<.

Определение 8. Общее решение (однопараметрическое семейство интегральных кривых) в неявном виде (в виде не разрешенном относительно y):

(x,y,C)=0 (4.1.21)

или

(x,y)=C (4.1.21)

называют общим интегралом уравнения (4.1.4) в области D, если эти соотношения определяют общее решение уравнения (4.1.4) в области D.

Определение 9. Семейство интегральных кривых, зависящее от одной произвольной постоянной C, в параметрическом виде:

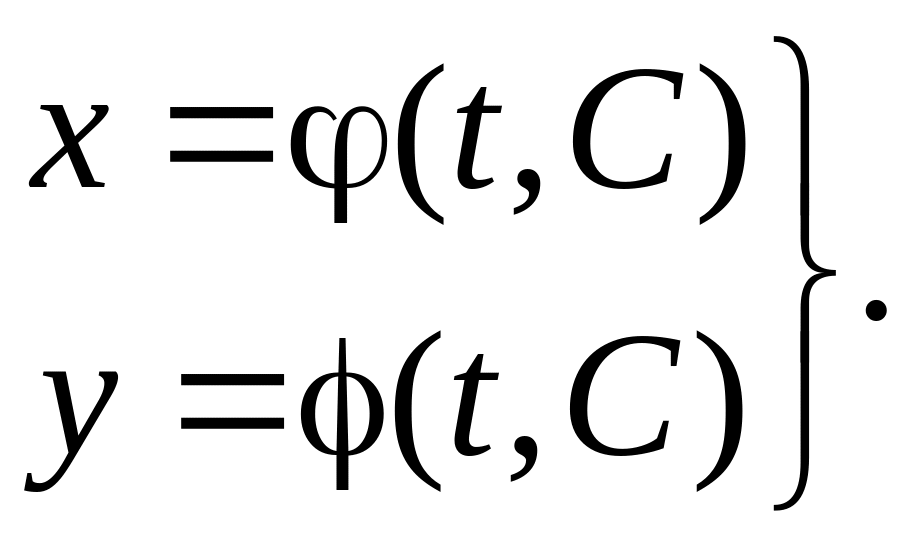(4.1.22)

будем называть общим решением уравнения (4.1.4) в параметрической форме.

Если из уравнения (4.1.22) удается исключить параметр t, то получают общее решение в неявном или даже в явном виде.

Пример. Уравнение

,

имеет следующее общее решение в параметрической форме:

Исключая параметр t, получим общий интеграл:

x²+y²=C².

Определение 10. Если решение уравнения (4.1.4) состоит из точек единственности решения задачи Коши для этого уравнения, то такое решение называется частным решением.

Таким образом любое решение определяемое теоремой Пикара является частным решением, ибо в каждой точке этого решения имеет место единственность решения задачи Коши для данного уравнения.

Определение 11. Решение в каждой точке которого нарушается единственность решения задачи Коши, называют особым решением.

Геометрически особому решению соответствует интегральная кривая, не содержащая в семействе интегральных кривых, состовляющих общее решение (общий интеграл). Поэтому особое решение не может лежать внутри области D существования общего решения.

Особое решение очевидно, не содержится в формуле общего решения ни при каком числовом значении произвольной постоянной C.

Пример. Возьмем уравнение . Здесь радикал берется с положительным знаком. Считая, что y0, делим обе части уравнения на . Получим:

или .

Отсюда

,

где x>C, так как x+C>0. Следовательно, уравнение имеет общее решение вида:

y=(x+C)², xC.

Очевидно, что решением данного уравнения будет также y0 (ось Ox). Это решение особое, так как во всех точках его нарушается единственность решения задачи Коши.

ЛЕКЦИЯ 4.2. НЕПОЛНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ. ОДНОРОДНЫЕ УРАВНЕНИЯ