
- •Определители. Свойства определителей Основные теоретические сведения
- •Основные свойства определителей
- •Приведение определителя к треугольному виду
- •Решение систем уравнений с помощью определителей (по формулам Крамера) Основные теоретические сведения
- •Матрицы. Операции над матрицами Основные теоретические сведения
- •Операции над матрицами
- •Многочлены от матриц
- •Обратная матрица
- •Решение систем алгебраических уравнений методом гаусса Основные теоретические сведения
- •Метод Гаусса. Схема с выбором главного элемента
- •Собственные векторы и собственные значения линейного преобразования Основные теоретические сведения
- •Квадратичные формы
- •Кривые и поверхности второго порядка Основные теоретические сведения
- •Список литературы
- •Оглавление
Собственные векторы и собственные значения линейного преобразования Основные теоретические сведения
Определение.
Ненулевой вектор
![]() ,
удовлетворяющий условию
,
удовлетворяющий условию
![]() ,
называется собственным вектором
преобразования
,
называется собственным вектором
преобразования
![]() .
Число
– собственное значение этого
преобразования, причем собственный
вектор
соответствует собственному значению
.
.
Число
– собственное значение этого
преобразования, причем собственный
вектор
соответствует собственному значению
.
Между
всеми линейными преобразованиями
пространства
![]() и всеми квадратными матрицами порядка
существует взаимно-однозначное
соответствие, зависящее от выбранного
в пространстве
базиса
и всеми квадратными матрицами порядка
существует взаимно-однозначное
соответствие, зависящее от выбранного
в пространстве
базиса
![]() .
Говорят, что матрица
.
Говорят, что матрица
![]() ,
,
![]() задает линейное преобразование
в базисе
задает линейное преобразование
в базисе
![]() ,
если
,
если
![]() .
.
Определение.
Определитель
![]() называется характеристическим многочленом
матрицы
:
называется характеристическим многочленом
матрицы
:
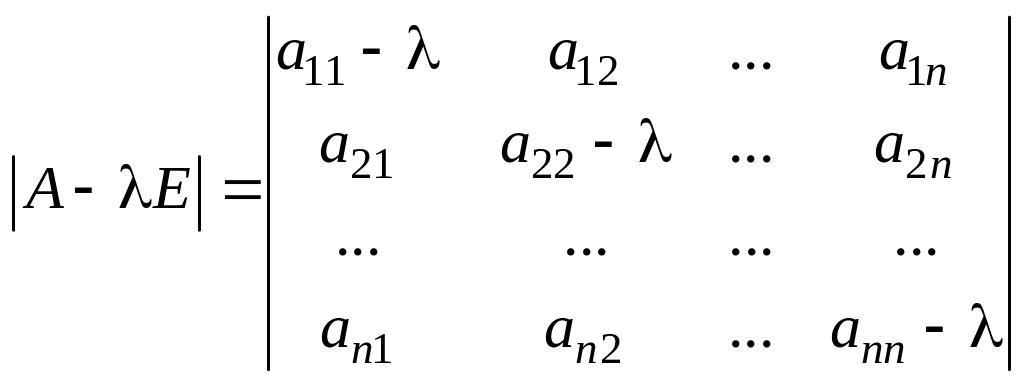 ,
,
а его корни – характеристическими корнями.
Характеристические корни линейного преобразования являются собственными значениями этого преобразования.
Примеры решения задач
Задача 1. Найти собственные значения и собственные векторы матрицы:
1)
![]() .
.
Решение.
Составим
характеристическое уравнение
![]() или
или
![]() ;
;
![]() .
.
Собственные
значения
![]() ;
;
![]() .
.
Найдем
собственный вектор:
![]()
При
![]()
![]()
![]() .
.
Следовательно,
решение этой системы
![]() ;
;
![]() .
Собственный вектор
.
Собственный вектор
![]() .
.
Пусть
![]() ,
тогда собственный вектор
,
тогда собственный вектор
![]() .
.
При система примет вид
![]()
![]() .
.
Решение
системы:
![]() ,
,
![]() .
Собственный вектор
.
Собственный вектор
![]() при
имеет вид
при
имеет вид
![]() .
.
Ответ. , ; ; .
2)
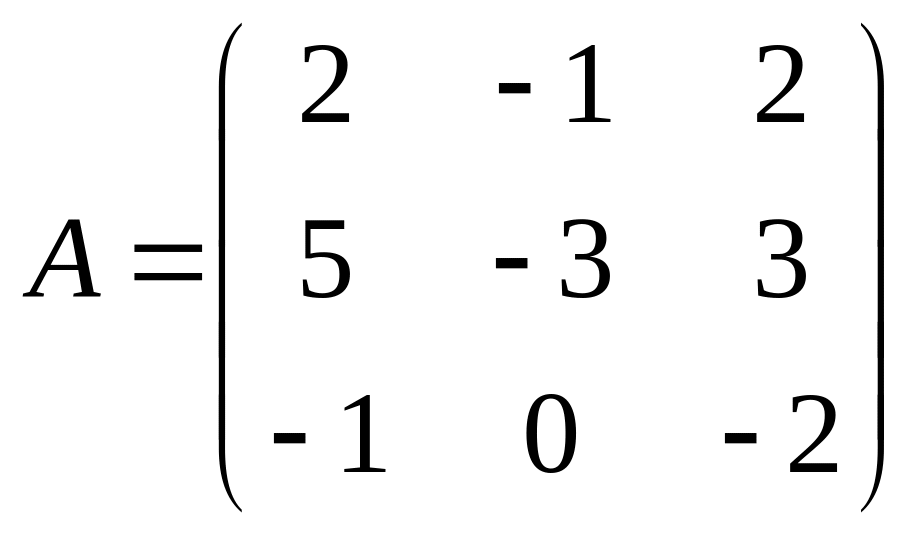 .
.
Решение. Собственные значения – решения характеристического уравнения:
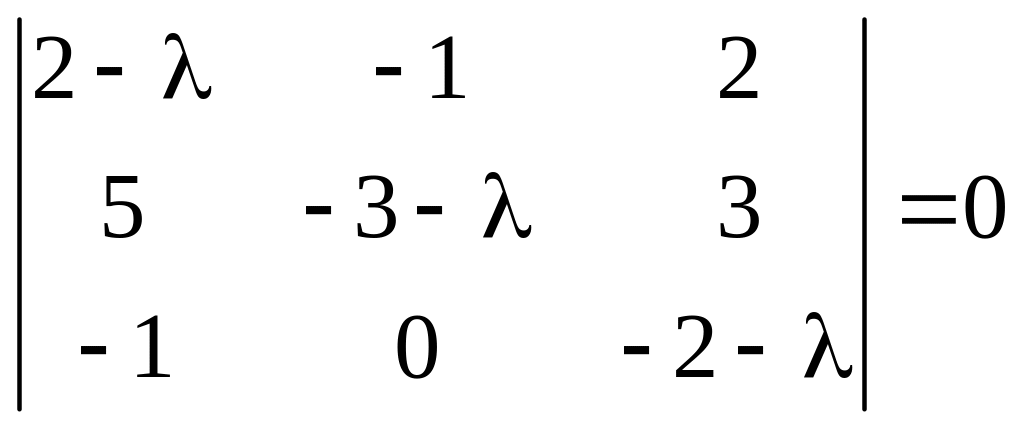
или
![]() ,
,
![]() являются кратными:
являются кратными:
![]() .
.
Найдем
собственный вектор, соответствующий
собственному значению
![]() .
Решением системы уравнений
.
Решением системы уравнений
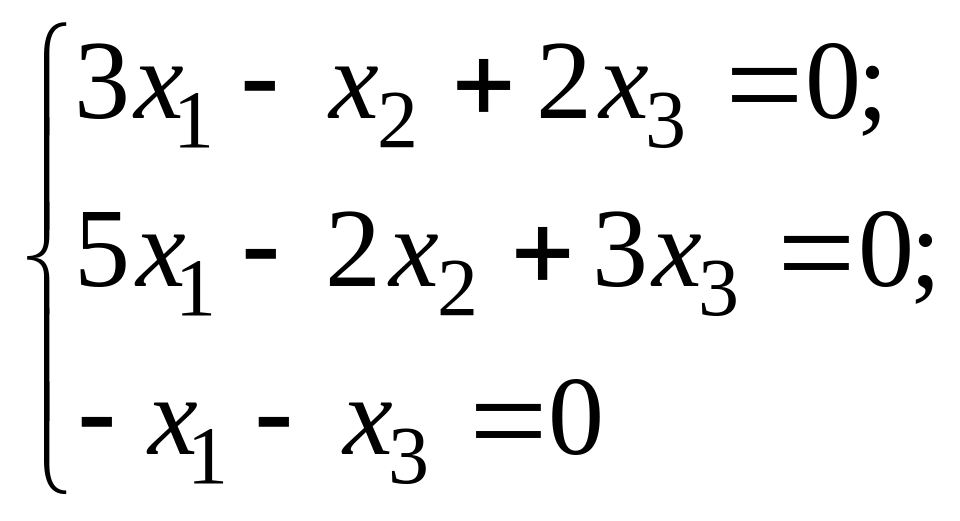
является
;
![]() ;
;
![]() ,
т.е. собственный вектор
,
т.е. собственный вектор
![]() .
При
имеем
.
При
имеем
![]() или
или
![]() .
.
Ответ. ; .
3)
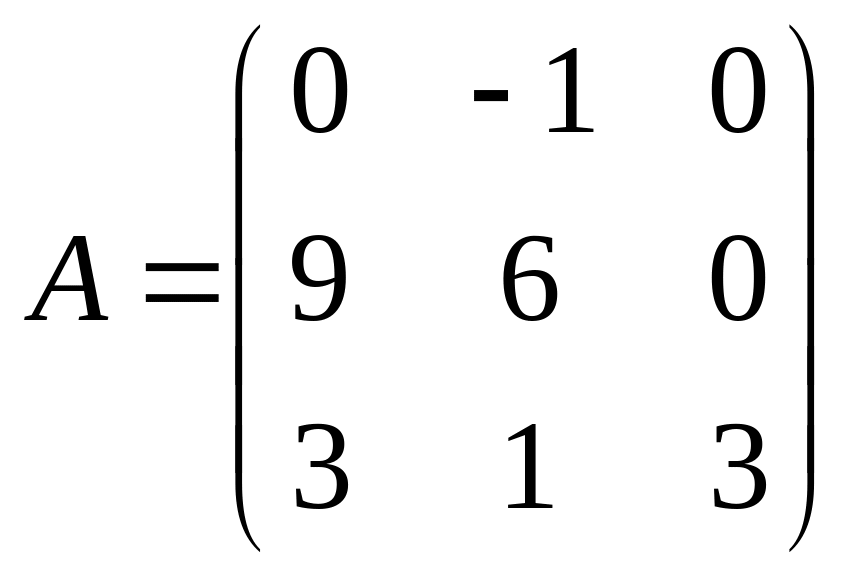 .
.
Решение. Характеристическое уравнение:
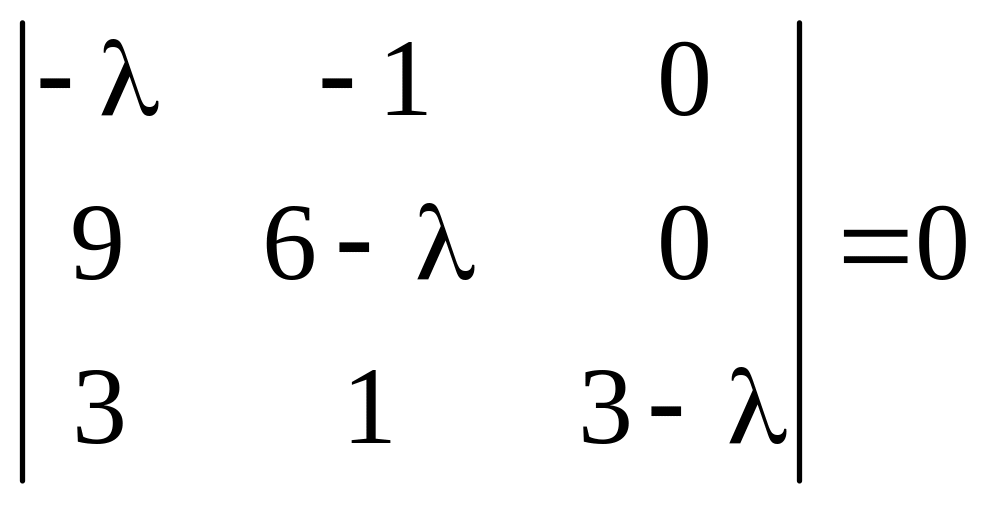 ,
,
разложением
по третьему столбцу получим:
![]() ,
,
![]() ;
тогда при
;
тогда при
![]()
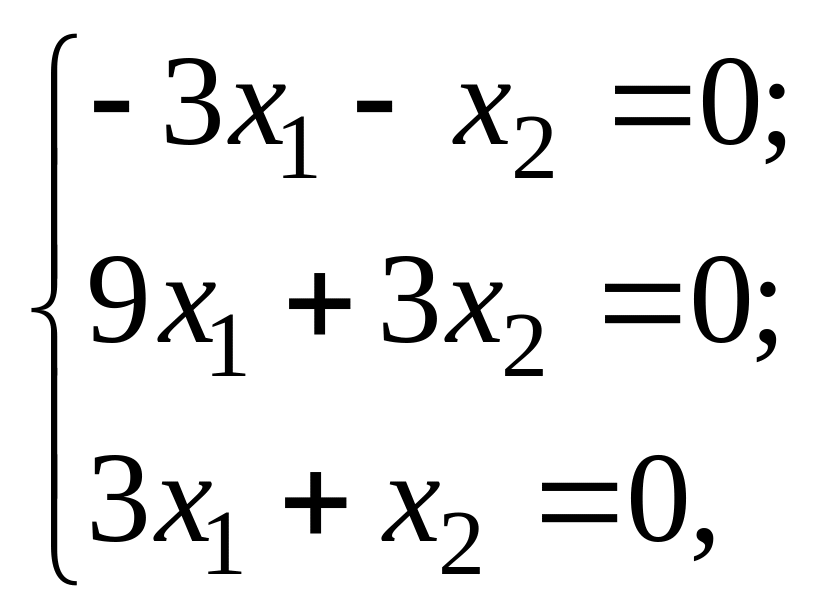 так как
–
так как
–
любое
число, обозначим
![]() .
.
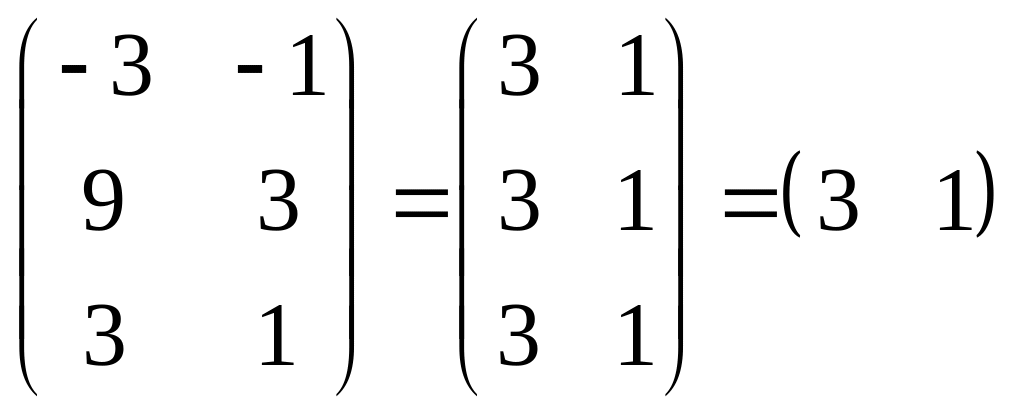 ,
,
если
,
тогда
![]() ,
собственный вектор:
,
собственный вектор:
![]() .
.
4)
 .
.
Решение. Характеристическое уравнение для этой матрицы имеет вид:
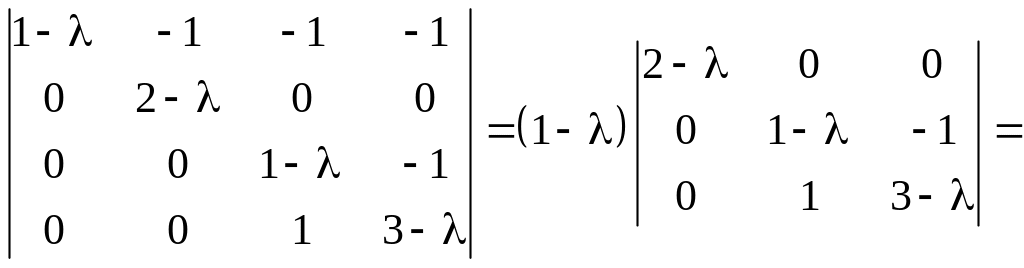
![]()
![]() .
.
Собственные
числа
![]() ;
;
![]() .
Для каждого
составим систему:
.
Для каждого
составим систему:
:
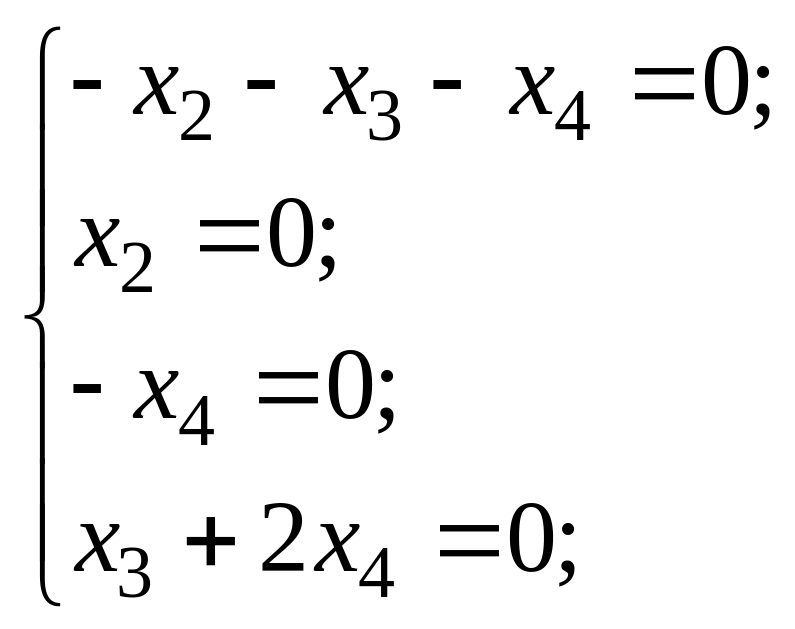
![]() :
:
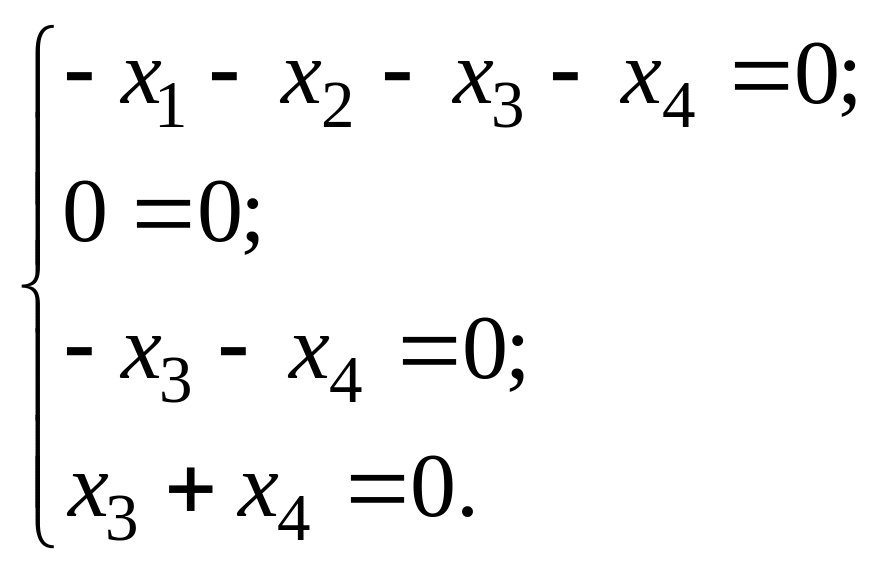
Решение
первой системы:
,
![]() ,
,
![]() ,
,
![]() ,
т.е. собственный вектор
,
т.е. собственный вектор
![]() .
Вторая система равносильна системе
.
Вторая система равносильна системе
![]() следовательно, ее решение:
;
;
;
следовательно, ее решение:
;
;
;
![]() ..
Собственный вектор –
..
Собственный вектор –
![]() .
При
,
.
При
,
![]() собственные векторы примут вид
собственные векторы примут вид
![]() ,
,
![]() .
.
Ответ.
;
![]() ;
;
![]() ,
.
,
.
Задачи для самостоятельного решения
Найти собственные числа и собственные векторы матриц.
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
Ответы:
1.
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
2.
,
![]() ;
;
![]() ,
,
![]() .
.
3.
![]() ,
,
![]() .
.
4.
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
5.
,
![]() ;
;
![]() ,
,
![]() .
.
6.
,
![]() .
.
7.
![]() ,
,
![]() .
.
8.
,
![]() ;
,
;
,
![]() ;
;
![]() ,
,
![]() .
.
9.
![]() ,
,
![]() ;
,
;
,
![]() .
.
10.
,
![]() .
.
Квадратичные формы
Определение. Квадратичной формой называется многочлен
![]() ,
,
где
![]() –
действительные постоянные,
–
действительные постоянные,
![]() – переменные.
– переменные.
Матрица называется матрицей квадратичной формы.
Пример. Записать матрицу квадратичной формы
![]() .
.
Решение. Диагональные элементы матрицы квадратичной формы равны коэффициентам при квадратах переменных, т.е. 1; 2; 5, а другие – половинам соответствующих коэффициентов квадратичной формы.
Перепишем ее в виде:
![]()
![]() ,
,
поэтому
 .
.
Так
как матрица
симметрическая, то всякая квадратичная
форма может быть приведена к каноническому
виду. Коэффициенты
![]() – собственные значения матрицы.
– собственные значения матрицы.
Определение. Каноническим видом квадратичной формы называется
![]() ,
,
т.е.
все
![]() при
при
![]() .
.
Квадратичная форма может быть приведена к каноническому виду произвольными неособенными линейными преобразованиями переменных, например, способом Лагранжа. Таких преобразований бесконечно много. Однако хотя коэффициенты и не совпадают, число положительных и отрицательных коэффициентов одно и то же. В системе координат с ортонормированным базисом преобразования должны быть ортогональными.
В
канонической квадратичной форме число
коэффициентов
![]() ,
отличных от нуля, равно рангу квадратичной
формы
,
отличных от нуля, равно рангу квадратичной
формы
![]() .
.
Примеры решения задач
Задача 1. Методом Лагранжа (выделения полных квадратов) привести к каноническому виду квадратичную форму
![]() .
.
Решение.
Первое преобразование:
![]() ,
,
![]() ,
,
![]() .
Тогда получим
.
Тогда получим
![]()
![]()
![]()
![]() .
.
Второе
преобразование:
![]() ;
;
![]() ;
;
![]()
и форма принимает канонический вид:
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() .
.
Ответ.
![]() .
.
Задача
2.
Найти ортогональное преобразование,
приводящее квадратичную форму
![]() к каноническому виду.
к каноническому виду.
Решение.
Диагональные элементы матрицы квадратичной
формы: 3, 2, 1, остальные элементы:
![]() ;
;
![]() ;
;
![]() .
Составим характеристическое уравнение
.
Составим характеристическое уравнение
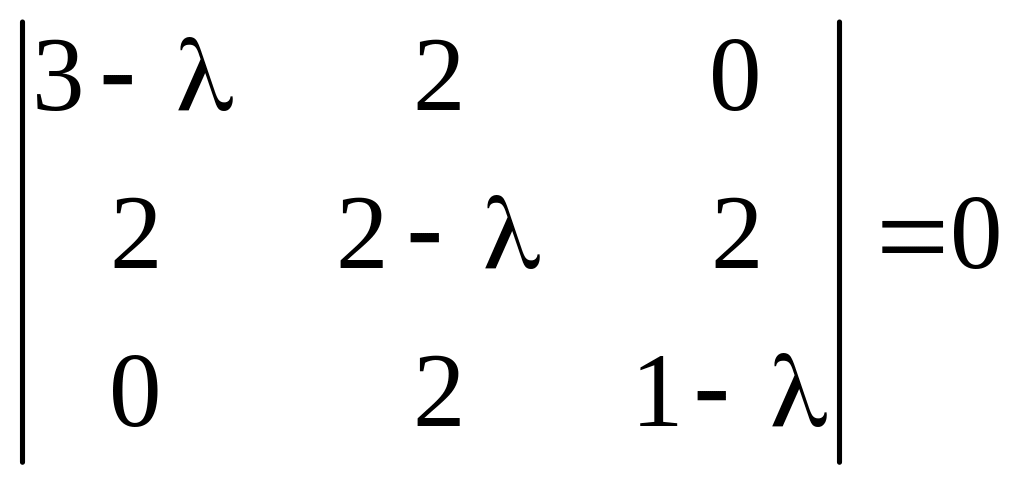 ;
;
![]() ;
;
или
![]() .
.
Корни:
;
;
![]() .
Найдем собственные векторы
.
Найдем собственные векторы
:
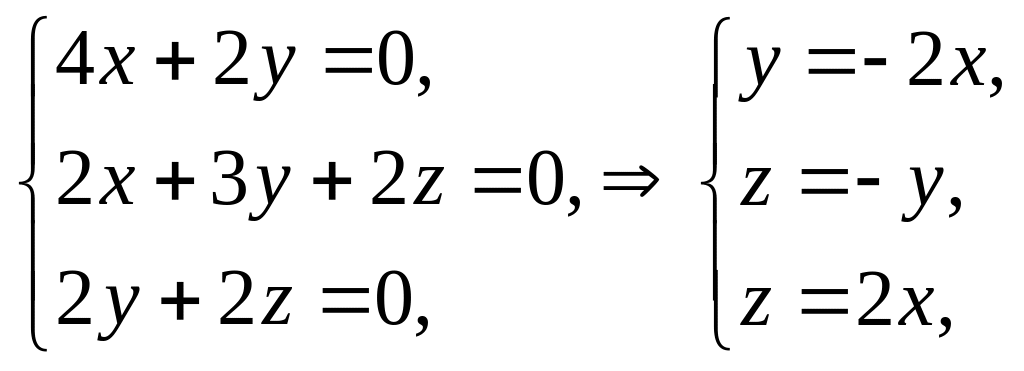
![]() при
при
![]() ;
;
:
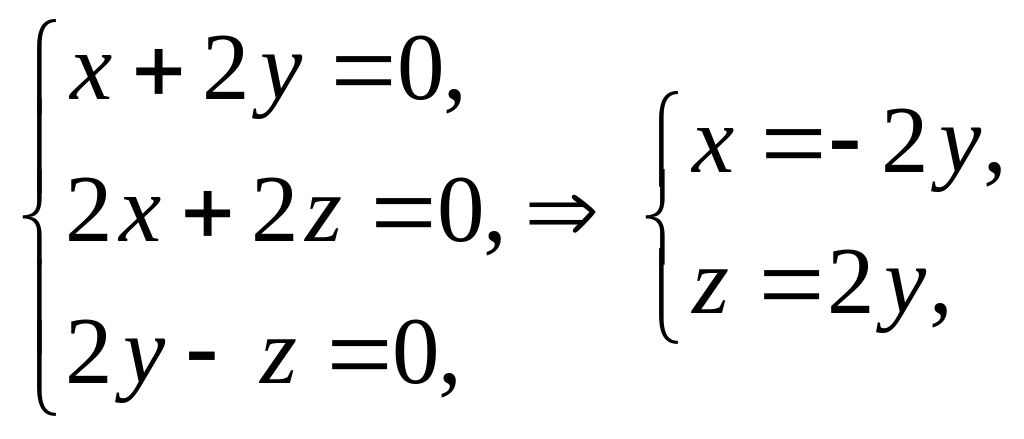
![]() или
или
![]() ;
;
:
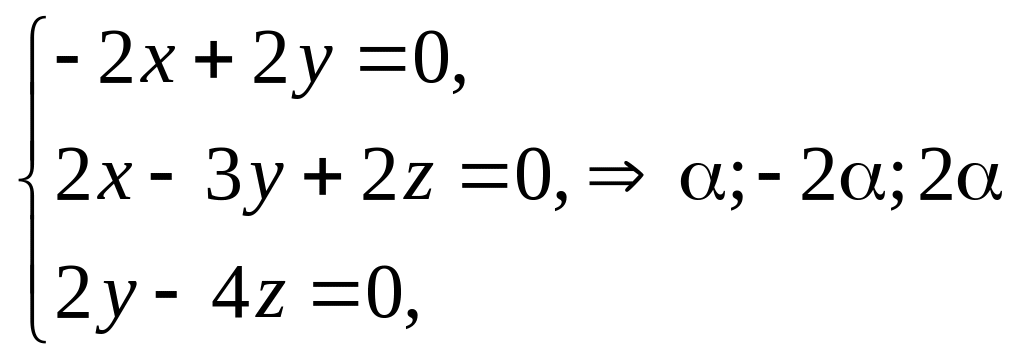
![]() ,
,
![]() .
.
Нормируем
систему векторов
![]() ,
,
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Следовательно,
![]() ,
,
![]() ,
,
![]() .
.
Формулы преобразования координат:
![]() ,
,
![]() ,
,
![]() .
.
Квадратичная
форма:
![]() .
.
Ответ.
![]() ,
,
,
,
, .
Задача 3. Привести к каноническому виду квадратичную форму:
![]() .
.
Решение. Характеристическое уравнение
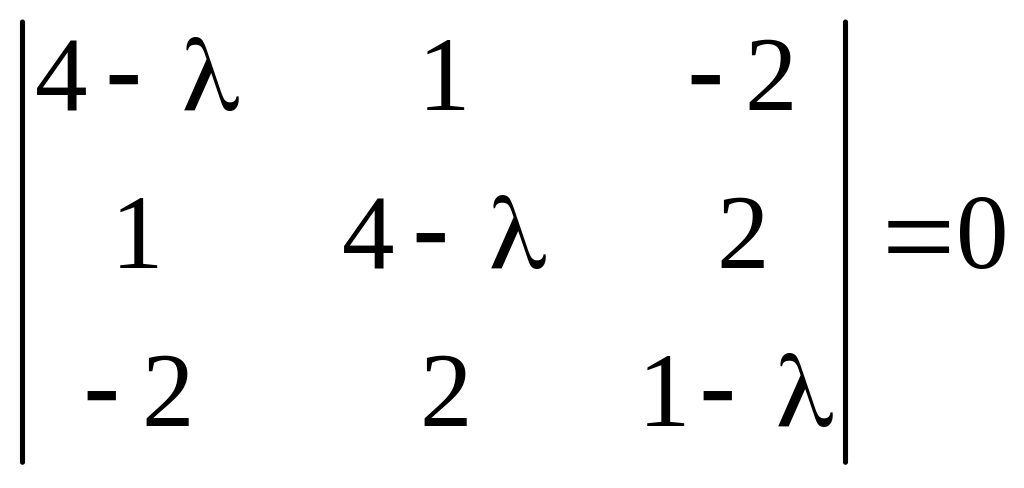 ,
,
![]() ,
,
![]() .
.
Решение
характеристического уравнения:
;
![]() .
Канонический вид:
.
Канонический вид:
![]() .
.
Найдем матрицу ортогонального преобразования
:
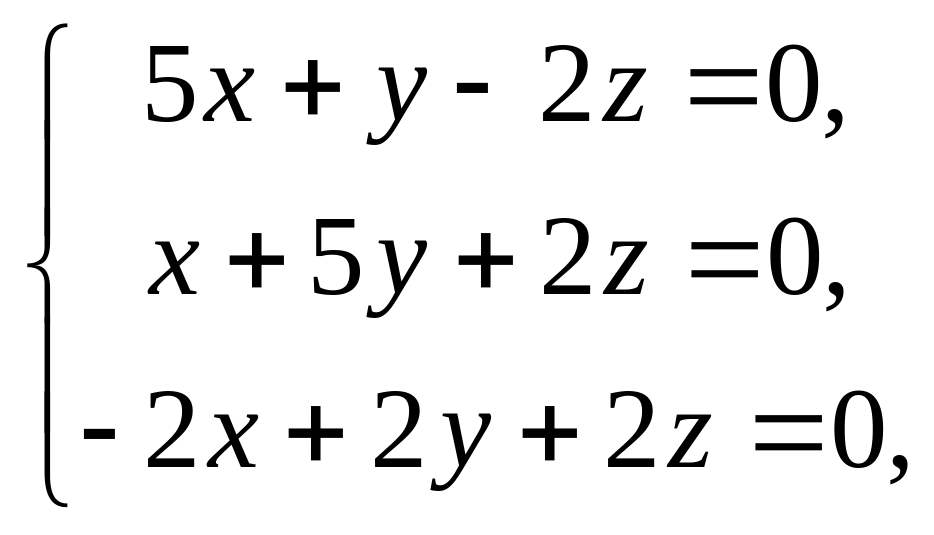
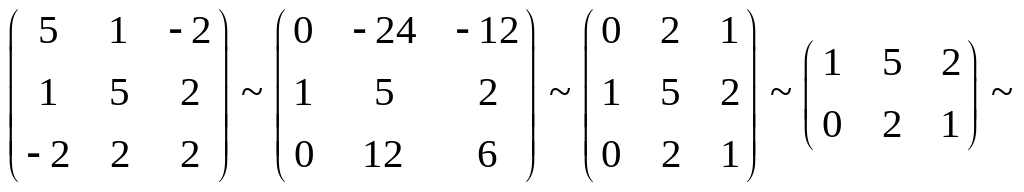
![]()
![]() ,
,
![]() ;
;
![]() ;
;
![]() :
:
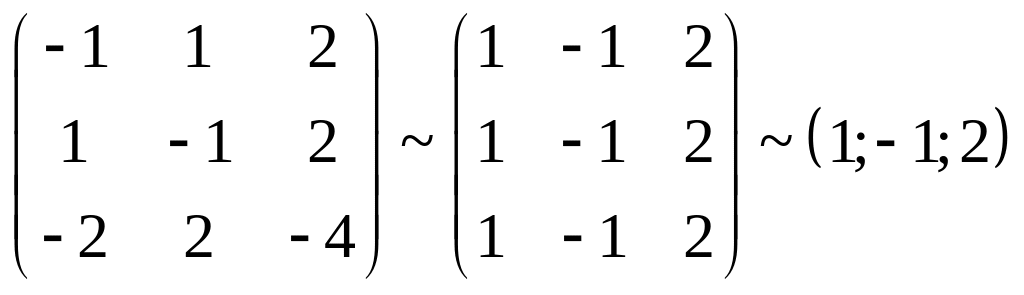 .
.
![]() ,
так как
,
так как
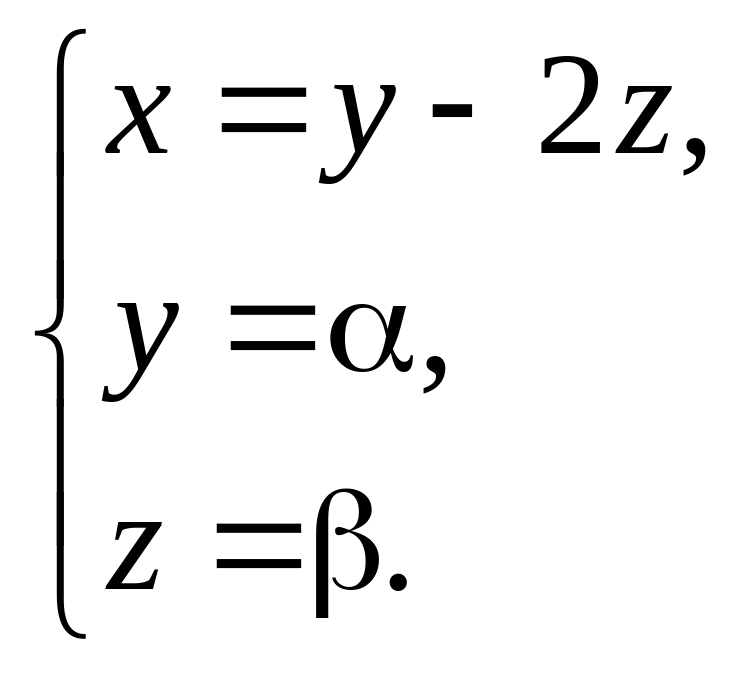
Корень
![]() кратности два, следовательно, этому
собственному значению соответствуют
два собственных вектора. Первый выбираем
произвольно. Пусть
кратности два, следовательно, этому
собственному значению соответствуют
два собственных вектора. Первый выбираем
произвольно. Пусть
![]() ;
;
![]() ,
,
![]() ,
тогда
,
тогда
![]() .
.
Второй
выбираем так, чтобы
![]() ,
т.е.
,
т.е.
![]() .
.
![]() ,
,
,
,
– любое;
![]() ,
,
![]() ,
,
![]() .
.
Матрица преобразования:
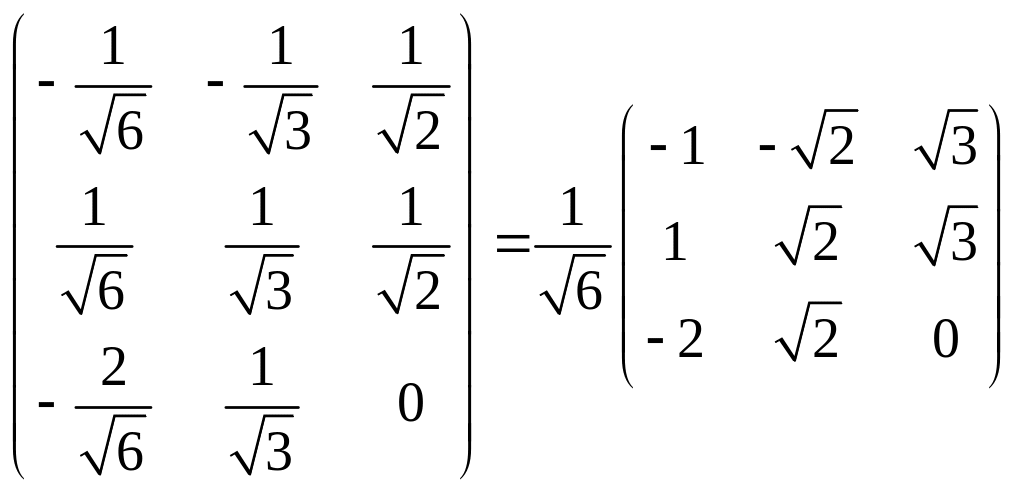 .
.
Формулы преобразования координат:
![]() ;
;
![]() ;
;
![]() .
.
Подставляем в исходную матрицу квадратичную форму:
![]()
![]()
![]()
![]()
![]() .
.
Ответ.
![]() .
.
Задачи для самостоятельного решения
Методом Лагранжа привести к каноническому виду квадратичные формы:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
Ответ: 1)
![]() ;
;
2)
![]() ;
;
3) .
Найти ортогональное преобразование, приводящее следующие формы к каноническому виду, и написать этот канонический вид:
4. ![]() .
.
Ответ.
![]() ,
,
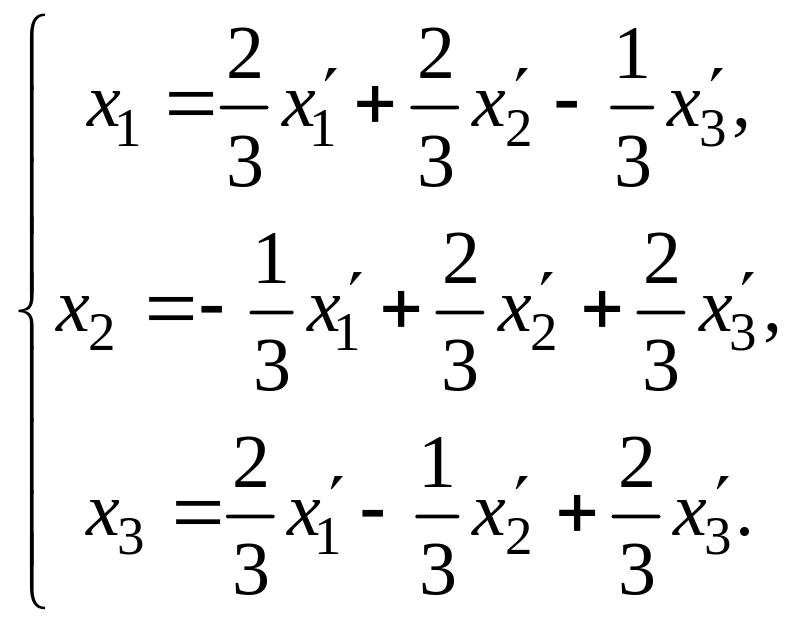
5.
![]() .
.
Ответ.
![]() ,
,
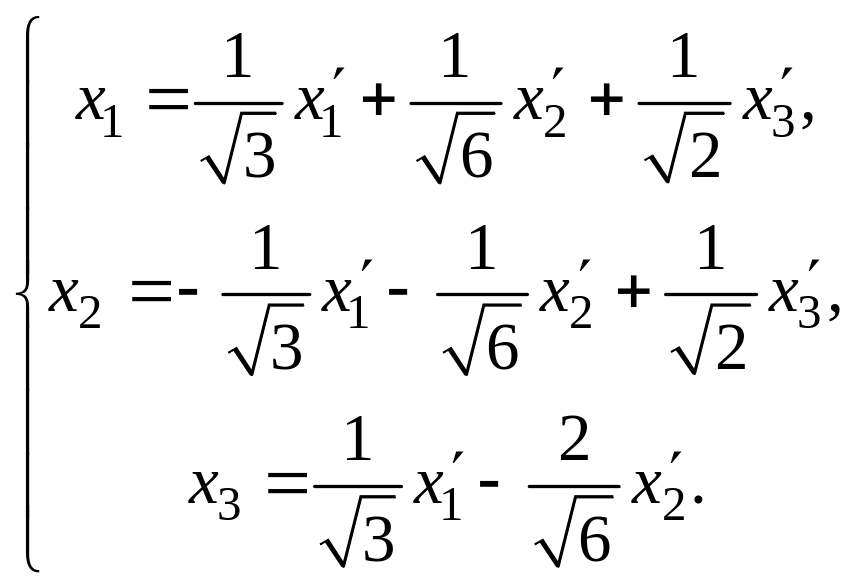
6.
![]() .
.
Ответ.
![]() ,
,
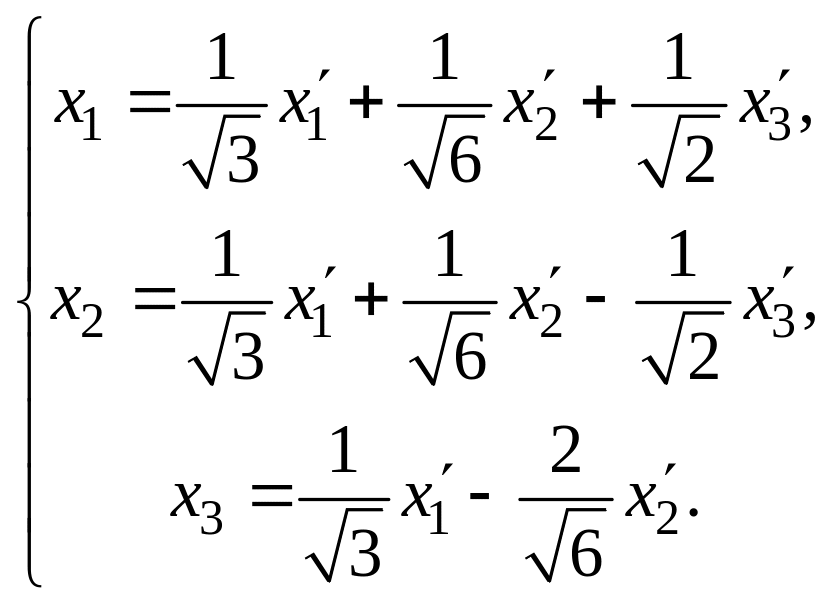
7.
![]() .
.
Ответ.
![]() ,
,
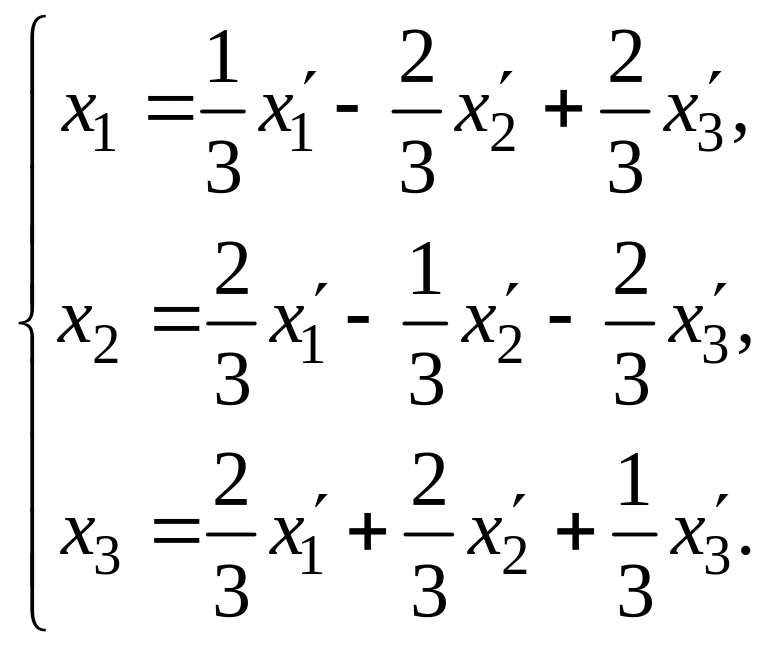

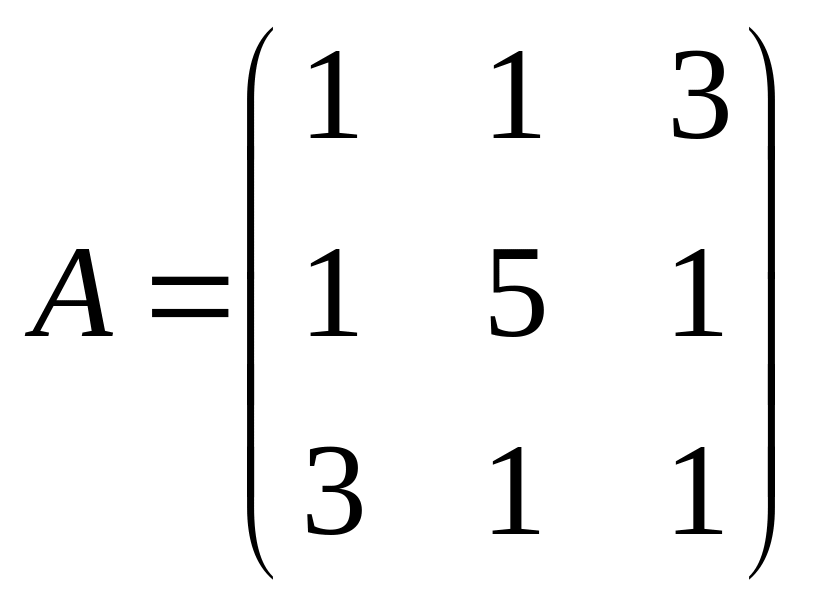 .
.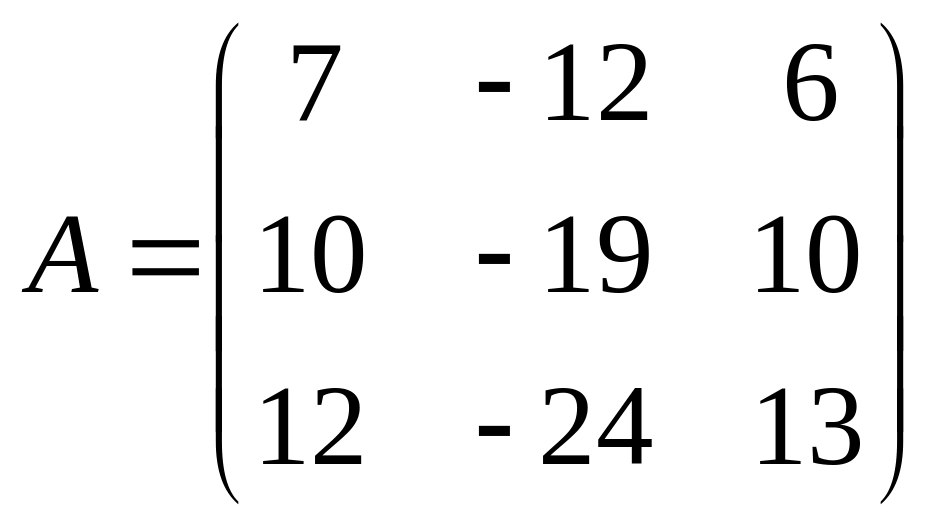 .
.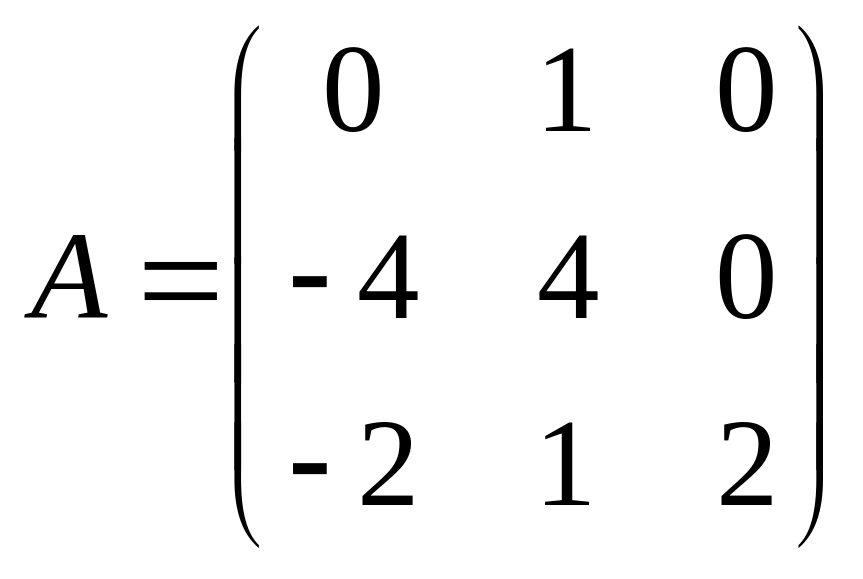 .
.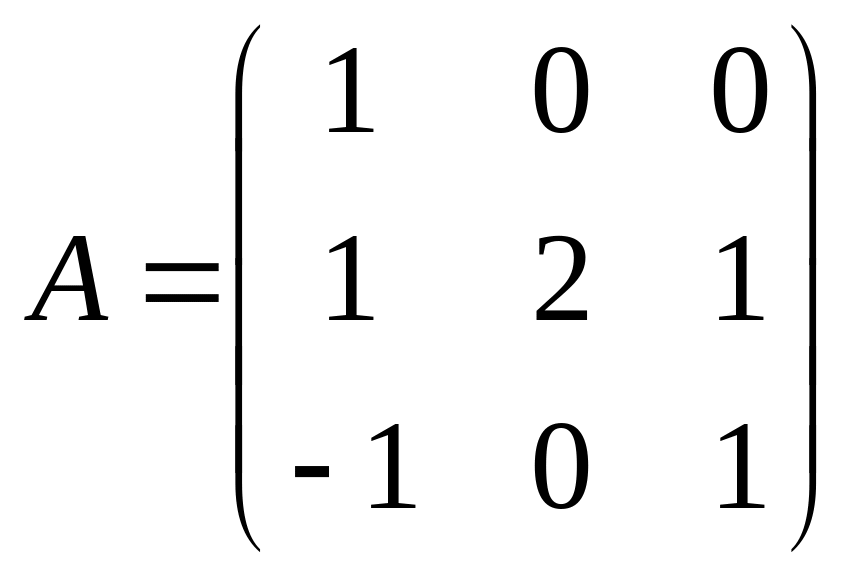 .
.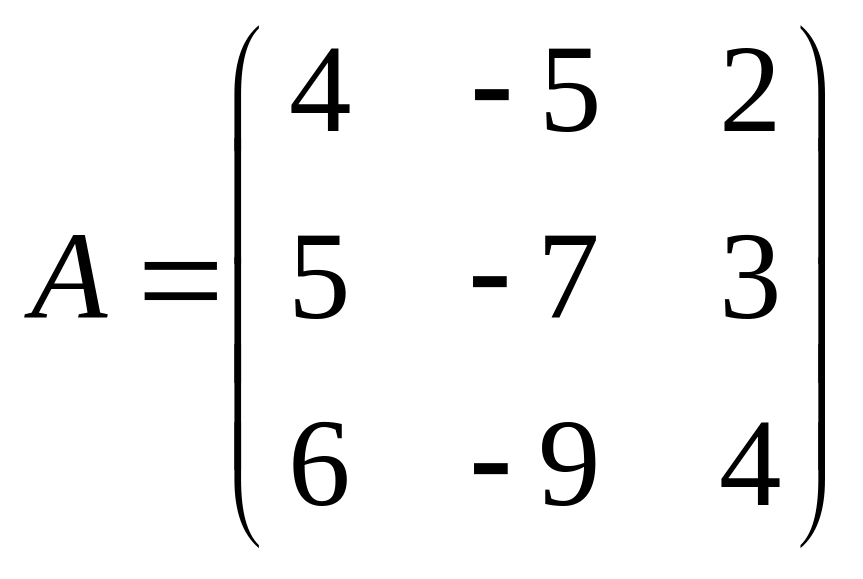 .
. .
.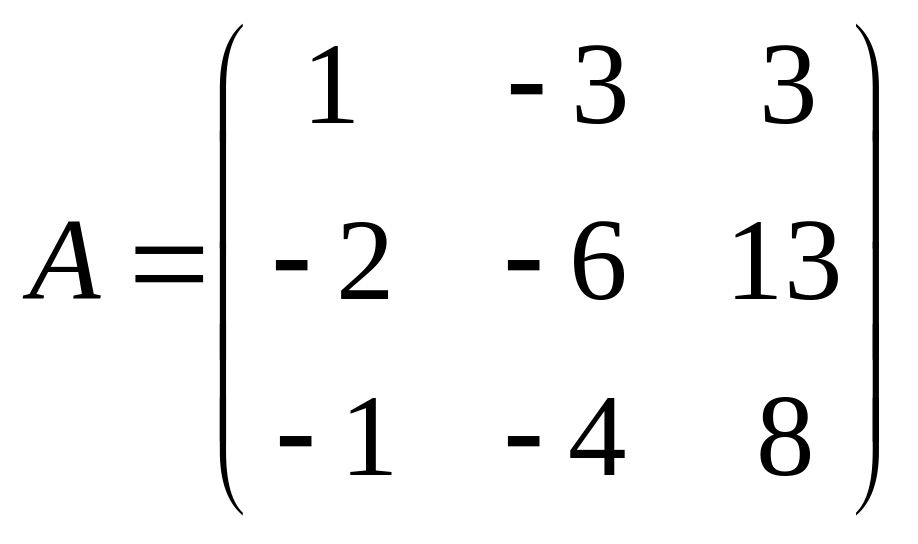 .
. .
.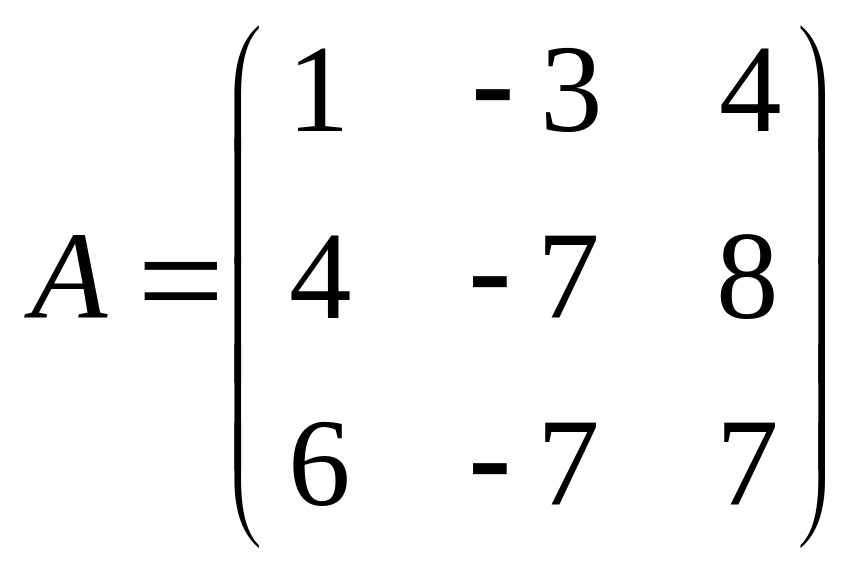 .
.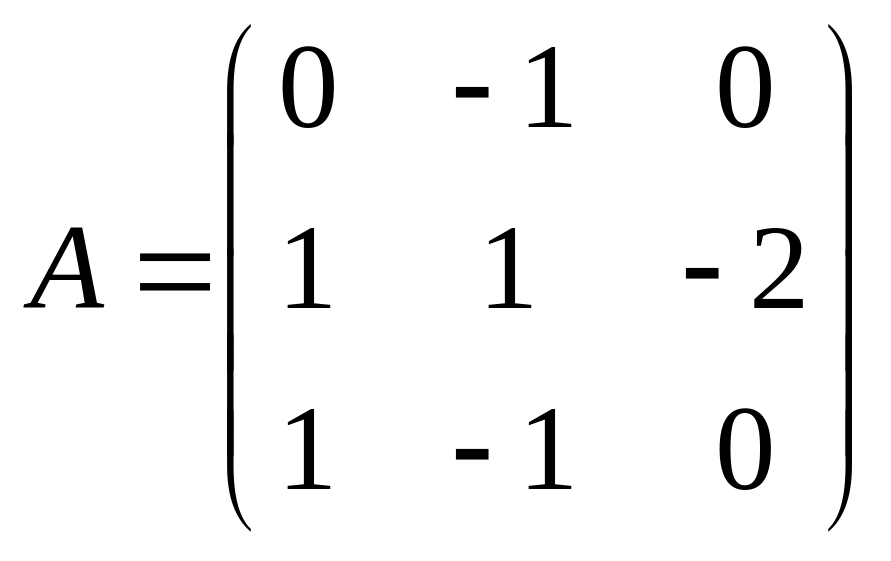 .
.