
- •Определители. Свойства определителей Основные теоретические сведения
- •Основные свойства определителей
- •Приведение определителя к треугольному виду
- •Решение систем уравнений с помощью определителей (по формулам Крамера) Основные теоретические сведения
- •Матрицы. Операции над матрицами Основные теоретические сведения
- •Операции над матрицами
- •Многочлены от матриц
- •Обратная матрица
- •Решение систем алгебраических уравнений методом гаусса Основные теоретические сведения
- •Метод Гаусса. Схема с выбором главного элемента
- •Собственные векторы и собственные значения линейного преобразования Основные теоретические сведения
- •Квадратичные формы
- •Кривые и поверхности второго порядка Основные теоретические сведения
- •Список литературы
- •Оглавление
Матрицы. Операции над матрицами Основные теоретические сведения
Определение 1. Матрица – прямоугольная таблица чисел, имеющая строк и столбцов. Обозначения:
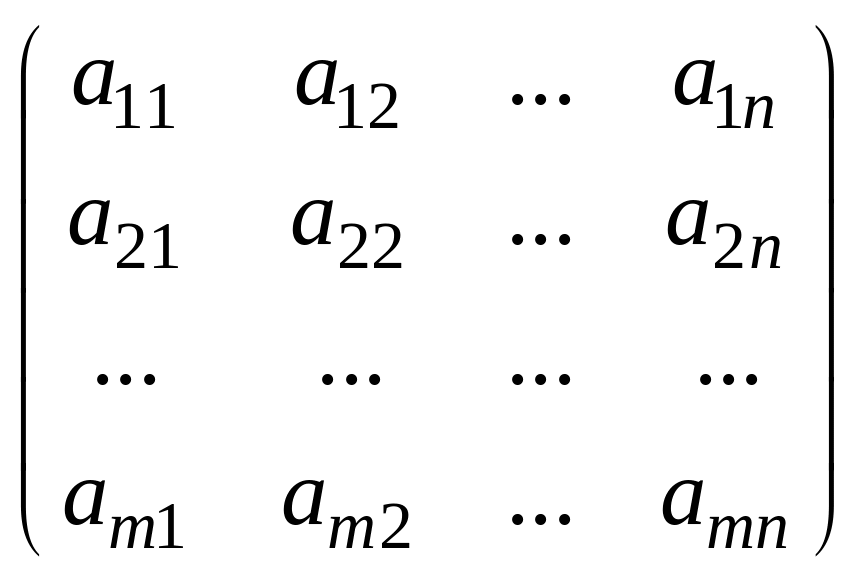 или
или
 или
или
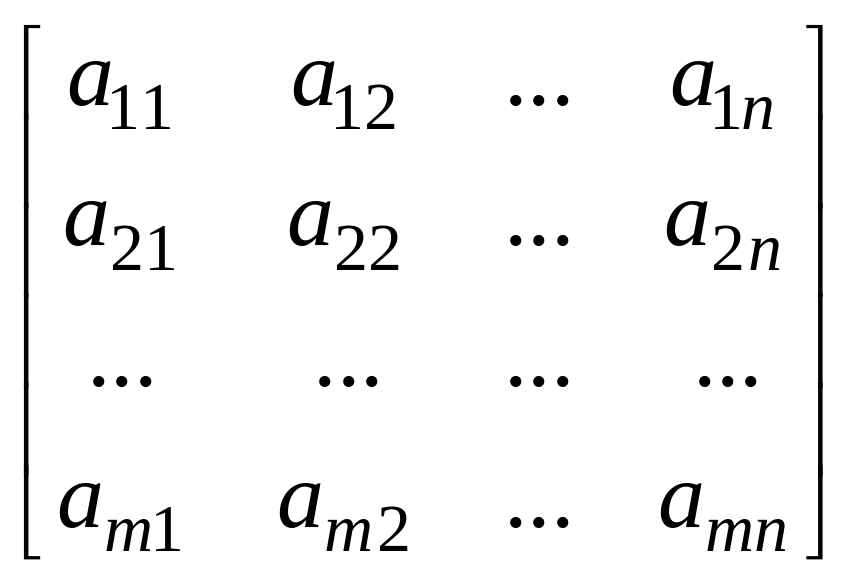 ,
,
где
,
![]() ,
,
![]() – элементы матрицы.
– элементы матрицы.
Матрицы
обычно обозначают заглавными буквами
латинского алфавита:
![]() ,
где
,
;
,
где
,
;
![]()
Матрица,
состоящая из одной строки, т.е.
![]() ,
называется матрицей-строкой,
а из одного столбца, т.е.
,
называется матрицей-строкой,
а из одного столбца, т.е.
![]() ,
матрицей-столбцом.
,
матрицей-столбцом.
Определение
2.
Матрицы называются равными,
если имеют одинаковую
размерность и их соответствующие
элементы равны, т.е.
![]() .
.
Определение
3.
Если
,
матрицу называют квадратной. В квадратной
матрице элементы
![]() составляют главную диагональ, а
составляют главную диагональ, а
![]() побочную.
побочную.
Нулевая матрица – матрица, все элементы которой равны нулю:
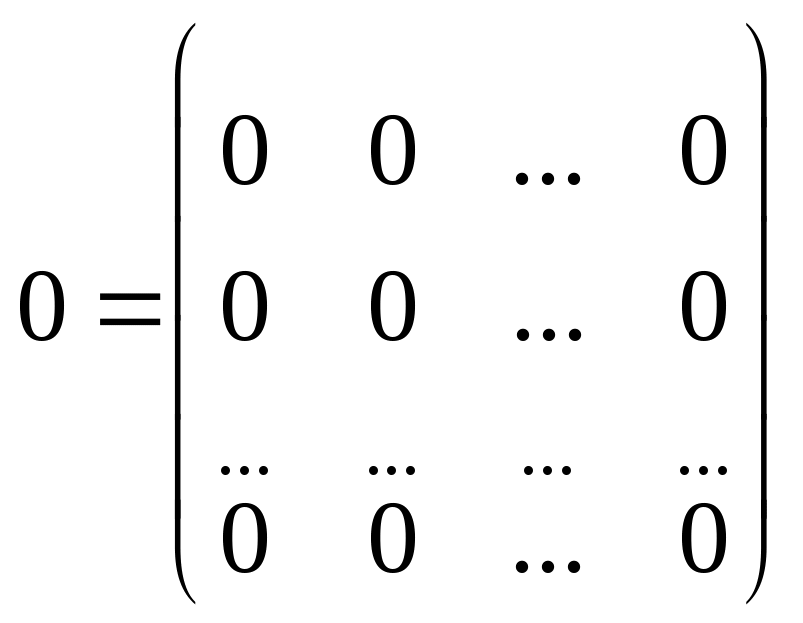 .
.
Диагональная матрица – квадратная матрица, у которой все элементы, кроме стоящих на главной диагонали равны нулю.
Единичная матрица – диагональная матрица, все элементы главной диагонали равны единице.
Треугольная матрица – квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.
Трапециевидная (треугольно-ступенчатая) матрица имеет вид:
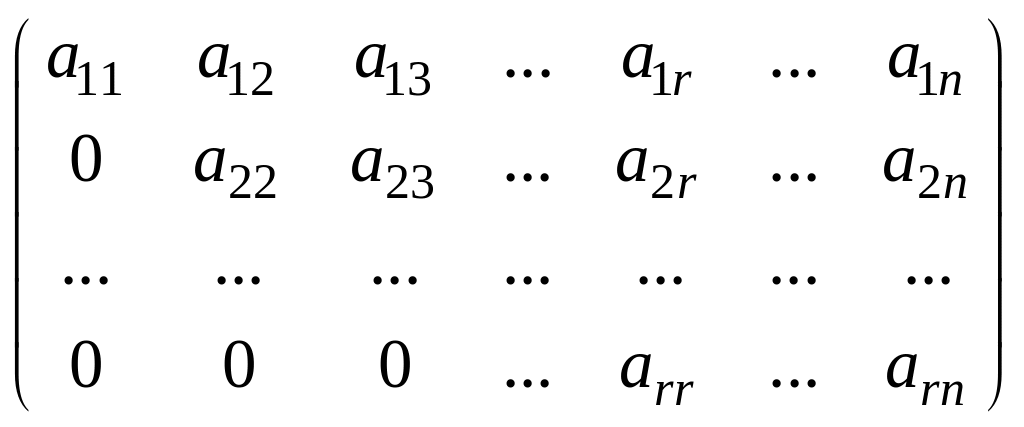 .
.
Противоположная
матрица (не обратная !)
![]()
Операции над матрицами
Сложение
(только для матриц одинаковой размерности):
если
![]() и
и
![]() ,
то
,
то
![]() ,
где
,
где
![]() .
.
Примечание. Аналогично определяется сумма конечного числа матриц одинаковой размерности.
Умножение
матрицы на число (или числа на матрицу):
если
,
– число, то
![]() ,
где
,
где
![]() .
.
Умножение
матриц.
Матрицу
![]() будем называть согласованной с матрицей
будем называть согласованной с матрицей
![]() ,
если число столбцов матрицы
равно числу строк матрицы
(или
длина строки матрицы
равна высоте столбца матрицы
).
Из согласованности
с
не следует согласованность
с
.
Произведение
,
если число столбцов матрицы
равно числу строк матрицы
(или
длина строки матрицы
равна высоте столбца матрицы
).
Из согласованности
с
не следует согласованность
с
.
Произведение
![]() возможно только в случае согласованности
матрицы
с матрицей
:
возможно только в случае согласованности
матрицы
с матрицей
:
![]() ,
где
,
где
![]() .
.
Замечание.
Если матрицу
можно умножить на
,
т.е. существует произведение
![]() ,
то это не значит, что существует
произведение
,
то это не значит, что существует
произведение
![]() (в
общем случае
(в
общем случае
![]() ).
).
Если
![]() ,
то матрицы называются коммутативными
(перестановочными, коммутирующими).
,
то матрицы называются коммутативными
(перестановочными, коммутирующими).
Произведение двух ненулевых матриц может быть нулевой матрицей (для произведения чисел этого быть не может), например,
![]() .
.
Многочлены от матриц
Целой
положительной степенью
![]()
![]() квадратной матрицы
называется
квадратной матрицы
называется
![]() .
.
Пусть
дан многочлен
![]() Если
Если
![]() есть нулевая матрица, то
называется корнем
есть нулевая матрица, то
называется корнем
![]() .
.
Обратная матрица
Матрица
называется обратной к матрице
,
если
![]() где
где
![]() единичная матрица.
единичная матрица.
Минор
матрицы – определитель матрицы,
полученной из элементов, стоящих на
пересечении произвольно выбранных
![]() строк и
столбцов. Обозначение: М.
Минор
называется дополнительным к минору М
и состоит из оставшихся после вычеркивания
-й
строки и
-го
столбца элементов. Это понятие применяется
к квадратной матрице.
строк и
столбцов. Обозначение: М.
Минор
называется дополнительным к минору М
и состоит из оставшихся после вычеркивания
-й
строки и
-го
столбца элементов. Это понятие применяется
к квадратной матрице.
Алгебраическое дополнение .
Невырожденной
называется
квадратная матрица
,
если
![]()
Теорема. Для того чтобы существовала обратная матрица к квадратной матрице , необходимо и достаточно, чтобы матрица была невырожденной.
Если
 ,
,
то обратная матрица имеет вид
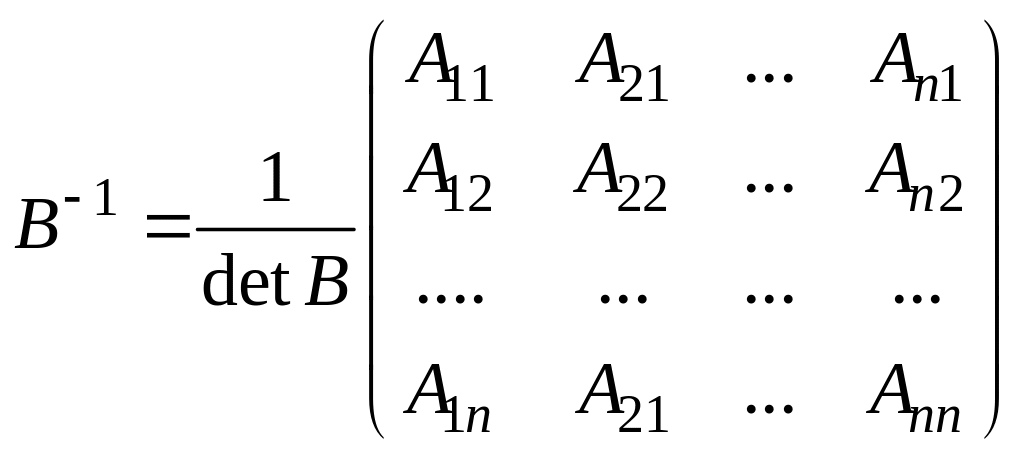 ,
,
где
![]() алгебраические дополнения элементов
алгебраические дополнения элементов
![]() .
.
Обратную
матрицу можно найти и с помощью
элементарных преобразований:
![]()
Определение
4.
Рангом матрицы
называется наибольший из порядков
миноров матрицы, отличных от нуля.
Обозначение:
![]() ,
,
![]() .
.
Примеры решения задач
Задача
1.
Умножить матрицу
![]() на число
на число
![]() .
.
Решение.
![]() .
.
Задача
2.
Дано:
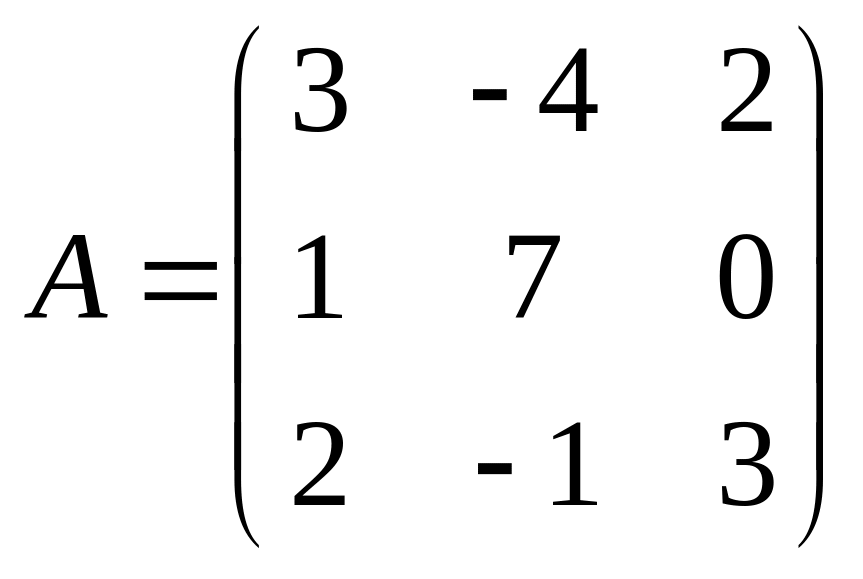 ,
,
![]() .
Найти
.
Найти
![]() и
и
![]() .
.
Решение.
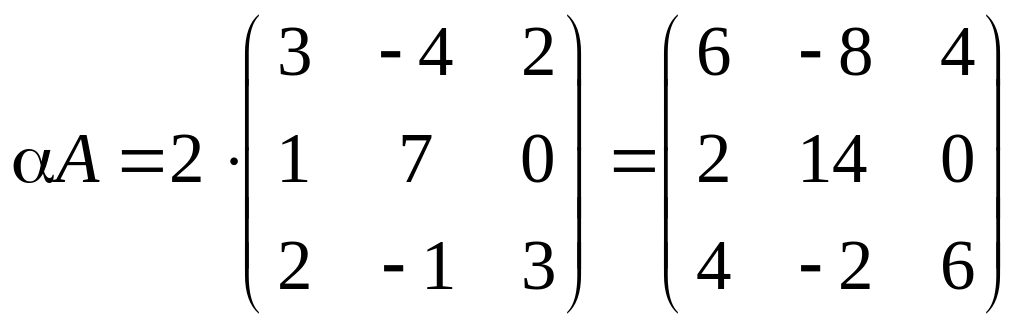 ,
,
каждый элемент умножили на число 2. При умножении определителя на число умножаем на это число какой-либо ряд:

и т.д. В первом случае умножим на 2 первую строку, во втором – второй столбец, в третьем – третий столбец.
Задача
3.
Найти произведения
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
если они существуют:
,
если они существуют:
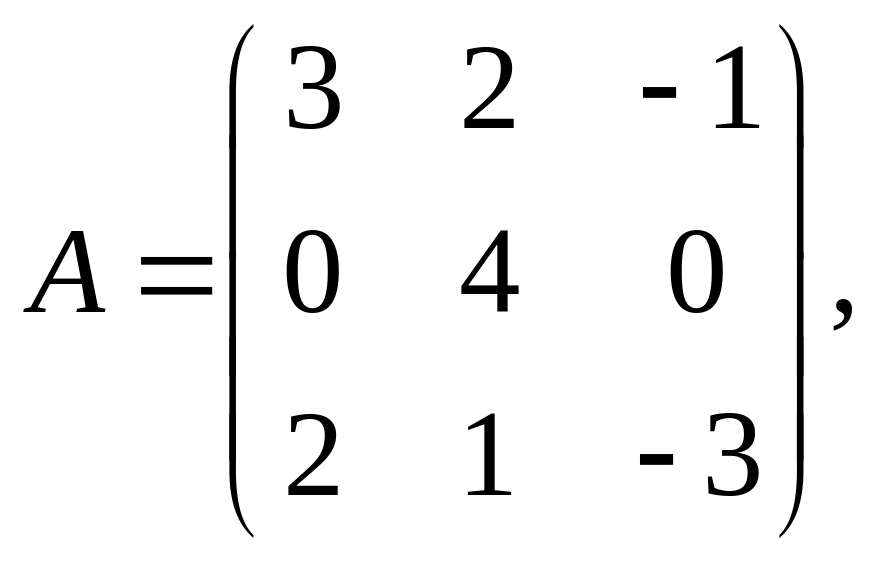
![]()
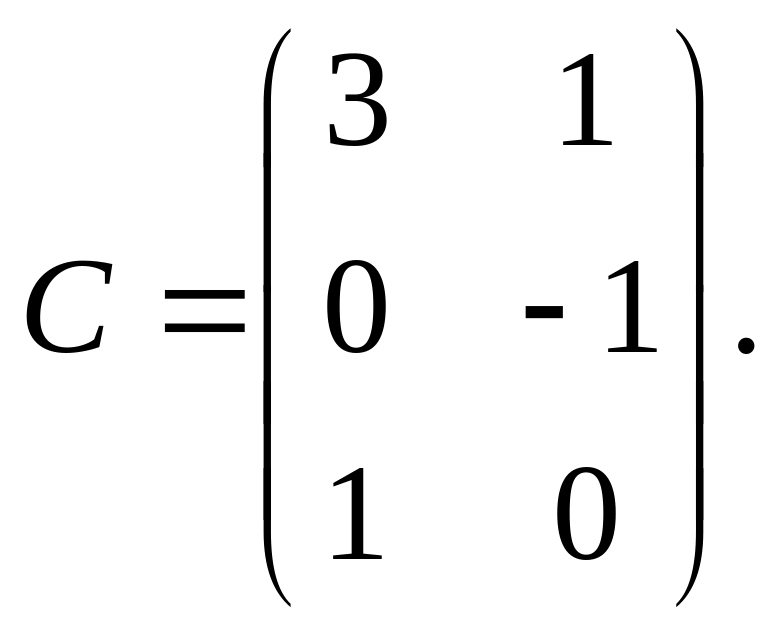
Решение.
Проверим согласованность матриц
![]() ,
,
![]() ,
,
![]() .
.
Для
:
![]() ,
длина строк матрицы
не равна высоте столбца
матрицы
,
следовательно, матрицы перемножать
нельзя.
,
длина строк матрицы
не равна высоте столбца
матрицы
,
следовательно, матрицы перемножать
нельзя.
Для
:
![]() матрицы согласованы, получим матрицу
размерности
матрицы согласованы, получим матрицу
размерности
![]() :
:
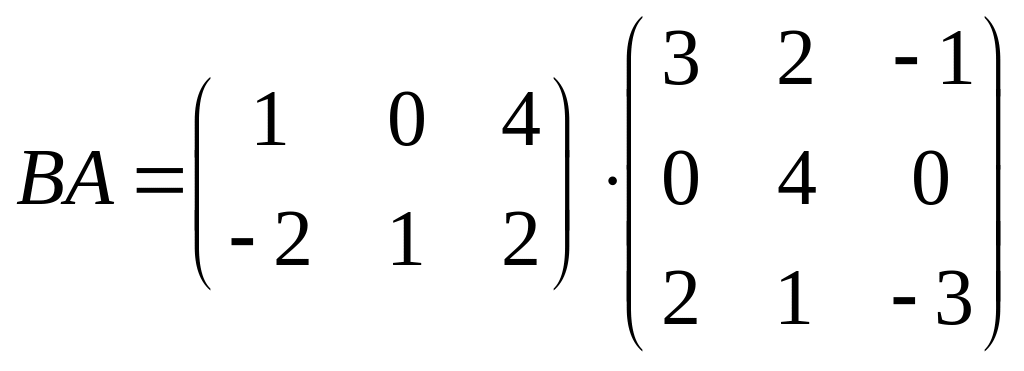
![]()
![]() .
.
Для
– матрицы согласованы, в результате
получим матрицу размерностью
![]() :
:
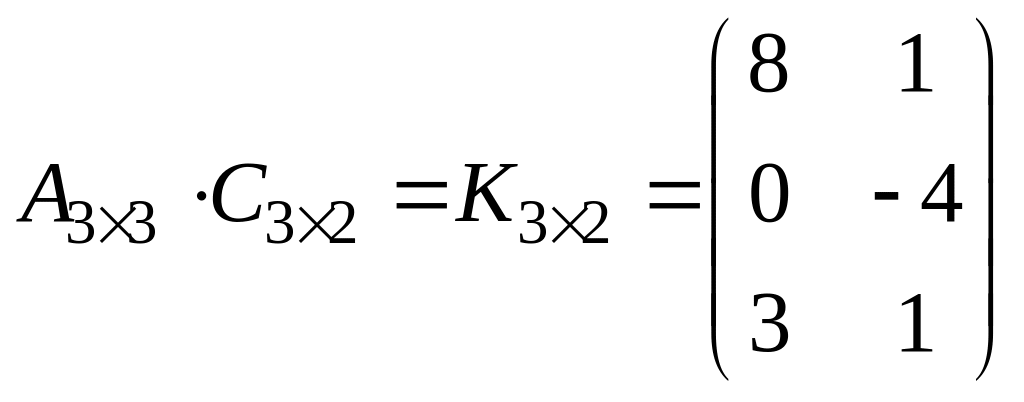 .
.
Для
:
![]() – произведение не существует.
– произведение не существует.
Для
матрицы
согласованы
![]() :
:
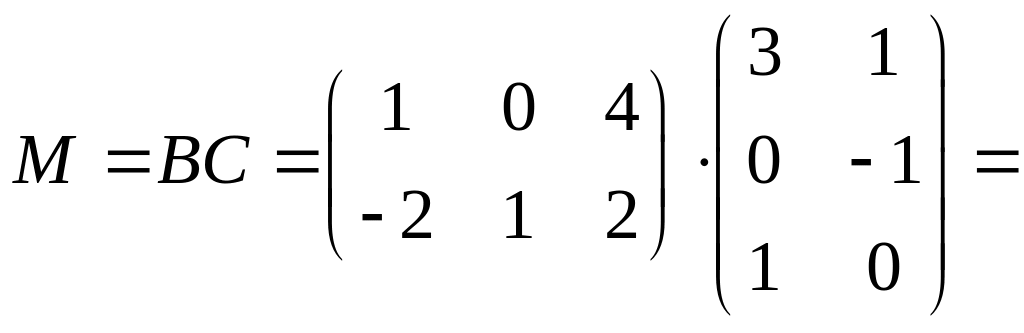
![]() .
.
Заметим,
что элементы матрицы произведения
получаются при перемножении
-й
строки матрицы
на
-й
столбец матрицы
![]() :
:
![]() ,
,
 .
.
Для : квадратичная матрица всегда согласована с квадратичной матрицей той же размерности
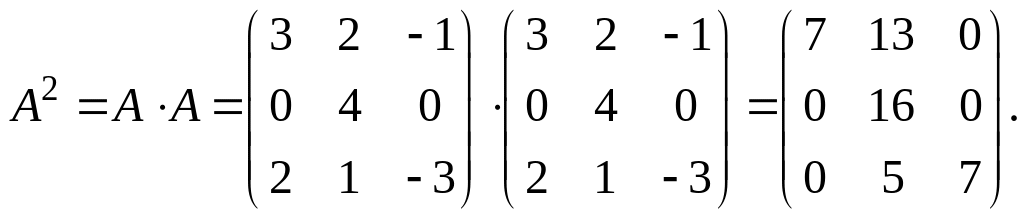
Задача
4.
Дано:
![]() ,
,
![]() .
Найти
.
.
Найти
.
Решение.
![]() ,
,
![]() .
.
Таким образом, – матрицы коммутативны.
Задача
5.
Показать, что
![]() является корнем многочлена
является корнем многочлена
![]() .
.
Решение.
![]()
![]() ,
,
так как получили нулевую матрицу, матрица является корнем многочлена .
Задача
6.
Найти определитель произведения матрицы
А=![]() на транспонированную
на транспонированную![]() .
.
Решение.
Пусть
![]() ,
тогда
,
тогда
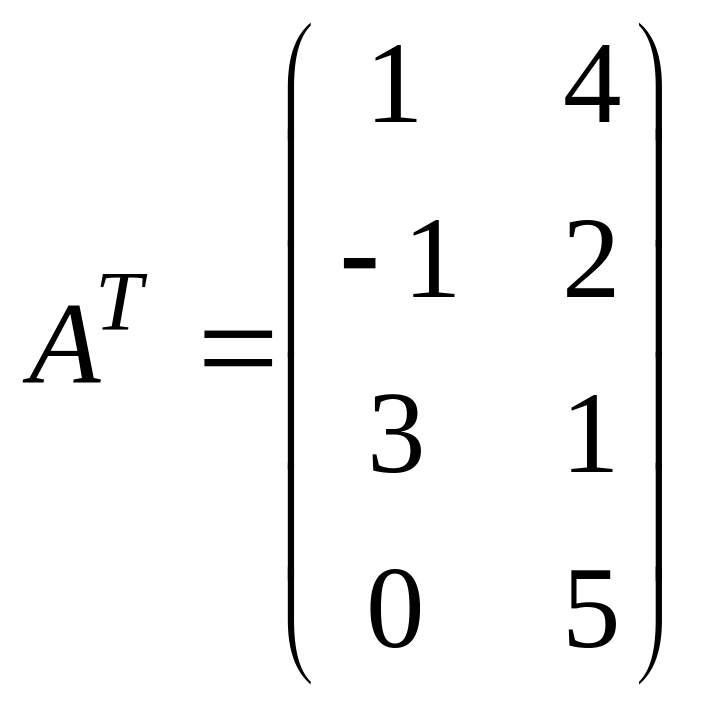 и
и

![]() ,
,
![]()
Задача 7. Найти обратную матрицу, если она существует:
а)
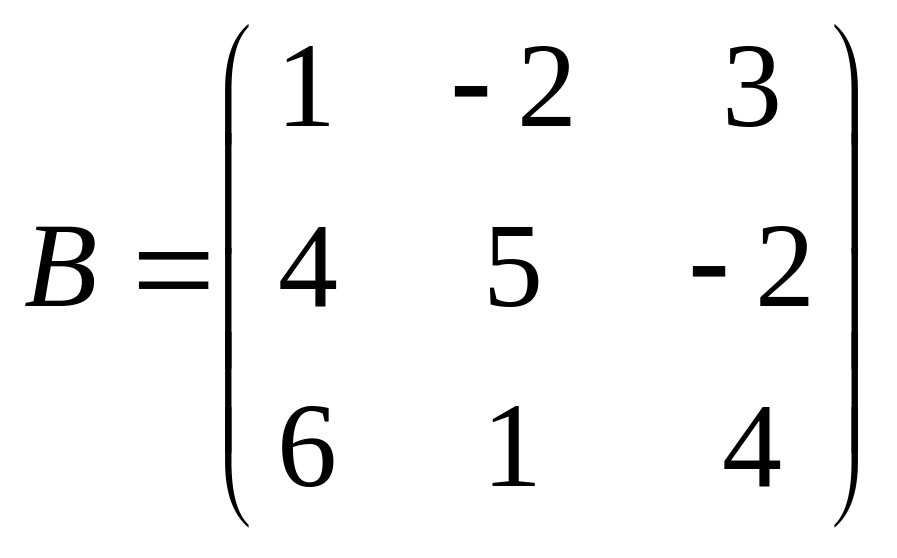 ,
б)
,
б)
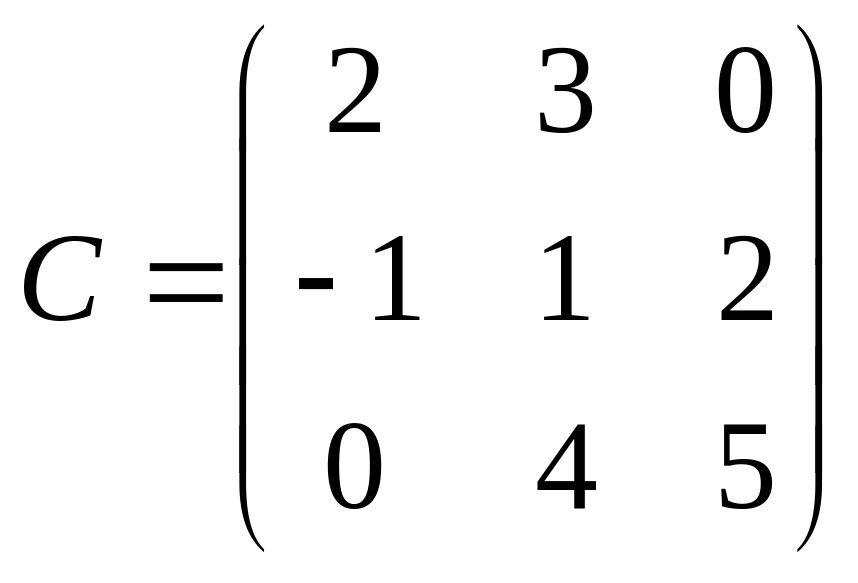 .
.
Решение.
а)
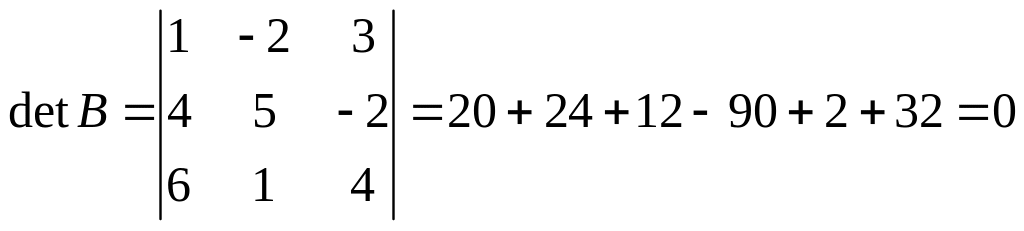 ,
матрица
вырожденная, так как
,
матрица
вырожденная, так как
![]() и обратной матрицы не имеет;
и обратной матрицы не имеет;
б)
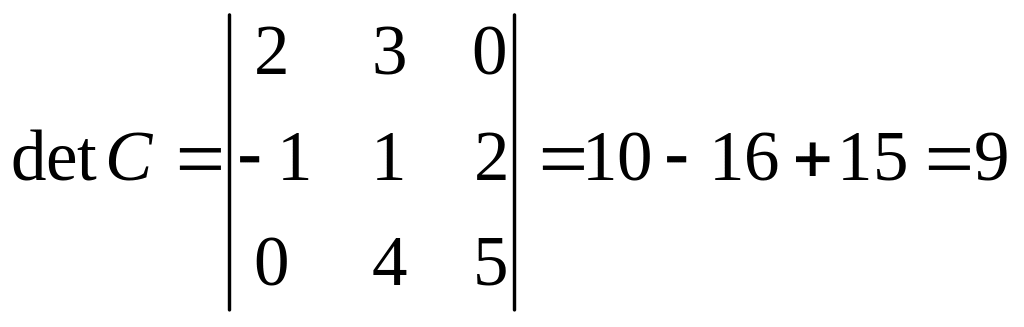 ,
,
![]() Найдем алгебраические дополнения
Найдем алгебраические дополнения
![]() ,
,
![]() ,
,
![]() ;
;
алгебраическое
дополнение первой строки запишем в
первый столбец обратной матрицы:
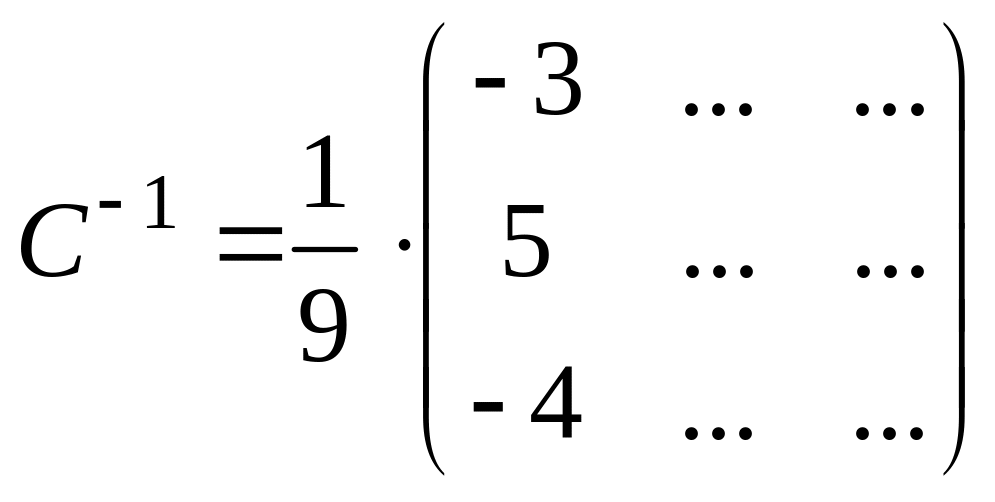 .
.
Ищем алгебраическое дополнение второй строки:
![]() ,
,
![]() ,
,
![]() ;
;
 .
.
Ищем алгебраическое дополнение третьей строки:
![]() ,
,
![]() ,
,
![]() ;
;
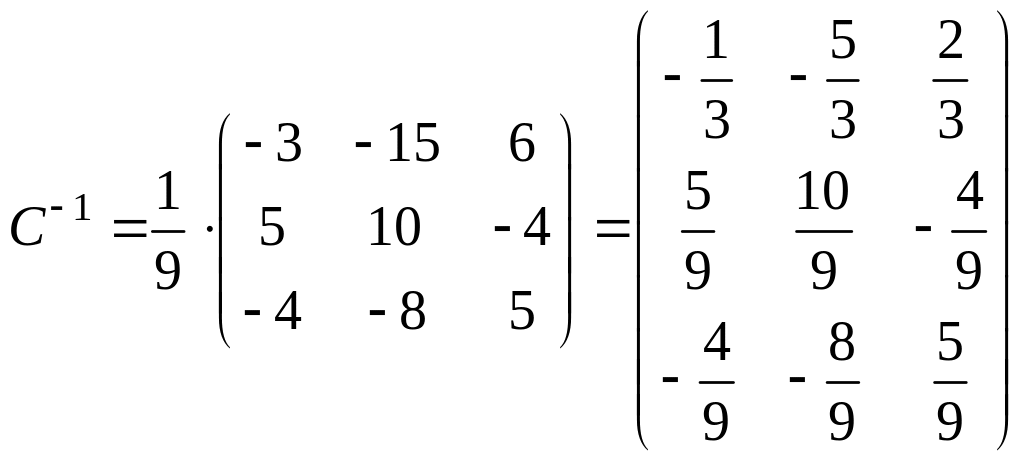 .
.
Матрицы
порядка больше
![]() удобнее искать с помощью элементарных
преобразований.
удобнее искать с помощью элементарных
преобразований.
Найдем
![]() другим способом – с помощью элементарных
преобразований:
другим способом – с помощью элементарных
преобразований:
.
По
определению
![]() ,
тогда:
,
тогда:
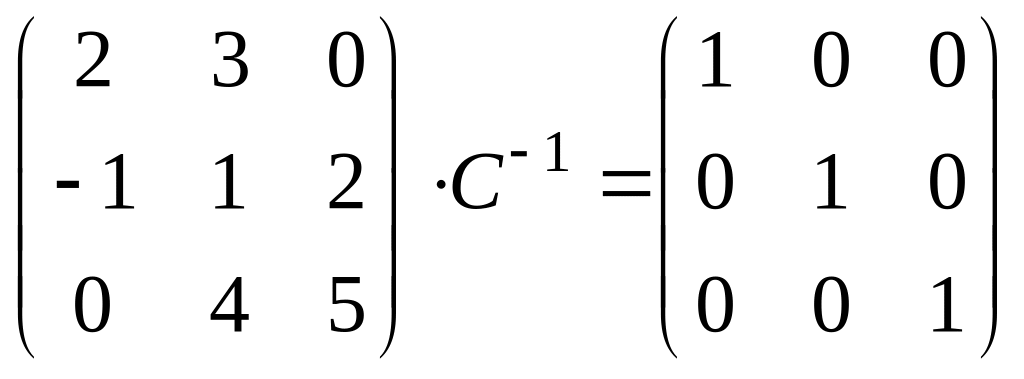 .
.
В результате элементарных преобразований получим в левой части равенства единичную матрицу. Преобразования должны проводиться одновременно над левой и правой частью равенства:
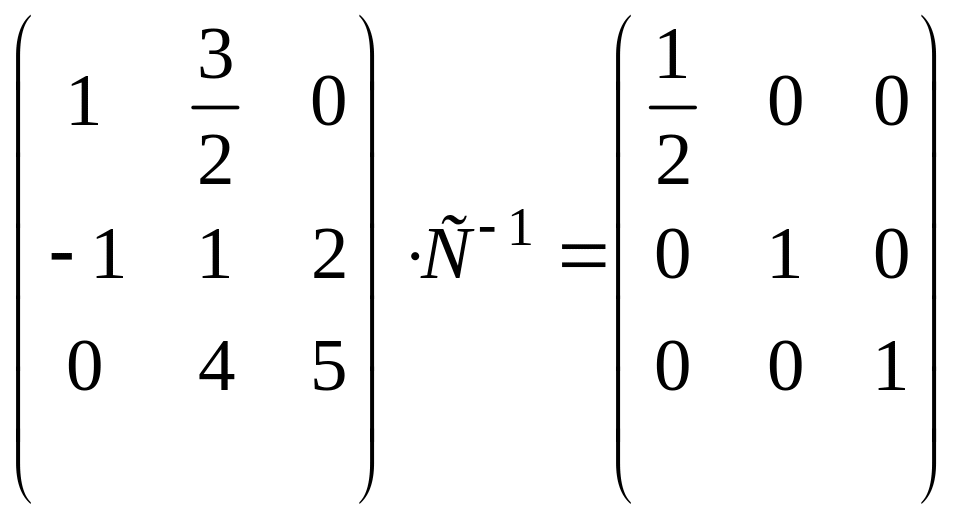
Получили
1 на месте элемента
![]() ,
прибавим первую строку ко второй.
,
прибавим первую строку ко второй.
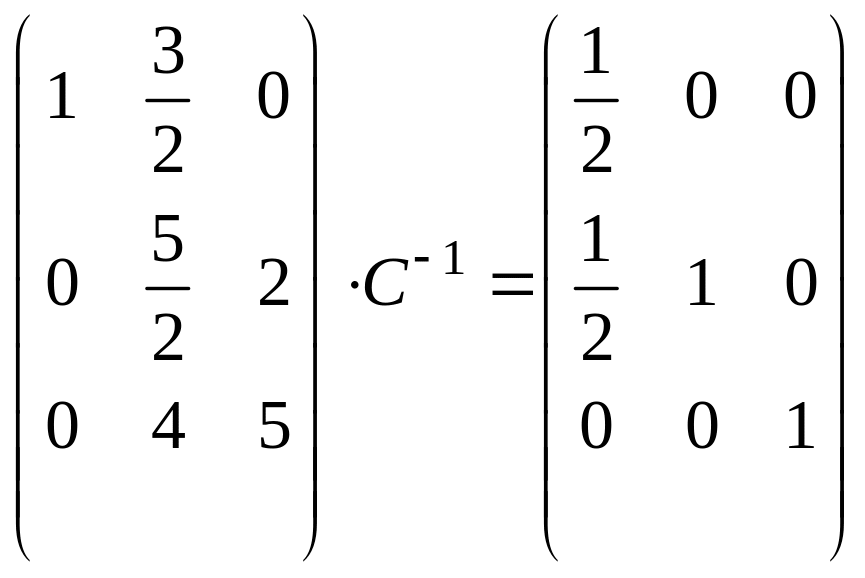 ;
;
разделим
вторую строку на
![]() :
:
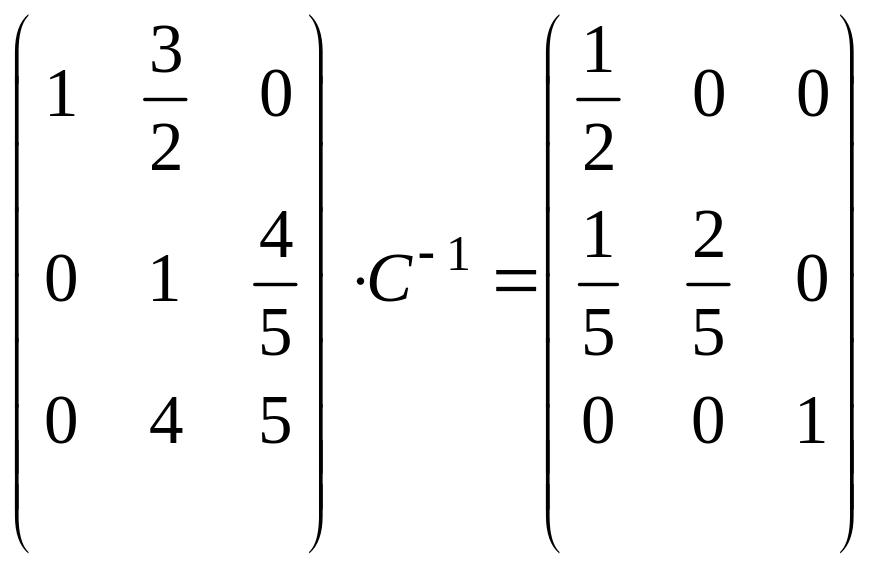 ;
;
вторую
строку, умноженную на
![]() ,
вычитаем из третьей:
,
вычитаем из третьей:
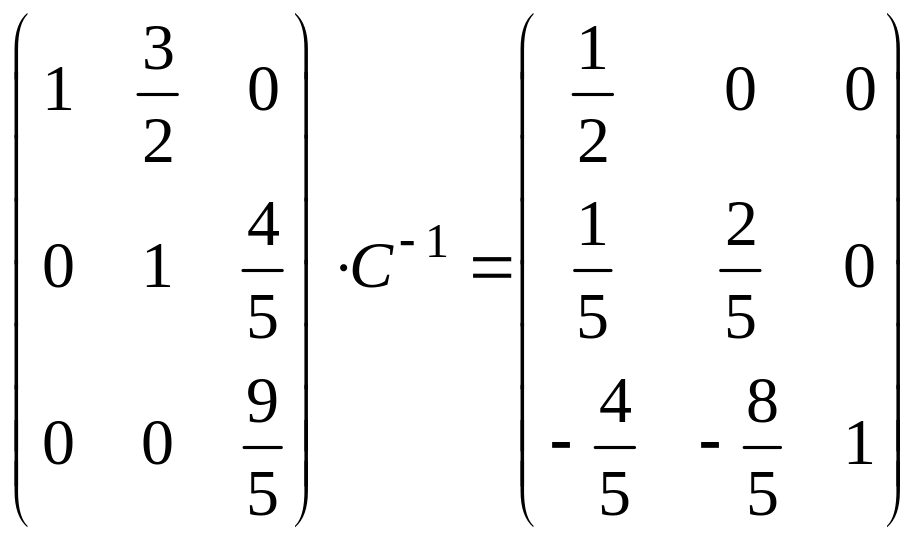 ;
;
третью
строку разделим на
![]() :
:
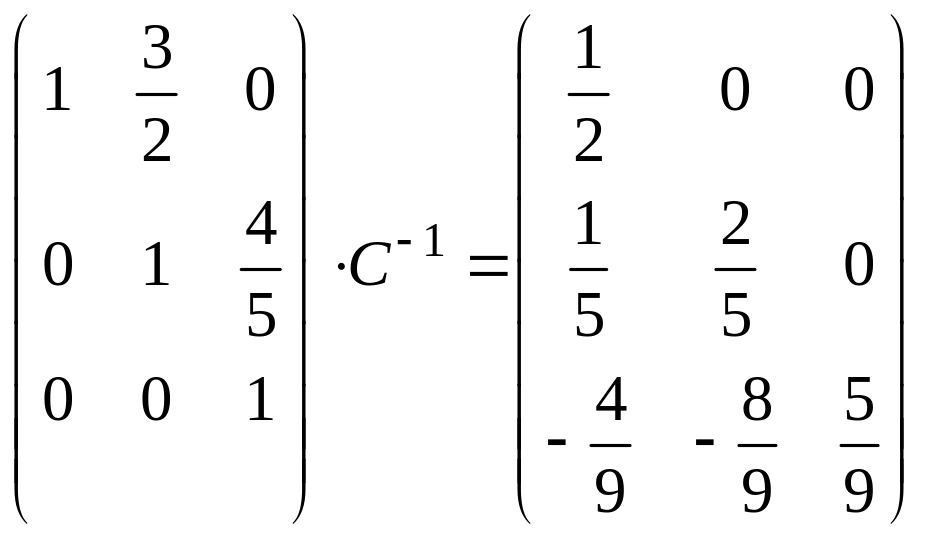 ,
,
получили
нули ниже главной диагонали. Получим
нули выше главной диагонали: третью
строку, умноженную на
![]() ,
вычтем из второй:
,
вычтем из второй:
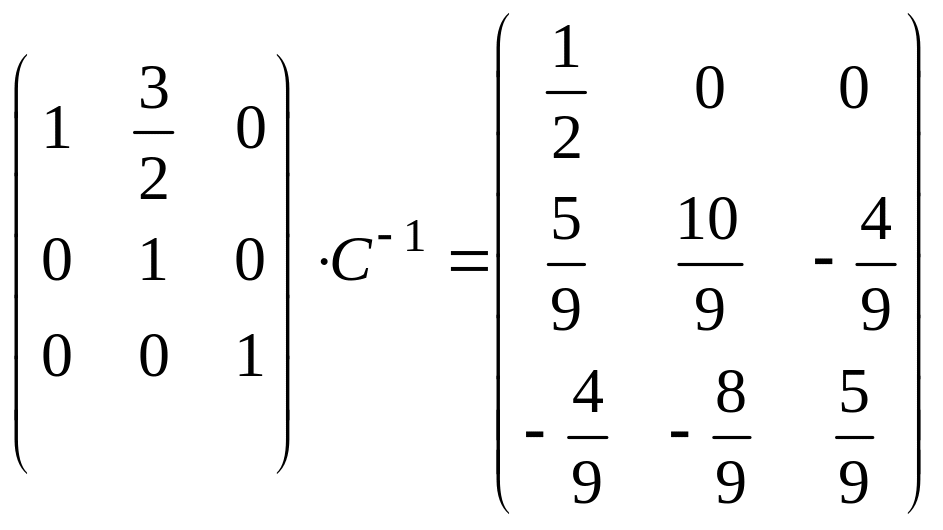 ;
;
вторую
строку, умноженную на
![]() ,
вычитаем из первой:
,
вычитаем из первой:
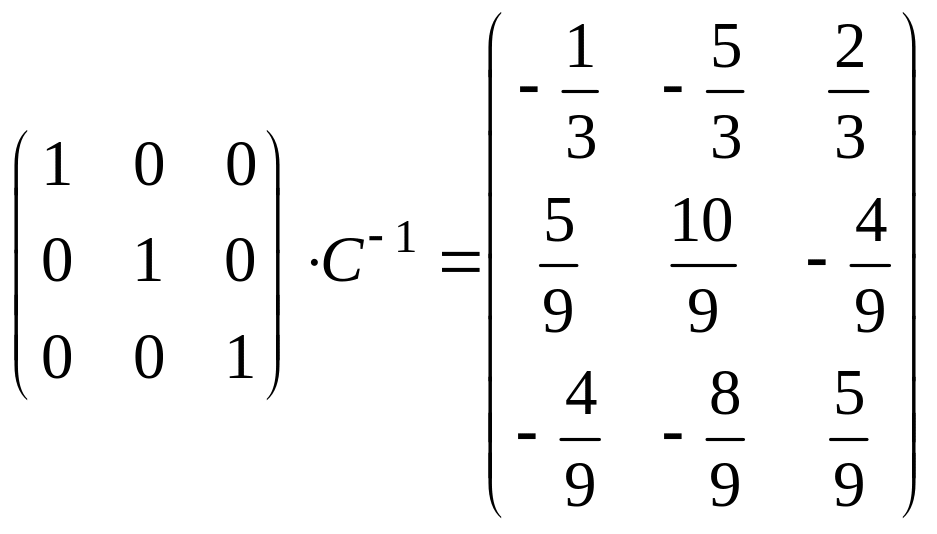 ,
,
слева
– произведение
![]() .
.
Итак,
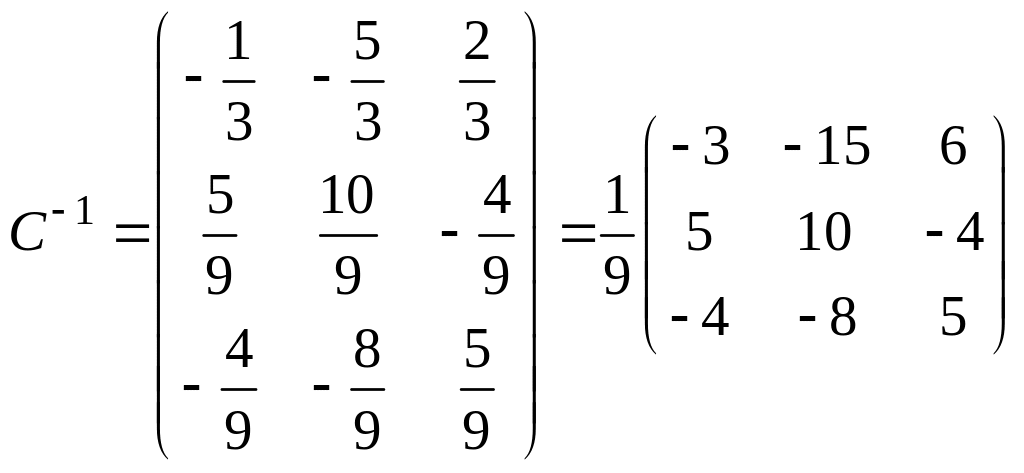 .
.
Задача
8.
Решить двумя способами систему:
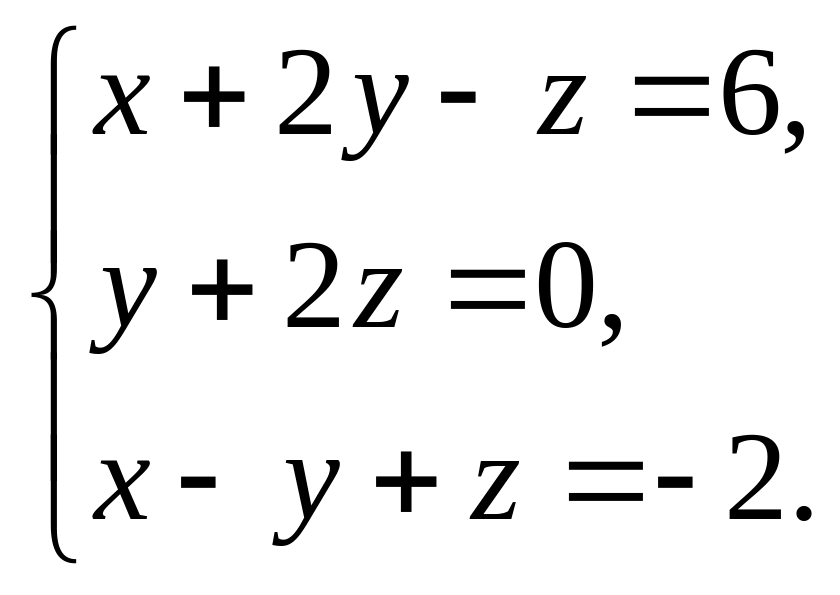
Решение.
1) По формулам Крамера:
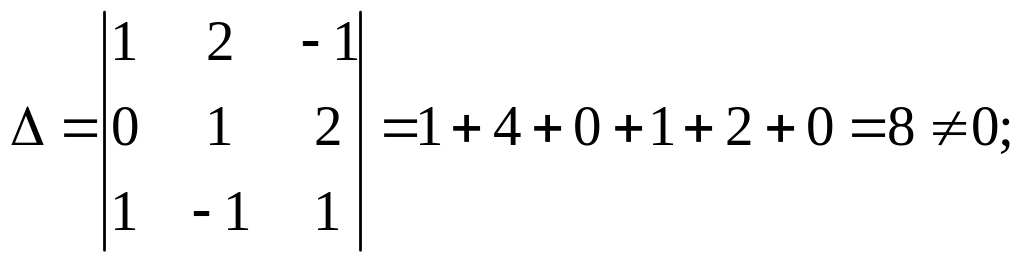
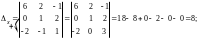
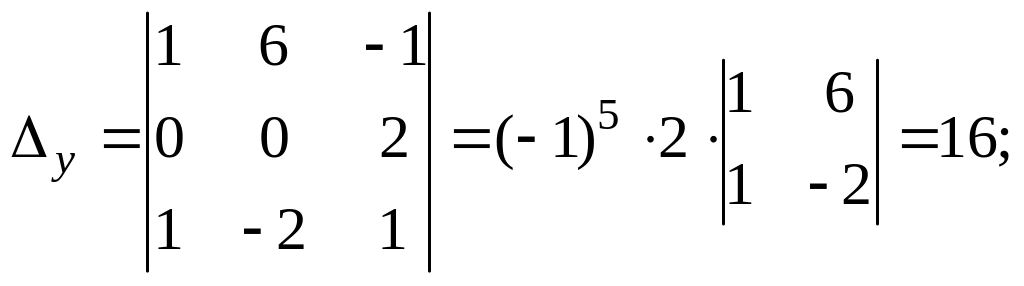
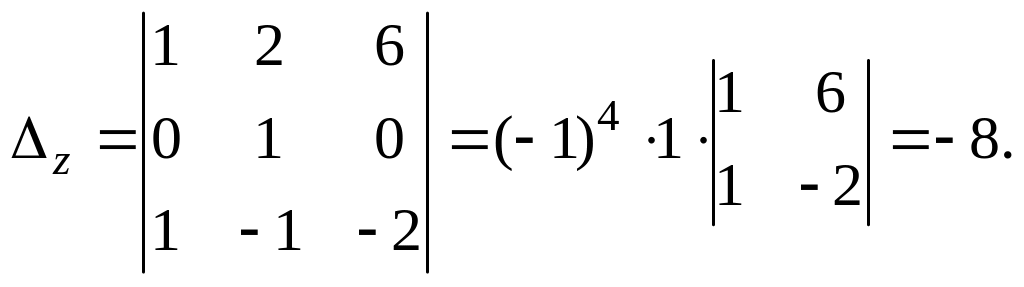
Неизвестные
системы:
![]() ,
,![]() ,
,
![]() .
.
Ответ:
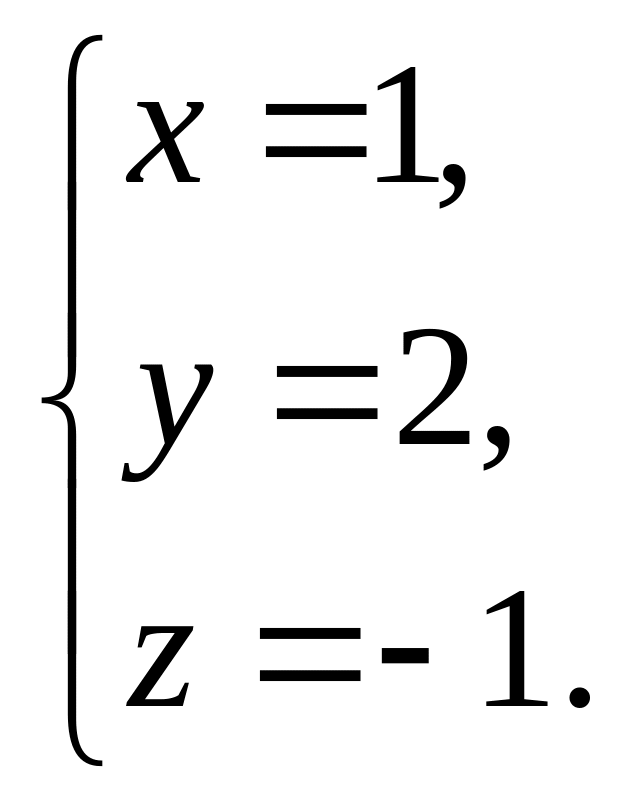
2) С помощью обратной матрицы:
![]() ,
,
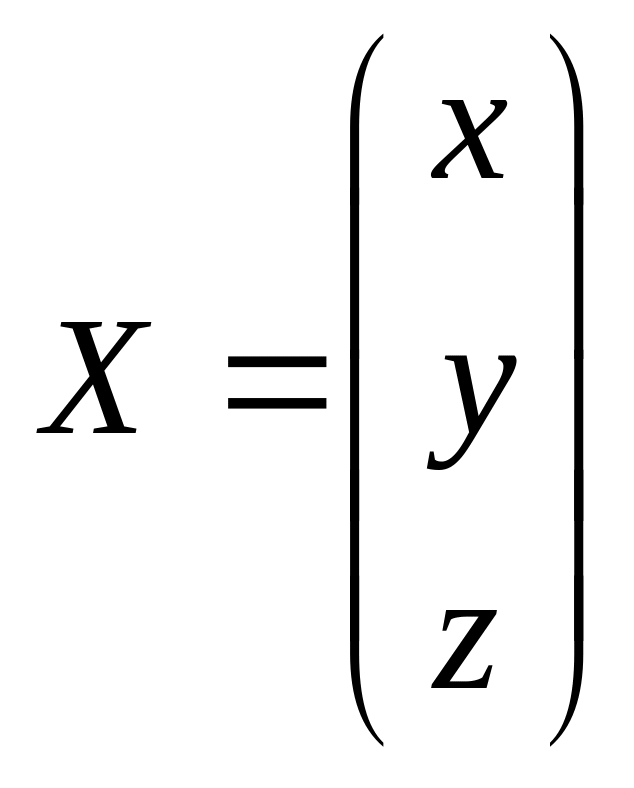 ,
,
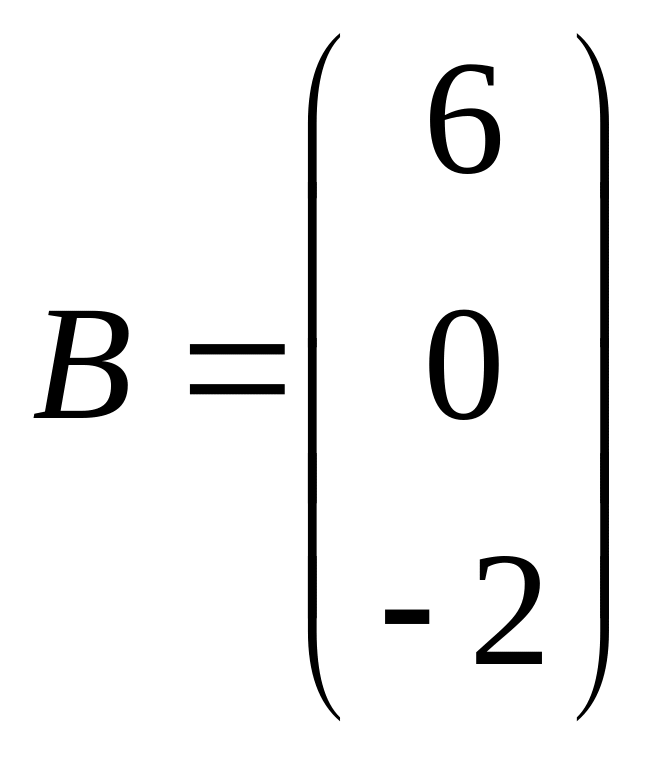 .
.
Найдем
матрицу
![]() :
:
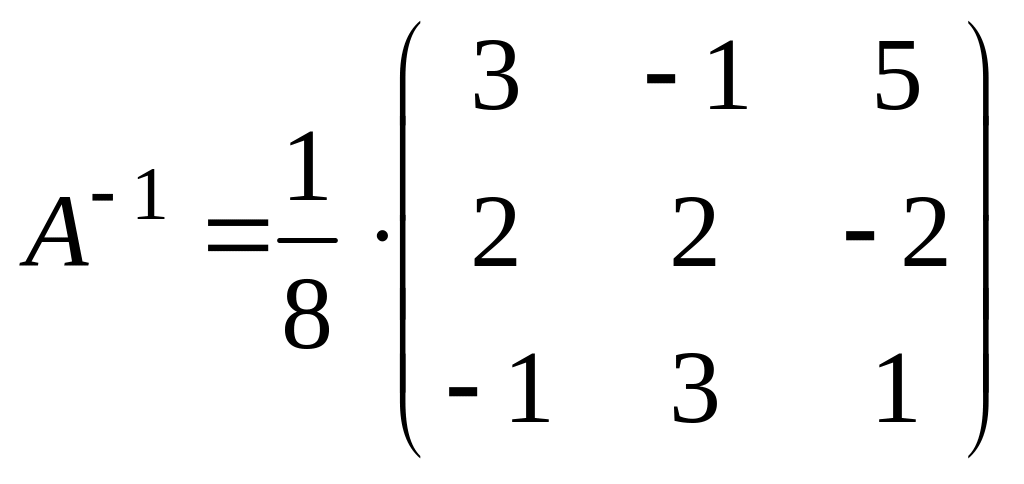 ;
;
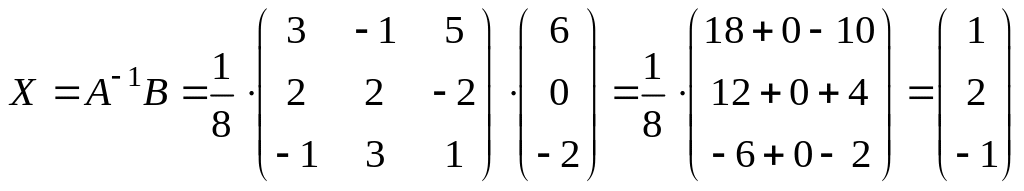 .
.
Итак,
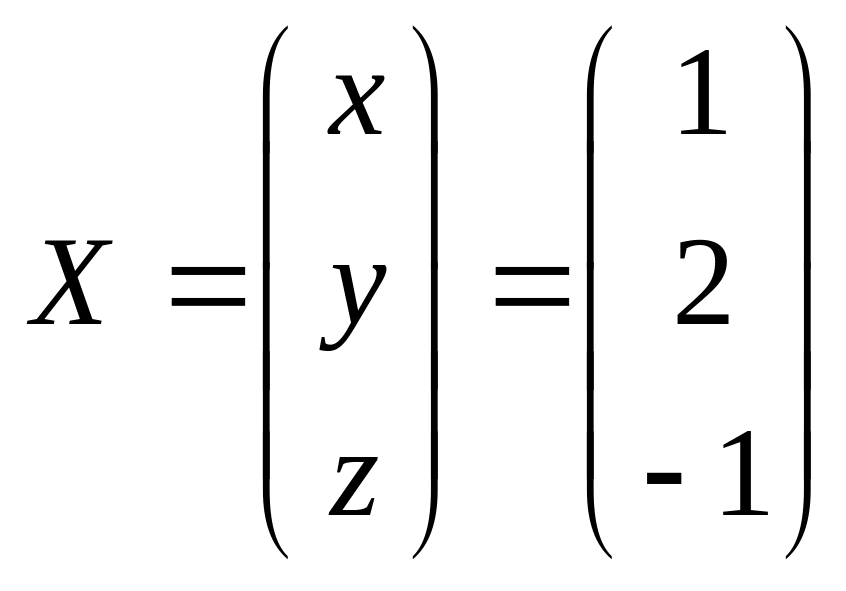 ,
из определения равенства матриц
,
из определения равенства матриц
Задача 9. Решить матричные уравнения
1.
![]() ;
2.
;
2.
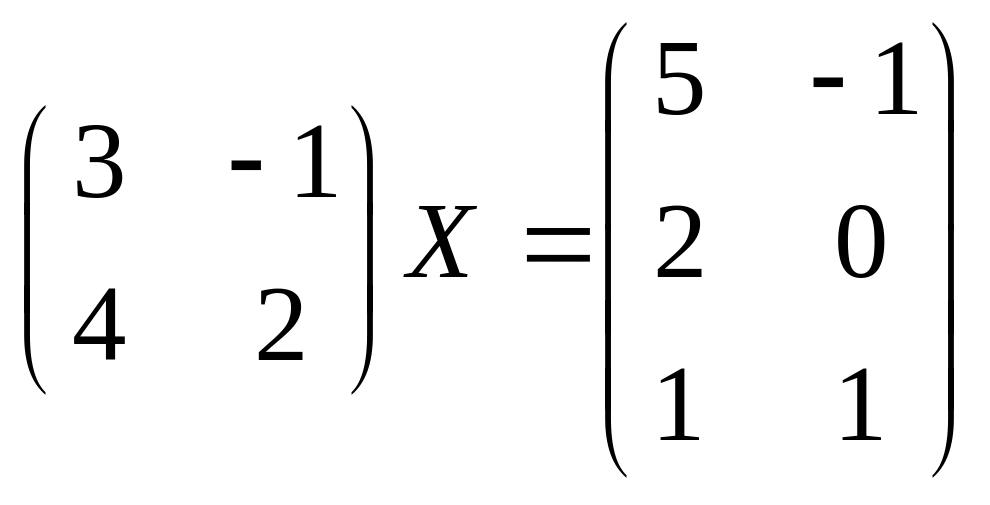
Решение.
Уравнение вида
![]() :
:
1. ![]() ;
;
![]() ;
;
![]() ,
так как
,
так как
![]() ,
то обратная матрица
существует.
,
то обратная матрица
существует.
Вычислим
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
тогда,
![]() .
.
Умножаем
уравнение
на
:
![]() ,
,
![]() ,
,
![]() ,
тогда
:
,
тогда
:
![]() .
.
Ответ:
![]() .
.
2.
,
 .
.
Обратная
матрица
,
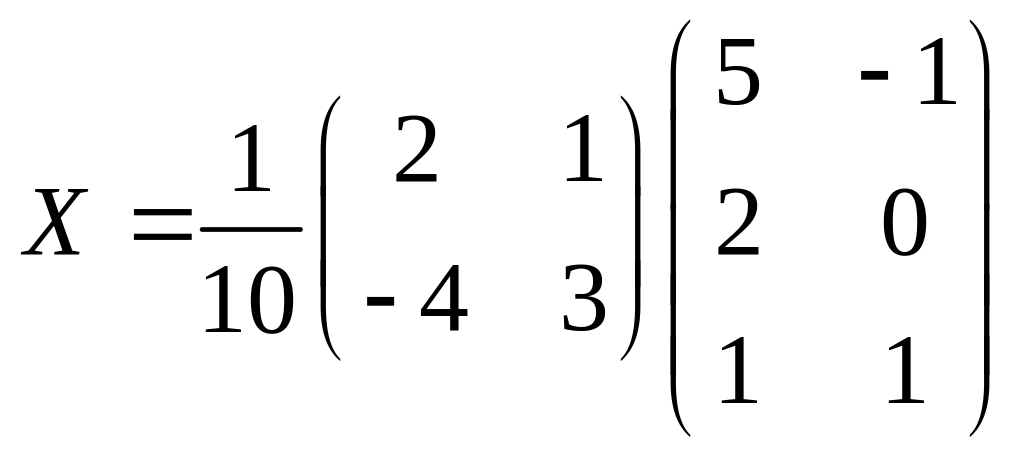 ,
произведение
,
произведение
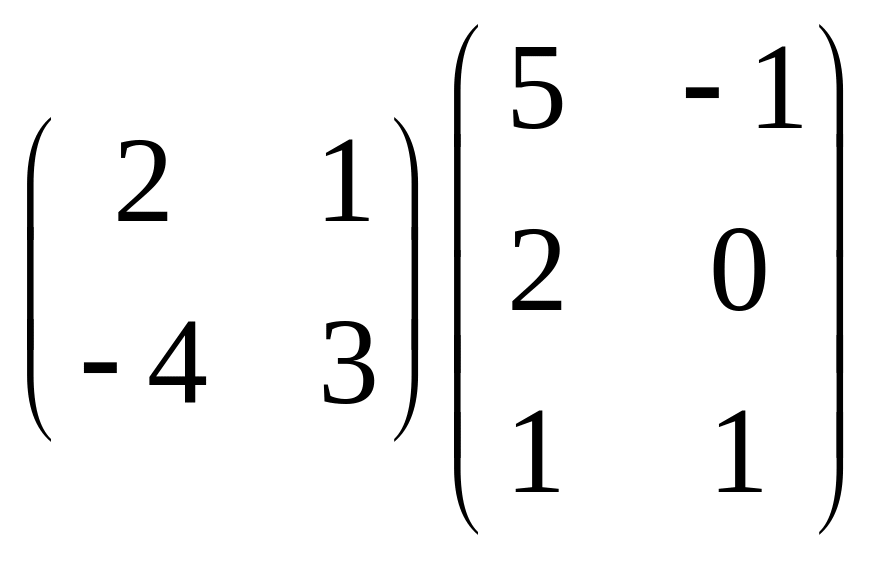 не
существует, так как матрицы не согласованы,
т.е.
не
существует, так как матрицы не согласованы,
т.е.
![]() не существует.
не существует.
Задачи для самостоятельного решения
Вычислить значения матричных многочленов.
1. ![]() .
Найти
.
Найти
![]() ,
если
,
если
![]() ,
,
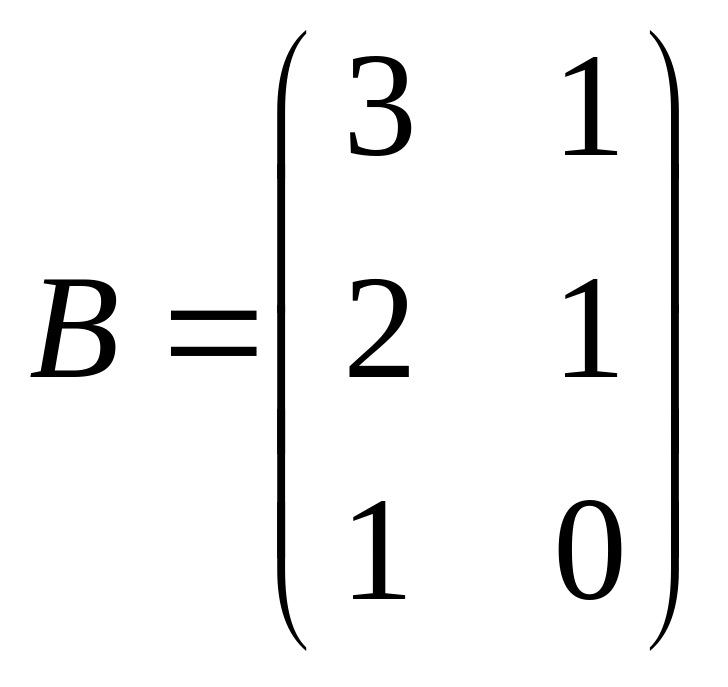 .
Ответ:
.
Ответ:
![]() .
.
2. Найти
![]() ,
,
![]() ,
,
 .
.
Ответ:
 .
.
3. Найти
,
если
,
![]() ,
,
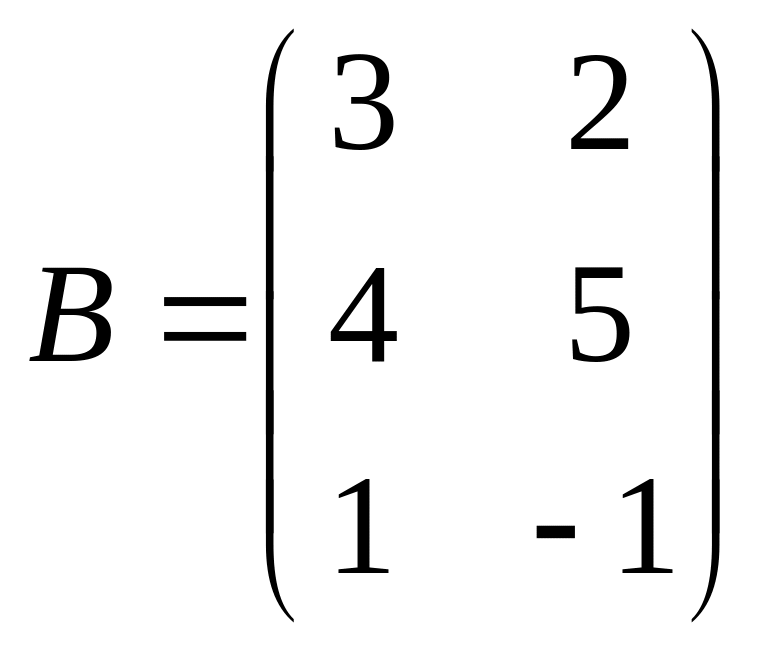 .
Ответ:
.
Ответ:
![]() .
.
4. Доказать,
что
является корнем многочлена
![]() ,
если
,
если
![]() ,
,
![]() .
.
5. Найти
![]() ,
если
,
если
![]() ,
,
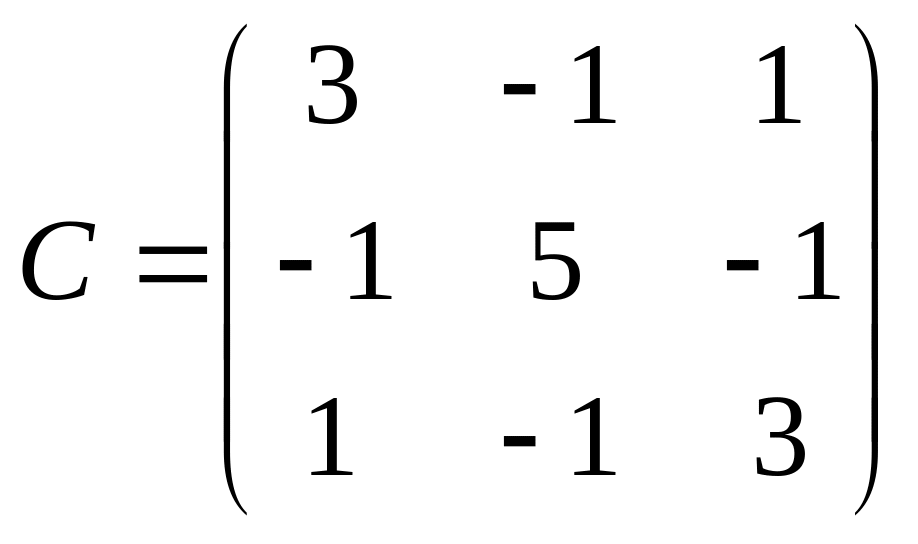 .
.
Ответ:
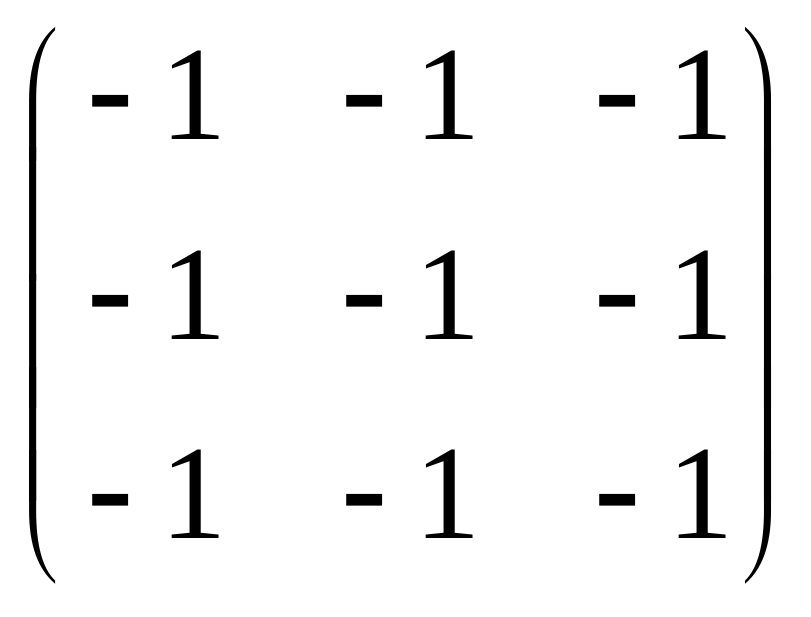 .
.
6. Найти
![]() ,
если
,
если
![]() ,
,
![]() .
.
Ответ:
![]() .
.
7. Найти
![]() ,
если
,
если
![]() ,
,
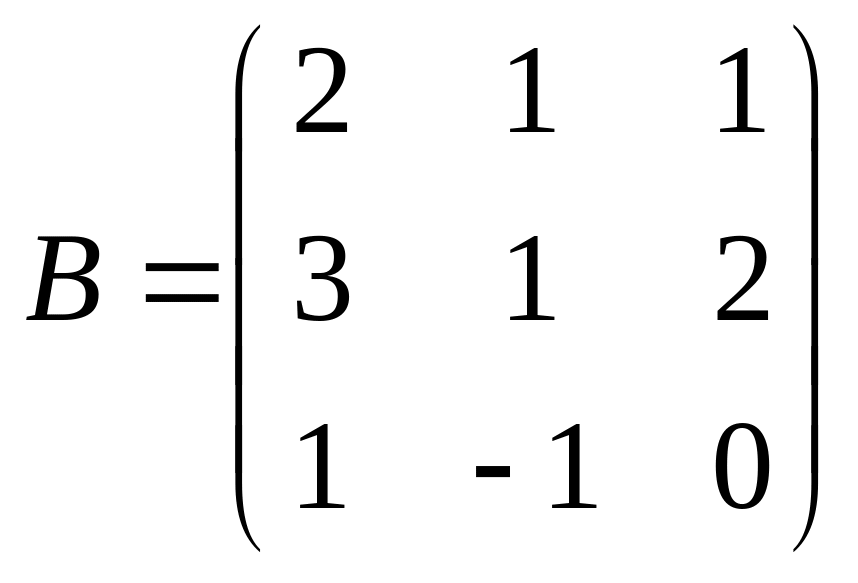 .
.
Ответ:
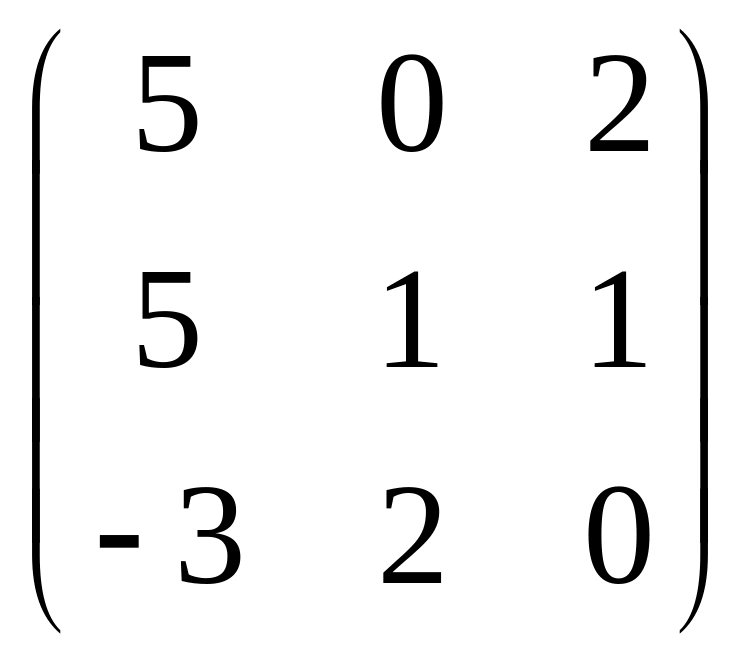 .
.
8. Доказать,
что
является корнем многочлена
![]() ,
если
,
если
![]() ,
,
![]() .
.
9. Найти
;
![]() ,
если
,
если
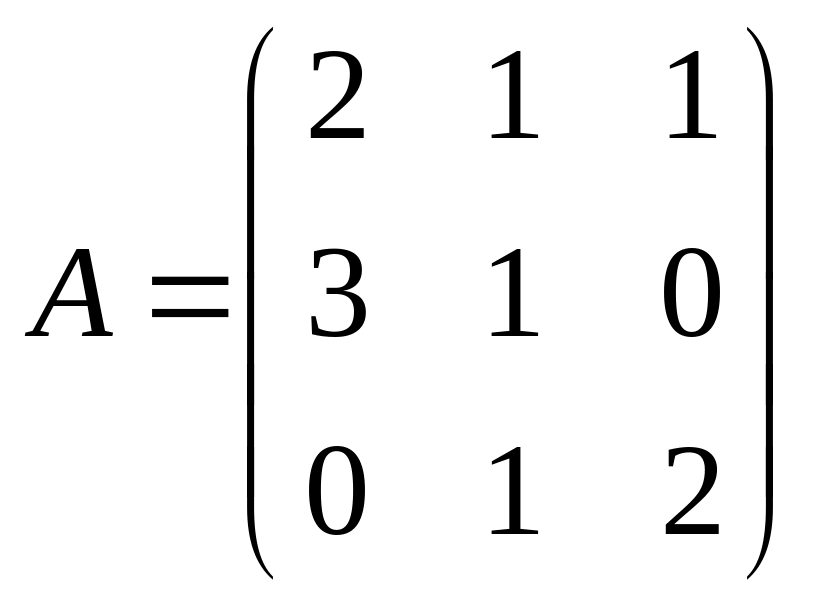 .
.
10. Доказать,
что
– корень многочлена
![]() ,
если
,
если
![]() ;
;
![]() .
.
11. Решить системы по формулам Крамера и с помощью обратной матрицы :
1.
|
2.
|
3.
|
4. |
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
Ответ:
1. ![]() 2.
2. 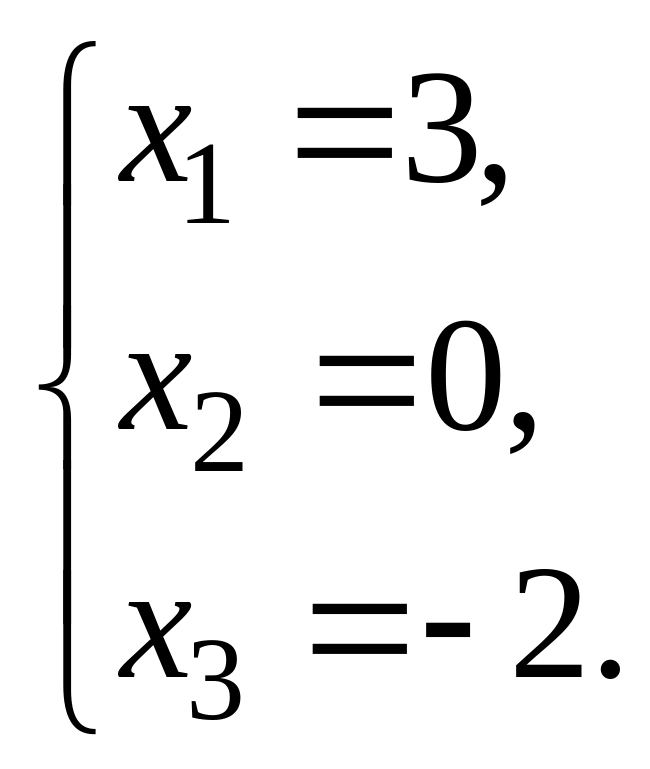 3.
3. 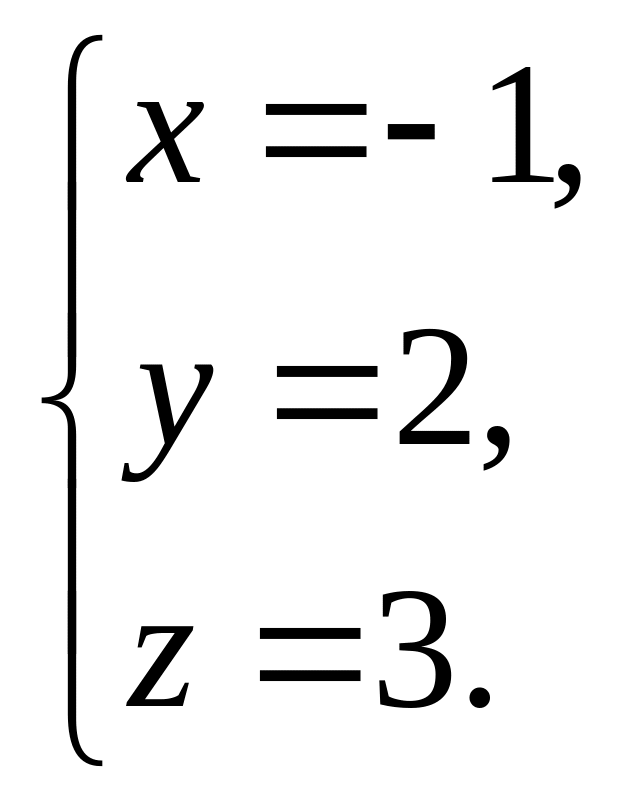 4.
4. 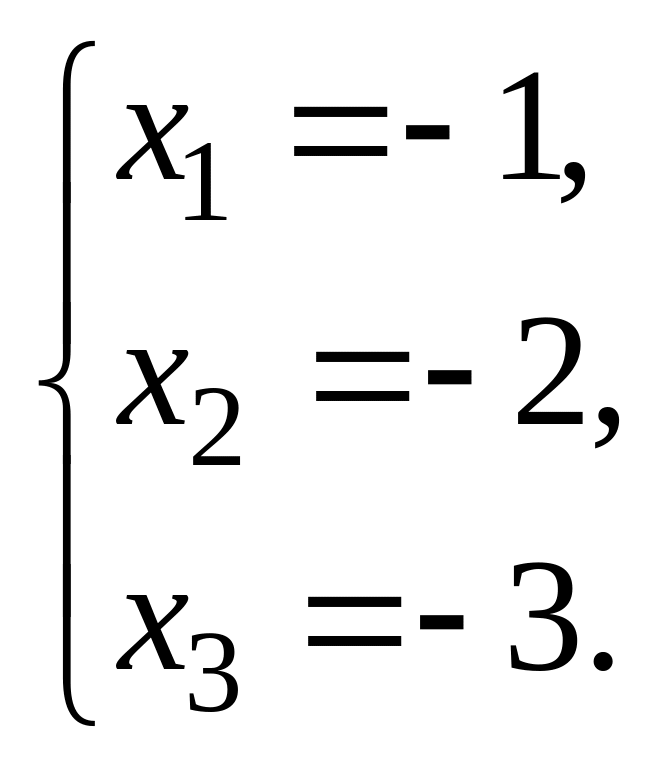 5.
5. 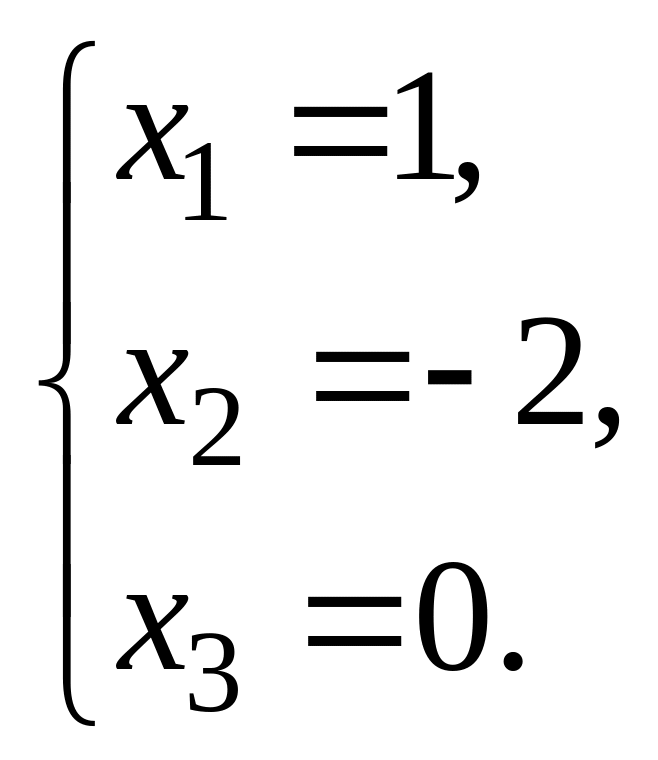 6.
6. 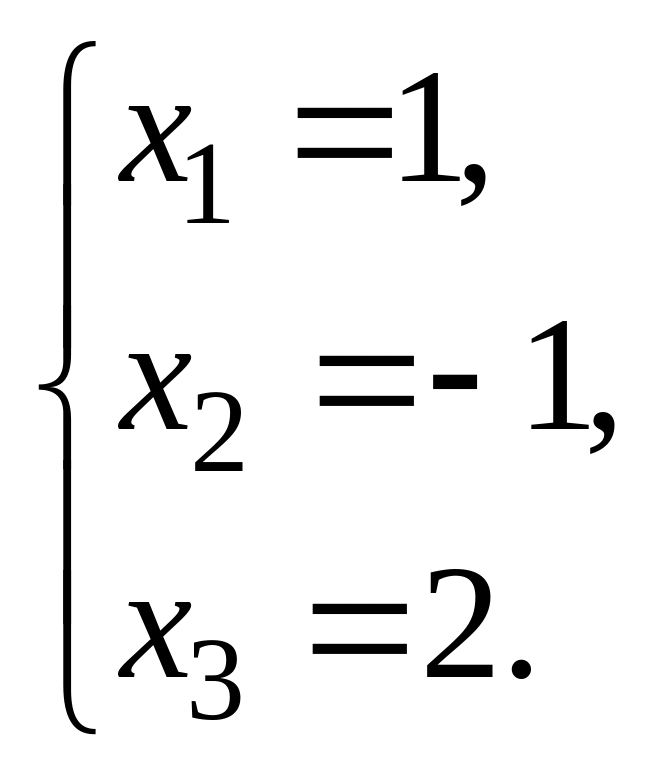 7.
7. ![]() 8.
8. 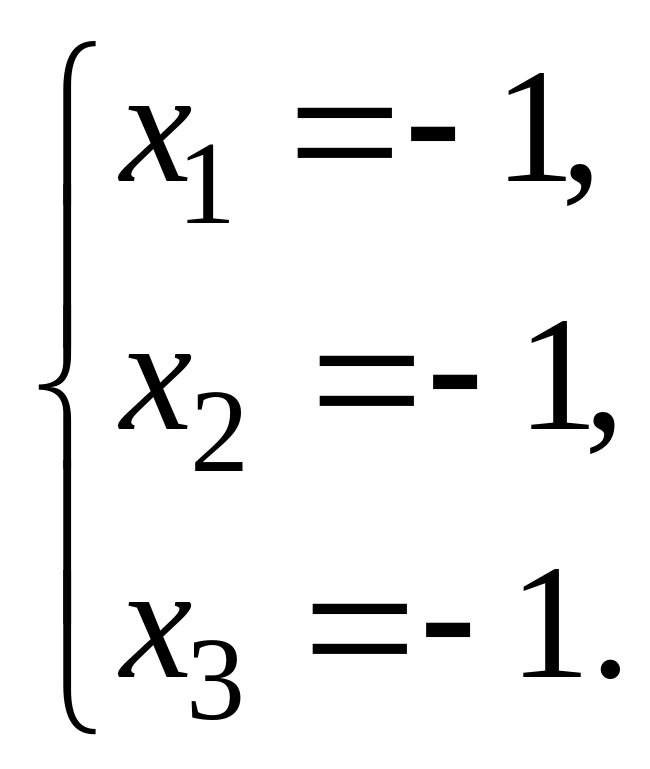 9.
9. 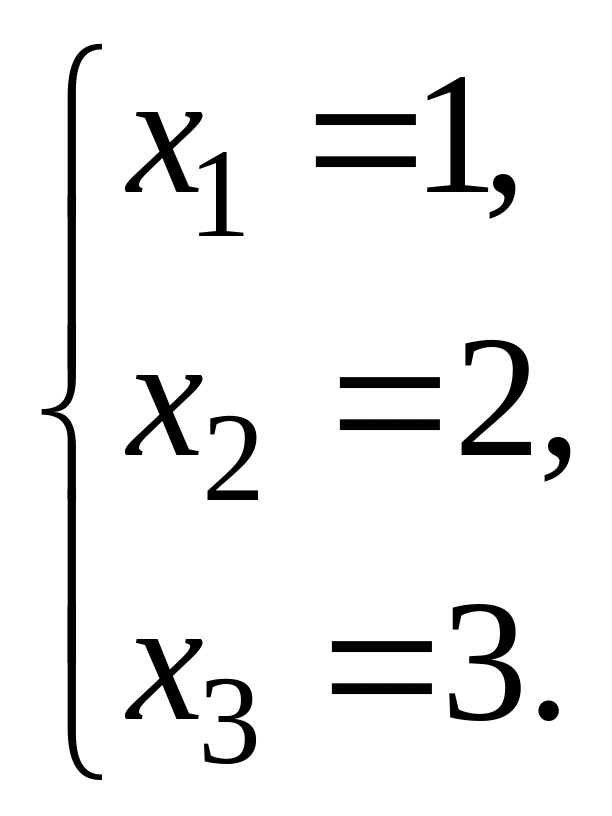 10.
10. 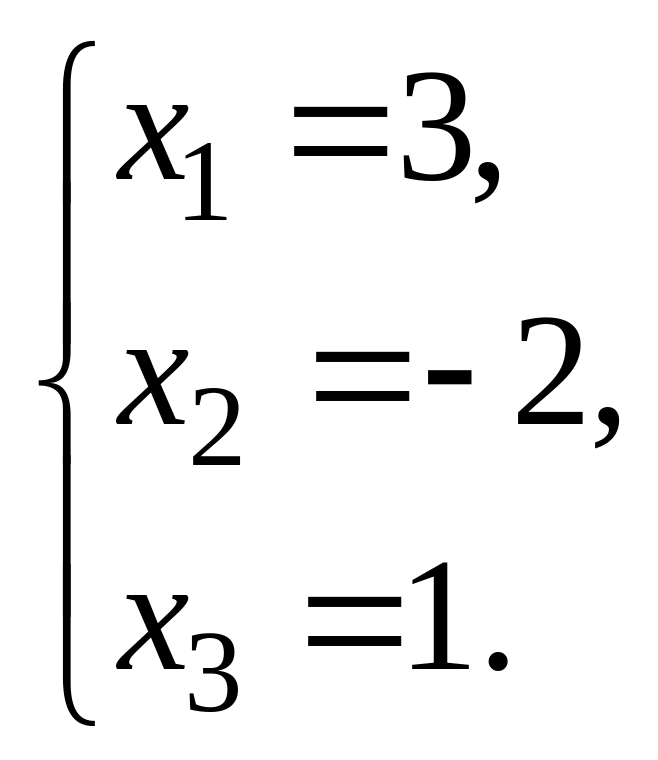
12. Решить матричные уравнения
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
Ответ:
1. ![]() 2. не
существует, так как размерность
2. не
существует, так как размерность
![]() ,
а размерность
–
3.
,
а размерность
–
3. ![]() 4.
4. ![]() 5.
5. ![]() 6.
6. ![]() 7. не
существует, так как
7. не
существует, так как
![]() 8.
8. ![]()

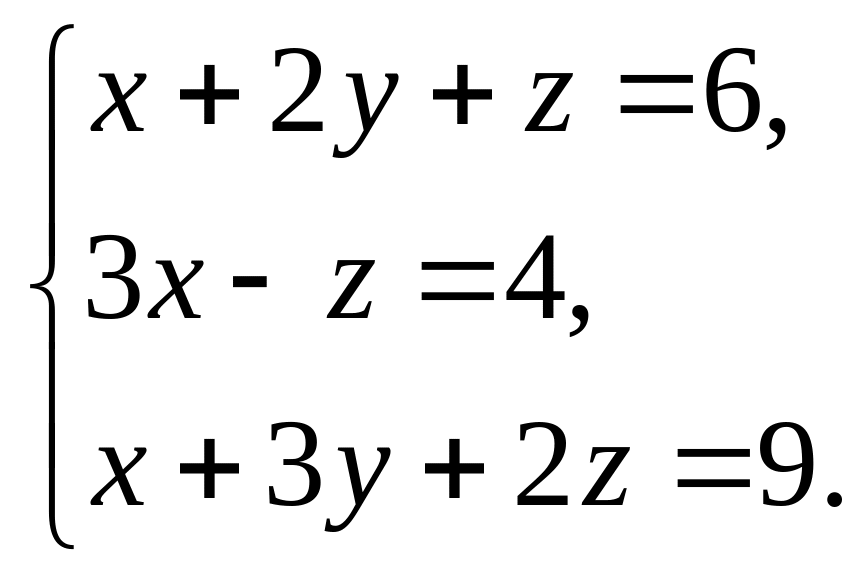
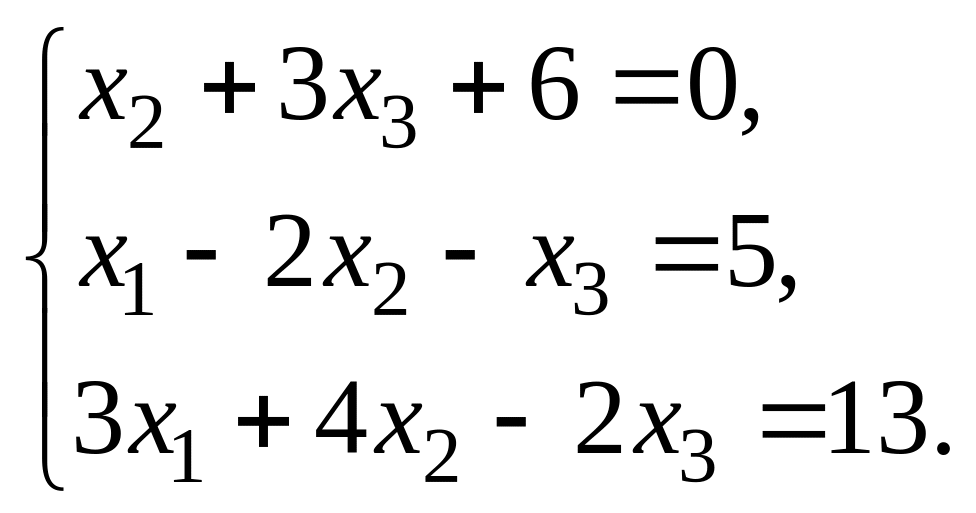
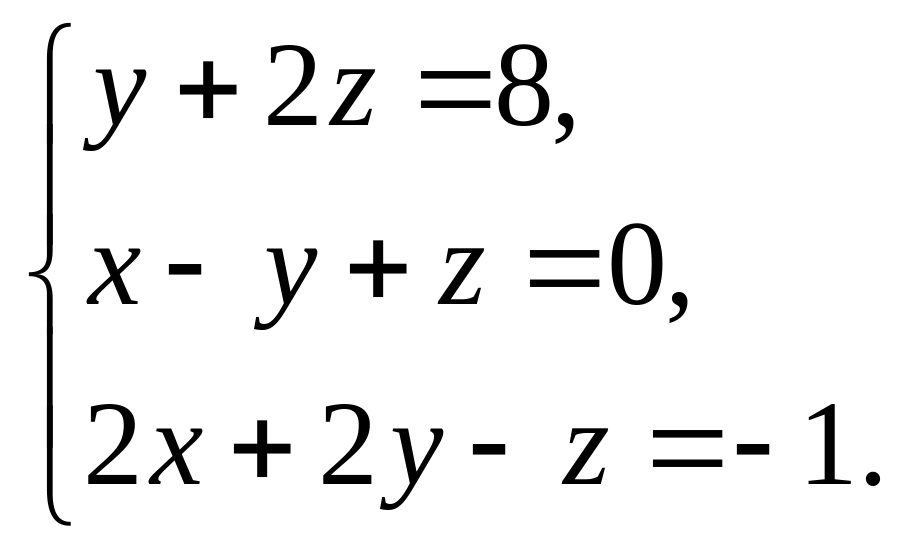
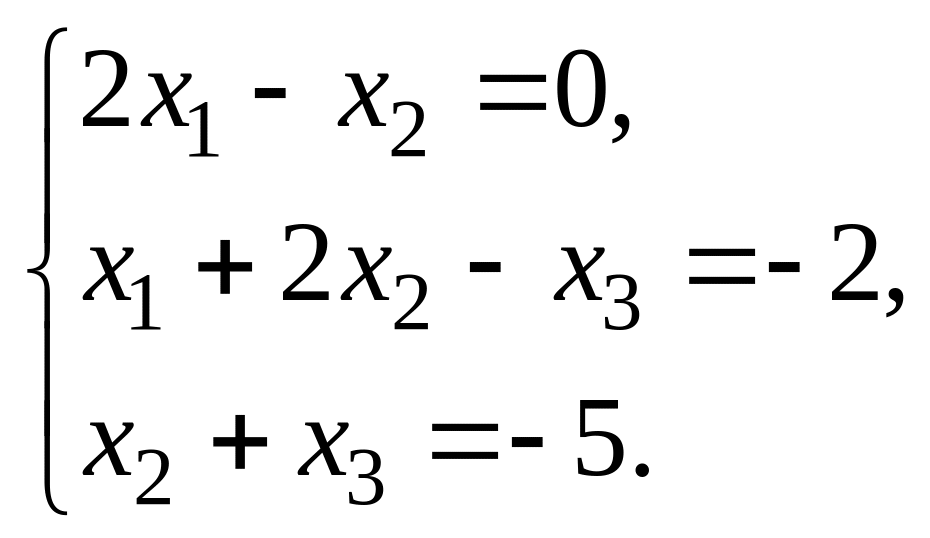
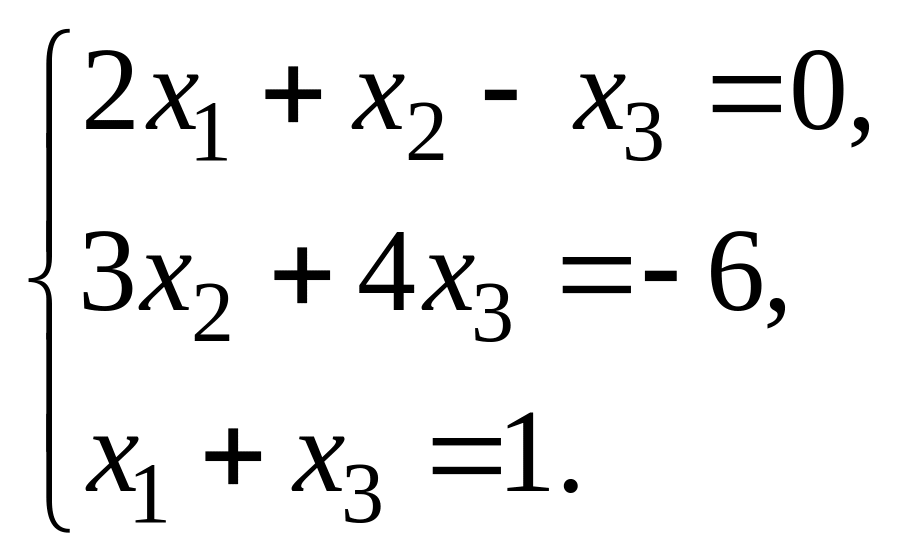
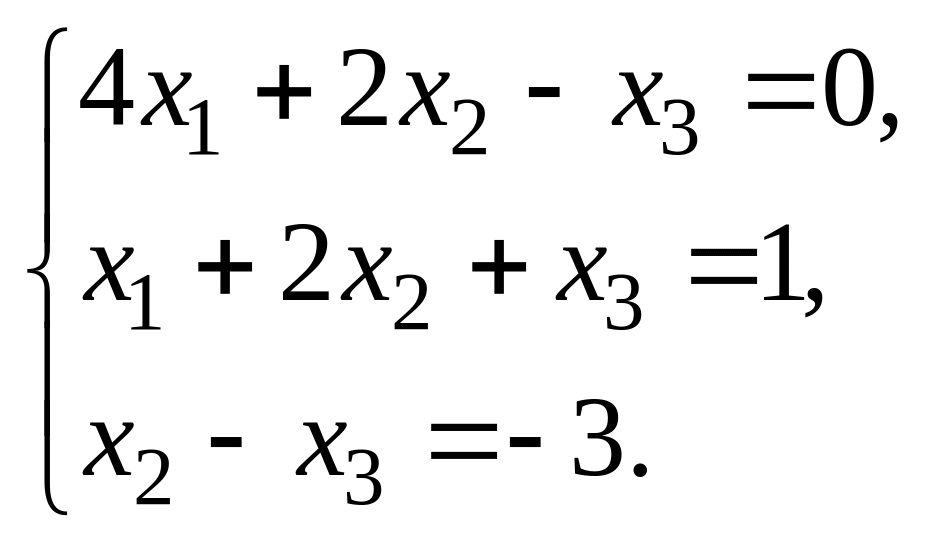

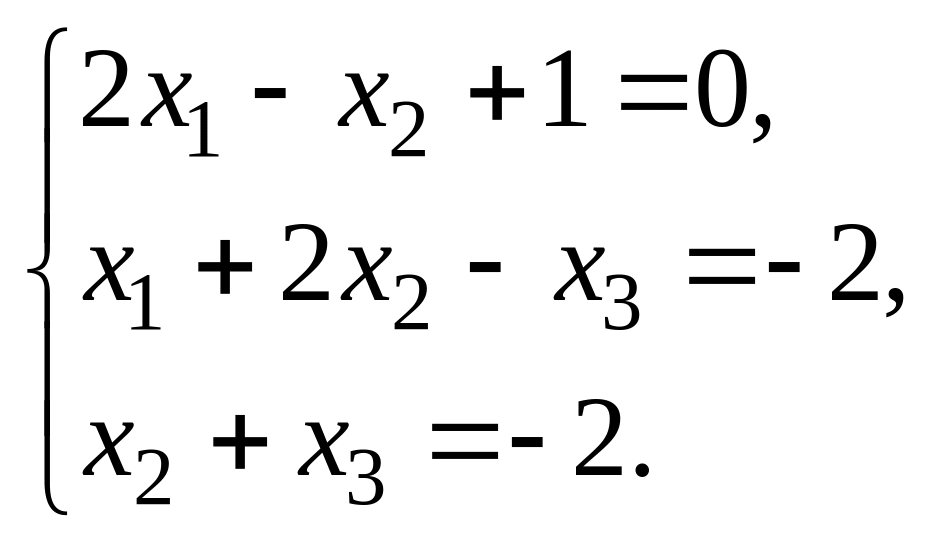

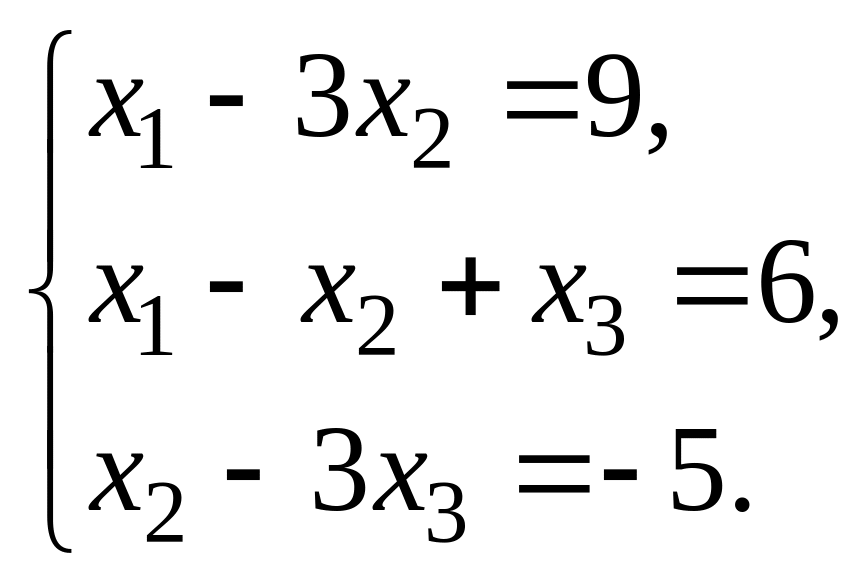
 ;
;