Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Таврический Национальный Университет им. В.И. Вернадского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Sistemy_koordinat_v_teor_mehanbroshyura.doc

Скачиваний:

Добавлен:

16.11.2019

Размер:

1.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Примеры.

1. Три семейства параллельных прямых образуют

декартову систему координат, если прямые,

принадлежащие разным семействам ортогональны

между собой.

2. Цилиндрическая система координат состоит из

одного семейства окружностей и двух семейств

прямых.

3. Сферическая система координат состоит из двух

семейств окружностей и одного семейства

прямых.

Замечание. В приведенных примерах координатные кривые ортогональны между собой. Свойство ортогональности здесь случайное, в общем случае координатные кривые не обязаны быть ортогональными.

Если пространство снабжено системой координат, то в каждой точке пространства три вектора, касательные к координатным линиям, образуют координатный базис. Система координат и соответствующее ей множество координатных базисов взаимнооднозначно определяют друг друга:

-15-

линии, огибающие векторы, принадлежащие

координатным базисам, образуют координатные линии; касательные к координатным линиям векторы в каждой точке их пересечения образуют координатные базисы.

Координатные базисы частный случай общих базисов, рассмотренных в предыдущем разделе, поэтому они подчиняются тем же соотношениям, что и базисы вообще. Вместе с тем, они играют особую роль в дифференциальной геометрии метрических пространств. Для того, чтобы отличать координатные базисы от всех остальных, скалярное произведение векторов координатных базисов обозначают вместо (см. определяющую формулу (3.2)) специальным символом и называют метрическим тензором.

, (4.1)

если - координатный базис.

Рассмотрим две точки и метрического пространства. Вектор , соединяющий эти точки, при имеет контравариантные компоненты , т.е. в координатном базисе его можно представить формулой

Поэтому

-16-

Пять последних уравнений составляют замкнутую систему однородных линейных уравнений относительно искомых и . Единственным решением этой системы, удовлетворяющим начальным значениям

согласно условиям леммы, является

Первое уравнение при имеет единственное решение . По условию леммы , поэтому , что и доказывает лемму.

Теорема. Значения кривизны и кручения кривой как функции длины дуги однозначно определяют форму кривой, независимо от ее положения в пространстве.

Доказательство. Общее решение уравнений Френе (5.12 b, c, d) при заданных по условию теоремы

-33-

4. Круглая винтовая линия с постоянным шагом и

только такая линия имеет постоянные, отличные от

нуля значения кривизны и кручения.

Выше было отмечено, что по структурным функциям и кривой можно однозначно “восстановить” форму кривой с точностью до ее положения в пространстве. Приведем доказательство этого утверждения, но прежде докажем следующую лемму.

Лемма. Ортонормированность подвижного базиса в каждой точке кривой обеспечивается его ортонормированностью в одной (начальной точке).

Доказательство. Введем обозначения

Используя уравнения Френе (5.12 b, c, d) легко получить уравнения для введенных функций

-32-

Так как совпадает с квадратом расстояния (или, как в этом случае принято обозначать ) между точками и пространства, то последнее равенство можно переписать в следующем виде:

(4.2)

Равенство (4.2) в дифференциальной геометрии лежит в основе описания метрических свойств пространства и носит название фундаментальной или основной квадратичной формы пространства. Это и объясняет, почему правая часть (4.1) получила названия метрического тензора.

Поскольку множество координатных базисов непрерывно (векторы координатных базисов являются касательными векторами к гладким координатным линиям), то и метрический тензор непрерывная функция точки пространства. Знание метрического тензора или фундаментальной формы позволяет в координатной системе легко восстановить координатный базис:

1) направления базисных векторов являются

касательными к координатным линиям;

2) квадраты их модулей и углы между базисными

векторами находятся из равенства (4.1).

Пусть имеются две системы координат, связанные друг с другом преобразованиями

(4.3)

Дифференцируя эти равенства, получаем

-17-

(4.4)

Так как преобразование координат взаимно однозначное, то

(4.5a,b)

Отсюда следует, что матрица преобразования является обратной к матрице . Сопоставляя равенства (3.20) с преобразованиями (4.4), получаем, что преобразование координат эквивалентно преобразованию координатных базисов, осуществляемому матрицей

(4.6)

Сводка основных положений данного раздела.

1. Геометрия пространства в произвольной системе координат определяется его квадратичной формой

2. Система координат и координатный базис

-18-

Она проходит из нижней полуплоскости в верхнюю, если , и из верхней полуплоскости в нижнюю, если . Точка является точкой перегиба кубической параболы. При смещении от вдоль кривой на расстояние отклонение кубической параболы от оси так же является малой величиной не менее третьего порядка

Если кривизна кривой связана с ее отклонением от касательной прямой в соприкасающейся плоскости, то кручение кривой ассоциируется с ее изгибанием в другой, спрямляющей плоскости.

Изложенное здесь “осмысление” функций и основано на “анатомии” кривой в малой окрестности точки . Другой подход к их пониманию связан с вращением подвижного базиса (см. следующий раздел).

Примеры линий в пространстве.

1. Линия является прямой в том, и только том случае,

если .

2. Если и только в этом случае, все точки

линии принадлежат одной плоскости (плоская

кривая).

3. У окружности и только окружности кручение

равно нулю, а

-31-

т.е. исследуемая кривая и окружность расходятся на малую величину не менее третьего порядка и, следовательно, касание окружностью кривой имеет порядок не менее двух. В этом заключается причина, по которой величина интерпретируется как радиус кривизны кривой.

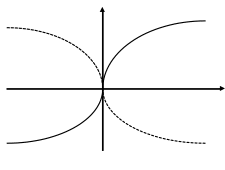
Рассмотрим теперь проекцию кривой на спрямляющую плоскость . Из формул (5.14a, c) следует, что эта проекция имеет вид кубической параболы (см. рис.3)

Рис. 3

-30-

в каждой точке пространства взаимно

однозначно определяют друг друга:

а) направление вектора является касательным к

- ой координатной линии;

б) модули векторов базиса и углы между ними

определяются формулой

в) координатная линия системы координат

является огибающей соответствующего вектора

координатного базиса.

3. Координатный базис и дополняющий его

базис взаимно однозначно определяют

друг друга

4. Любой вектор может быть представлен своими

ковариантными или контравариантными

компонентами

И наоборот, компоненты вектора определяются

в координатных базисах формулами

Для любых векторов и имеют место

равенства

-19-

6. Если две системы координат и

связаны между собой взаимно однозначным

преобразованием

то имеют место равенства

матрице преобразования координат

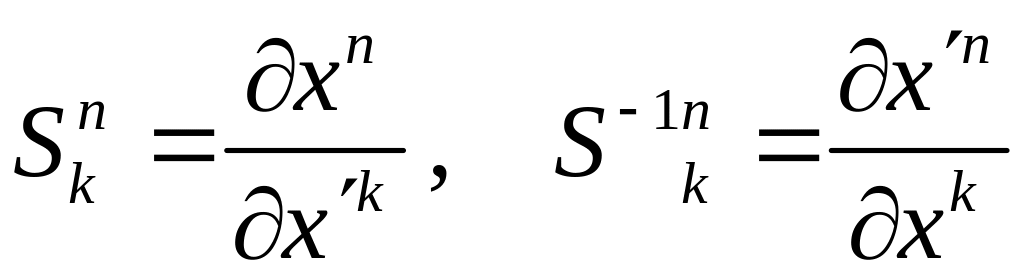
нижний индекс нумерует строки, а верхний

столбцы.

7. Координатные базисы различных систем

координат связаны между собой соотношениями

-20-

В точке ось касается кривой. При смещении вдоль кривой на величину кривая и ось расходятся на расстояние . Поэтому

т.е. кривая и ось расходятся на малую величину второго порядка. Именно это и дает основание говорить о касании 1-го порядка осью исследуемой кривой в точке .

Проведем теперь окружность радиуса с центром в точке на оси , так что . При смещении вдоль кривой окружность и кривая расходятся на расстояние . Вычислим это расстояние. Имеем

Поэтому

-29-

Проектируя вектор на направления и , получаем

(5.14a,b,c)

Величина радиуса кривизны исследуемой кривой в точке является естественным масштабом для измерения и сравнения значений и других длин в ее окрестности . Из (5.14a), например, находим, что в линейном приближении