МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

УКРАИНЫ

ТАВРИЧЕСКИЙ НАЦИОНАЛЬНЫЙ

УНИВЕРСИТЕТ им. В.И. ВЕРНАДСКОГО

КАФЕДРА ТЕОРЕТИЧЕСКОЙ ФИЗИКИ

Арифов Л.Я., Гопман А.Б.

СИСТЕМЫ КООРДИНАТ

В ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ

Учебные материалы по изучению учебной дисциплины ”Теоретическая механика” для студентов 2 курса дневной формы обучения 6.070100 ”физика” образовательно – квалификационного уровня ”бакалавр” профессионального направления подготовки 0701 ”физика”.

Симферополь 2004

Печатается по решению научно – методического совета ТНУ им. В.И.Вернадского

От 12 ноября 2004 года

Системы координат

в теоретической механике

Учебные материалы по изучению учебной дисциплины ”Теоретическая механика” для студентов 2 курса дневной формы обучения 6.070100 ”физика” образовательно – квалификационного уровня ”бакалавр” профессионального направления подготовки 0701 ”физика”.

Арифов Леннур Ягъя.,

Гопман Алексей Борисович

Редактор Василенко Н.А.

Подписано к печати Формат 60х84\46 Бумага тип ОП

Объём пл. Тираж 50экз. Заказ Бесплатно

95007 Г. Симферополь, проспект им. Академика

В.И. Вернадского 4, Таврический национальный университет им. В.И. Вернадского

что подгруппа

3. Докажите, что матрица

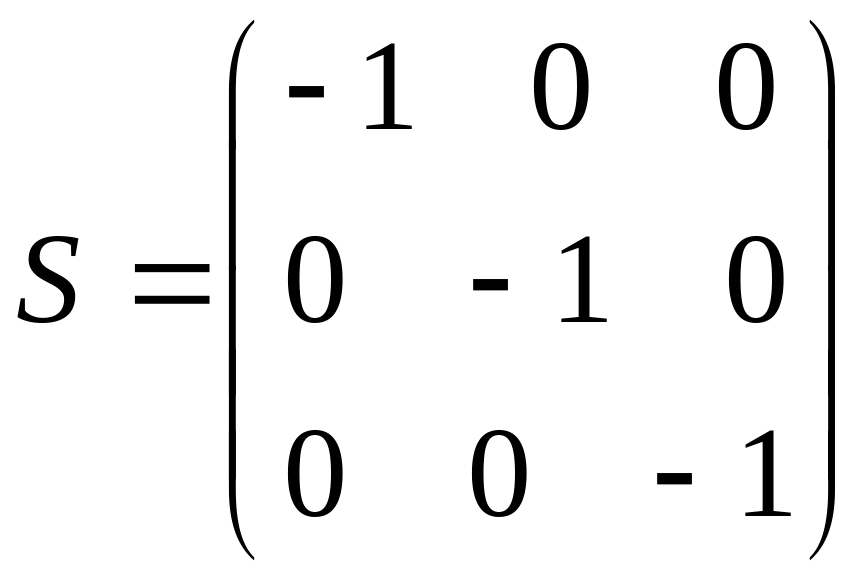
вместе с обратной ей матрицей образуют

дискретную группу зеркального отражения.

4. Покажите, что

5. Найдите вектор угловой скорости вращения

координатных базисов цилиндрической и

сферической систем координат.

Рекомендуемая литература.

1. Рашевский П.К. Курс дифференциальной геометрии. М., ГИТТЛ, 1956.

2. Шутц Б. Геометрические методы теоретической физики. М., МИР, 1984.

3. Ландау Л.Д., Лифшиц Е.М. Механика. М., НАУКА, 1988.

4. Павленко Ю.Г. Задачи по теоретической механике. М., МГУ, 1988.

-46-

С первой половины 17-го века, когда Рене Декарт впервые ввел координаты (получившие название декартовых) для определения точек пространства, системы координат получили широкое применение в физике и математике. Они позволили использовать мощные аналитические методы для выражения законов физических явлений и их исследования. Более того, оказалось, что координатные методы несут в себе огромный эвристический заряд. Трудно представить себе без координатных методов появление таких разделов науки, как аналитическая геометрия, риманова геометрия и многих других в математике, или лагранжева механика, электродинамика и других физических теорий. Координатные методы являются основным инструментом и в теоретической механике. Приведем для примера, помимо декартовых координат, координаты сферические, цилиндрические, эллиптические для реального 3-х мерного пространства, или обобщенные координаты в конфигурационном и фазовом пространствах механической системы.

1. – мерное векторное пространство

Определение 1. Пусть векторы принадлежат множеству . Множество называется векторным пространством, если на нем определены бинарная операция, обозначаемая знаком “ + “, и операция умножения элементов множества на действительные числа обозначаемая символом “ “, удовлетворяющие следующим аксиомам:

-3-

1. ;

2. ;

3. ;

4. Имеется нуль-вектор

такой, что

,

;

5. ;

6. ;

7. ;

8. ;

9. , .

Аксиома 1 является определением суммы двух векторов, обладающей свойством ассоциативности (аксиома 2) и симметрии относительно перестановки слагаемых векторов (аксиома 3). Аксиома 5 определяет умножение векторов на действительные числа, обладающее свойством ассоциативности (аксиомы 6 8).

Определение 2. Векторы называются линейно независимыми, если равенство

(1.1)

выполняется тогда и только тогда, когда

-4-

Поэтому

Подставляя полученные значения и в (6.19), находим искомую формулу для угловой скорости вращения подвижного базиса Френе

(6.20)

Из этой формулы следует еще один геометрический смысл кривизны и кручения кривой: кривизна равна угловой скорости вращения подвижного базиса в соприкасающейся плоскости , направление вращения всегда совпадает с бинормалью ; кручение кривой также равно угловой скорости вращения, но уже в нормальной плоскости , а направление вращения параллельно вектору и зависит от знака .

Упражнения.

1. Докажите, что множество ортогональных

матриц образуют группу. Ее принято обозначать

2. Докажите, что множество унимодулярных

ортогональных матриц образуют группу.

Эту группу обозначают как . Покажите,

-45-

базисов , с которыми ассоциированы базисы . Вектор угловой скорости базисов является также вектором угловой скорости вращения координатных базисов, с которыми они ассоциированы.

Замечание. Следует помнить, что правая часть формулы (6.18) является только частью, а именно ротационной, полной производной по , если вектор не является постоянным во вращающемся координатном базисе.

Пример. Найдем угловую скорость подвижного базиса Френе. Представим для этого искомый вектор его компонентами в базисе Френе

(6.19)

Применим формулу (6.18) к вектору и воспользуемся уравнением (5.12 b) Френе. Получим

Отсюда следует, что

Теперь применим формулу (6.18) к вектору и воспользуемся уравнением Френе (5.12 d). Имеем

-44-

Определение 3. Максимальное число линейно независимых векторов называется размерностью векторного пространства.

Следствие 1. Если – размерность векторного пространства, то для любых векторов существуют не равные нулю числа такие, что

. (1.2)

Следствие 2. Если векторов являются линейно независимыми, то любой вектор может быть представлен в виде

, (1.3)

где хотя бы одно из чисел не равно нулю. В этом случае говорят, что равенство (1.3)

представляет собой “разложение” вектора по линейно независим векторам .

Следствие 3. Если существует один набор линейно независимых векторов, то существует неограниченное множество наборов из линейно независимых векторов.

Примеры векторных пространств

1. Множество всех “обычных” векторов, определяемых в трехмерном евклидовом пространстве посредством длины вектора и его направления.

-5-

2. Множество всех вещественных матриц типа . Размерность такого пространства равна .

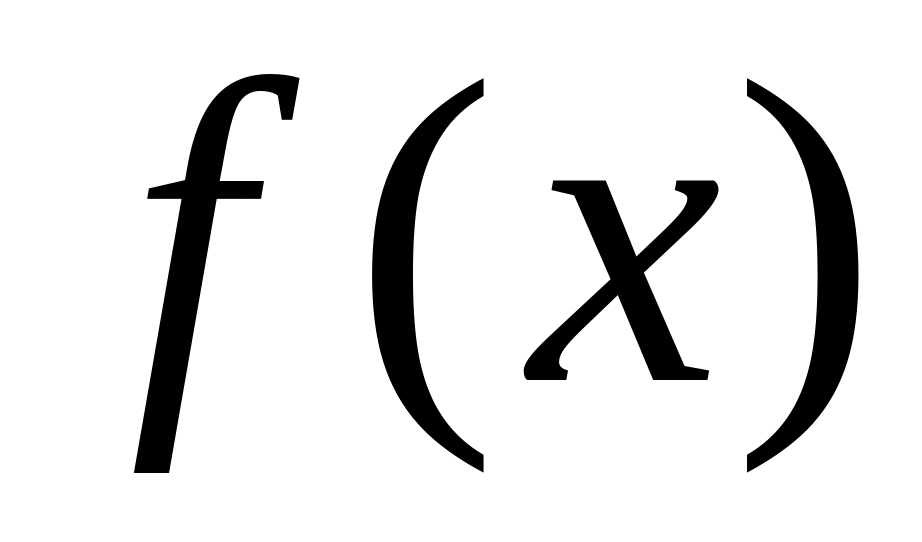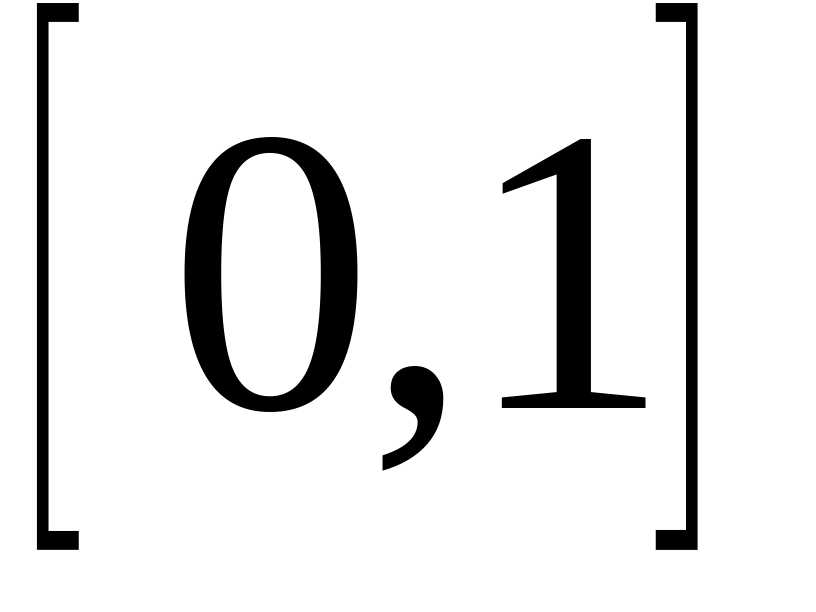3. Множество всех вещественных непрерывных функций , определенных на интервале , бесконечномерное пространство.

Упражнение.

Показать, что множества, указанные в примерах 2 и 3 , удовлетворяют всем аксиомам векторного пространства.