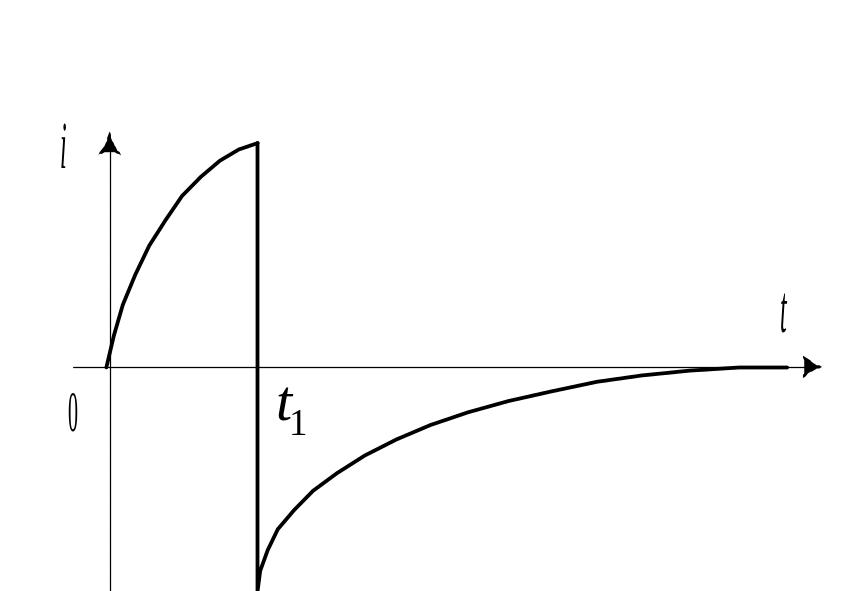10.4. Переходные процессы при воздействии одиночных импульсов

Большой класс радиотехнических и вообще электротехнических задач связан с исследованием процессов в электрических цепях, протекающих под воздействием кратковременных внешних возмущений, длительность которых сравнима с длительностью переходных процессов. Такие возмущения будем называть импульсными. Импульсными системами будем считать устройства, в которых формируются и действуют импульсные э.д.с. и токи.

Передача и преобразование сигналов при помощи импульсов находят широкое применение для передачи информации, так как при этом влияние помех оказывается наименьшим. Благодаря кратковременности импульсного процесса появляется возможность получать импульсы весьма большой мощности, в сотни раз превышающей мощность соответствующего устройства при непрерывной его работе. Весьма широко используется импульсный метод в автоматике, телемеханике, радиотехнике и т.д.

Для исследования импульсных процессов применимы классический и операторный методы расчета переходных процессов. При определенных формах импульсов и характере изменения интервалов между ними возможны различные специальные методы анализа процессов в импульсных системах. Одним из них в случае следования импульсов друг за другом через равные промежутки времени является метод разностных уравнений, решение которых основывается на дискретном преобразовании Лапласа.

Изучение импульсных цепей начнем с уже знакомых методов анализа переходных процессов: классического и операторного.

10.4.1. Классический метод анализа

Пример 10.6

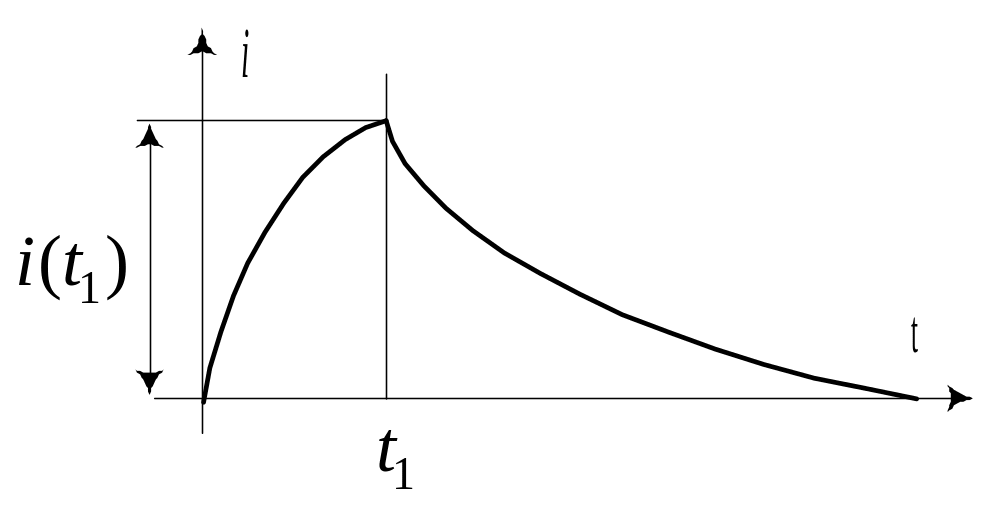
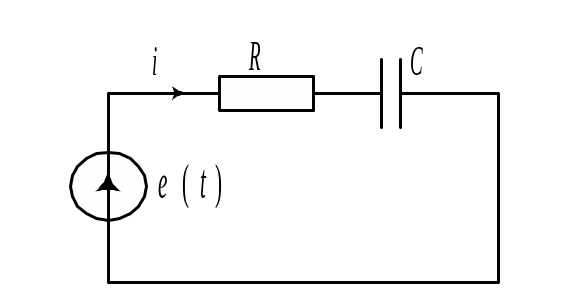
Рассчитать ток в цепи (рис. 10.14,а) при воздействии на него прямоугольного импульса напряжения (рис. 10.14,б).

а)		б)
Рис. 10.14

Решение

Запишем дифференциальное уравнение цепи по второму закону Кирхгофа:

, где . (10.6)

Для интервала времени дифференциальное уравнение (10.6) примет вид

. (10.7)

Решение уравнения (10.7) было ранее получено в главе 9:

, (10.8)

где – постоянная времени цепи.

Рассмотрим теперь интервал времени . На этом интервале уравнение (10.6) имеет вид

. (10.9)

Решение однородного дифференциального уравнения (10.9):

. (10.10)

Постоянную интегрирования B определим из закона коммутации для тока катушки индуктивности , тогда при из уравнений (10.8) и (10.10) получим

. (10.11)

Итак, на интервале времени ток в цепи

. (10.12)

Временная зависимость тока в рассматриваемой цепи показана графически на рис. 10.15. В интервале времени ток в катушке воз-

растает от нуля до . Следовательно, энергия магнитного поля катушки изменится от нуля до .
	Рис. 10.15

Далее при переходный процесс в цепи обусловлен запасом энергии, накопленной в магнитном поле индуктивности.

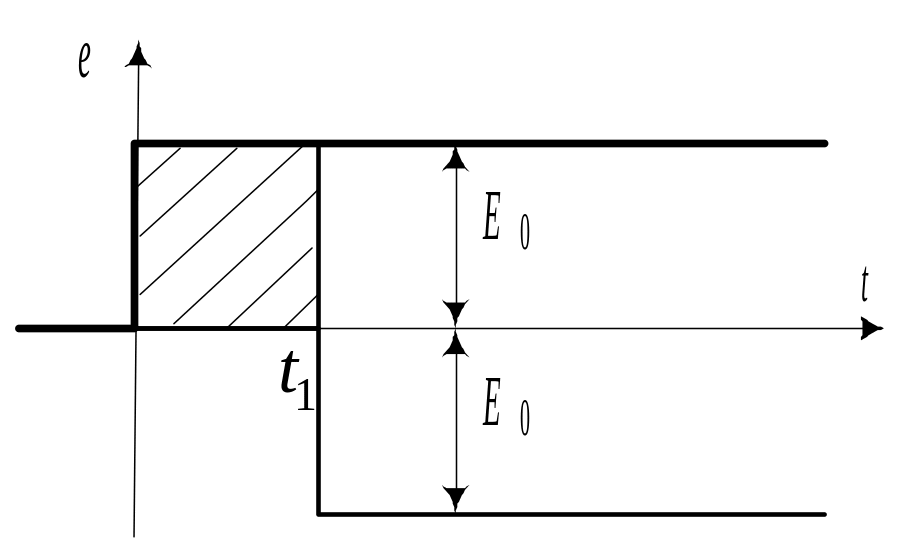
В заключение отметим, что данная задача легко может быть решена с помощью принципа наложения. Прямоугольный импульс продолжительностью может быть представлен в виде суммы двух постоянных э.д.с., одна из которых (положительная) подключается к цепи в момент времени t = 0, а другая (отрицательная) – при .
	Рис. 10.16

Изобразим эти э.д.с. на графике (рис. 10.16).

Реакция цепи на каждую из постоянных э.д.с. известна. Ток в цепи при включении ее на постоянную э.д.с. при уже был получен (10.8). Ток в цепи при включении ее на постоянную э.д.с. противоположного знака при получается из (10.8) в виде

. (10.13)

В соотношении (10.13) знак “минус” учитывает направление э.д.с., сдвиг по времени в показателе экспоненты учитывает, что э.д.с. подключается к цепи спустя время .

Теперь, используя принцип наложения, находим реакцию на прямоугольный импульс. В интервале времени действует только одна э.д.с. и, следовательно, ток определяется соотношением (10.8). При в цепи действует оба источника, поэтому ток в цепи равен сумме выражений (10.8) и (10.13):

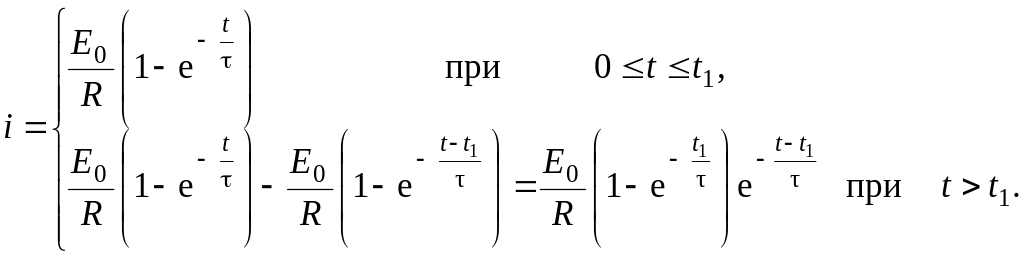(10.14)

Решение (10.14) полностью соответствует выражениям (10.8) и (10.12), причем в случае прямоугольного импульса рассматриваемый метод оказался несколько проще. Однако, для отыскания реакции на импульс более сложной формы целесообразным представляется общий подход, рассмотренный выше.

Пример 10.7

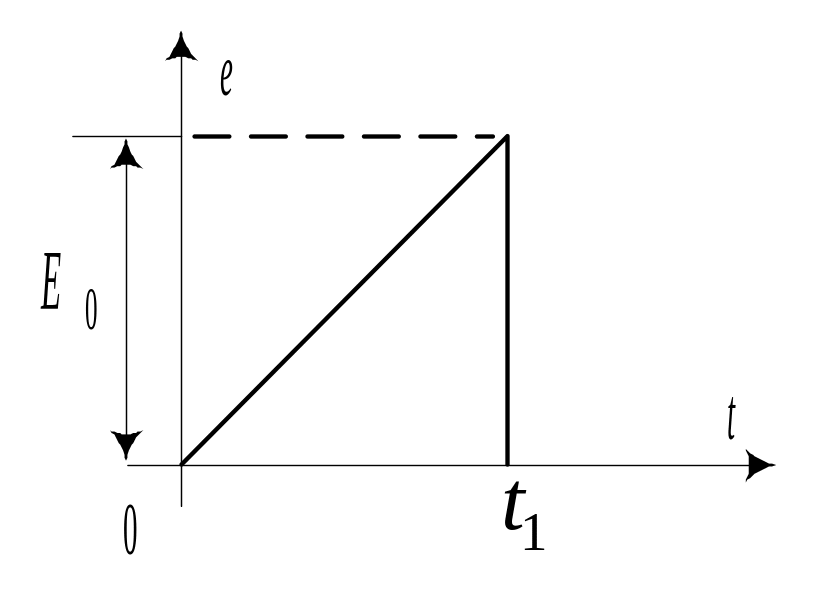
Рассчитать напряжения на элементах цепи (рис. 10.17,а) при воздействии на неё треугольного импульса напряжения (рис. 10.17,б).

а)		б)
Рис. 10.17

Решение

Дифференциальное уравнение для цепи имеет вид

, где (10.15)

Как и в предыдущем примере, решение уравнения (10.15) будем искать отдельно на двух интервалах времени и . На первом интервале уравнение (10.15) перепишется следующим образом

. (10.16)

Решение неоднородного дифференциального уравнения (10.16) складывается из частного решения неоднородного дифференциального уравнения и общего решения однородного дифференциального уравнения. Частное решение неоднородного дифференциального уравнения ищем в виде где А и В – постоянные интегрирования. Определяем их подстановкой частного решения в дифференциальное уравнение (10.16):

откуда ; , где – электромагнитная постоянная времени цепи. С учетом найденных значений постоянных интегрирования частное решение уравнения (10.16) примет вид

(10.17)

Общее решение однородного дифференциального уравнения:

(10.18)

Постоянную интегрирования находим из начальных условий, которые в свою очередь определяем из закона коммутации . Следовательно, при общее решение дифференциального уравнения (10.16) имеет вид

откуда . В результате получаем полное решение неоднородного дифференциального уравнения (10.16):

(10.19)

При уравнение (10.15) запишется следующим образом:

(10.20)

Решение однородного дифференциального уравнения (10.20) имеет вид

. (10.21)

Постоянную интегрирования находим из закона коммутации для напряжения на ёмкости . Таким образом, при из уравнений (10.19) и (10.21) получаем:

,

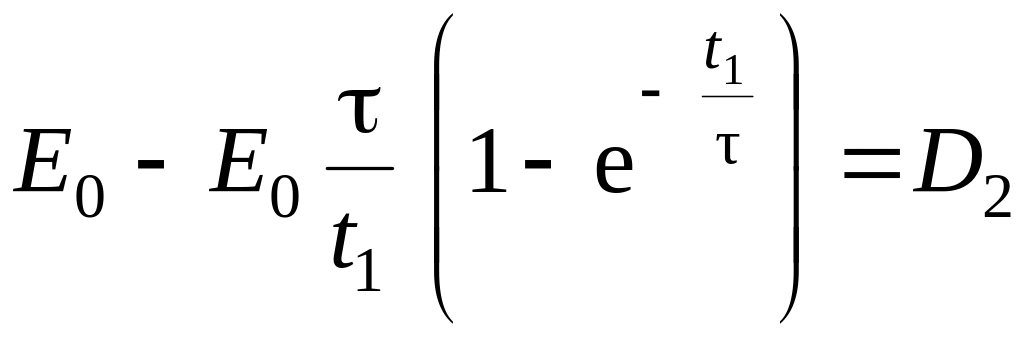тогда решение уравнения (10.20) примет вид

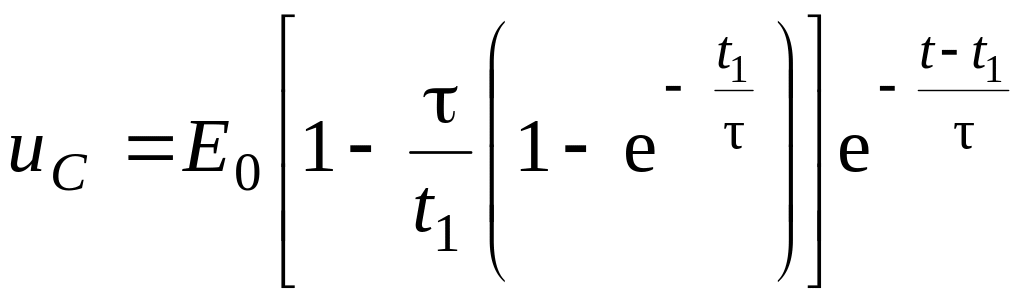. (10.22)

Напряжение на резисторе вычислим по формуле и для интервала времени получаем:

.

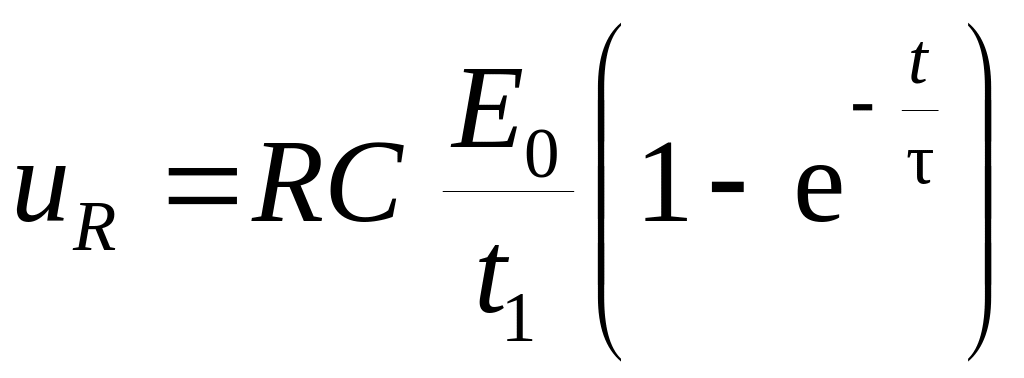Для интервала времени напряжение на резисторе

.

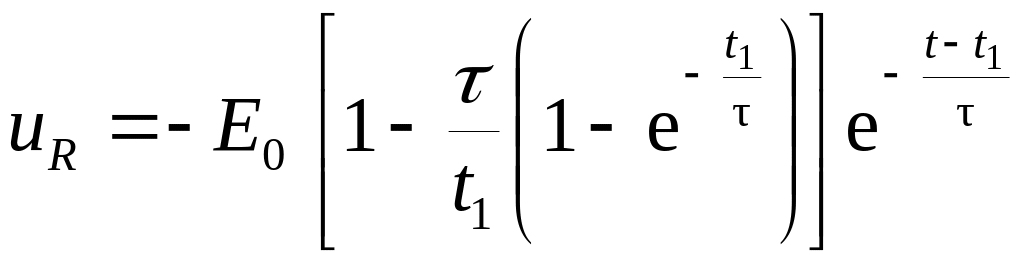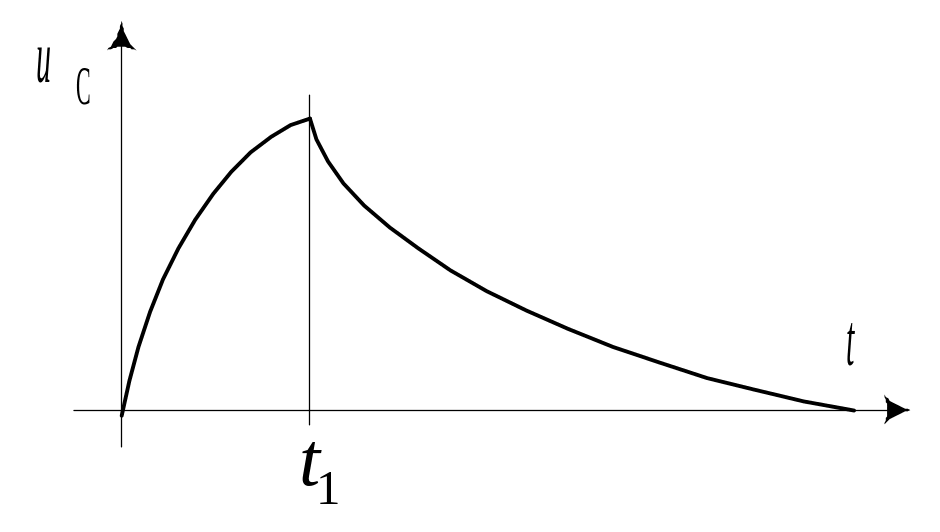
Графики изменения напряжений на конденсаторе и резисторе приведены на рис. 10.18. За время действия импульса происходит накопление энергии в электрическом поле конденсатора. Переходный процесс в цепи после окончания импульса обусловлен запасом энергии, накопленной конденсатором.

а)		б)
Рис. 10.18

Теперь рассмотрим два частных случая:

1. электромагнитная постоянная времени много больше длительности импульса ;

2. электромагнитная постоянная времени много меньше длительности импульса .

В первом случае напряжение на конденсаторе

.

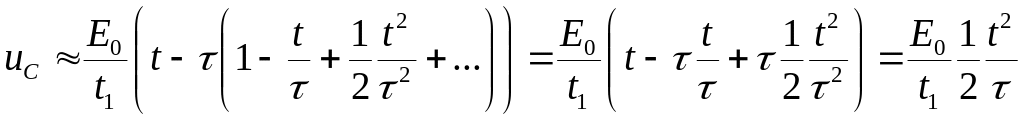Легко убедиться, что напряжение пропорционально интегралу от входного сигнала

,

т. е. при рассматриваемых условиях цепь является интегрирующей. После окончания импульса это свойство цепи не исчезает, поскольку для отключения импульса также выполняется условие .

Во втором случае напряжение на резисторе

.

Легко убедиться, что напряжение пропорционально производной входного сигнала

,

т. е. в рассматриваемых условиях цепь является дифференцирующей. После окончания импульса «дифференцирующее» свойство цепи исчезает, поскольку импульс отключается мгновенно и для времени отключения не выполняется условие .

Пример 10.8

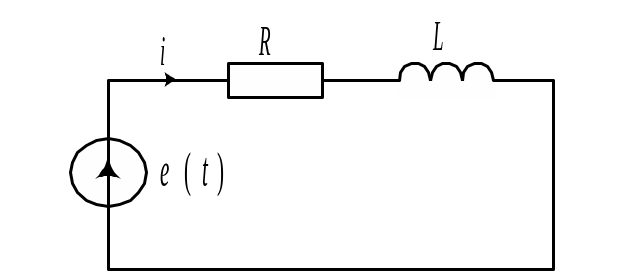
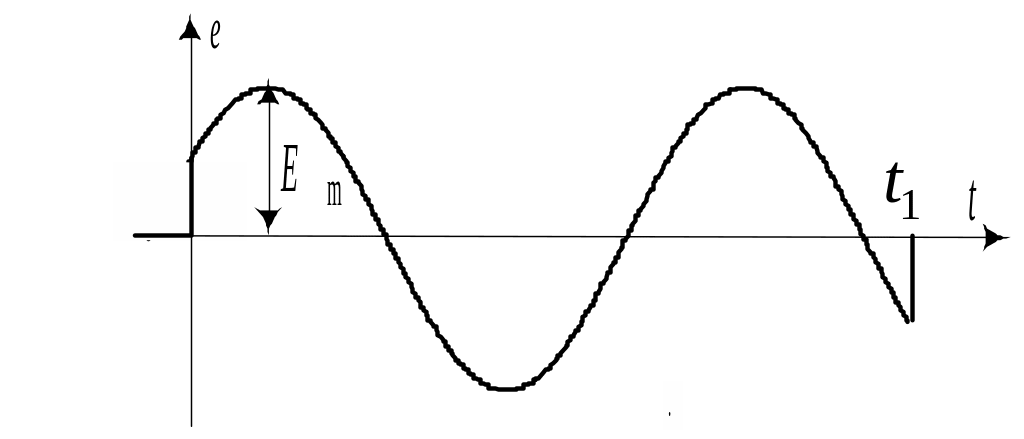
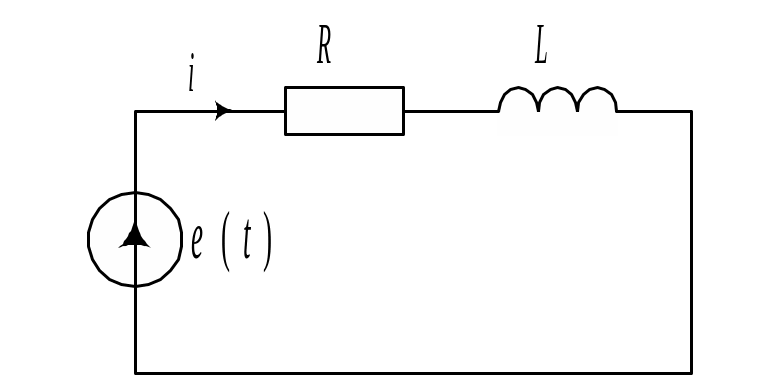
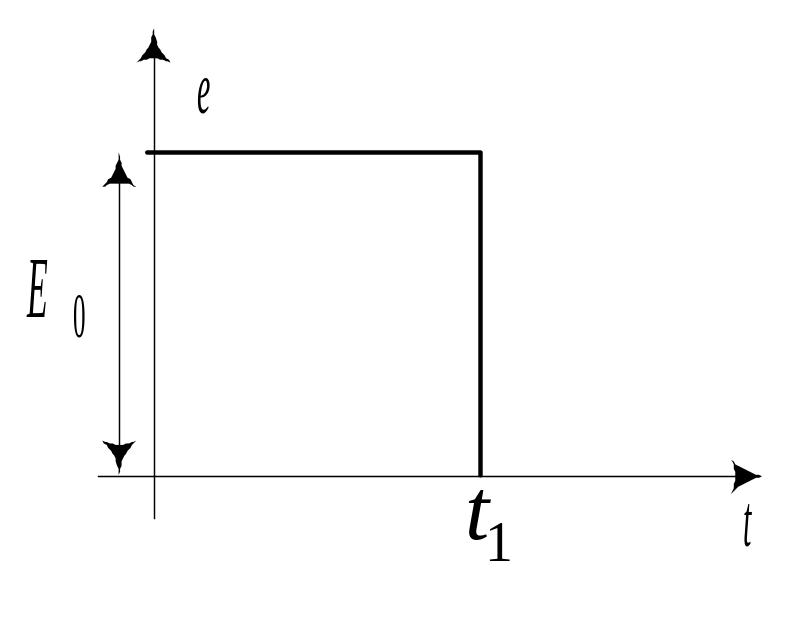
Рассчитать ток в цепи (рис 10.19,а) при воздействии импульса гармонических колебаний с прямоугольной огибающей (рис. 10.19,б).

а)	б)
Рис. 10.19

Решение

Дифференциальное уравнение для данной цепи, составленное по второму закону Кирхгофа, имеет вид

, где .

Задача по-прежнему сводится к решению дифференциального уравнения, составленного для данной цепи на двух интервалах времени и _.

На интервале процессы в рассматриваемой цепи определяются уравнением

(10.23)

Решение неоднородного дифференциального уравнения (10.23) было получено в п. 9.3.3 и имеет вид

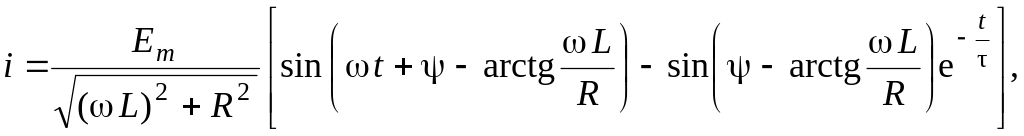(10.24)

где – электромагнитная постоянная времени. Напряжение на катушке индуктивности в этом же интервале времени:

.

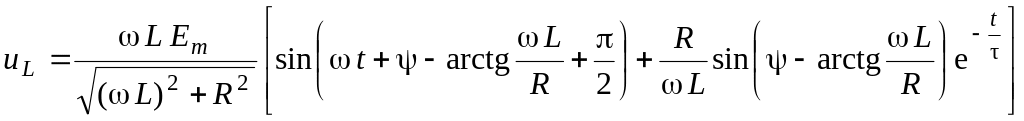После окончания импульса в цепи возникает переходный процесс, обусловленный запасом энергии магнитного поля катушки индуктивности и описываемый уравнением

.

Решение этого уравнения имеет вид

(10.25)

Постоянную интегрирования В определяем из закона коммутации для тока через катушку индуктивности: . Приравнивая выражения (10.24) и (10.25) при , получаем:

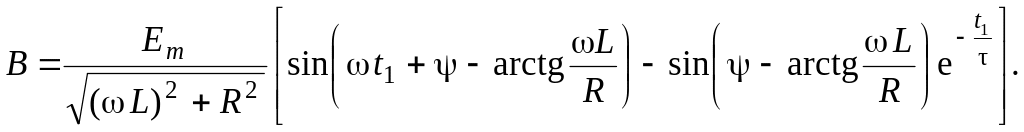
Учитывая постоянную интегрирования, записыванием закон изменения тока для интервала времени :

.

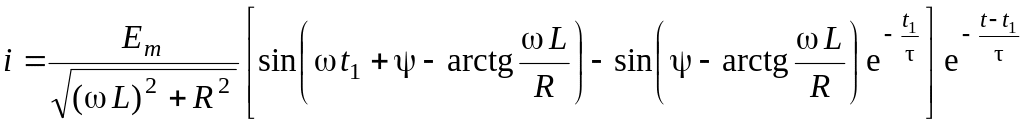Напряжение на катушке индуктивности

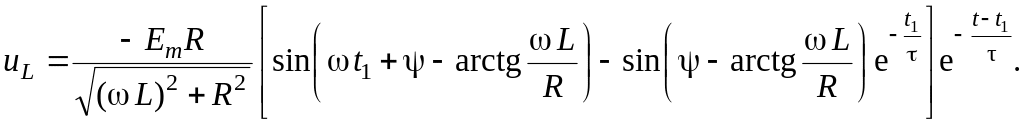
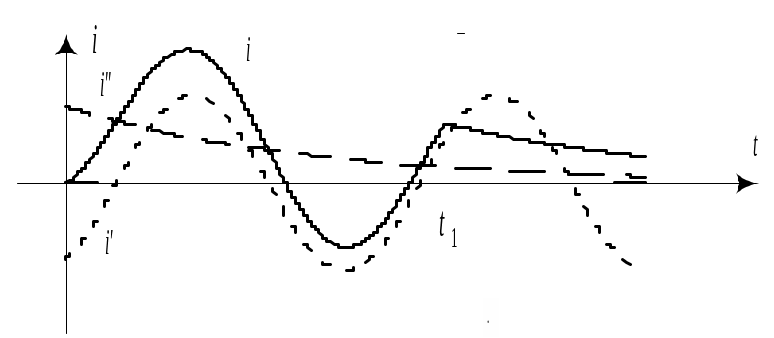
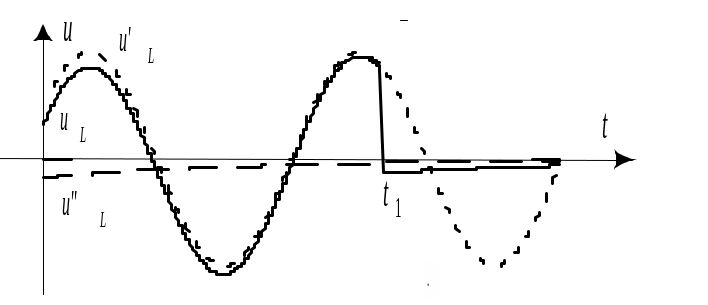
Графики изменения тока в цепи и напряжения на индуктивности приведены на рис. 10.20.

а)	б)
Рис. 10.20

В момент времени скачок напряжения на индуктивности составит

что соответствует скачку э.д.с. в цепи в момент окончания импульса.

В заключение, сформулируем некоторые закономерности классического метода расчета реакции цепи на одиночный импульс.

Расчет переходного процесса сводится к нахождению двух различных законов изменения тока в цепи на интервале времени действия импульса э.д.с. и после окончания импульса.

На интервале действия импульса ток переходного процесса находится в виде суммы двух токов. Первый ток является частным решением неоднородного дифференциального уравнения, определяемым правой частью этого уравнения. В частном случае, когда правая часть уравнения является постоянной или синусоидальной функцией времени, ток может быть найден с использованием методов расчета цепей постоянного и ли синусоидального тока. Второй ток является общим решением однородного дифференциального уравнения, составленного для свободной составляющей тока в рассматриваемой цепи.

После окончания импульса переходный процесс в цепи происходит за счет запаса энергии магнитного поля индуктивности или электрического поля ёмкости. Этот процесс описывается однородным дифференциальным уравнением.

Постоянные интегрирования на обоих интервалах определяем из законов коммутации в момент включения импульса и в момент его окончания.