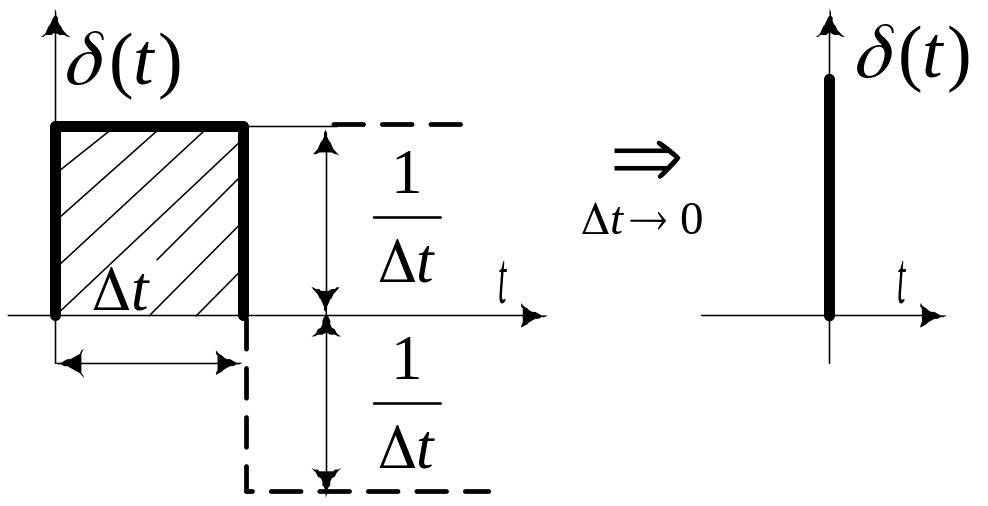Глава 10

ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ ИМПУЛЬСНЫХ

ВОЗДЕЙСТВИЯХ И Э.Д.С. СЛОЖНОЙ ФОРМЫ

10.1. Переходные процессы в электрической цепи

при воздействии э.д.с. сложной формы

10.1.1. Общая характеристика переходных процессов

при воздействиях сложной формы

В задачах связи, автоматики, телемеханики и радиоэлектроники возникает необходимость в определении реакции на воздействия, имеющие разнообразные сложные формы, а также содержащие точки разрыва и излома. Применение классического и операторного методов анализа переходных процессов в этом случае не всегда эффективно. Особенно это проявляется, если внешнее воздействие имеет точки разрыва и излома. Тогда необходимо проводить расчет на отдельных участках возмущений и стыковать решения на участках на основе законов коммутации. В операторном методе нахождение оригинала по изображению также может представлять сложную математическую задачу, поскольку в изображениях по Лапласу могут появиться полиномы с большим или даже бесконечно большим числом полюсов.

Чтобы избавиться от указанных недостатков, целесообразно применять принцип наложения. Идея метода заключается в том, чтобы функцию внешнего воздействия представить в виде суммы простых аналитически однотипных функций

.

Если реакция цепи на воздействие известна, то на основании принципа наложения можно утверждать, что искомая реакция при воздействии является суммой реакций

.

Очевидно, что функция при заданном воздействии будет зависеть только от структуры и параметров цепи. Поэтому можно рассматривать, как некоторую временную характеристику исследуемой цепи. Практически эта характеристика может быть определена из решения соответствующего дифференциального уравнения или опытным путем.

Систему функций необходимо выбрать так, чтобы можно было входное возмущение представить в виде аналитического выражения, и расчет реакций цепи был простым. В качестве аналитически однотипных функций используются так называемые единичные, импульсные и синусоидальные функции.

10.1.2. Единичная и импульсная функции.

Обобщенное дифференцирование сигнала

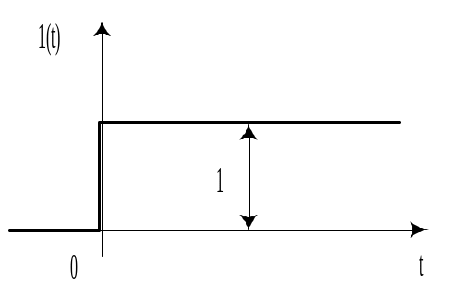
При расчете переходных процессов в электрических цепях в качестве типовых возмущений используют единичную функцию (функцию Хевисайда) и -функцию (функцию Дирака). Функция Хевисайда (рис. 10.1) определяется как (10.1)
	Рис. 10.1

Также используют функции Хевисайда от смещенного и от отрицательного аргументов:

Для функций Хевисайда выполняются следующие очевидные соотношения: ; .

С помощью единичной функции (10.1) можно аналитически описать подключение цепи к источнику. Например, если электрическая цепь в момент времени включается на постоянное напряжение , то . Если воздействие подается на цепь не в момент времени , а с запаздыванием на время , его также можно записать с помощью смещенной единичной функции .

С помощью единичной функции (10.1) можно аналитически записать любую разрывную функцию, так функцию

с использованием единичной функции можно записать в виде

.

С помощью единичных функций можно записать импульс в виде .

Для введения дельта-фунции , рассмотрим предварительно прямоугольный импульс длительностью и величиной (рис. 10.2). Этот импульс можно представить аналитически как Если в этом выра-
	Рис. 10.2

жении устремить к нулю, то в пределе получим -функцию или функцию Дирака

(10.2)

Функция Дирака обладает следующими свойствами.

1. Из определения следует, что

2. Интеграл от -функции

3. -функцию можно рассматривать как производную от единичной функции: .

4. -функция, смещенная на время , имеет вид

;

5. -функция обладает фильтрующим действием, т.е. при умножении некоторой функции на функция сохраняет свое значение только в момент времени :

;

6. Интеграл от произведения функции на -функцию :

.

Использование единичных или дельта функций (10.1), (10.2) позволяет записать функции, имеющие разрывный или импульсный характер, единым выражением в виде обобщенных функций. Такой математический аппарат обобщенных функций дает возможность дифференцировать функции, которые с точки зрения классического анализа являются не дифференцируемыми.

Пусть функция задана в виде двух непрерывных функций и , имеющих разрыв при ,

При обычном классическом рассмотрении производная будет определена во всех точках существования непрерывных функций и , кроме точки разрыва .

Обобщенная производная функции имеет вид

Если непрерывна в точке , то и обобщенная производная совпадает с обычной: . Для функции , имеющей разрыв, можно получить обобщенные производные любого порядка

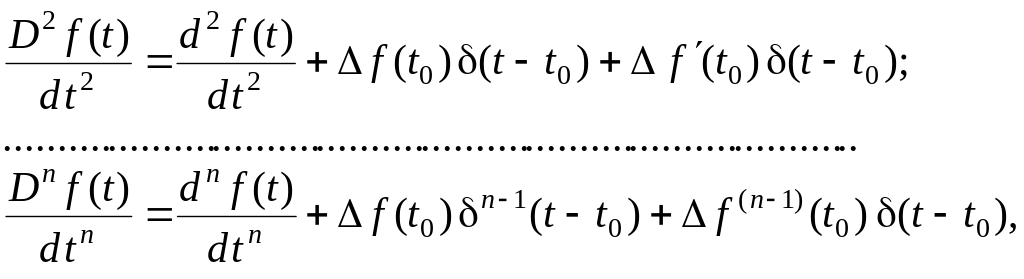
где – разрыв функции в точке ; -я производная от -функции.

Если функция имеет несколько точек разрыва , то обобщенная производная функции вычисляется аналогично для каждой точки разрыва:

.

Для иллюстрации изложенного рассмотрим пример.

Пример 10.1

Для функции

(рис. 10.3) найти первую и вторую обобщенные производные.
	Рис. 10.3

Решение

Обычная производная функции имеет разрыв при , причем разрыв функции , тогда, Далее, имеем: . Следовательно, вторая обобщенная производная функции .