
- •Тема I – линейная алгебра
- •1. Матрицы и определители Задания для подготовки к практическому занятию
- •Задания к практическому занятию
- •Задания для подготовки к практическому занятию
- •Вопросы и задачи
- •Задания к практическим занятиям
- •Тема II – аналитическая геометрия
- •Задания для подготовки к практическому занятию
- •Вопросы и задачи
- •Задания к практическому занятию
- •Задания для подготовки к практическому занятию
- •Вопросы и задачи
- •Задания к практическому занятию
- •Тема III – основы математического анализа
- •8. Предел последовательности Задания для подготовки к практическому занятию
- •Вопросы и задачи
- •Задачи к практическому занятию
- •Задания для подготовки к практическому занятию
- •Вопросы и задачи
- •Задачи к практическому занятию
- •11. Производная функции Задания для подготовки к практическому занятию
- •1. Дифференциал функции
- •2. Производные и дифференциалы высших порядков
- •14. Функции нескольких переменных Задания для подготовки к практическому занятию
- •Задачи к практическому занятию
Задания к практическому занятию
1. Вычислить существующие произведения матриц из задания п6
2. Выполнить действия, если это возможно:
а) А3,
где
 ;
б)2А2+3А+5Е,
где
;
б)2А2+3А+5Е,
где
 ;
;
в) А+В; А+ВТ;
АТ+В;
АВ; ВА, где
 ;
;
3. Вычислить определители:
а)
 ;
б)
;
б)
 ;
в)
;
в) ;
г)
;
г)
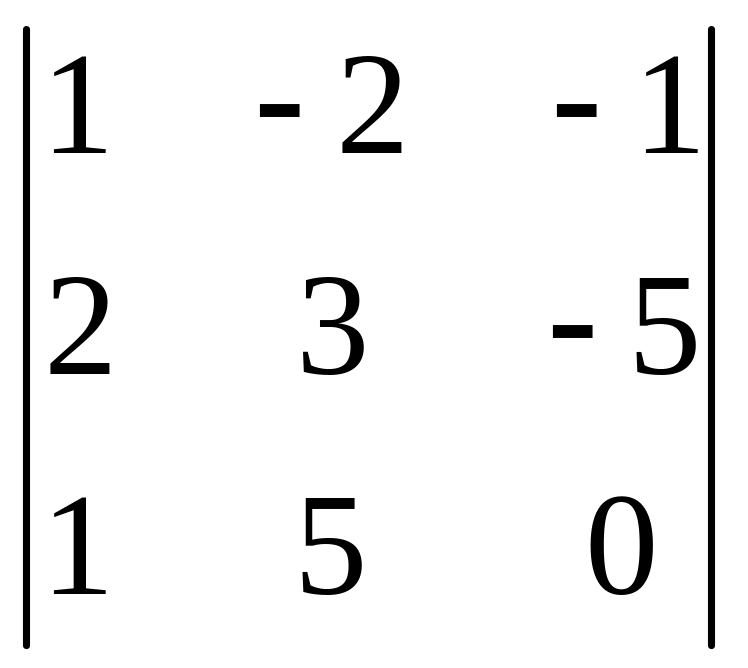 ;
;
д)
 ;
е)
;
е)
 ;
ж)
;
ж)

4. Вычислить определитель. При каком значении параметра он равен 0?
а)
 ;
б)
;
б)

2-3. Обратная матрица. Матричные уравнения. Системы линейных алгебраических уравнений.
Задания для подготовки к практическому занятию
Прочитайте §3,4 лекций и предложенные примеры. Ответьте письменно на вопросы и решите задачи.
Примеры.
Даны матрицы:

1. Существуют ли обратные для данных матриц? Если да, найдите и выполните проверку.
Решение:
Матрица А
квадратная, ее определитель равен
![]() ,
следовательно, А-1
существует. Матрица В
квадратная, но ее определитель
,
следовательно, А-1
существует. Матрица В
квадратная, но ее определитель
![]() ,
следовательно, В-1
не существует. Матрица С
размера 32,
не квадратная, следовательно, С-1
не существует.
,
следовательно, В-1
не существует. Матрица С
размера 32,
не квадратная, следовательно, С-1
не существует.
Найдем обратную матрицу для матрицы А. Прежде всего, транспонируем матрицу А:
 .
.
Составим присоединенную матрицу из алгебраических дополнений к элементам матрицы АТ:

Вычислим обратную матрицу по формуле
 .
.
Проверим: произведение матрицы и ее обратной должно быть единичной матрицей
 ,
,
что и требовалось доказать, т.е. матрица А-1 найдена верно.
Замечание:
удобнее перемножать целочисленные
матрицы, поэтому мы сначала перемножили
матрицы
![]() и А,
а результат домножили на дробь. Этим
приемом мы будем пользоваться и далее.
и А,
а результат домножили на дробь. Этим
приемом мы будем пользоваться и далее.
2. Решить матричные уравнения АХ=В и YА=В.
Решение: Уравнение АХ=В, если матрица А имеет обратную, решается по формуле Х=А-1В. Получаем:

Уравнение YА=В,
если матрица А
имеет обратную, решается по формуле
Y=ВА-1.
Получаем:

3. Записать систему
линейных уравнений в виде матричного
уравнения: 
Решение: Система линейных уравнений эквивалентна матричному уравнению АХ=В, где Х – столбец неизвестных; А – матрица коэффициентов при неизвестных в левых частях уравнений (необходимо следить за очередностью неизвестных в записи уравнения; если неизвестной в уравнении нет, значит, соответствующий коэффициент равен 0); В – столбец свободных коэффициентов:
 ;
;
 ;
;

4. Решить систему из п3 при помощи правила Крамера
Решение: Прежде всего, найдем определитель системы:
 ,
,
следовательно,
система имеет единственное решение,
которое можно найти по правилу Крамера.
Для определения значения переменной х
вычислим определитель
![]() ,
полученный из
заменой столбца коэффициентов при
переменной х
на столбец свободных коэффициентов:
,
полученный из
заменой столбца коэффициентов при
переменной х
на столбец свободных коэффициентов:
 ,
значит,
,
значит,
![]() .
.
Аналогично,
определитель
![]() получаем из
заменой столбца коэффициентов при
переменной y
на столбец свободных коэффициентов:
получаем из
заменой столбца коэффициентов при
переменной y
на столбец свободных коэффициентов:
 ,
,
![]() .
.
Далее, определитель
![]() получаем из
заменой третьего столбца на столбец
свободных коэффициентов:
получаем из
заменой третьего столбца на столбец
свободных коэффициентов:
 ,
,
![]()
Таким образом, решением системы является тройка чисел (-1;1;1). Подстановкой в уравнения системы убеждаемся, что решение найдено верно.
Вопросы и задачи
п1. Существуют ли обратные матрицы для матриц
 ,
,
 ,
,
 ?
?
п2. Проверьте, является ли А-1 обратной матрицей для матрицы А:
а) ,
, ;
б)
;
б)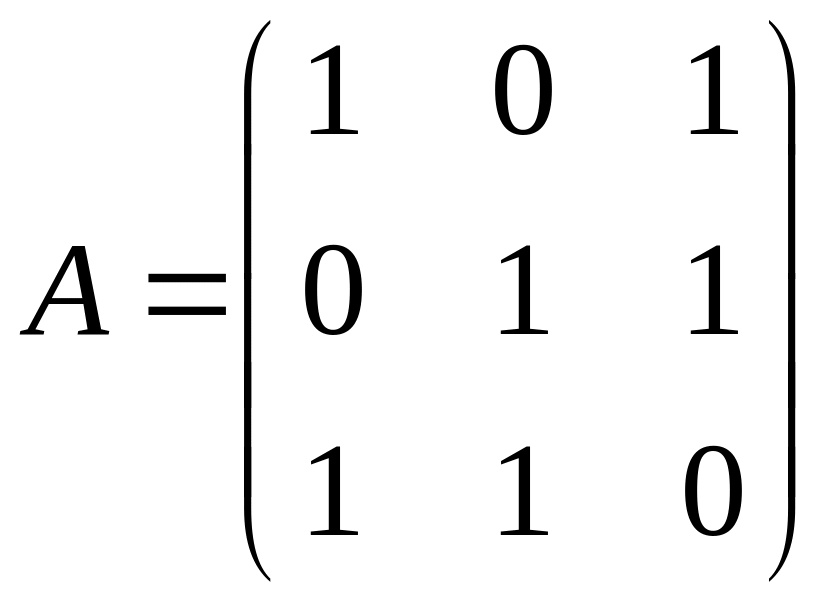 ,
,
п3. Найдите обратную матрицу для матрицы . Проверьте результат.
п4. Решите матричные уравнения: а) АХ=В; б) ХА=В,
если
,

п5. Запишите систему линейных уравнений в виде матричного уравнения:
а)
 ;
б)
;
б)

п6. Решите систему а) из предыдущего задания при помощи обратной матрицы
п7. Решите, используя правило Крамера:
а)
 ;
б)
;
б)

п8. Можете ли вы привести пример системы линейных уравнений, которая имела бы ровно 2 решения?
