Свойства определенного интеграла
Пусть все рассматриваемые функции являются непрерывными, так что определенные интегралы от них существуют. Тогда справедливы следующие соотношения:
1.
2.
3.
4.
5.
6. Если
.
Если функции
непрерывна на отрезке
и
-
какая-нибудь первообразная для
на этом отрезке, то справедлива формула
Ньютона-Лейбница:
.
Правую часть формулы часто обозначают
символом
(знак двойной подстановки от
до
).
Пример1.
Вычислить определенный интеграл
.
Решение.
.
Замена переменной в определенном интеграле
Пусть функция
непрерывна на отрезке
,
а функция
определена и непрерывна вместе со своей
производной
на отрезке
,
причем
для любого
и
,
Тогда:
Эта формула называется формулой замены переменной в определенном интеграле или формулой интегрирования подстановкой.
Пример2.
Вычислить определенный интеграл
.
Решение.
Сделаем замену переменной
.
Тогда
.
Пересчитаем пределы интегрирования:
при
,
а при
.
.
Заметим, что при вычислении определенного интеграла к старой переменной не возвращаются.
Интегрирование по частям в определенном интеграле
Теорема. Если функции
и
дифференцируемы на отрезке
,
то справедлива следующая формула
.
Пример3.
Вычислить
.
Решение.
Обозначим
,
.
Тогда
,
.
.
Геометрические приложения определенного интеграла Площадь плоской фигуры
Площадь
криволинейной трапеции, ограниченной
графиком
,
осью
и прямыми
и
(рис.2) вычисляется по следующей формуле:
Если
часть кривой
находится под осью
(рис.3), то площадь заштрихованной фигуры
равна:
.
Пусть фигура ограничена двумя кривыми
,
и
,
(рис. 4). Тогда ее площадь вычисляется
по формуле
.
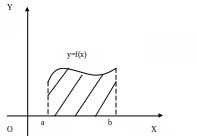
Рис.2
Рис. 3
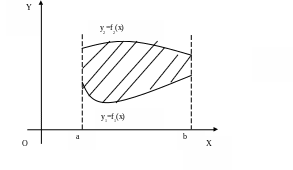
Рис. 4
Пример4.
Вычислить площадь фигуры, ограниченной
прямой
и параболой
.
Решение. Построим графики прямой и параболы
(рис. 5).
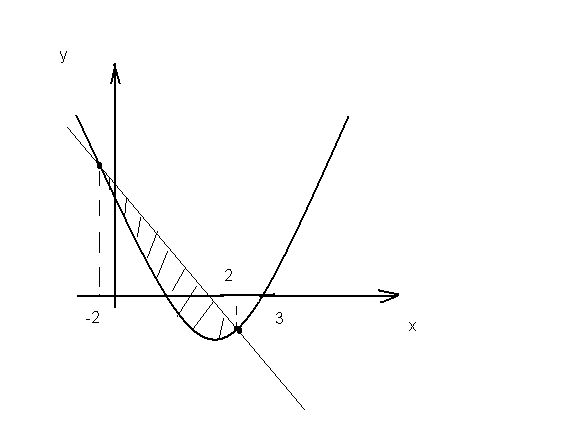
Рис. 5.
Найдем точки пересечения параболы и прямой:
.
Тогда получим:
.
Объем тела вращения
Пусть функция непрерывна на отрезке . В этом случае объем тела, образованного вращением вокруг оси криволинейной трапеции, ограниченной графиком функции , прямыми , и осью , вычисляется по формуле:
.
Если
тело получено вращением кривой
вокруг оси
,
то объем этого тела вычисляется по
формуле:
.
Пример5.
Вычислить объем тела, образованного
вращением фигуры, ограниченной линиями
вокруг оси
.
Решение. На рис.6 показана фигура, образующая тело вращения.
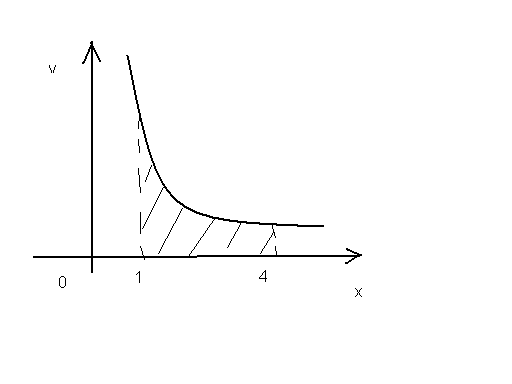
Рис. 6
.
Контрольные задания
Вычислить площадь фигуры, ограниченной линиями (2.1-2.10) .
Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций, вокруг оси OX (2.11-2.15).
Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций вокруг оси OY (2.16-2.20).
6.1.
;
.
6.2.
;
.
6.3.
;
;
.
6.4.
;
;
;
.
6.5.
;
;
.
6.6.
;
.
6.7.
;
.
6.8.
6.9.
6.10.
6.11.
;
.
6.12.
;
.
6.13.
;
.
6.14.
6.15.
.
6.16.
;
.
6.17.
;
,
.
6.18.
;
,
.
6.19.
6.20.
