Примеры решения задач

Задача 3.1. Найти момент инерции прямоугольного однородного тела, со сторонами, равными а, b, c ( ) и плотностью относительно осей 00' и 0''0'''.

На расстоянии x от оси 00' выделим полоску шириной dx (рис. 3.1), масса которой равна . По определению момент инерции тела относительно оси 00' .

С учётом запишем тогда момент инерции заданного тела

.

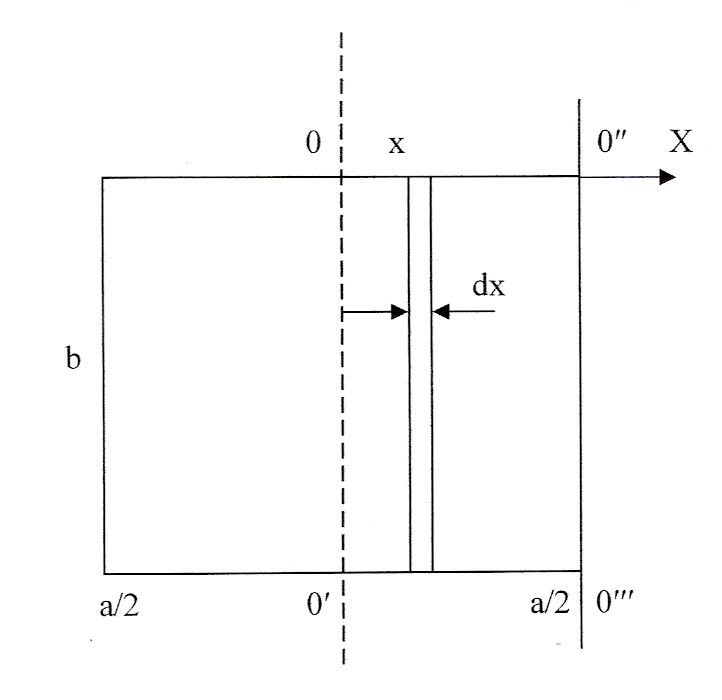
Рис. 3.1

Таким образом, момент инерции прямоугольной пластины , где масса тела Относительно оси О''О'" по теореме Штейнера получим

.

Задача 3.2. Определить ускорение центра масс сплошного цилиндра ( м), скатывающегося с наклонной плоскости без скольжения. Угол наклона , трением качения можно пренебречь. Сравнить скорости и ускорения центра масс цилиндра для случая, когда он ”сполз” с высоты без качения и когда скатился с той же высоты .

Уравнение II закона Ньютона для центра масс цилиндра в проекции на ось Х (рис. 3.2) имеет вид

.

П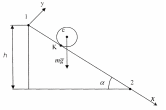 ри отсутствии силы трения ускорение центра масс м/с².

Рис. 3.2

Если цилиндр скатывается, то его движение можно свести к чистому вращению относительно мгновенной оси, проходящей вдоль линии соприкосновения цилиндра и плоскости (К) Момент инерции сплошного цилиндра относительно данной мгновенной оси по теореме Штейнера равен:

(3.16)

По основному закону динамики вращательного движения

, (3.17)

где – момент силы тяжести относительно выбранной оси (К).

Подставим (3.16) в (3.17):

и найдём угловое ускорение:

рад/с².

Тогда ускорение центра масс скатывающегося цилиндра равно: м/с², что меньше ускорения «сползающего» тела при отсутствии силы трения скольжения ( ).

Чтобы найти скорости центра масс цилиндра у основания наклонной плоскости, воспользуемся законом сохранения полной механической энергии (сила трения отсутствует). Для тела, которое соскальзывает, , а искомая скорость .

Кинетическая энергия тела, которое скатывается, складывается из энергии поступательного движения его центра масс С и энергии вращательного движения вокруг оси, проходящей через центр масс. С учётом отсутствия скольжения , получаем

.

Тогда , а

З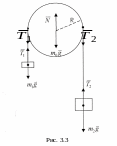 адача 3.3. На неподвижном блоке на легкой нерастяжимой нити подвешены два груза  кг и  кг. Масса блока  кг. Определить ускорение грузов и давление на ось блока. Блок считать тонким обручем.

Допустим, что блок вращается по часовой стрелке (рис. 3.3). Тогда в проекции на вертикальную ось уравнения движения грузов имеют вид

, (3.18)

. (3.19)

Уравнение блока, вращающегося относительно горизонтальной оси:

, (3.20)

где и – моменты сил натяжения нитей относительно оси вращения, с учётом (3.18) и (3.19)

, (3.21)

, (3.22)

момент инерции обруча (блока)

. (3.23)

Так как проскальзывания нити нет, то

. (3.24)

Подставляя (3.21) – (3.24) в (3.20), получаем

;

;

(м/с²).

Как видно из рисунка 3.3, сила давления на ось блока складывается из силы тяжести самого блока и сил натяжения нитей:

З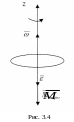 адача 3.4. Маховик, момент инерции которого  кг∙м², вращается с постоянной угловой скоростью  = 31,4 рад/с. Найти тормозящий момент М, под действием которого маховик останавливается черев t = 20 с.

Решение. Вращение происходит вокруг неподвижной оси Z, маховик тормозится силой с постоянным моментом М (рис. 3.4). Уравнение вращательного движения твердого тела (3.12):

.

Поскольку тело, вращаясь с угловой скоростью , останавливается за время t, то его угловое ускорение равно: . Тогда искомый тормозящий момент

Н∙м.

Задача 3.5. Система, состоящая из цилиндрического катка радиусом R и гири, связанных нерастяжимой и невесомой нитью, перекинутой через блок, под действием силы тяжести гири приходит в движение из состояния покоя. Определить ускорение центра инерции катка и силу натяжения Т нити. Масса цилиндра m₀, масса гири m, массой блока пренебречь. Считать, что цилиндр катится по горизонтальной поверхности без скольжения. Трением качения пренебречь.

Решение. Силы, действующие на тела, показаны на рис. 3.5. Силы и взаимно уравновешивают друг друга и дальше не рассматриваются. Силы натяжения, действующие на цилиндр и гирю , равны, поскольку массой блока и нити пренебрегаем.

Для гири напишем уравнение движения в проекции на вертикальную ось:

. (3.25)

Р ис. 3.5

Первый способ. Рассмотрим движение цилиндра как суперпозицию двух движений: вращения вокруг оси, проходящей через центр инерции С, и поступательного движения катка как целого со скоростью центра инерции.

Уравнение поступательного движения центра инерции цилиндра

, (3.26)

где – сила трения покоя, обусловленная тем, что каток катится не проскальзывая.

Вращательное движение катка вокруг оси С описывается уравнением движения вращающегося тела (3.12):

. (3.27)

Так как каток катится без скольжения, то скорость точки L должна быть равна нулю, тогда скорость центра масс , а ускорение . Далее, точка К, с одной стороны, принадлежит нити, поэтому её ускорение равно ускорению гири а (нить нерастяжима), а с другой стороны, она принадлежит цилиндру, поэтому

. (3.28)

Момент инерции катка равен:

, (3.29)

где k = 1 для полого цилиндра, – для сплошного.

Решая совместно уравнения (3.25) – (3.29), получим:

для полого цилиндра а) , б) ;

для сплошного цилиндра а) , б) .

Следует отметить, что сила трения покоя, когда каток явля-ется полым цилиндром, равна = 0, а когда сплошным – , при этом её направление противоположно указанному на рисунке.

Второй способ. Вращение тела можно рассматривать относи-тельно мгновенной оси, проходящей через точку L и совпадающей с прямой, по которой цилиндр соприкасается с поверхностью.

В таком случае нет уравнения (3.26), а уравнение движения вращающегося катка (3.27) примет вид

, (3.30)

где , – соответственно момент инерции и угловое ускорение относительно мгновенной оси.

По теореме Штейнера, для полого цилиндра,

(3.31)

Ускорение , входящее в уравнение движения гири массы (3.25), связано теперь с угловым ускорением соотношением

и . (3.32)

Решая совместно (3.25), (3.30) – (3.32), получим те же результаты, что и при решении первым способом.

З а м е ч а н и е. В данной задаче отсутствуют силы трения скольжения и качения, а в отличие от них сила трения покоя не совершает работы, связанной с убылью механической энергии. Поэтому задачу 3.5 можно решить на основе закона сохранения механической энергии.